兩類矩陣對角化問題的探討

張立華，趙琳琳，馬立新

(德州學院，山東 德州 253023)

兩類矩陣對角化問題的探討

張立華，趙琳琳，馬立新

(德州學院，山東 德州 253023)

矩陣對角化是高等代數中的重要內容，涉及到特征值、矩陣相似等基本問題，更是求解許多問題的工具。因此，就高等代數中經常遇到的一類單個矩陣對角化問題，給出一個一般結論，針對兩個矩陣同時對角化問題，給出幾個問題的證明，并且否定了一般結論的存在性，是有意義的。

高等代數；矩陣；對角化

0 引言

高等代數是現代數學的基礎,同數學分析、解析幾何構成現代數學的三大基石，是數學專業學生必修的核心基礎課。如果一個矩陣可以相似于一個對角陣，則稱該矩陣可以相似對角化，簡稱對角化[1]。矩陣對角化是高等代數中的重要內容，涉及到特征值、矩陣相似、二次型等基本問題，是高等代數教學重點之一，也是解決許多問題的必需工具[1-3]。實對稱矩陣一定可以對角化，一般的數字矩陣不一定能對角化，兩個數字矩陣還有可能同時對角化。筆者多年講授高等代數，在對單個矩陣對角化問題總結歸納的基礎上，給出了一個一般結論；對于兩個矩陣的同時對角化問題，給出了幾個問題的證明，并對一般結論的存在性進行了探討。

1 一個矩陣的對角化問題

關于一個矩陣的對角化問題，文獻[4]中給出了矩陣對角化的條件和應用，下面首先給出一個一般結論，這是文獻[4]中例3的推廣，有很多應用。

命題1 已知數域P上的n階方陣A滿足(A+mE)(A+bE)=0,其中m,b為不相等的實數，E是n階單位矩陣，證明：

(1)A的特征值只能是-m或者-b；

(2)秩(A+mE)+秩(A+bE)=n；

(3)A一定能相似對角化；

(4)若秩(A+mE)=r，則-m為A的n-r重特征值，-b為A的r重特征值；

(5)如果V1和V2分別是齊次線性方程組(A+mE)X=0和(A+bE)X=0的解空間，那么

Pn=V1⊕V2。

證 (1)設a為矩陣A的特征值，則(a+m)(a+b)為矩陣(A+mE)(A+bE)的特征值；又由于(A+mE)(A+bE)=0,而零矩陣的特征值只能為0，所以(a+m)(a+b)=0。所以a=-m或者a=-b，從而A的特征值只能是-m或者-b。

(2)由于(A+mE)(A+bE)=0,所以秩(A+mE)+秩(A+bE)≤n。又由于(A+mE)-(A+bE)=(m-b)E,而m-b≠0,從而，秩[(A+mE)-(A+bE)]=秩((m-b)E)=n≤秩(A+mE)+秩(A+bE)，所以秩(A+mE)+秩(A+bE)=n。

(3)設秩(A+mE)=r，則根據(2)，秩(A+bE)=n-r，所以齊次線性方程組(A+mE)X=0有n-r個線性無關的解，而齊次線性方程組(A+bE)X=0有r個線性無關的解；也即特征值-m有n-r個線性無關的特征向量，特征值-b有r個線性無關的特征向量；由于屬于不同特征值的特征向量是線性無關的，從而A有n個線性無關的特征向量，所以A一定能相似對角化。

(4)根據(3)的證明知道，若秩(A+mE)=r,則齊次線性方程組(A+bE)X=0有n-r個線性無關的解；從而特征值-m的重數≥n-r。同理，特征值-b的重數≥r。而特征值-m的重數+特征值-b的重數=n，所以特征值-m的重數為n-r，特征值-b的重數為r。

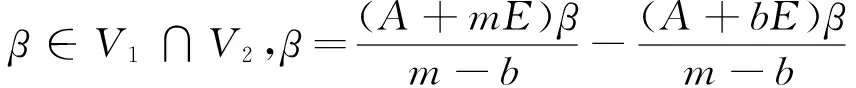
注：命題1的結論可以用來求特征值，判定矩陣是否對角化，也可確定特征子空間的維數和跟秩有關的其他問題。

例1 設n階矩陣A是冪等矩陣，證明：Tr(A)=A的秩。

2 兩個矩陣同時對角化的問題

這類題目比較難解，我們給出幾個相關問題的證明。

例2 設A、B都是n階實對稱矩陣，AB=BA，證明：存在正交矩陣Q，使Q-1AQ與Q-1BQ同時為對角矩陣。

這里Ei表示單位矩陣。因為AB=BA，所以

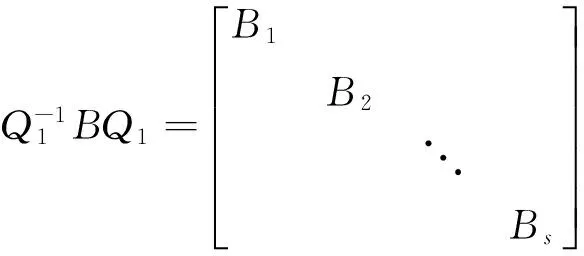
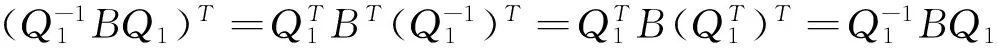
則

即Q是正交矩陣，且

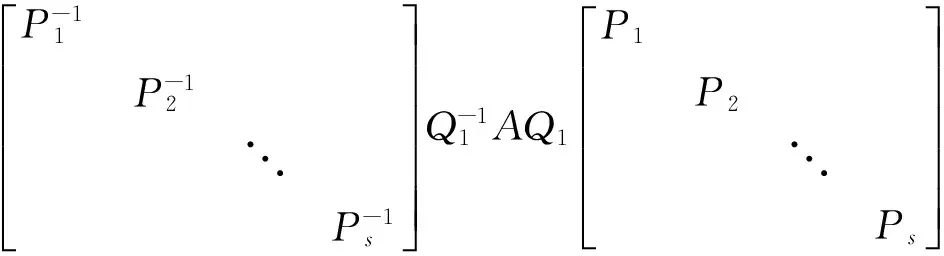
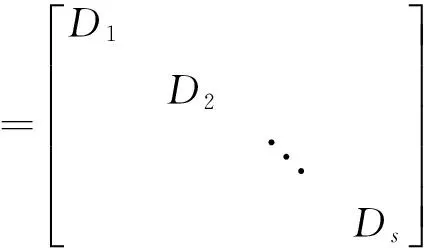
即Q-1AQ與Q-1BQ皆為對角矩陣。

例3 設A是n階實對稱矩陣，B是n階方陣，滿足B2=B,且AB=BA，證明：存在可逆矩陣Q，使Q-1AQ與Q-1BQ同時為對角形矩陣。

這里Ei表示單位矩陣。因為AB=BA，所以

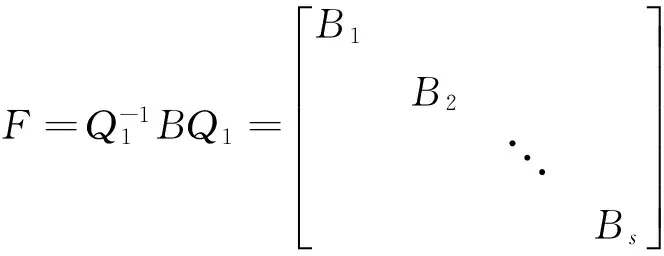
則由于Q1可逆，Pi(i=1,2,…,s)也可逆，所以Q是可逆矩陣，且

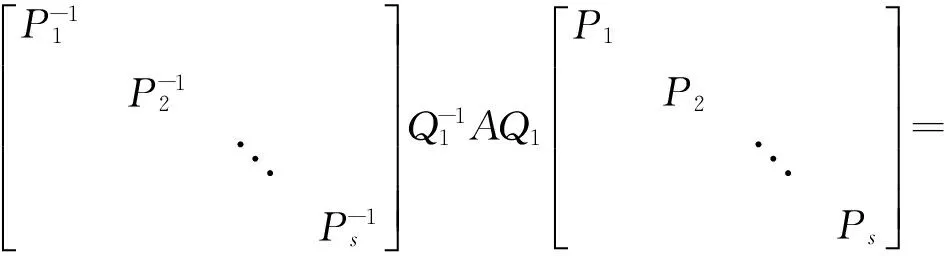
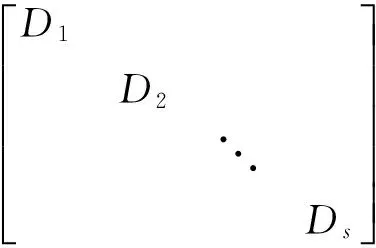
即Q-1AQ與Q-1BQ皆為對角矩陣。

例4 設A、B是兩個n階方陣，滿足A2=4E,B2=B,且AB=BA，證明：存在可逆矩陣Q，使Q-1AQ與Q-1BQ同時為對角形矩陣。

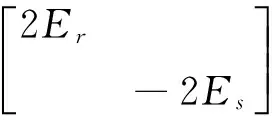
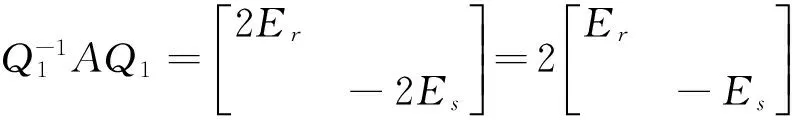
這里Er,Es表示單位矩陣。因為AB=BA，所以

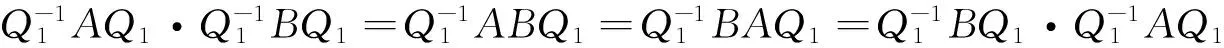
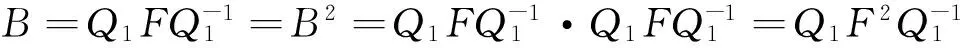
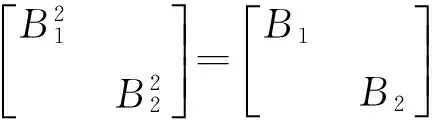
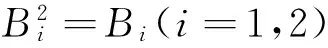
則由于Q1可逆，Pi(i=1,2)也可逆，所以Q是可逆矩陣，且

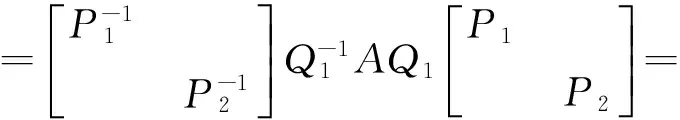
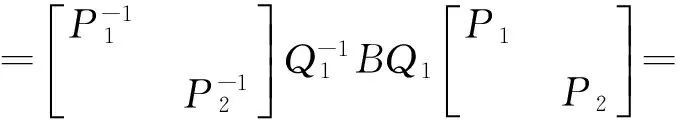
即Q-1AQ與Q-1BQ皆為對角矩陣。

例5 設A、B是兩個n階方陣，滿足A2=E,B2=E,且AB=BA，證明：存在可逆矩陣Q，使Q-1AQ與Q-1BQ同時為對角形矩陣。

例5的證明跟例4基本一樣，這里略去。例2至例5中的兩個矩陣都是可交換的，不同的是：例2中是兩個實對稱矩陣，例3中一個實對稱矩陣，一個可對角化的矩陣，例4和例5中是兩個可對角化的矩陣。受例4、例5的啟發，是不是兩個可交換、都可以對角化的矩陣就能同時對角化呢？設A、B是兩個n階方陣，A、B均可對角化，且AB=BA，則可逆矩陣Q，使Q-1AQ與Q-1BQ同時為對角形矩陣。我們經過分析否定了這一點(實際上就是按照例2至例4的思路進行證明)，或者說兩個可交換、都可以對角化的矩陣，再加上一定的條件才可以同時對角化。

3 結語

本文探討了一類單個矩陣的對角化問題，在原有工作的基礎上給出了一個一般結論。對于比較復雜的兩個矩陣同時對角化問題，我們給出了幾個問題的證明，并且得出結論：兩個可交換、都可以對角化的矩陣并不一定可以同時對角化。

[1] 王萼芳，石生明．高等代數[M].北京：高等教育出版社，2007.

[2] 楊子胥．高等代數[M].濟南：山東科學技術出版社，2001.

[3] 周明旺．關于矩陣可對角化的一個充要條件[J].通化師范學院學報，2007，28(4):10-11.

[4] 張立華.高等代數教學中關于“矩陣對角化”的一點注記[J].廊坊師范學院學報(自然科學版)，2013，13(4)：8-11.

Study on Two Classes of Diagonalization of Matrix

ZHANGLi-hua，ZHAOLin-lin，MALi-xin

(DezhouUniversity,Dezhou253023，China)

Diagonalization of matrix, which has close connection with eigenvalue, similar matrix and so on, is important content in advanced algebra and is an essential tool to solve corresponding problems. A generalized conclusion on the diagonalization of a single matrix is given. Proofs on several problems of simultaneous diagonalization of two matrices are given, and the existence of generalized conclusion on these problems is negated, which proves to be of importance.

advanced algebra；matrix；diagonalization

2016-01-05

山東省自然科學基金資助項目(ZR2013AQ005)

張立華(1981-),女，理學博士,德州學院數學科學學院副教授，研究方向：孤立子與可積系統。

O151.21

A

1674-3229(2017)01-0005-04