巧用數理結合法 妙解一道競賽題
張義勇 徐翊軒
(1. 江蘇省常州外國語學校物理組,江蘇 常州 213000;
2. 江蘇省常州外國語學校2017屆6班,江蘇 常州 213000)
巧用數理結合法 妙解一道競賽題
張義勇1徐翊軒2
(1. 江蘇省常州外國語學校物理組,江蘇 常州 213000;
2. 江蘇省常州外國語學校2017屆6班,江蘇 常州 213000)
筷子搭碗是典型的初中物理競賽題,普遍出現在各種教輔書和高中自主招生試題中.本文所舉的例題,常見解法要用到高中知識,超出了初中生的能力范疇.筆者先后構建物理模型和數學模型,通過數理結合,在初中知識的框架內解決問題,能有效激發學生的學習興趣,體現初中物理競賽的內涵和品質.
數理結合;物理競賽;案例分析
1 原題
如圖1所示,直徑為36cm的半球形碗固定在水平面上,碗的端口水平.一根密度分布均勻、長度為47cm的光滑桿ABC擱置在半球碗上,碗的厚度不計,桿平衡時碗內部分AB段與碗外部分BC段的長度之比為( ).
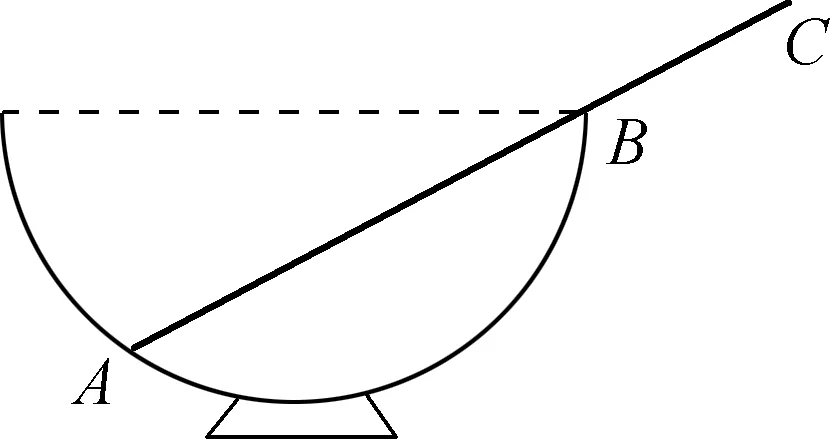
圖1
A. 38∶9 B. 35∶12
C. 32∶15 D. 27∶20
2 原解法
讀者可以上網搜索答案,這里不再贅述.但此解法中要用到“沿筷子方向的受力平衡”,即利用高中物理的“力的分解”來分析問題.由于初中學生沒有相關的知識儲備,在理解上會遇到很大的困難.
3 數理結合法
如圖2所示,由于支持力與接觸面垂直,A點受到的支持力F1指向O點,B點受到的支持力F2與AB垂直,則F1、F2的延長線一定相交,將其交點命名為F.
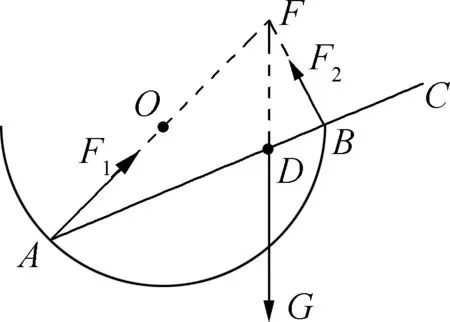
圖2
3.1 靈活選取支點,建立杠桿模型
常見的杠桿分析法以A或B為支點,列杠桿平衡式.本方法另辟蹊徑,以F點為支點,則F1、F2的力臂都是零.由于筷子靜止,整體平衡,則重力G的力臂也一定為零,即點F一定在重力G的反向延長線上.
3.2 結合圓的知識,構建幾何模型
如圖3所示,畫出水平的直徑BG,連接AG,將BG與DF的交點命名為H.由圓周角的知識可知∠GAB=∠FBA=90°,且OA=OB,則△AOB為等腰三角形,可得∠OAB=∠OBA.再由AB為△GAB和△FBA的共同底邊,可得△GAB≌△FBA,利用三角形全等關系,可得AF=BG=36cm.
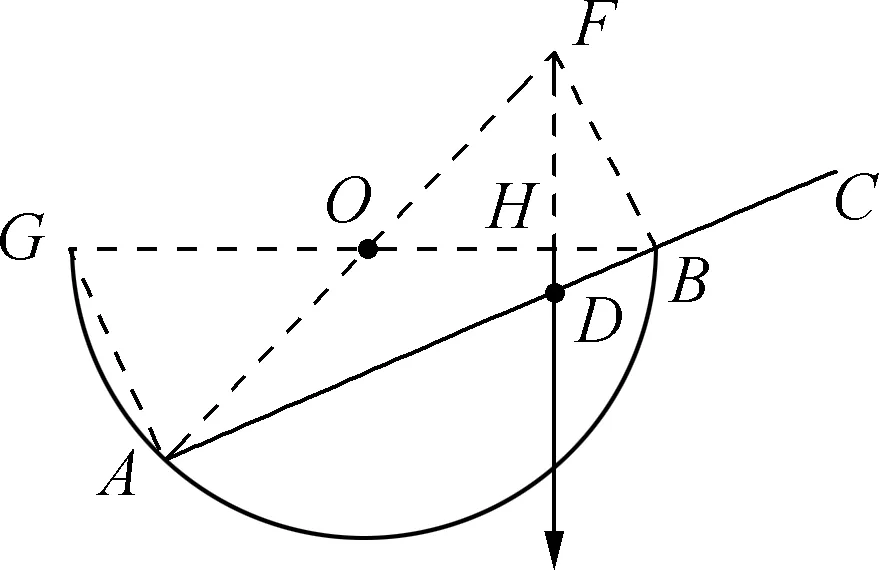
圖3
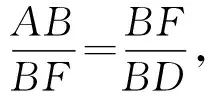
3.3 利用勾股定理,構建一元二次方程
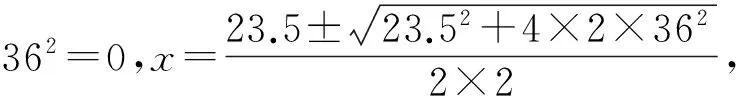
4 總結
本方法應用了初中物理和數學的知識,沒有超出要求.解法的重點在于靈活選取杠桿的支點,構建三個力的力臂均為零的杠桿模型,巧妙結合圓的知識,構建三角形相似和全等,再利用勾股定理和一元二次方程解決問題.
在本案例中,需要學生跨學科調用初中知識,通過數理結合的方法來解決問題,既能體現競賽題的內涵與魅力,又能培養學生的學科融合能力,提升學生的綜合素養.

