懸索橋鋼桁梁斷面質量慣性矩簡化計算方法

華旭剛+楊坤+溫青+陳政清

摘 要：魚骨單主梁模型是分析大跨度鋼桁梁懸索橋抗風性能的常用簡化模型.針對由于懸索橋鋼桁梁斷面桿件眾多造成的其扭轉質量慣性矩計算繁瑣、精度低的問題，提出一種基于均勻附加扭轉質量慣性矩前后結構扭轉頻率的變化計算鋼桁梁扭轉質量慣性矩的方法，并給出了該方法的理論說明、適用條件等.以一鋼桁梁懸臂結構為例進行了數值仿真，結果表明：附加扭轉質量慣性矩施加在全截面或上、下弦桿節點，且鋼桁梁的長細比L/D≥20時，該方法計算的扭轉質量慣性矩有較高的精度.采用該方法計算了多座鋼桁梁懸索橋的主梁扭轉質量慣性矩，比較了全桁架模型和單主梁模型扭轉振動頻率，驗證了方法的有效性.

關鍵詞：鋼桁梁；懸索橋；扭轉質量慣性矩；抗風設計

中圖分類號：U448.25 文獻標志碼：A

文章編號：1674-2974（2017）03-0001-07DOI：10.16339/j.cnki.hdxbzkb.2017.03.001

Abstract：The simplified “fish-bone” model is commonly employed for the analysis of wind-induced responses of truss-stiffened suspension bridges， and one key step in establishing such a model is the calculation of the mass moment of inertia for the stiffening truss. Due to numerous members in a stiffening truss section， the calculation process of the moment of inertia is usually complicated and imprecise. Therefore， a new method is proposed based on the change in torsional frequencies of a cantilever truss girder caused by attaching the additional mass moment of inertia on the truss nodes， where the theoretical background is given， and the applicable conditions are also investigated. By taking a cantilever truss girder as an example， numerical simulation results show that the proposed method provides the best accuracy when the known mass moment of inertia is uniformly applied to all section nodes or to the nodes of chord joints， and the slenderness ratio of truss girder exceeds 20. Finally， the mass moments of inertia of stiffening truss are obtained by the proposed method， and are then used to establish the simplified “fish-bone” models for several selected suspension bridges. The torsional frequencies obtained by the simplified “fish-bone” models agree well with those predicted by their detailed models， which validates the effectiveness of this simplified method.

Key words：stiffening truss； suspension bridges； mass moment of inertia； wind-resistant design

鋼桁梁具有剛度大、用鋼量省、適應雙層橋面、抗風性能良好等優點，在國內外大跨度懸索橋中得到廣泛應用，如香港青馬大橋[1]、美國的金門大橋[2]、日本的明石海峽大橋[3]等.在鋼桁架為主梁的懸索橋的主梁節段模型試驗中，通常采用節段模型測力法獲得鋼桁梁斷面的靜三分力或顫振導數.為與節段模型測力法相適應，需要建立鋼桁梁的等效單主梁模型.鋼桁梁斷面的扭轉質量慣性矩是建立等效單主梁模型的一個重要參數，其計算的精確與否將直接影響等效單主梁模型的扭轉頻率、振型等參數，因此，如何快捷、有效地計算鋼桁梁的扭轉質量慣性矩顯得尤為重要.

鋼桁梁通常由數量眾多的薄壁工字型或箱型截面構件構成，由上下弦桿、腹桿、平縱聯及橫聯等組成.沿橋跨方向，由于不同位置處的橫斷面的差異性，造成其質心沿橋跨方向也在不斷變化，故很難精確計算鋼桁梁的扭轉質量慣性矩.常規方法是找到節點處橫斷面的質心位置，并假定沿橋跨方向各橫斷面質心位置不變，然后計算鋼桁梁的扭轉質量慣性矩，并以此作為單主梁模型扭轉質量慣性矩的初值，不斷調整單主梁模型中此參數，來使全桁架模型與單主梁模型中的扭轉頻率一致[4].這種方法缺乏理論基礎，主觀性大，且計算繁瑣.于永帥[5]提出一種簡化算法：通過在鋼桁梁上沿橋跨方向均勻附加扭轉質量慣性矩，利用附加質量慣性矩前后2次動力特性的變化反算鋼桁梁自身扭轉質量慣性矩.這種方法思路清晰，計算便捷，但其對此方法的理論證明、適用條件、附加扭轉質量慣性矩的施加位置等未作詳細研究.

基于此，本文對該方法作進一步研究.首先，闡述了懸索橋風振分析所用有限元模型的特征，說明了計算扭轉質量慣性矩的重要性和必要性；然后，詳細地討論了本文提出的鋼桁梁斷面扭轉質量慣性矩的計算方法，并給出了該方法的理論說明和適用條件；接著，通過數值仿真，分析了鋼桁梁的長細比、附加扭轉質量慣性矩的施加位置對計算結果的影響；最后，應用該方法計算了多座鋼桁梁懸索橋的主梁等效扭轉質量矩，并驗證了結果的可靠性.

1 懸索橋動力分析模型

隨著現代大跨橋梁的日漸輕柔化，懸索橋及斜拉橋的抗風抗震性能越來越受到人們的關注，這方面的研究必須借助三維有限元分析方法[6].我們可以采用由多種單元（包括梁單元、板單元、殼單元等）組合的有限元方法對懸索橋進行分析，但這種方法必會涉及大量的運算，當采用時域法進行隨機動力分析時，為了得到大量樣本的統計結果，這個問題顯得尤為突出，且往往是行不通的[7].為此，必須將結構的剛度、質量、邊界條件等根據一定的等效原則對結構進行一定的抽象和簡化，建立實用的動力分析模型.目前常用的簡化模型有單主梁、雙主梁、三主梁模型以及實體塊或板殼單元模型[7-9].

單主梁模型把橋面系的剛度（豎向、橫向撓曲剛度、扭轉剛度）和質量（平動質量和轉動慣量）都集中在中間節點上，節點和吊桿之間采用剛臂連接或處理為主從關系.單主梁模型適用于自由扭轉剛度較大的閉口截面主梁.這種模型的優點是主梁的剛度和質量模擬較為準確，且計算量小；缺點是橫梁的剛度和主梁的翹曲剛度未能得到充分考慮.

雙主梁模型將主梁的豎向剛度平均分配給2根邊主梁以保證豎向剛度的等效，可近似地考慮主梁約束扭轉的貢獻，適合于開口或半閉口截面的主梁，缺點是對側向剛度和約束扭轉剛度的模擬不準確.

三主梁模型是目前較完善的一種橋面系模型，它通過適當的剛度和質量分配來滿足等效原則，可以克服上述2種模型的缺點，但使用三主梁模型會使結構離散的單元數大大增加，這對于抗風計算的時域分析的求解效率是十分不利的.

實體塊或板殼單元模型中，主梁采用體板單元模擬，能較準確地計算結構整體和局部的變形和內力.其缺點是計算量相當大，對計算機硬件的要求比較高[10].

鋼桁梁具有較大的扭轉剛度，且考慮到后續風振響應分析、氣彈模型的設計，需要采用單主梁計算模式模擬鋼桁架結構.

2 扭轉質量慣性矩

2.1 扭轉質量慣性矩的定義

扭轉質量慣性矩，簡稱質量慣性矩或質量矩，又叫轉動慣量，是剛體動力學中的一個重要概念，它表征物體轉動慣性的大小.為敘述方便，下文均采用質量矩.

質量矩為空間中質量關于距離的二次矩.對于離散體系，它對空間任意一條直線z的質量矩定義為：

2.2 簡化算法

2.2.1 計算原理

本文提出的是一種基于均勻附加質量矩前后結構動力特性的變化計算鋼桁梁質量矩的方法.該方法采用質量矩均勻分布的懸臂梁模型，通過在鋼桁梁上沿橋跨方向均勻附加質量矩，然后根據附加質量矩前后懸臂梁扭轉頻率的變化反算鋼桁梁自身的質量矩，下面對該理論進行詳細說明.

2.2.2 理論證明

為下文證明方便，限制懸臂梁模型的平動自由度，并將其離散化為只有扭轉自由度的N自由度體系，如圖2所示.

式中：φ1為第一階扭轉振型； K為N階剛度方陣； M為N階質量方陣； k1和m1分別是第一階模態剛度和模態質量.由于模態振型φr為任意尺度的無量綱特征向量，不同的模態振型尺度，模態質量mr和模態剛度k1不同，因此通常需要對振型進行規格化，常用的振型規格化方法有2種[11]：1）按質量歸一化的振型規格化，即結構的模態質量為mr=1；2）特定自由度幅值取1的振型規格化，即某個自由度的幅值取1，并以這個指定的值為基準確定其他自由度幅值，如指定最大自由度幅值為1.本文采用指定最大自由度幅值為1的方法對振型進行規格化.

在每個節段上均附加大小為ΔIm的質量矩，前面已經證明了質量矩均勻分布的懸臂梁模型附加質量矩前后，結構的扭轉振型不變，因此扭轉基頻變為ω1*，

式中：Im表示鋼桁梁各節段質量矩大小；ΔIm表示鋼桁梁各節段附加的質量矩大小；ω1，ω1*分別表示質量矩附加前后的懸臂鋼桁梁的一階扭轉圓頻率；f1，f1*分別表示質量矩附加前后的懸臂鋼桁梁的一階扭轉頻率.

公式（12）就是計算質量矩的依據.為方便使用，現將該方法計算步驟概括如下：

1）建立適當長度的鋼桁梁有限元模型，使其處于懸臂狀態，計算一階扭轉頻率f1；

2）沿梁跨方向在鋼桁梁模型上各節段處附加質量矩大小均為ΔIm的扭轉質量單元，并計算一階扭轉頻率f1*；

3）利用公式（12）計算鋼桁梁各節段的扭轉質量慣性矩Im.

2.2.3 適用條件

由證明過程知，結構的質量矩需要滿足其沿梁跨均勻分布，且沿梁跨方向在各節段施加的附加質量矩大小相同.

3 數值仿真分析

為了驗證簡化算法的可行性和計算結果的精確性，通過ANSYS對影響鋼桁梁質量矩計算結果的因素進行分析.

3.1 有限元模型

主梁采用板桁結合型鋼桁加勁梁，主桁架為帶豎腹桿的華倫式結構，由上弦桿、下弦桿、豎腹桿和斜腹桿組成.主桁桁高9 m，桁寬35.4 m，節間長度8.4 m.在主桁架每個節點處設置一道主橫桁架，下平聯采用K形體系，節點處橫斷面如圖3所示.

建立有限元模型時，上下弦桿、腹桿、平縱聯、橫梁等采用beam188單元，橋面板采用shell63單元.為驗證該方法所計算結果的正確性，兩者的密度均取為0，兩者的扭轉質量慣性矩通過mass21單元施加，各節段（節段長度為8.4 m）質量矩Im均取為4.028×107 kg·m2，具體到各節點的質量矩大小見表1（考慮到橋面板的影響，故頂層節點的質量矩較大）.建立加勁梁有限元模型如圖4所示，后處理時質量矩陣采用集中質量矩陣.

3.2 影響因素

鋼桁梁質量矩計算結果的主要影響因素有2個，一是鋼桁梁的長細比L/D（L表示鋼桁梁的長度，D表示鋼桁梁寬度和高度的較大值），二是附加質量矩的施加位置.

1）鋼桁梁的長細比： 鋼桁梁為組合結構，從單一桿件分析，各桿件受力以軸力為主，可近似看成二力桿；但從整體來看，主桁上、下弦桿以及平、縱聯在適當間距內提供了桁架承受較大彎矩的能力；橫梁和上下平聯連接2片主桁能夠提供整體抗扭剛度.當鋼桁梁長度遠大于梁寬度和梁高度時，桁架結構成為一個具有明顯梁特性的單梁[4].

為研究鋼桁梁的長細比對質量矩計算結果的影響，選取長細比分別為L/D≈10（L=352.8 m），20（L=740 m）和55（L=1 933.6 m）的3個鋼桁梁進行計算.

2）附加質量矩施加位置：桁架橫斷面有多個節點，在不同節點處附加質量矩對計算結果可能會產生影響.原桁架橫斷面左右對稱，故附加質量矩應左右對稱施加，在不同位置處附加質量矩時的工況見表2.

3.3 計算結果

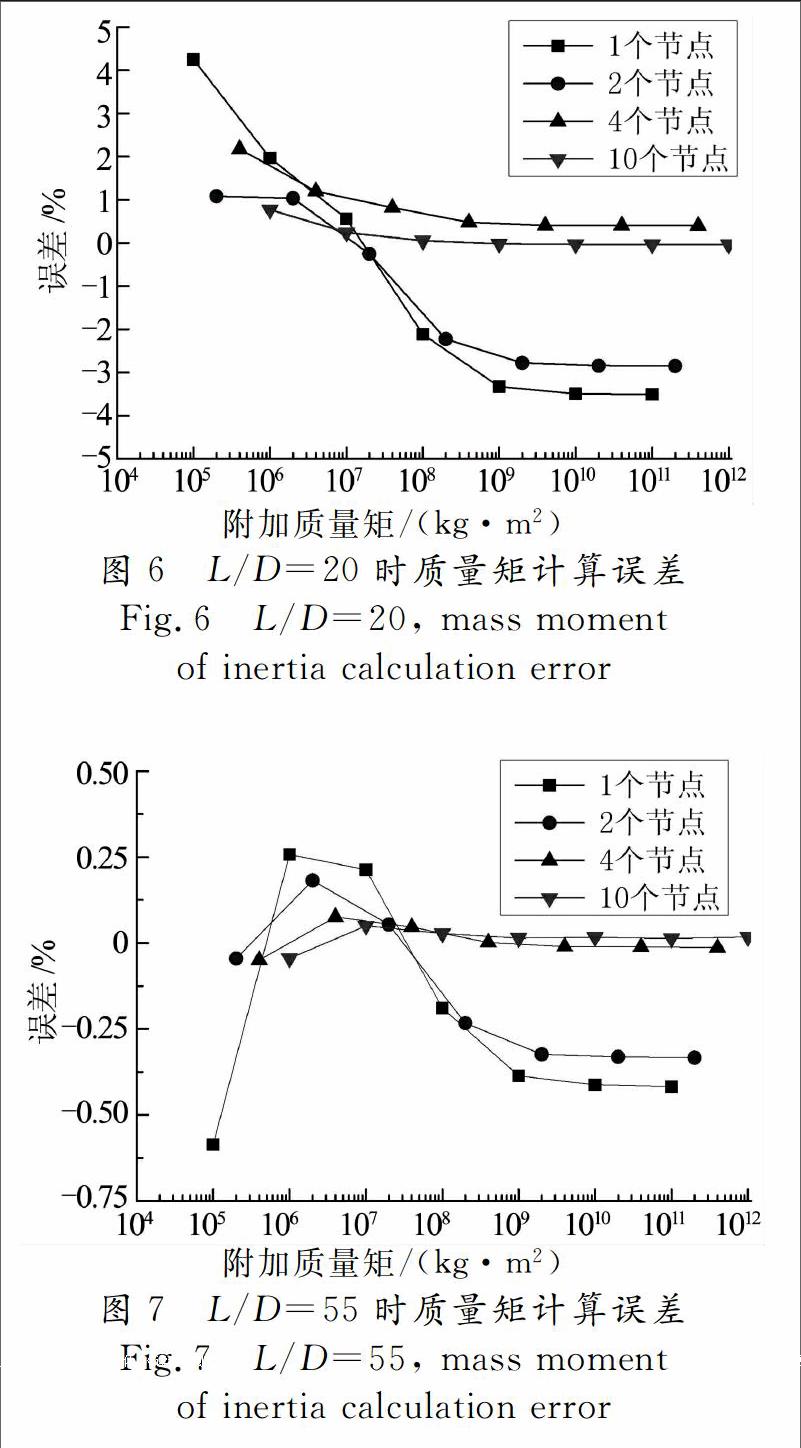
利用簡化算法可以得到鋼桁梁的質量矩（稱為計算值），將計算值與真實值（見表1）作比較，得到計算誤差，如圖5—圖7所示.鋼桁梁取不同長細比時，用簡化算法計算其質量矩過程相似，所以僅給出了L/D=10時工況一的計算步驟，見表3.這里，ΔIm表示鋼桁梁各節段的附加質量矩大小，fi表示懸臂鋼桁梁的一階扭轉頻率，Im表示鋼桁梁各節段的質量矩大小.為保證計算結果的穩定性，計算時選取了不同大小的附加質量矩.

由圖5-圖7可知：

1）就鋼桁梁的長細比L/D而言，隨著長細比的增加，質量矩計算誤差減小.當L/D=20，附加質量矩采用4節點或10節點加載時，質量矩計算誤差在3%以內；當L/D=55，附加質量矩采用4節點或10節點加載時，質量矩計算誤差在0.1%以內.

2）就附加質量矩施加位置而言，4節點、10節點加載與1節點、2節點加載相比，質量矩計算誤差更小，即上下弦桿加載或全截面加載時，質量矩計算誤差更小.

下面從力學角度對以上2種因素進行簡要分析.在簡化算法的推導過程中，得到一個結論：質量矩均勻分布的懸臂梁模型在附加質量矩前后，結構的一階扭轉振型不變.然而對于鋼桁梁懸臂結構，這個結論很難嚴格成立.

當懸臂鋼桁梁長細比較小時（L/D=10），無論附加質量矩在何處加載，質量矩計算誤差均較大.原因是懸臂鋼桁梁的長細比較小，其在扭轉時會發生翹曲，造成同一橫截面各節點扭轉角有明顯差異，平截面假定不再滿足，故附加質量矩前后，很難保證它的一階扭轉振型嚴格不變.

未附加質量矩時，懸臂鋼桁梁的剛度、質量分布較合理，其一階扭轉振型為桁架斷面整體的扭轉變形，不會發生局部變形.附加質量矩后，結構剛度不變，質量分布發生變化.對于工況一和工況二，附加質量矩施加的位置處剛度比較小，可能導致結構一階扭轉時發生局部變形，從而造成較大的計算誤差.對于工況三，附加質量矩施加的位置處剛度比較大，結構一階扭轉振型沒有局部變形.對于工況四，橫斷面各節點均附加質量矩，同一斷面內質量分布均勻變化，結構的一階扭轉振型沒有局部變形.

3.4 一階扭轉頻率對比

理論上，若懸臂鋼桁梁與懸臂單主梁滿足剛度、質量（矩）、邊界條件等效，則兩者的頻率等動力特性參數應該基本相同.

這里，鋼桁梁長細比取L/D=55，附加質量矩采用全截面加載.建立懸臂單主梁模型時，各節段（節段長度為8.4 m）質量矩大小仍取為4.028×107 kg·m2，計算得到鋼桁梁豎向、側向的慣性矩分別為11.8 m4和230 m4，扭轉慣性矩為11.1 m4，計算不同的附加質量矩下懸臂鋼桁梁和懸臂單主梁的一階扭轉頻率，計算結果見表4.這里，ΔIm表示鋼桁梁各節段的附加質量矩大小，f桁表示懸臂鋼桁梁的一階扭轉頻率，f單表示懸臂單主梁的一階扭轉頻率.

需要說明的是，第一，質量矩只影響扭轉有關頻率及振型，因此實際建模時，不需要沿梁長限制各節段的豎向和側向自由度，只需找到懸臂梁的一階扭轉頻率.第二，附加質量矩不可太小或太大，若太小，附加質量矩前后結構頻率變化甚微，則公式（12）可能會造成較大的計算誤差；若太大，則可能導致質量矩陣出現畸變，從而難以求解特征值.

4 工程應用實例

常見的大跨度懸索橋的鋼桁梁，各桿件截面沿梁跨變化不大，其質量分布沿梁長可近似看作均勻分布，滿足該方法的適用條件.本文以洞庭湖二橋和矮寨大橋為例，來驗證該方法的有效性.

洞庭湖二橋為主跨為1 480 m的雙塔雙跨鋼桁架懸索橋，橋跨布置為（1 480+453.6） m，主梁全長為1 933.6 m.主橋主纜的孔徑布置為（460+ 1480+491） m，主纜垂垮比F/L=1/10，主索中心距為35.4 m，采用平面索布置.主梁是鋼桁梁，其有關信息與上面數值仿真分析中的鋼桁梁相同；主塔為門式框架橋塔，兩岸錨碇為重力式錨碇.矮寨大橋為主跨為1 176 m的單跨鋼桁架懸索橋，有關該橋的詳細信息可參見文獻[12]，這里不再詳述.

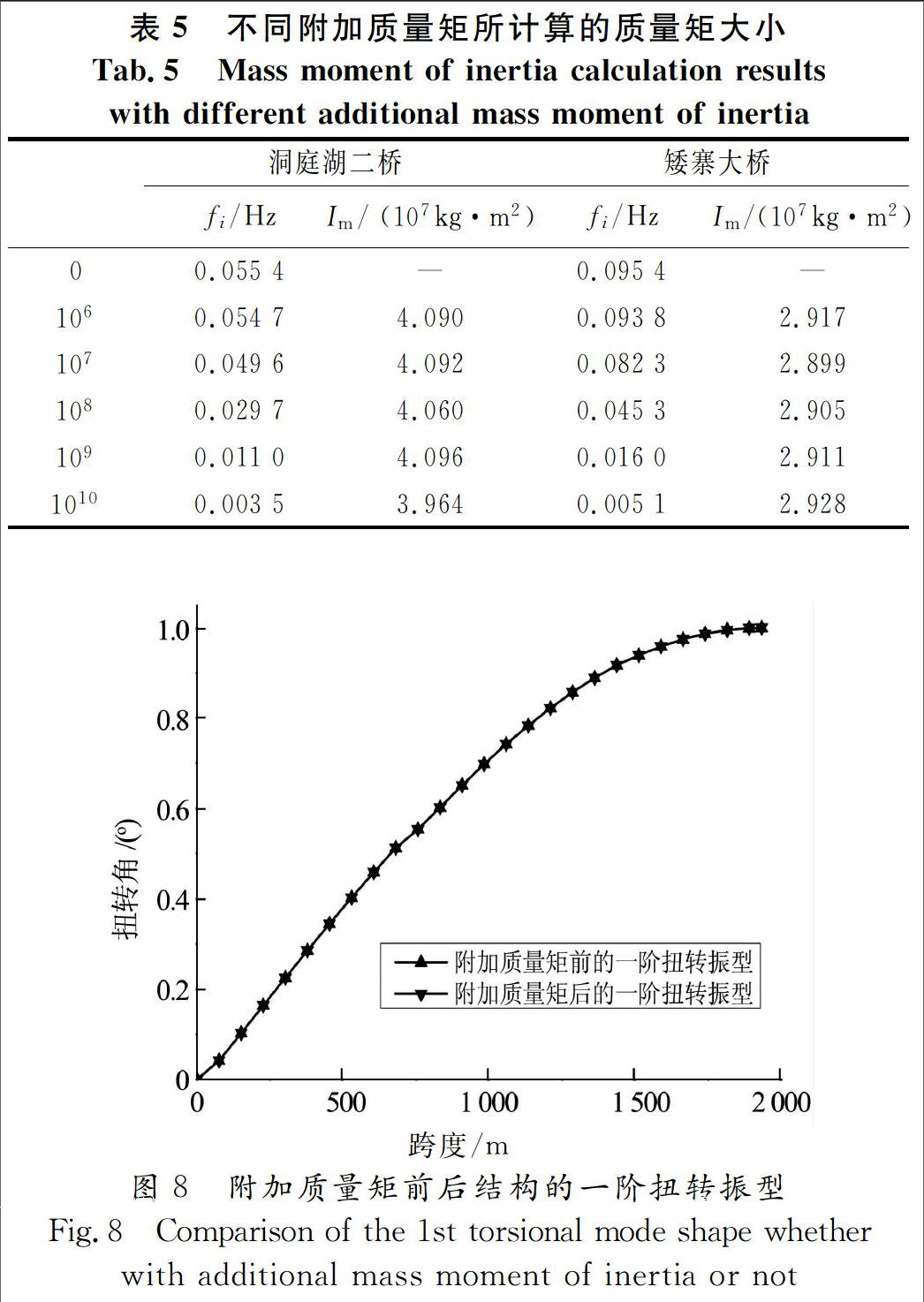
計算鋼桁梁質量矩時，為減小計算誤差，采用全截面加載，懸臂梁跨度取原橋主梁全長，所使用單元類型與上文數值仿真分析中相同.所不同的是鋼桁架各桿件及橋面板的質量矩不再采用mass21單元施加，而是按實際密度加以考慮，計算結果見表5.這里，ΔIm表示節間長度的桁梁所附加質量矩大小（洞庭湖二橋主梁、矮寨大橋主梁的節間長度分別為8.4 m，7.25 m），fi表示懸臂鋼桁梁的一階扭轉頻率，Im表示節間長度的鋼桁梁質量矩大小.需要說明的是，這里已驗證了附加質量矩前后，懸臂鋼桁梁的一階扭轉振型未發生改變.這里給出了洞庭湖二橋加勁梁的懸臂梁模型在附加質量矩前后的一階扭轉振型圖（圖8）.

理論上，懸索橋的全桁架模型和單主梁模型兩者計算的結構動力特性基本上是一樣的.為驗證該方法計算得到的質量矩的正確性，單主梁模型中的質量矩參數采用該方法計算得到的數值，計算扭轉相關頻率，并與全桁架模型的計算結果對比，見表6.由表6知，本文方法計算得到的質量矩準確度高.

5 結 論

本文討論了一種基于附加質量矩前后結構動力特性的變化計算鋼桁梁質量矩的方法.

數值仿真結果表明：1）鋼桁梁的長細比L/D對質量矩的計算有較顯著的影響，L/D≥20時，該方法計算的質量矩有較高的精度.對于鋼桁梁簡支梁，其長細比L/D一般小于20，故此方法對計算鋼桁梁簡支梁的質量矩有局限性.2）附加質量矩的施加位置對質量矩的計算結果有較顯著影響，當附加質量矩均勻附加在全截面或上、下弦桿時計算精度更高.此外，附加質量矩時，沿梁跨方向，要保證在鋼桁梁各節段處均勻附加扭轉質量單元；沿橫斷面方向，要保證附加扭轉質量單元左右對稱分布.

采用該方法分別得到了洞庭湖二橋和矮寨大橋加勁梁的質量矩，并將該參數應用到單主梁模型中，計算了洞庭湖二橋的動力特性，并與全桁架模型的計算結果進行了對比.結果表明，兩者扭轉相關頻率基本相等，驗證了該方法的有效性.

參考文獻

[1] 劉正光.香港青馬大橋的設計[J].土木工程學報，1992，25（5）：77-80.

LIU Zhengguang. The design of Qingma Bridges in HongKong[J]. China Civil Engineering Journal， 1992，25（5）：77-80.（In Chinese）

[2] TANAKA H ， DAVENPORT A G. Wind-induced response of Golden Gate Bridge[J]. Journal of Engineering Mechanics， 1983，109（1）： 296-312.

[3] KITAGAWA M. Technology of the Akashi Strait Bridge [J]. Structural Control and Health Monitoring， 2004，11（2）：75-90.

[4] 胡峰強.山區風特性參數及鋼桁架懸索橋顫振穩定性研究[D].上海：同濟大學土木工程學院，2006：68-90.

HU Fengqiang. The research of wind characteristic parameters and flutter instability of suspension bridges with a steel truss stiffened girder in mountainous regions[D]. Shanghai： College of Civil Engineering， Tongji University， 2006：68-90. （In Chinese）

[5] 于永帥.鋼桁架懸索橋抖振響應及其影響參數分析[D].長沙：湖南大學土木工程學院，2011：14-20.

YU Yongshuai. Buffeting response of steel truss girder suspension bridge and influence parameters investigation[D]. Changsha： College of Civil Engineering， Hunan University， 2011：14-20. （In Chinese）

[6] NAMINI A， ALBRECHT P， BOSCH H. Finite element-based flutter analysis of cable-suspended bridges[J]. Journal of Structural Engineering， 1992， 118（6）：1509-1525.

[7] 蘇成.大跨度斜拉橋三維有限元動力模型的建立[J].華南理工大學學報，1999，27（11）：51-56.

SU Cheng. The established 3-D element finite dynamic models for long-span cable-stayed bridges[J]. Journal of South China University of Technology， 1999，27（11）：51-56.（In Chinese）

[8] 劉志文，洪涵，梁立農，等. 廣東江順大橋的抗風性能試驗研究[J]. 湖南大學學報：自然科學版，2015，42（3）： 112-119.

LIU Zhiwen， HONG Han， LIANG Linong， et al. Experimental investigation of wind-resistant performance of Jiangshun Bridge in Guangdong [J]. Journal of Hunan University： Natural Sciences， 2015， 42（3）： 112-119.（In Chinese）

[9] 范立礎.橋梁抗震[M].上海：同濟大學出版社，1997：118-121.

FAN Lichu. Aseismic of bridges[M]. Shanghai： Tongji University Press， 1997：118-121. （In Chinese）

[10]王浩，李愛群，郭彤，等.帶中央扣的超大跨度懸索橋多尺度有限元模擬方法[J].中國公路學報，2009，22（6）：60-66.

WANG Hao， LI Aiqun， GUO Tong， et al. Multi-scale finite element modeling method on super-long-span suspension bridges with central bucle[J]. China Journal of Highway and Transport， 2009， 22（6）： 60-66.（In Chinese）

[11]R W 克拉夫.結構動力學[M].北京：高等教育出版社，1997：160-171.

CLOUGH R W.Structural dynamics[M].Beijing： Higher Education Press，1997：160-171. （In Chinese）

[12]HU Jianhua， CUI Jianfeng. Innovative techniques of design of Aizhai Bridge in West Hunan[J]. Bridge Construction， 2011，31（6）：54-61.