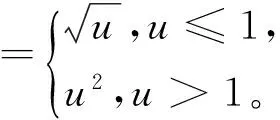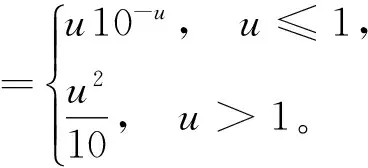一類彈性梁方程正解的存在性
鞠夢蘭,王文霞,郝彩云
(太原師范學院數(shù)學系,山西晉中 030619)
一類彈性梁方程正解的存在性
鞠夢蘭,王文霞,郝彩云
(太原師范學院數(shù)學系,山西晉中 030619)
彈性梁是彈力力學和工程物理中一種比較常見的數(shù)學模型,為了將此模型更準確地應用于工程領域中,在對一端固定,一端滑動支撐的彈性梁方程研究的基礎上,研究了此類彈性梁方程的多解性。通過將此類邊值問題轉化為積分方程后,進而等價于算子的不動點問題,結合其Green函數(shù)的性質與Guo-Krasnoselskii錐拉伸與壓縮不動點定理,討論了此類彈性梁方程正解的存在性問題。在非線性項滿足適當條件下建立參數(shù)的取值范圍,獲得了此類邊值問題至少有1個正解,2個正解的存在性結果與正解的不存在性結果。結論上獲得了關于此類問題至少有1個正解,2個正解及沒有正解的存在的特征值區(qū)間。研究結果有助于彈性梁的穩(wěn)定性分析,豐富了材料力學的相關理論。
非線性泛函分析;彈性梁;正解;Guo-Krasnoselskii不動點定理;材料力學
考察邊值問題:
(1)
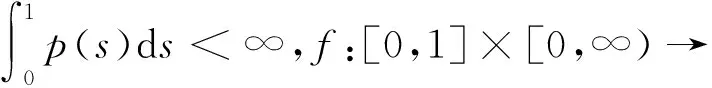
不同的梁方程可以通過不同邊界條件的四階邊值問題來刻畫,由于梁方程的實際背景及意義,近年來對四階邊值問題的研究很活躍,尤其是對兩端簡單支撐與兩端固定的梁方程(即邊界條件為u(0)=u(1)=u″(0)=u″(1)和u(0)=u(1)=u′(0)=u′(1)=0)的研究,并且取得了豐碩的研究成果[1-11];也有不少研究者致力于對懸臂梁方程(即邊界條件為u(0)=u′(0)=u″(1)=u?(1)=0)的研究[12-13]。目前對一端固定,一端滑動支撐的梁方程(即本文所討論情形)的討論還比較少見。陸海霞等[14]應用錐理論和不動點指數(shù)方法研究了此類梁方程至少有1個正解的存在性問題。 受此啟發(fā),文獻[15]研究了此類梁方程的特征值問題,獲得了至少有1個正解存在的特征區(qū)間。但是此類問題的多解性研究尚不多見,通過對三階邊值問題多解性文獻的研讀發(fā)現(xiàn)[16-19],研究者們通常利用Guo-Krasnoselskii錐拉伸與壓縮不動點定理,單調迭代技術去討論這類問題的多解性問題。本文主要通過建立適當?shù)腻F,利用錐上的Guo-Krasnoselskii錐拉伸與壓縮不動點定理,建立了特征值問題(1)至少有1個,2個及沒有正解的存在的特征區(qū)間。
1 預備和記號
引理1 設
(2)
則G(t,s)是邊值問題:
(3)
的格林函數(shù)。
引理2[15]1)G(t,s)≥0,(t,s)∈[0,1]×[0,1];
2)G(t,s)>0,(t,s)∈(0,1)×(0,1);
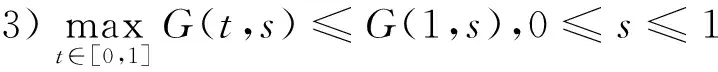
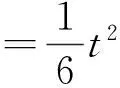
下面給出一些記號:
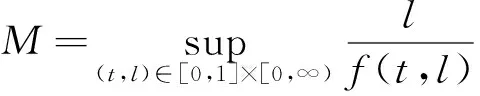
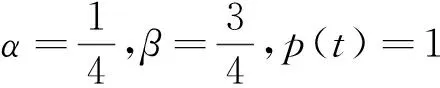
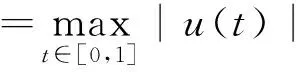
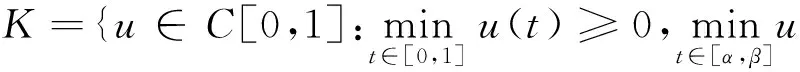
Kc={u∈K,‖u‖≤c}, ?Kc={u∈K,‖u‖=c},
引理3Tλ是K→K全連續(xù)算子。
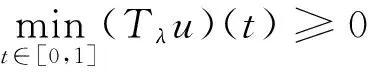
另一方面,
τ‖Tλu‖,
即Tλ(K)?K,由f與p的連續(xù)性易得Tλ的連續(xù)性。
下證Tλ是緊的。
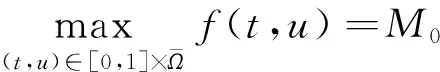
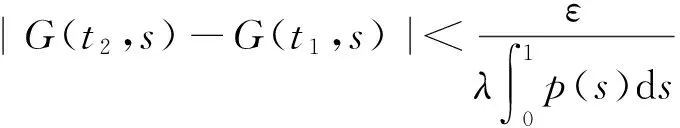
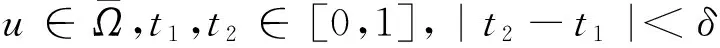
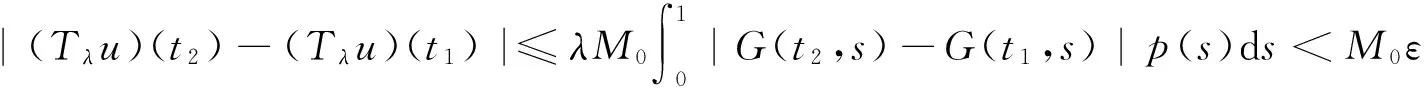
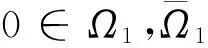
1)‖Tu‖≤‖u‖,u∈K∩?Ω1且‖Tu‖≥‖u‖,u∈K∩?Ω2;
2)‖Tu‖≥‖u‖,u∈K∩?Ω1且‖Tu‖≤‖u‖,u∈K∩?Ω2;
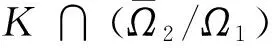
引理4 設存在c1,c2>0,且c1≠c2,使得:
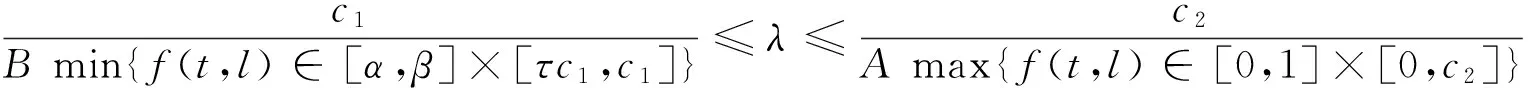
(4)
則BVP(1)至少有1個正解。
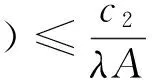
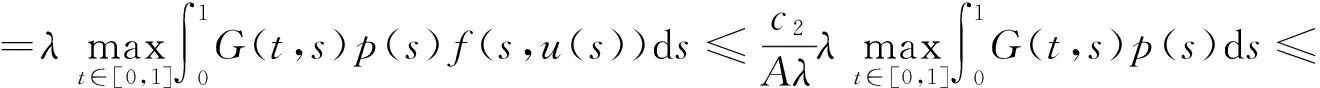
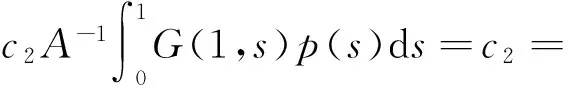
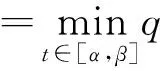
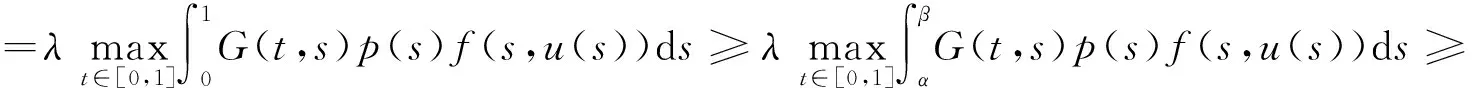
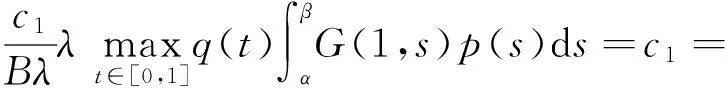
由定理1可知,存在u*∈K使得Tλu*=u*,且c1≤‖u*‖≤c2。由于p(s)f(s,0)>0,G(t,s)>0,t,s∈(0,1),得u*(t)=(Tλu*)(t)>0,t∈(0,1),從而u*(t)是BVP(1)的正解。
2 主要結論
記:
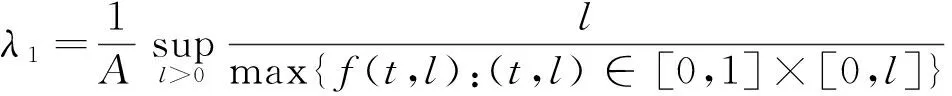
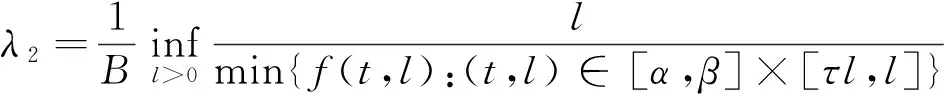
定理2 若λ2<λ1,則對任意的λ∈(λ2,λ1),BVP(1)至少有1個正解。
證明 由λ∈(λ2,λ1),則存在0 需要證明a≠b。若不然,即a=b,有: 由A>B且 min{f(t,l):(t,l)∈[α,β]×[τa,a]}≤max{f(t,l)∈[0,1]×[0,a]}, 從而產生矛盾。由引理4知BVP(1)至少有1個正解u1,a≤‖u1‖≤b。 定理3 若f0=f∞=∞,則對任意的λ∈(0,λ1),BVP(1)至少有2個正解。 證明 記: (5) 另一方面,由f0=f∞=∞,存在b1,b2,0 即 這樣找到了兩對數(shù)對{b1,a1},{a2,b2}使得: 由引理4知BVP(1)至少有2個正解u1,u2,b1≤‖u1‖≤a1 定理4 若f0=f∞=0,則對任意的λ∈(λ2,∞),BVP(1)至少有2個正解。 證明 記: (6) 由引理4知BVP(1)至少有2個正解u1,u2,a1≤‖u1‖≤b1 設u∈K是BVP(1)的解,則有: 從而產生矛盾,得證。 設u∈K是BVP(1)的解,則有: 從而產生矛盾,得證。 例1 考慮邊值問題: 例2 考慮邊值問題: 經計算M=276 480,由定理6知對任意的λ∈(276 480,∞),BVP(1)不存在正解。 /References: [1] BAI Zhanbing, WANG Haiyan. On positive solutions of some nonlinear fourth-order beam equations[J].Journal of Mathematical Analysis Applications & ications, 2002, 270(2):357-368. [2] LIU Yansheng. Multiple positive solutions of nonlinear singular boundary value problem for fourth-order equations[J]. Applied Mathematics Letters, 2004, 17(7): 747-757. [3] 閆東明.一類四階兩點邊值問題多個正解的存在性[J].工程數(shù)學學報,2010,27(1):133-138. YAN Dongming. Existence of multiple positive solutions for a class of fourth-order two-point boundary value problems[J]. Chinese Journal of Engineering Mathematics, 2010, 27(1): 133-138. [4] 索秀云,郭少聰,張繼葉,等.四階非局部邊值問題方程組正解的存在性[J].河北科技大學學報,2012,33(3):197-206. SUO Xiuyun, GUO Shaocong, ZHANG Jiye, et al. Existence of positive solutions for nonlocal fourth order boundary value problem systems[J]. Journal of Hebei University of Science and Technology, 2012, 33(3): 197-206. [5] 楊飛,劉玉敬,郭彥平.含有一階導數(shù)的非局部四階邊值問題正解的存在性[J].河北科技大學學報,2012,33(4):283-289. YANG Fei, LIU Yujing, GUO Yanping. Positive solutions to nonlocal fourth-order boundary value problems with dependence on the first order derivative[J]. Journal of Hebei University of Science and Technology, 2012, 33(4): 283-289. [6] WANG Qi, GUO Yanping, JI Yude. Positive solutions for fourth-order nonlinear differential equation with integral boundary conditions[J].Discrete Dynamics in Nature and Society, 2013(96):292-297. [7] 吳紅萍,馬如云.一類四階兩點邊值問題正解的存在性[J].應用泛函分析學報,2000,2(4):342-348. WU Hongping, MA Ruyun. Positive solutions of fourth-order two-point boundary value problem[J]. Acta Analysis Function Alis Applicata, 2000, 2(4): 342-348. [8] 馬如云,吳紅萍.一類四階兩點邊值問題多個正解的存在性[J].數(shù)學物理學報,2002,22A(2):244-249. MA Ruyun, WU Hongping. Positive solutions of fourth-order two-point boundary value problem[J]. Acta Mathematica Scientia, 2002, 22A(2): 244-249. [9] YAO Qingliu. Positive solutions for eigenvalue problems of fourth-order elastic beam equations[J]. Applied Mathematics Letters, 2004, 17(2): 237-243. [10]閆東明.一類四階兩點邊值問題正解的存在性[J].應用數(shù)學學報,2010,33(6):1113-1122. YAN Dongming.Positive solution for a class of fourth-order two-point boundary value problem[J].Acta Mathematicae Applicatae Sinica, 2010,33(6):1113-1122. [11]ZHAI Chengbo, SONG Ruipeng, HAN Qianqian. The existence and the uniqueness of symmetric positive solutions for a fourth-order boundary value problem[J]. Computers and Mathematics with Applications, 2011, 62(6): 2639-2647. [12]LI Shunyong, ZHANG Xiaoqin. Existence and uniqueness of monotone positive solutions for an elastic beam equation with nonlinear boundary conditions[J]. Computers and Mathematics with Applications, 2012, 63(9): 1355-1360. [13]WANG Wenxia, ZHENG Yanping, YANG Hui, et al. Positive solutions for elastic beam equations with nonlinear boundary conditions and a parameter[J]. Boundary Value Problems,2014, 2014(1): 80. [14]陸海霞,孫經先.一類四階非線性微分方程兩點邊值問題的正解[J].數(shù)學的實踐與認識,2014,44(8):229-235. LU Haixia, SUN Jingxian. Positive solution of two-point boundary value problems for fourth-order nonlinear differential equation[J]. Mathematics in Practice and Theory, 2014, 44(8): 229-235. [15]鞠夢蘭,王文霞,郝彩云.一類四階兩點邊值問題正解的存在性[J].成都大學學報(自然科學版),2016,35(1):37-40. JU Menglan, WANG Wenxia, HAO Caiyun. Existence of positive solution to fourth-order two-point boundary value problem[J]. Journal of Chengdu University(Natural Science), 2016,35(1): 37-40. [16]葛渭高.非線性常微分方程邊值問題[M].北京:科學出版社,2007. [17]SUN Yongping. Positive solution of singular third-order three-point boundary value problem[J]. Journal of Mathematical Analysis and Applications, 2005, 306(2): 589-603. [18]LI Shuhong. Positive solutions of nonlinear singular third-order two-point boundary value problem[J]. Journal of Mathematical Analysis and Applications,2008, 323(11):413-425. [19]張海娥.帶積分邊界條件的奇異三階邊值問題的單調正解[J].唐山學院學報,2012,25(6):37-39. ZHANG Haie.Monotone positive solutions for singular third-order BVPs involving integral boundary conditions[J]. Journal of Tangshan College, 2012, 25(6): 37-39. [20]郭大均.非線性泛函分析[M].第2版.濟南:山東科學技術出版社,2001. Existence of positive solutions to a class of elastic beam equations JU Menglan, WANG Wenxia, HAO Caiyun (Department of Mathematics, Taiyuan Normal University, Jinzhong, Shanxi 030619, China) Elastic beam is a kind of mathematical model in elastic mechanics and engineering physics. For now, this type of model is often used in real life. On the basis of the relative research on the elastic beam equations with one end fixed and one end sliding support, and the multiple solutions of the elastic beam equation are researched. In this paper, through putting this problem into an integral equation, which is equivalent to an operator fixed-point problem, and combining with the properties of Green function and Guo- Krasnoselskii fixed point theorem of cone expansion and compression, the existence of positive solutions of this kind of elastic beam equations is discussed. Under various assumptions on nonlinear terms, the intervals of the parameters are established, and the existence of one positive solution, two positive solutions or nonexistence of positive solutions for this elastic beam equations are obtained. In conclusion, the intervals of eigenvalue about this problem for at least one positive solution, two positive solutions and nonexistence of positive solutions are obtained. The study of the existence of such solution can not only contribute to the stability analysis of elastic beams, but also enrich the theory of material mechanics. nonlinear functional analysis theory; elastic beam; positive solution; Guo-Krasnoselskii fixed-point theorem; material mechanics 1008-1542(2017)02-0131-06 10.7535/hbkd.2017yx02005 2016-05-16; 2016-12-28;責任編輯:張 軍 國家自然科學基金(11361047) 鞠夢蘭(1991—),女,重慶人,碩士研究生,主要從事非線性算子方面的研究。 王文霞教授。E-mail:wwxgg@126.com O175.8 MSC(2010)主題分類:34B05 A 鞠夢蘭,王文霞,郝彩云.一類彈性梁方程正解的存在性[J].河北科技大學學報,2017,38(2):131-136. JU Menglan,WANG Wenxia,HAO Caiyun.Existence of positive solutions to a class of elastic beam equations[J].Journal of Hebei University of Science and Technology,2017,38(2):131-136.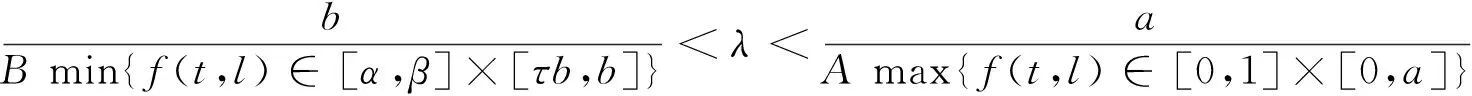

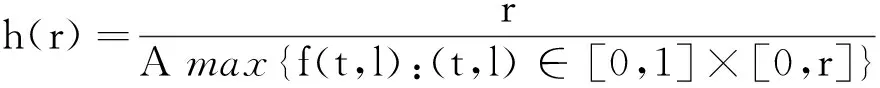
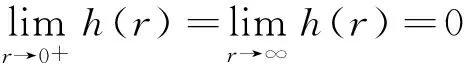
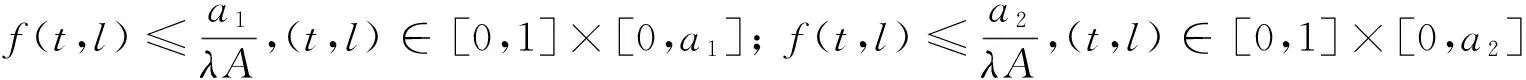
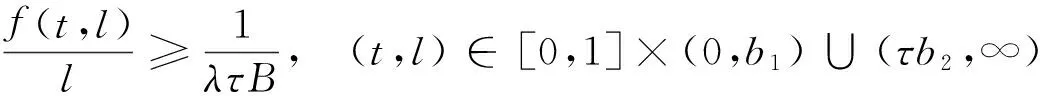
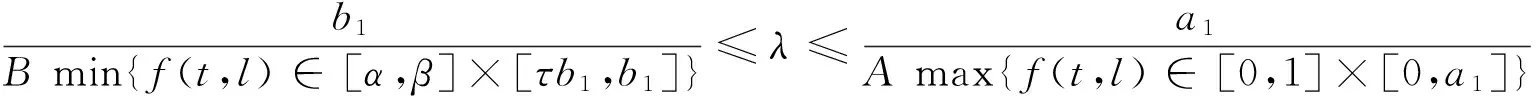
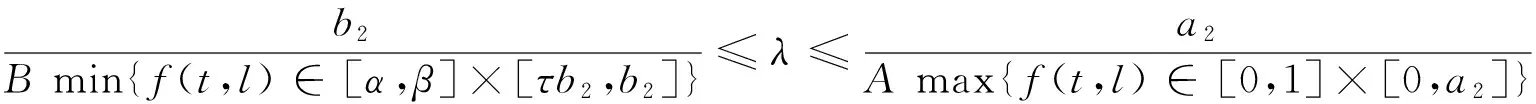
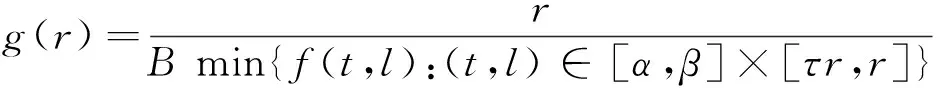

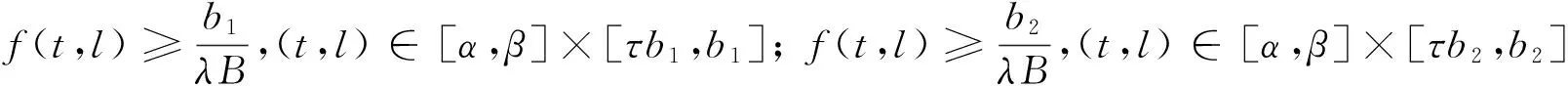
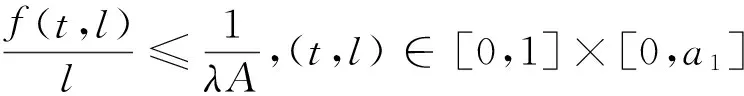
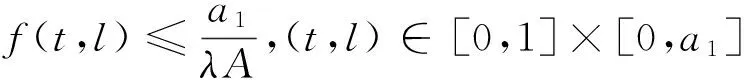
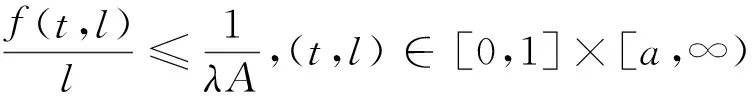
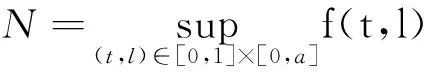
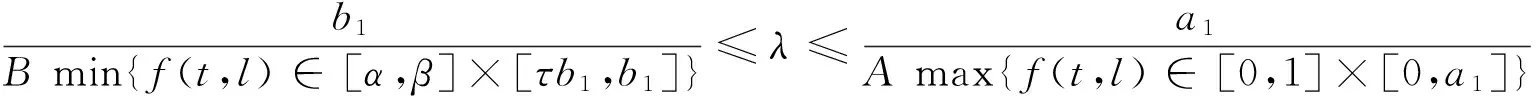
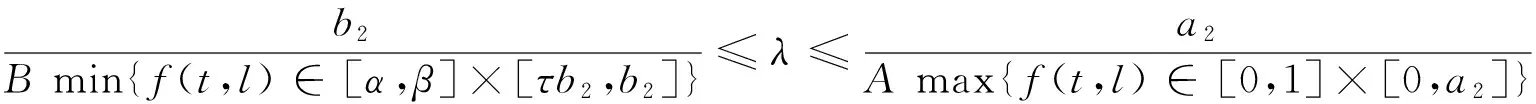
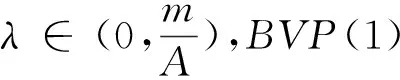
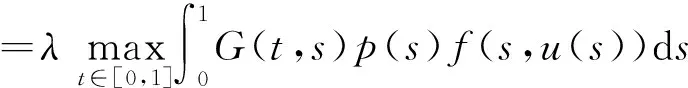
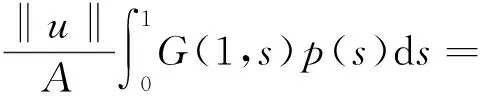
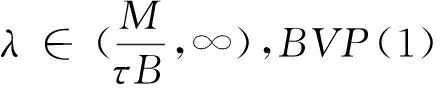
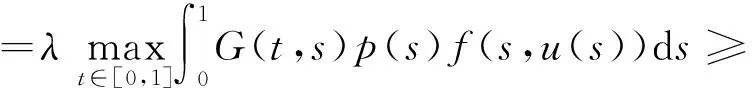
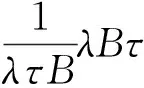
3 例子