高中數(shù)學(xué)教學(xué)中如何運(yùn)用數(shù)學(xué)歸納法
內(nèi)蒙古包頭市回民中學(xué)(014040) 郜春燕 ●
高中數(shù)學(xué)教學(xué)中如何運(yùn)用數(shù)學(xué)歸納法
內(nèi)蒙古包頭市回民中學(xué)(014040) 郜春燕 ●
在新的高中數(shù)學(xué)教學(xué)課標(biāo)中,提出了培養(yǎng)學(xué)生綜合分析能力方面的要求.而面對(duì)這一要求,就需要教師在教學(xué)中充分合理的使用數(shù)學(xué)歸納法.基于此,文章首先介紹了數(shù)學(xué)歸納法的具體含義,進(jìn)而根據(jù)實(shí)際的例題展開(kāi)了數(shù)學(xué)歸納法的具體應(yīng)用方式探討.
高中數(shù)學(xué);教學(xué);運(yùn)用;數(shù)學(xué)歸納法
數(shù)學(xué)歸納法是一種在高中數(shù)學(xué)中十分重要的解題方式,其在很多類(lèi)型的證明題中均有很好的應(yīng)用效果.作為一名高中數(shù)學(xué)教師,有必要在教學(xué)中通過(guò)理論講解、例題分析等多種方式對(duì)數(shù)學(xué)歸納法的應(yīng)用途徑展開(kāi)講解,進(jìn)而幫助學(xué)生掌握數(shù)學(xué)歸納法,從而提升數(shù)學(xué)解題能力.
一、數(shù)學(xué)歸納法的含義
數(shù)學(xué)歸納法在高中數(shù)學(xué)的整體知識(shí)體系中,主要應(yīng)用于一些與自然數(shù)有關(guān)的證明問(wèn)題中,屬于一種邏輯上的推斷證明方法,在高中數(shù)學(xué)中有著極其廣泛的應(yīng)用,需要我們教師在教學(xué)中傳授于學(xué)生.?dāng)?shù)學(xué)歸納法在使用時(shí),需要分為兩步進(jìn)行證明,首先往往需要證明某一個(gè)特殊值,例如0、1等,在需要證明式子里成立,進(jìn)而在假設(shè)n= k時(shí)成立的基礎(chǔ)上,證明出n=k+1時(shí)式子也成立,所以式子恒成立.教師在教學(xué)時(shí),需要嚴(yán)格地讓學(xué)生認(rèn)知到,在數(shù)學(xué)歸納法使用時(shí),需要分為兩步證明,首先找出特殊值;進(jìn)而假設(shè)n=k時(shí)成立,在此基礎(chǔ)上再證明n=k+1也成立.這種使用遞推證明的方式,就是完全歸納的推理,能夠?qū)崿F(xiàn)題目的證明.
二、具體應(yīng)用
1.?dāng)?shù)學(xué)歸納法在幾何問(wèn)題中的應(yīng)用
在高中數(shù)學(xué)的幾何部分,數(shù)學(xué)歸納法主要有三個(gè)部分的應(yīng)用,其一是應(yīng)用數(shù)學(xué)歸納法證明題目;其二是應(yīng)用數(shù)學(xué)歸納法制作幾何圖形;其三為應(yīng)用數(shù)學(xué)歸納法作為計(jì)算工具.以下以一道例題展開(kāi)講解.
例1 已知一平面內(nèi)有n條直線,并且任意兩條直線均相交,而任意三條直線均不存在共交點(diǎn),請(qǐng)證明在該平面內(nèi)n條直線一共有Pn=n(n-1)/2個(gè)交點(diǎn).
首先題目中說(shuō)明任意兩條直線均相交,故此不存在平面內(nèi)只有一條直線的情況,因此在題目解答上可以分為兩個(gè)情況進(jìn)行討論.
首先當(dāng)n=2時(shí),交點(diǎn)為1,代入Pn=n(n-1)/2也為1,所以成立.
其次當(dāng)n≥2時(shí),假設(shè)Pn=n(n-1)/2是成立的,如果此時(shí)再增加一條直線,根據(jù)題目在平面內(nèi)任意兩條直線均相交,可知此時(shí)又會(huì)增加n個(gè)交點(diǎn),因此有
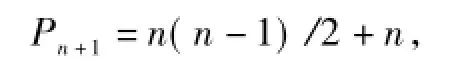
整理得
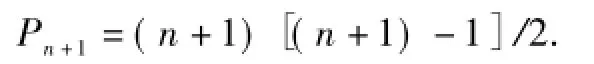
因此在n+1條時(shí)也成立
所以在該平面內(nèi)n條直線一共有Pn=n(n-1)/2個(gè)交點(diǎn).
2.?dāng)?shù)學(xué)歸納法在整除類(lèi)問(wèn)題中的應(yīng)用
對(duì)于整除類(lèi)問(wèn)題,教師在講解時(shí)也可以結(jié)合數(shù)學(xué)歸納法進(jìn)行講解,提升學(xué)生對(duì)該類(lèi)問(wèn)題的解題效率.以下以一道例題展開(kāi)講解.
例2 對(duì)于任意自然數(shù)n,求證p=26n+1+9n+1能被11整除.
證明 (1)當(dāng)n=0時(shí),p=2+9=11,能被11整除.
(2)假設(shè)n=k(k∈N)時(shí),11|(26k+1+9k+1),當(dāng)n=k +1時(shí),
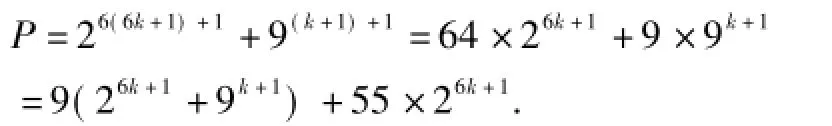
由假設(shè)知11|9(26k+1+9k+1),又11〗(55×26k+1),從而知p=26(k+1)+1+9(k+1)+1可被11整除.
由(1)和(2)可知,當(dāng)n是任意自然數(shù)時(shí)命題成立.
綜上所述,數(shù)學(xué)歸納法在高中數(shù)學(xué)的知識(shí)體系中屬于極其重要的一種題目求證方式,需要我們每一位教師在教學(xué)中均采取合理的措施傳授于學(xué)生.文章主要詳細(xì)介紹了數(shù)學(xué)歸納法在幾何證明題、整除證明題中的應(yīng)用,除此之外,數(shù)學(xué)歸納法在不等式、恒等式、數(shù)列問(wèn)題以及代數(shù)式證明題中均有明顯的應(yīng)用效果,值得每一位教師充分展開(kāi)教學(xué).
[1]曾饒利.?dāng)?shù)學(xué)歸納思想在高中數(shù)學(xué)教學(xué)中的應(yīng)用[J].新課程·中學(xué),2015,12(12):60.
[2]梁旭峰.勤思索,善歸納——高中數(shù)學(xué)中歸納思維的培養(yǎng)[J].新課程·中旬,2013,11(12):46-46,47.
[3]李敬年.如何提高高中生的數(shù)學(xué)思維能力[J].新課程學(xué)習(xí)·中旬,2014,22(7):87-87.
G632
B
1008-0333(2017)06-0035-01

