基于突變理論的巖質邊坡失穩預警模型

郭朝旭

(1．福建省建筑科學研究院 福建省綠色建筑重點實驗室 福建福州 350025;2.福州大學 福建福州 350108)

基于突變理論的巖質邊坡失穩預警模型

郭朝旭1,2

(1．福建省建筑科學研究院 福建省綠色建筑重點實驗室 福建福州 350025;2.福州大學 福建福州 350108)

以某巖質邊坡為例，利用FLAC有限差分軟件分析不同折減系數下位移變形特征，然后利用尖點突變理論分析巖質邊坡的臨界折減系數，從而建立巖質邊坡失穩判斷新的預警模型。

巖質邊坡；預警模型；突變理論

0 引言

邊坡的穩定性評判是一個艱難而復雜的過程，因為邊坡的穩定性是邊坡地質環境和人為因素共同作用的結果，且這些因素很大程度上又具有可變性、不確定性和隨機性等特點。當前，關于邊坡的穩定性評價方法大致可分為以下兩種：確定性分析方法和不確定性分析法[1～6]。由于邊坡穩定性的影響因素較多，且各個因素之間的關系又具有不確定性，因此在邊坡穩定性評價過程中就帶有一定的模糊性和不確定性。邊坡破壞必然會伴隨著一些比較直觀或者潛在的變化，如裂縫及位移的產生。這些變化與邊坡的穩定性之間存在一定的內在聯系。如果能夠準確地掌握這些變形與邊坡穩定性之間的關系，便能迅速地對邊坡的穩定狀態加以判斷，從而減少由此帶來的一些不必要的損失。

本文以FLAC有限差分軟件為基礎，對比分析不同強度折減系數條件下邊坡的最大位移變化趨勢，然后利用突變理論對該位移變化情況進行對比分析，得到位移突變條件下的強度折減系數，從而判斷該邊坡的穩定狀態。

1 位移預警模型

邊坡發生變形是一個連續的過程，但邊坡的破壞往往是在一瞬間完成的，在這個過程中，邊坡的位移會有突變現象產生，以點的位移突變作為評判邊坡穩定性的依據具有非常明顯的物理意義，而且直觀可靠，為了減少主觀因素的影響，本文選擇邊坡的最大豎直位移作為分析研究的基礎，根據突變理論，以尖點突變模型為原型建立評判標準。

(1)突變理論簡介

1972年法國數學家Thom創立了突變理論，該理論建立在拓撲動力學、微積分、奇點理論以及結構穩定性等數學理論之上，用來描述自然界中大量存在的不連續的突然變化現象，其特點是，根據一個系統的勢函數將它的臨界點進行分類，研究各類臨界點附近非連續變化處的特征，從而歸納出突變模型[1～2]。

(2)評判標準的建立

本文以Flac3D軟件為基礎對邊坡的位移變形進行計算分析，在巖土體材料強度不同折減系數下分別進行計算，以往往往利用數值計算的收斂性、特征部位位移的突變性及塑性區的貫通性作為邊坡失穩的判斷依據[5]。然而，以上各種方法未能建立統一標準，根據突變理論，釆用尖點突變模型，對Flac3D下的邊坡強度折減法計算過程中得到的邊坡最大位移進行分析，構建邊坡位移失穩破壞的突變模型，從而構建邊坡位移發生突變時的強度折減系數即穩定性系數，反映邊坡在各工況條件下的狀態。建立邊坡各強度折減工況下最大位移與折減系數的突變模型如式(1)所示：

δ=F(k)

(1)

折減系數的分級取值，可得到相應級數下的最大豎直位移，對每級的折減系數和最大豎直位移進行多項式擬合，就構建出下式的表達式，經分析，取5次式時，可滿足精度要求如式(2)所示：

δ=a0+a1k+a2k2+a3k3+a4k4+a5k5

(2)

對上式求導得勢函數如式(3)所示：

V=a1+2a2k+3a3k2+4a4k3+5a5k4

(3)

令q=a4/5a5,k=p-q，并帶入上式可以得到如式(4)～(8)所示：

V=b0+b1p+b2p2+b4p4

(4)

b0=5a5q4-4a4q3+3a3q2-2a2q+a1

(5)

b1=8a4q2-6a3q+2a2

(6)

b2=30a5q2-12a4q+3a3

(7)

b4=5a5

(8)

(9)

式(9)為以u,v為控制變量的正則尖點突變模型和對偶尖點突變模型的標準勢函數。對式(9)求導，令導數為0，如式(10)所示：

r3+ur+v=0(正則),-r3+ur+v=0(對偶)

(10)

把上式決定的臨界點集稱為平衡曲面，其在(r,u,v)空間中的圖形，上下葉穩定，中葉不穩定，無論u,v沿什么途徑變化，相點(r,u,v)只在上葉或者下葉平衡的變化，當相點(r,u,v)到達上下葉邊緣時發生突跳躍過中葉，因此，在平衡曲面豎直切線的點構成狀態的突變點集，其方程為如式(11)所示：

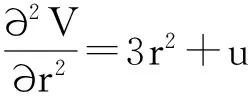
(11)

聯立上述兩式，消去r，得到所以對于邊坡穩定有如下判據，Δ>0穩定，Δ<0不穩定，即判斷上述二次方程的實數根是否存在，通過對比可以得到式(12)～(13)：

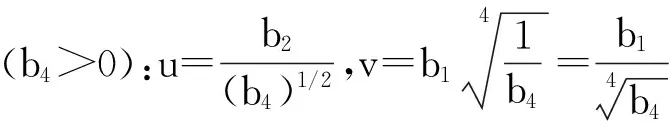
(12)

(13)

2 工程邊坡概況

以馬尾沿山公路邊坡B段中BK0+580-BK0+740段，邊坡最大高度約50m，屬高陡巖質邊坡。坡頂為馬尾區委黨校，邊坡北側為馬尾中學。該邊坡表層覆蓋層較薄，坡面基本為中微風化巖，坡面節理裂隙發育，邊坡整體穩定主要受結構面控制，如圖1所示。2015年8月開始坡面修正開挖施工，2015年11月完成開挖。支護方式：從上向下四級坡體，第一、二級錨桿長度為15m，用32mm的精軋螺紋管，錨固力200KN；第三、四級放坡，錨桿支護長度為12m，用兩根20mm的三級鋼鋼筋，錨桿與水平夾角為20°，錨固力100kN。

圖1 破碎巖體坡面

2.1 地層巖性

地貌單元主要為剝蝕殘山地貌單元，場地自上而下土層主要有：

(1)粉質粘土：灰黃色，硬塑，濕。以粘粒、粉粒為主。

(2)凝灰熔巖坡積粘性土：局部表現為殘積粘性土，為凝灰熔巖(J3n)風化殘積而成。褐黃、灰黃色、可塑、濕等特征，為凝灰熔巖(J3n)坡積而成。可見原巖殘余結構，具有遇水易軟化特征，主要由粘、粉粒組成，坡積成因。

(3)全風化凝灰熔巖(J3n)：淺黃色、灰白色，凝灰結構，散體狀構造，巖體裂隙極發育，巖芯呈土狀，手捏易散，遇水易軟化、崩解，巖石堅硬程度屬極軟巖，巖體完整程度屬極破碎。

(4)砂土狀強風化凝灰熔巖(J3n)：淺黃色、灰白色，凝灰結構，散體狀構造，巖體裂隙極發育，巖芯呈砂土狀，手捏易散，遇水易軟化、崩解，巖體完整程度屬破碎，巖體基本質量等級為Ⅴ級。

(5)碎塊狀強風化凝灰熔巖(J3n)：灰黃色，凝灰結構，碎裂狀構造，巖體隙裂極發育，巖芯呈碎塊狀，巖石堅硬程度屬較軟巖，巖體完整程度屬破碎，巖體基本質量等級為Ⅴ級。

(6)中～微風化凝灰熔巖(J3n)：局部表現為變粒巖和淺粒巖。淺灰色、褐紫色，凝灰質結構，塊狀構造，巖石裂隙較發育，巖石堅硬程度屬較硬巖，巖體完整程度屬較完整-較破碎，巖體基本質量等級為Ⅲ-Ⅳ級。

2.2 水文地質條件

地下水類型主要包括：

(1)上層滯水：主要賦存于雜填土中，地下水量一般，補給主要為大氣降水及地表徑流入滲，排泄方式主要向地勢低處側向排泄，部分為蒸發和下滲。

(2)基巖孔隙-裂隙水：主要為賦存于風化巖中的裂隙水，由于風化程度不同，風化裂隙率和連通性差異較大，其透水性不均勻，總體透水性較弱，富水性也較弱。

3 位移預測結果與坡體穩定狀態

為了對該模型進行驗證和分析，采用FLAC快速有限差分軟件對馬尾區沿山通道二期邊坡工程19-19’剖面進行分析，觀察在不同折減系數條件下巖土體的最大位移情況，利用本文提出的基于尖點突變模型的邊坡失穩機制判別模型對該邊坡進行安全穩定性評價。計算參數如表1所示，模型及結果詳見圖2～圖4。

表1 計算參數

圖2 Flac模型簡圖(左側為巖土體模型，右側為支護模型)

圖3 不同強度折減系數條件下x方向位移分布

圖4 不同強度折減系數條件下剪應變增量分布

圖5為豎直方向最大位移和折減系數圖，根據上文討論，由式(對折減系數和最大位移進行多項式進行擬合，由圖5可知，突變在1.4左右，所以，列出各級擬合的計算過程，詳細說明尖點突變模型的計算方法。

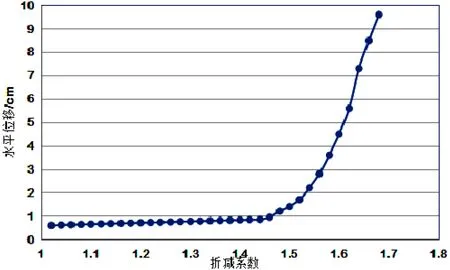
圖5 最大位移和折減系數圖

擬合級數和△的值如表2、圖6所示。由圖6可見，隨著擬合級數的增加，逐漸減小，據前面分析可知時當△>0時邊坡為穩定，當△≤0時，邊坡就處于不穩定狀態了，因此通過上圖的分析可以看出，在折減系數為1.42時，邊坡處于穩定狀態，而1.44時邊坡就失穩了，這時雖然位移突變模型有解，但得到的無意義的物理值，因此此時邊坡的穩定系數可確定為1.42，而此折減系數條件下的位移最大發生在坡面中部位置，水平位移為8.45mm(此邊坡變形預警值為邊坡支護完成后的位移數值)，因此可以通過檢測該部位的位移，結合位移監控預測模型，可以對邊坡進行風險評估和預測。

表2 擬合級數、對應折減系數與△的值 個

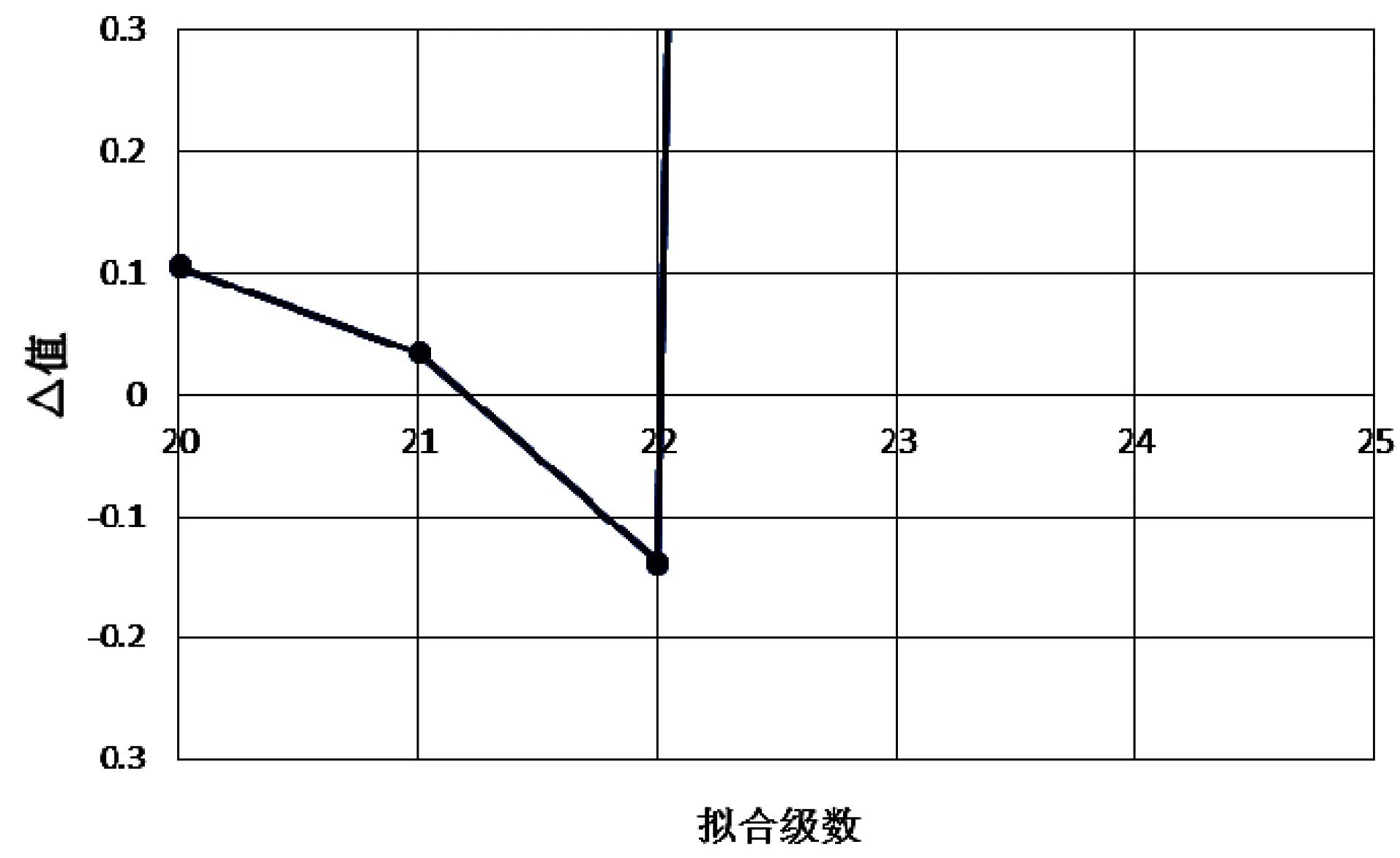
圖6 擬合級數和△的值

因此，可以通過降低結構面的參數，從而得到坡體的位移；而該位移與邊坡穩定性的關系是通過尖點突變理論建立的聯系，這樣在今后可以對位移進行監測或者結構面控制的巖質邊坡位移進行神經網絡訓練分析，從而得到不同折減系數下邊坡的最大位移，根據尖點突變模型獲取邊坡的穩定性，從而實現可以評判由結構面控制的巖質邊坡的穩定性，避免現有安全系數評判的不合理和不確定性。判別流程如圖7所示。

圖7 邊坡位移預警模型分析流程

4 結語

通過對巖質邊坡安全監控模型的研究，總結并建立了巖質邊坡監控預測模型，并根據巖質邊坡失穩破壞機理，建立了基于尖點突變理論的邊坡穩定性評價模型，可以為巖質邊坡監測——預警——評估體系提供另一種思路和解決方法，具體如下：

利用快速拉格朗日有限差分軟件FLAC對邊坡進行位移計算，這里通過強度折減法折減結構面或坡體材料參數獲取不同折減系數條件下邊坡的最大位移以及所處的位置；建立不同條件系數與最大位移的關系，利用尖點突變模型分析邊坡的失穩臨界狀態，即失穩臨界位移值，從而建立邊坡臨界最大位移，位移所處的位置與位移監測量的關系；同時可以利用監控量預測模型(神經網絡與灰色模型)對邊坡的穩定性進行預測分析。

[1] 黃昌乾,丁恩保.邊坡工程常用穩定性分析方法[J].水電站設計,1999,15(1):53-58.

[2] 李世海,劉天蘋,劉曉宇.論滑坡穩定性分析方法[J].巖石力學與工程學報,2009,28(2).

[3] 魏麗敏,何群,林鎮洪.考慮地下水影響的滑坡穩定性分析[J].巖土力學,2004,25(3):422-426.

[4] 莫偉偉,徐平,丁秀麗.庫水位漲落對滑坡穩定性影響研究進展[J].地下空間與工程學報,2006,2(6):997-1002.

[5] 程杰.基于變形數據的邊坡穩定性評判方法研究[D].重慶：重慶交通大學,2014.

[6] Carrara A, Cardinali M, Detti R, et al. GIS techniques and statistical models in evaluating landslide hazard[J].Earth surface processes and landforms,1991,16(5):427-445.

A Instability Prediction Model for Rocky Slope Based on Catastrophe Theory

GUOChaoxu1,2

(1.Fujian Academy of Building Research, Fujian Key Laboratory of Green Building Technology,Fuzhou 350025; 2.Fuzhou University, Fuzhou 350108)

Taking a rock slope as an example, its stability had been predicted by using Flac 3D software under different on reduction factors. Then the critical safety coefficient was analyzed by catastrophe theory. This method is different from the common strength reduction method, and verified to be suitable for rock slope.

Rock slope; Forewarning model; Catastrophe theory

郭朝旭(1987.8- )，男，工程師。

E-mail:guochaoxu177@163.com

2016-12-19

TU472

A

1004-6135(2017)03-0068-04