空間飛行器動力學與控制研究綜述

劉付成,朱東方,黃 靜

(1.上海市空間智能控制技術重點實驗室,上海 201109; 2.上海航天控制技術研究所,上海 201109)

?

空間飛行器動力學與控制研究綜述

劉付成1，2,朱東方1，2,黃 靜1，2

(1.上海市空間智能控制技術重點實驗室,上海 201109; 2.上海航天控制技術研究所,上海 201109)

概括介紹了近年來空間飛行器的動力學與控制研究的發展狀況，綜述了單星動力學建模和控制技術、多星動力學建模和控制技術，以及太陽帆航天器、繩系衛星等新型航天器動力學與控制技術等相關航天領域中的若干基礎問題，總結了在這些領域中的研究方法及取得的成果。提出了相關領域中值得深入研究的問題及后續發展方向，如深空探測的軌道動力學、超大尺度柔性航天器的動力學建模與協同控制技術、敏捷衛星的機動控制技術、多星姿軌耦合動力學和控制技術、太陽帆航天器動力學與控制技術，以及空間繩系衛星系統的動力學與控制技術等重點和主要發展方向。

空間飛行器； 動力學； 軌道控制； 姿態控制； 剛體； 柔性； 姿軌耦合； 敏捷衛星； 太陽帆航天器； 繩系衛星

0 引言

空間飛行器從最初結構簡易、功能單一的衛星發展到現在構型復雜、功能多樣的衛星，在人類探索空間、認識宇宙的過程中承擔了越來越重要的任務，并對人類的生產和生活產生了深遠的影響。空間飛行器的動力學與控制技術是空間飛行器順利執行空間探測任務的基礎和保障，在航天技術發展中起著舉足輕重的作用。隨著空間探索任務的不斷發展，空間飛行器的結構和功能越來復雜，技術發展越來越迅猛，涉及的領域也越來越多。空間飛行器動力學與控制的研究內容涵蓋面非常廣，本文從單星任務、多星任務，以及新型航天器任務出發，對每個任務領域涉及的動力學與控制技術進行了概括介紹，并對今后空間飛行器動力學與控制領域的研究內容進行了展望。

1 單星動力學與控制技術

本章介紹了單顆空間飛行器在軌執行任務時面臨的軌道動力學、軌道控制技術、姿態動力學和姿態控制技術。其中：在軌道動力學和控制領域對近地軌道器和深空探測器兩種任務層面進行了分析；在姿態動力學與控制領域對剛體航天器、柔性航天器等航天器本身特性進行了分析。

1.1 軌道動力學

1.1.1 近地軌道動力學

一般將近地軌道器(人造衛星)運動過程力學系統轉為受攝二體問題[1]。對受攝二體問題，參考軌道采用開普勒軌道，實際運動則為緩慢變化的開普勒軌道，相應的運動狀態，在任何時刻都可用瞬時開普勒軌道描述。該方法通常是利用常數變易法轉為小參數方程，根據常微解析理論(邦加雷定理)構造所需的解析解。在常數變易中，基本參數通常是采用二體問題完整解中有明確軌道幾何意義的積分常數，6個開普勒軌道要素(半長軸a，偏心率e，軌道傾角i，升交點赤經Ω，近地點幅角ω，平近點角M)，經過常數變易后轉為小參數方程對應的初值問題，小參數方程常見形式包括以攝動加速度表達的Gauss型、以攝動函數表達的Lagrange型和以正則共軛變量表達的Delaunay型等三類。對受攝二體問題滿足的小參數方程，無論其具體形式，均可采用經典攝動法(或各種改進的攝動法)構造相應的小參數冪級數解。

航天器軌道計算通常有解析法(如擬平均要素法)和數值積分法(如Cowell法)，解析法計算簡單，但精度較差，而數值積分法特別是Cowell法精度較高，但計算量較大，因此需對模型進行簡化以減少計算量[2]。

1.1.2 深空軌道動力學

深空探測器(探測大行星、小行星或自然衛星)的運動，主要力源是太陽，或太陽和一個行星，或目標行星及其一個自然衛星等。除主要力源外，其它力源(包括上述非質點引力和非引力等)均可處理成攝動源，即小擾動。因此，根據其力源環境不同，深空探測器的軌道動力學一般有兩種處理方式。一種是僅考慮深空探測器飛行過程中的一個主要力源，將其作為受攝二體問題，這是行星際軌道設計的一般思路，HOWARD在其所著《Orbital Mechanics for Engineering Student》中對深空探測器的行星際軌道動力學進行了詳盡的說明與介紹。另一種是考慮深空探測器飛行過程中的兩個主要力源，將其作為受攝的限制性三體問題。文獻[3]以受攝的限制性三體問題為基礎，對深空探測器運動的軌道動力學基礎進行了系統研究。

另外在小天體的深空探測中，小行星本身的特殊形狀導致了其引力場的特殊性。在探測器逐漸接近小行星的過程中，小行星引力場已不能單純視作中心引力場。為更精確地描述其引力特性，可將小行星視作多個引力中心的組合，如在日本的隼鳥(Hayabusa)探測器附著糸川(Itokawa)小行星時，就將小行星視作6個球形引力體的組合，如圖1所示[4]。

多面體模型和質點群模型是目前最精確的小天體模型。這兩種建模方法的發展和完善使對小天體附近軌道動力學問題獲得更準確和深入的研究，該模型由WERNER提出并發展成較完備的引力場建模方法[5]。基于多面體模型的216 Kleopatra和6 489 Golevka小天體模型如圖2所示。多面體近似模型的主要思想是用一個多面體或多個特定形狀的質量元組合逼近小行星的形狀，再通過積分變換將引力勢能中的三重積分轉為可計算的曲線和曲面積分。文獻[6]從不規則形狀小天體引力場的建模、小天體附近的自然軌道動力學、小天體附近的受控軌道動力學等方面對小天體附近軌道動力學與控制技術進行了研究。

綜上所述：近地軌道動力學技術較成熟，通常采用受攝二體問題模型，包括解析法和數值積分法；深空探測動力學一般采用軌道拼接方法，通過分段考慮中心力源，將探測器作為受攝二體問題進行解決，但部分特殊任務，如平動點探測，不能簡化為二體問題，需進一步開展受攝的限制性三體問題研究，而對小天體探測任務，因其特殊的形狀和體積，需深入開展基于多質心或多面體擬合模型真實還原小天體附近動力學環境的研究。

1.2 軌道控制技術

1.2.1 近地軌道控制技術

航天器的軌道控制是對航天器施以外力，有目的地改變其質心運動軌跡的過程。單顆航天器的軌道控制按應用方式可分為軌道機動和軌道保持兩種。

航天器軌道機動是使航天器從一個自由飛行軌道轉移至另一個自由飛行軌道。常見的軌道機動方法包括霍曼轉移和Lambert轉移。霍曼轉移常用于共面軌道轉移任務，其優點是轉移過程燃料消耗少，但使用范圍較窄；Lambert變軌是已知初值狀態、期望終端狀態和轉移時間，可實現任意軌道的轉移任務。在軌道機動中，既要快速(最小時間)、精確，又要能量或燃料消耗最少，均涉及最小能量法和最短時間法[7]。

航天器軌道保持是使衛星軌道維持在期望的位置，其目的是克服攝動影響，使航天器軌道的某些參數值保持在允許的范圍內，通常用于太陽同步對地觀測衛星的軌道保持和地球靜止軌道衛星的位置保持。軌道保持常用的方法有兩種：一是基于解析方程的特殊點修正的方法；另一是轉為相對虛擬衛星的相對控制問題。文獻[8]用解析法對太陽同步(準)回歸軌道衛星動力學特性進行了研究，分析了非球攝動、大氣阻力攝動和太陽引力諧振等主要攝動因素對衛星的影響，并通過對軌道要素的控制實現太陽同步(準)回歸軌道衛星的軌道保持。文獻[9]提出了一種地球同步軌道衛星多星共位技術，在單顆衛星在東西和南北方向位置保持控制的基礎上，使軌道傾角矢量差始終與相應的偏心率矢量差保持平行，實現多星共位，進而節約稀缺軌道資源的優勢。文獻[10]通過引入虛擬參考衛星，用模型控制方法(MPC)進行動態預測、滾動優化，在模型失配、環境變化情況下進行多變量優化，給出了一個最優的反饋增益序列，并通過采用開環和前饋-反饋閉環兩種形式的控制方程，將衛星軌道實時保持在偏差管道內。文獻[11]用線性離散系統最優控制理論，設計了最優狀態調節器進行軌道維持控制，具較高的控制精度和良好的收斂性。

1.2.2 深空軌道控制技術

深空軌道控制一般采用化學推進系統，在地面測控和天文自主導航的基礎上，進行脈沖推力的軌道修正，目前絕大多數的深空探測器采用了此類軌道控制方案。國外(尤其是美國)關于轉移軌道中途修正的研究已十分成熟，目前在技術途徑上很少有新的成果報道，有關方法和結論多體現在NASA的任務設計報告中[12]。文獻[13]針對深空探測軌道自主中途修正問題，提出了一種基于B平面參數的求解算法。

近年來隨著小推力推進系統的發展和完善，推進器壽命逐漸增加，比沖進一步增大，小推力軌道控制技術已開始被用于深空探測任務。1998年10月24日發射的深空一號(DS1)探測器是美國航天局(NASA)“新千年計劃”中的首顆探測器，也是世界上第一顆以電離子推進發動機為主推進的探測器，其成果為未來小推力發動機在深空探測軌道機動控制中的應用奠定了基礎[14]。日本于2003年5月9日發射的Hayabusa是第二顆采用太陽能電推進的探測器，Hayabusa探測器的實際工作壽命長達7年，任務期間離子推進系統工作超過40 000 h，共提供了約4.3 km/s的軌道控制速度增量[15]。

借力飛行是深空探測中軌道控制的又一項關鍵技術，其基礎由行星和彗星軌道攝動理論發展而來，借助于飛越的行星等天體獲取額外的速度增量。歐空局推出的登陸彗星的羅塞塔(ROSETTA)計劃是一個極為經典的借力飛行應用任務。該探測器于2004年3月2日發射升空，在為期10年的太空旅途中，探測器飛行經歷了火星借力1次和地球借力3次。

氣動力輔助軌道轉移的概念于20世紀60年代提出。1961年HORWARD提出氣動力輔助軌道轉移的意義與可行性，由此揭開氣動力輔助軌道轉移研究的序幕[16]。20世紀90年代，隨著NASA系列行星探測任務的進行，氣動捕獲技術獲得了很大發展。火星全球勘測器(MGS)、火星奧德賽探測器(ODY)、火星偵察軌道器(MRO)，這些深空探測器在進行探測任務過程中都成功應用了氣動輔助變軌技術[17-19]。

對火星等有大氣天體的著陸探測任務來說，進入、下降和著陸(EDL)階段的軌道控制是其中的關鍵，直接決定整個探測任務的成敗。歷次成功火星著陸探測任務進入段GNC主要采用基于IMU航位遞推的導航技術、RCS三軸穩定姿態控制、自旋穩定姿態控制、純彈道式進入、彈道升力式無制導進入，以及好奇號探測器采用的阿波羅式彈道升力式制導進入等[18]。下降段GNC主要采用慣性導航、RCS三軸姿態穩定控制、姿態晃動阻尼裝置等[20]。著陸段GNC主要采用雷達高度計/IMU組合導航、光學圖像/IMU組合導航、雷達測距測速/IMU組合導航、多項式制導、重力轉彎制導、標稱軌跡制導、RCS三軸姿態穩定控制、變推力發動機和固體反推火箭等[17]。好奇號探測器動力下降段采用了多項式制導和標稱軌跡制導，但由于其在著陸末段新采用了“空中吊車”著陸方式，因而其動力下降過程作了相應調整[21]。

月球由于無大氣環境，其著陸過程的軌道控制只能采用完全依賴主動推力減速的軌道控制方案。中國的嫦娥3號衛星采用了常推力燃耗次優顯式制導、4次多項式制導等制導控制方式，完成了7個任務階段的軌道控制任務[22]。文獻[23]對月球軟著陸的制導與控制進行了研究，以由極大值原理得出的最優著陸軌跡為基礎，給出了一種基于人工神經元網絡的非線性最優控制策略，設計了非線性閉環制導控制律，使著陸器按最優軌跡飛行。此方法基本可實現對最優軌跡的復現跟蹤。

圓型限制性三體問題中，在共線平動點附近，存在中心流形(實為條件穩定軌道，如Lissajous軌道、Halo軌道、擬Halo軌道等)和不變流形(穩定流形和不穩定流形)；在三角平動點附近，存在長周期軌道、短周期軌道和垂直周期軌道三種基本周期軌道類型[24]。目前已有多個深空任務實現了平動點軌道控制，ISEE3(1978年)、SOHO(1995年)、Genesis(2001年)等運行于日地L1點，MAP(2001年)、PLANK(2007年)、GAIA(2012年)等運行于日地L2點，中國的嫦娥2號衛星于2011年8月進入環繞地月L2點的Lissajous軌道[25-26]。

綜上所述：對單顆航天器的軌道機動任務，常用方法包括霍曼轉移和Lambert轉移，但為完成時間最優和燃料最優任務，需結合最優控制理論實現最優軌道機動控制；對單顆航天器的軌道保持任務，常用方法包括基于解析方程的特殊點修正和相對虛擬衛星的相對控制，其中基于解析方程的特殊點修正方法具燃料最省的優點，而基于相對虛擬衛星的相對控制可保證較高的保持控制精度，須根據能量消耗和控制精度綜合考慮。對深空探測任務的軌道控制，隨其飛行階段的環境特點和動力形式而不同。星際巡航階段化學推進可采用B平面參數求解算法，需重點解決中途修正和借力飛行問題；電推進需采用優化算法，重點解決連續推力方向的問題；地外天體捕獲制動階段目前研究重點集中于直接力與氣動力復合的減速策略；地外天體著陸任務主要集中于燃料最優的高精度著陸制導方法研究；平動點軌道主要集中于解決圓型限制性三體問題中的軌道保持策略。

1.3 姿態動力學

對航天器姿態動力學建模，根據是否考慮結構動力學影響，可歸為剛體航天器動力學建模和柔性航天器動力學建模。在剛體航天器動力學建模中，根據包含剛體數量的不同，可分為單剛體航天器動力學建模和多剛體航天器動力學建模；在柔性航天器動力學建模中，主要考慮剛體動力學和結構動力學交叉影響[27]。

1.3.1 剛體航天器姿態動力學

剛體航天器是一類帶剛度較高的太陽能帆板或天線結構，整體結構緊湊、柔性特征占比小的航天器。

對單剛體航天器，其姿態動力學模型相對較簡單，可直接用牛頓-歐拉或Lagrange分析力學等方法建立。所建立的動力學模型，姿態主要采用方向余弦、歐拉角或四元數、奇異值分解方法等進行描述[28]。

對多剛體航天器，可認為是由多個剛體基元以鉸鏈相互連接構成了一類較復雜的航天器，如帶多個對稱轉子的陀螺體衛星、帶剛硬太陽帆板的衛星、帶機械臂的空間站等[29]。多剛體航天器動力學建模問題可歸為無根樹多剛體動力學建模問題，主要包括空間結構關系描述和建模推導兩個方面。針對多剛體系統結構的空間連接關系描述，ROBERSON等基于圖論首次提出了一種通用性分析方法，即R-W方法。在多剛體系統結構的位置關系和空間姿態的描述中，文獻[30]通過將矢量與矢量矩整合為旋量(一個六維矢量)，提出了一種簡明的開鏈和閉鏈多剛體運動學與動力學分析的旋量方法。在建模推導中，文獻[31]基于達朗伯原理，結合矢量力學和分析力學，用廣義速率描述運動，建立了多剛體的動力學方程。文獻[32]提出濾波理論與多體系統動力學空間算子代數理論，建立了空間多剛體系統模型的動力學算子建模理論及遞推計算方法。文獻[33]基于空間算子代數符號體系，推導了適于航天器實時仿真的多體動力學遞推算法。

另外，針對多閉鏈剛體系統，文獻[34]用變分方法的高斯最小約束原理對邊界約束進行分析，避免了求解微分方程，降低了建模復雜度。

1.3.2 柔性航天器姿態動力學

隨著航天器的發展，星上安裝的大尺寸太陽能電池陣或天線載荷等柔性結構的質量和轉動慣量在航天器整體中的占比不斷上升，使結構動力學與剛體動力學間的交叉影響逐漸凸顯，出現了剛柔耦合航天器，如實踐五號、資源一號衛星和神舟系列飛船等航天器。另外，以大型薄膜衍射成像航天器為代表的新型復雜柔性天器，安裝的柔性結構的質量和轉動慣量等所占比重遠超過中心體，或僅由柔性結構構成。此類航天器屬柔性多體航天器，其結構動力學與剛體動力學間的交叉影響較剛柔耦合航天器更為凸顯，建模過程更復雜。

針對剛柔耦合航天器動力學建模，主要研究柔體變形與其大范圍空間運動間的相互作用或相互耦合，以及由這種耦合導致的動力學效應[35]。對剛柔耦合航天器，文獻[36]最早將結構動力學的有限元方法引入多體彈性動力學，推動了柔性航天器動力學建模技術發展，但未考慮多剛體系統動力學與結構力學間的耦合作用。文獻[37]用隨動坐標系給出多剛體系統動力學模型，根據矢量變分方法和虛功原理，建立了單開鏈和含閉環開鏈的柔性多體系統動力學模型，進一步發展了柔性航天器的動力學建模技術，但未描述物體大位移運動時構件彈性變形與大范圍運動的相互耦合作用。為解決該問題，LINKINS首次提出了對柔體描述的離散坐標法，通過模態坐標或有限元節點坐標直接描述物體的彈性變形，但該方法在對柔體離散時未考慮大范圍運動對其的影響，是一種零次近似意義的耦合[38]。為進一步解決大范圍運動對柔體離散描述時的影響，文獻[39]提出用混合坐標建立航天器動力學模型，即用離散坐標描述物體的剛體運動，模態坐標(即變形坐標)或有限元結點坐標描述物體的彈性變形。文獻[27]考慮柔性體與柔性體連接點間的復合位移變形，用混合坐標法建立了復合柔性結構航天器動力學模型。在上述理論發展的基礎上，文獻[40]對關于帶柔性附件的航天器姿態動力學與控制的研究成果進行了較全面的總結。國內同期也對柔體航天器動力學開展了大量研究，文獻[41-42]對剛柔耦合多柔體航天器的動力學建模問題進行了系統闡述。在柔體航天器動力學模型理論推導的基礎上，針對動力學方程的求解問題，主要發展了隱式算法如Newmark，Wilson-θ，Runge-Kutta等方法[43-45]。但當剛性程度過大(高低頻率之比大于1 000)時，動力學方程計算結果出現發散[46]。針對求解發散問題，文獻[47]提出了保辛攝動迭代算法，解決了剛體、柔體不同時間尺度積分造成的數值病態失真問題。

當剛柔耦合系統的運動速度增大到一定程度后會產生低階諧振現象，該現象被稱為動力剛化現象。其中，KANE在處理高速旋轉的懸臂梁動力學時得到錯誤結論，首次提出了動力剛化的概念，并通過平面細長梁的簡單偏微分形式表達位移-應變關系，驗證了動力剛化問題[48]。動力剛化的實質是作大范圍空間運動的柔性體因運動與變形間的相互耦合作用，導致柔性體剛度的增大(即附加動力剛度)。在該問題研究方面，文獻[49-50]較全面闡述了連桿柔性對高速機構動力學響應的影響。文獻[51]認為動力剛化現象的實質是柔性體剛度隨其應力而變，指出當物體進行大幅度空間運動時，外力、約束反力導致柔性體內部應力變大，產生動力剛化現象。文獻[52]認為柔性體剛度的減弱是變形的廣義坐標過早線性化導致的，通過精確到二階小量的運動學描述進行分析，得到了相同的結論。文獻[53]提出了解決動力剛化問題的一種數值方法，并進一步證明了子結構中柔性體的線性化假設成立。文獻[54]基于凱恩方程和休斯敦方法的柔性多體動力學建模理論，同樣也證明了柔性多體系統的動力剛化現象。

當剛柔耦合航天器的中心剛體也具柔體特性時，剛柔耦合航天器將轉成柔性多體航天器。針對多體動力學問題，文獻[55]系統闡述了多體動力學模擬和分析的研究進展。針對大型柔性結構振動動力學，文獻[56]用模態坐標描述柔性結構的節點位移，通過模態截斷縮減廣義自由度，提出了模態綜合建模方法。SHABANA等提出了柔性系統的動態子結構建模方法，進一步發展了柔性多體系統理論[57]。針對解決大范圍運動的柔性多體變形問題，文獻[58]結合連續介質力學和有限元方法，提出了絕對節點坐標法。同時，文獻[59]基于浮動坐標系，用絕對節點坐標法的建模理論，建立了大范圍空間運動與小變形柔性梁的剛柔耦合動力學模型。為解決計算效率不高的問題，文獻[60]基于絕對節點坐標方法分析基于第一類、第二類Piola-Kirchhoff應力張量推導獲得了彈性力及其Jacobi矩陣的解析表達式，通過對比研究給出了一種解決途徑。

綜上所述：對剛體衛星和柔性衛星姿態動力學建模的研究，主要集中于將結構作為連續體建模，分析影響整星動力學特性的主要因素，相關研究成果已在工程中得到了應用和驗證；對后續安裝柔性結構尺度和復雜度不斷增加的柔性衛星，柔性結構中存在的安裝間隙和膨脹預留間隙的影響將不可忽略，使碰撞動力學與結構動力學相互交叉，因此需深入研究此類非連續(間隙連接)柔性航天器的動力學建模方法。

1.4 單星姿態控制技術

1.4.1 單星穩態姿態控制技術

早期發展的衛星主要為動量衛星(如自旋衛星、雙自旋衛星和帶偏置動量飛輪衛星)，此類衛星具有陀螺定軸性[61]。對動量衛星的姿態穩定控制，主要是為消除星體章動對星上探測載荷高性能工作的影響，可通過利用噴氣控制、章動阻尼器或太陽光壓控制作用，實現對雙自旋衛星的穩定姿態控制。同時，為判定控制系統的穩定，根據雙自旋衛星的動力學方程，研究了姿態控制穩定性判據[62]。另外，針對自旋衛星和雙自旋衛星的重定向控制問題，開展了燃料消耗最優控制和大角度重定向控制研究[63-64]。研究者在分析太陽電池陣固有頻率和章動控制頻率的基礎上，給出了系統新的穩定性邊界，推動了此類衛星控制系統技術的發展[65]。

由于動量衛星平臺對有效載荷的應用限制較大，平臺控制精度較差，不利于滿足功能更復雜、性能更高的有效載荷發展需求，動量衛星逐漸被控制更靈活的零動量衛星替代。

a)零動量剛體衛星穩態姿態控制技術

根據執行機構配置，剛體航天器姿態穩定控制可分為全驅動和欠驅動兩種。對三軸穩定航天器來說，其姿態控制系統在3個軸向均配置執行機構(動量交換裝置或推力器)構成全驅動系統，即系統位形空間的維數與其控制輸入維數相同，欠驅動系統是指控制輸入維度低于其位形空間維數的系統。

(a)全驅動姿態控制技術

根據航天器運行狀態下的信息測量情況，可將全驅動控制分為全狀態反饋控制和輸出反饋控制。全狀態反饋控制是指航天器在運行狀態下的姿態和角速度信息均可通過敏感器測量獲得。近年來，為降低航天器制造成本或作為角速率敏感器失效后的備份方法，越來越多的研究致力于輸出反饋控制在航天器姿態控制領域中的應用，其中又以僅用姿態信息反饋作為主要研究內容。

航天器姿態控制研究初期，多數研究成果是先將系統的非線性模型作線性化處理，再用線性控制理論中的常用方法解決[66-67]。但實際的航天器姿態控制系統是一個復雜的非線性控制系統，線性化的解決方法顯然已不能滿足其需求，因此用非線性控制方法解決航天器姿態控制的問題是目前主流的研究方法，應用較廣的非線性控制方法有基于Lyapunov方法的控制方法、非線性H2/H∞及其混合控制方法、滑模變結構控制方法、自適應控制方法、預測控制方法，以及逆最優控制方法等。由于航天器系統和運行環境的復雜性，需考慮系統的不確定性和工作過程中存在的干擾，文獻[68]將航天器系統的不確定參數與外界干擾的影響統一為總干擾，并通過設計非線性干擾觀測器實現對總干擾的估計，從而保證系統的穩定性。文獻[69]對有大慣量運動部件的三軸穩定衛星在穩態運行期間高精度高穩定度控制方法進行研究，提出了一種動態補償控制算法。

當系統的狀態變量無法由直接測量獲得時，可通過設計系統狀態觀測器或動態補償器的方法，實現輸出反饋控制。文獻[70]針對航天器姿態輸出反饋控制問題，設計了基于模型的二階觀測器。文獻[71]通過在Luenberger觀測器的基礎上加一個變結構控制器設計滑模觀測器以實現系統的穩定控制。設計狀態觀測器實現輸出反饋控制常會使系統復雜化，且狀態觀測器的狀態估計量往往與實際狀態存在偏差。因此，對直接設計輸出反饋的控制方法進行了大量研究。文獻[72]用輸出反饋變結構設計了自適應控制器，可對航天器的未建模動態特性進行控制，并能抑制俯仰軸的振動模態。文獻[73]分析了在狀態不完全可測時帶非線性輸入系統的控制問題，提出了一種輸出反饋變結構控制方法。文獻[74]綜合自適應控制方法與魯棒控制方法設計輸出反饋控制器，僅利用輸出信息實現了航天器的穩定姿態控制。文獻[75]針對姿態調節問題用無源化的方法設計了輸出反饋控制器。

(b)欠驅動姿態控制技術

由于欠驅動模型的獨立控制輸入維數小于自由度維數，使欠驅動航天器的運動特性相對于常見的三軸穩定航天器有較大區別。關于欠驅動航天器最早的理論研究可追溯到1984年[76]。文獻[76]針對剛性航天器在有不同數量的獨立控制輸入力矩的情況下，基于微分幾何理論分別給出了航天器能控的充要條件。文獻[77]指出，若欠驅動航天器僅有2個獨立輸入力矩且輸入力矩與主轉動慣量軸同向，則航天器系統的角速度可漸近穩定的必要條件是欠驅動軸不是系統的對稱軸，并給出了相應的Lyapunov函數。Brockett必要條件指出了欠驅動航天器的姿態控制不可能通過一個光滑定常的靜態或動態反饋控制律漸近穩定到系統的平衡點。即針對兩控制輸入的欠驅動航天器，以往用反饋線性化等能得到光滑控制律的控制方法已不再適用，從而使欠驅動航天器穩定問題變得更復雜。早期針對欠驅動航天器姿態穩定的大部分研究僅以系統的動力學模型為被控對象，即僅考慮系統的角速度變量的穩定性[78]。

目前，針對完整欠驅動航天器系統的閉環姿態穩定問題的研究獲得了一定的進展，主要分為兩大類：不連續定常狀態反饋控制器和連續時變狀態反饋控制器。

對不連續定常穩定控制器，文獻[79]通過采用分段解耦的方式，經過多次分段機動，在有限時間內實現了航天器姿態的穩定，而每次機動均采用形式簡單的PID控制器；文獻[80]進一步發展該方法，在達到相同控制效果的情況下，減少了分段機動的次數。文獻[81]針對非軸對稱情況設計了全局漸近穩定的切換控制器。文獻[82]采用不連續定常的反饋控制器同樣解決了角動量為零的航天器的姿態穩定問題。

連續時變穩定控制器的特點是控制器不僅依賴于系統的狀態，而且依賴于時間變量。連續時變反饋控制器又可分為光滑時變反饋控制器和非光滑時變反饋控制器兩種。光滑時變控制器的控制律光滑，計算便捷，系統穩定性好，易于工程實現；非光滑時變控制器的收斂速度更快，一般能以指數速度收斂。光滑時變穩定控制器的理念最早于1991年提出[83]。在此基礎上，文獻[84]采用中心流形理論，結合平均原理及Lyapunov方法，針對欠驅動航天器，首先設計了光滑時變的局部穩定控制器；隨后文獻[85]提出了非光滑時變控制律，提高了自身算法的收斂速度。

現階段，部分學者對非光滑時變領域進行了研究，而用光滑時變反饋控制解決欠驅動系統的姿態穩定問題已獲得了不少成果。文獻[86]針對任意剪刀對構型飛輪群的欠驅動剛體航天器，用Lyapunov函數方法設計了反饋控制器，實現了系統的姿態穩定。文獻[87]用分層滑模控制方法，根據Lyapunov穩定理論和Barbalat引理，設計了欠驅動航天器的全局穩定姿態控制器；文獻[88]用廣義逆控制理論設計了欠驅動航天器的姿態機動控制器，保證了整個系統的漸近穩定性。

綜上所述：針對剛體衛星，當姿態和角速度信息均可測時，全狀態反饋控制能滿足此類衛星的穩定控制；當僅部分信息能測時，根據可測得的姿態信息采用相應的輸出反饋控制技術；當衛星姿態控制系統呈現欠驅動特性時，將無法得到一般的光滑定常的靜態或動態反饋控制律實現衛星的穩定控制，因此需深入開展滿足此類衛星姿態控制系統漸近穩定控制技術的研究。

b)零動量柔體衛星穩態姿態控制技術

柔性體衛星裝載的柔性結構，使姿態控制設計中需同時考慮整星的姿態穩定與柔性結構的撓性振動干擾抑制。對柔體衛星的姿態控制，根據是否采用分布式執行機構，主要分為集中式姿態控制技術和分布式姿態控制技術。目前，國內外對兩種不同姿態控制方法開展了廣泛研究。

(a)集中式姿態控制技術

對采用集中式姿態控制的柔體航天器，有效載荷與中心剛體固連，姿態控制目標主要是實現中心剛體的精確定向控制；姿態控制執行機構(如動量交換裝置或推力器等)集中安裝于衛星中心剛體上。

對此類航天器姿態控制設計，在分析柔性結構撓性振動特性的基礎上，將姿態控制回路的自然頻率設計為一階固有模態頻率的1/3以下，與柔性結構固有頻率隔離，以同時實現姿態穩定控制和柔性結構撓性振動抑制。但當柔性結構的固有頻率接近姿態控制回路帶寬時，極易激發柔性結構振動，造成系統不穩定[89]。為將柔性結構的狀態變量引入控制系統設計中，從時域的設計角度對基于線性二次型控制理論、滑模變結構控制理論、H∞控制理論、自抗擾控制理論、奇異攝動控制理論、模糊控制理論、神經網絡控制理論等在柔體航天器控制中的應用進行了研究[90-96]。

在用先進控制理論“軟措施”實現柔體航天器姿態控制的基礎上，為進一步提高控制系統穩定性，實現柔性結構撓性振動快速衰減，從能量耗散的角度逐漸發展了多種類型的被動式阻尼器等“硬措施”。能量耗散的要點是將振動能量在結構的局部區域或邊界上損耗掉，耗能方法常被用于控制整個結構的行為[97]。常用的耗能器包括黏滯阻尼器、渦流阻尼器、黏彈性阻尼器、機械摩擦阻尼器、Velcro阻尼器和粉末阻尼器等。被動式阻尼器，無需外界能源和反饋信號，控制簡單，安裝實現易，被廣泛用于工程中，如哈勃太空望遠鏡就在太陽能電池陣驅動機構與展開支架間安裝了一個黏彈性阻尼器，以獲得更好的指向精度[98]。

雖然通過軟-硬結合的姿態集中式控制技術可實現對柔體衛星的穩定控制，但隨著星上柔性結構尺度增大、柔性增強、高精度形面保持要求等問題出現，姿態集中式控制方法的控制效果變得不理想，因此進一步發展了姿態分布式控制技術。

(b)分布式姿態控制技術

當衛星裝載的柔性結構的固有頻率非常低時，不僅模態截斷等造成的建模誤差和撓性干擾等對高精度姿態控制帶來更大的挑戰，而且高性能柔性載荷也對形面精度保持控制進一步提出了苛刻要求，如采用集中式控制方法，將導致控制系統結構十分復雜、控制算法計算量過大，較難實現控制目標。因此，對此類柔體衛星高精度控制，可采用分散姿態控制[99-100]。為滿足對形面保持精度有要求的柔性結構撓性振動主動抑制，提出了在柔性結構上布局傳感器的方法，并結合整星姿態控制提出了分布式控制方案[101]。該方案的核心是柔性結構振動信息的獲取和撓性振動高效主動抑制的實現。

在柔性結構振動信息獲取方面，為全面獲取柔性結構的振動信息，需在柔性結構上安裝傳感器。同時為實現對柔性結構撓性振動的有效抑制，需在柔性結構上安裝作動器。但由于柔性結構本身剛度較低，可安裝傳感器或作動器的位置和數量存在嚴格約束條件，須對傳感器和作動器的布局配置問題進行優化設計。針對該問題，分別從基于Gram矩陣的系統可控/可觀性準則、基于系統能量準則、基于系統響應的配置準則、基于失效和可靠性的配置準則、基于控制/觀測溢出的配置準則、其它準則等多方面進行了研究，形成的成果可實現對傳感器和作動器的優化布局配置[102-108]。針對不同的柔性結構特征，可選擇相匹配的優化準則建立優化目標函數，進而通過一定的優化算法求解出傳感器和作動器的布局配置位置。在確定了傳感器/作動器布局配置位置后，可實現對柔體衛星中柔性結構的撓性振動信息的測量和振動的主動抑制[109]。

在姿態分布式控制技術中，最關鍵的是柔性結構撓性振動主動抑制，最直接的控制方法是速度負反饋控制方法，主要通過在柔性板狀結構同位置測量同位置控制實現，即在正反兩面分別粘貼作動器和敏感器，以構成速度負反饋控制回路[110]。雖然該方法簡單直接，但對多自由度的柔體系統，存在控制溢出問題，較易激發高階模態，造成系統發散。為解決該控制溢出問題，通過將柔體系統動力學方程從物理坐標系轉換至模態坐標系，用正交化的模態坐標描述撓性振動物理變形量，對動力學方程進行解耦，并基于模態方程，提出了“獨立模態控制”方法[111]。該方法是通過將復雜的高階微分方程問題轉為多個低階微分方程問題，達到簡化控制目的。但對復雜柔性結構，由于動力學建模過程中存在模態截斷，采用該方法控制有限階模態時可能激發殘余模態(未控制模態)的振動。為解決殘余模態激發問題，對獨立模態控制方法進行改進，主要通過分析復雜柔性結構模態能量的高低，對系統各階模態由高到低進行排序，先利用m個作動器控制前m階振動模態，降低受控模態能量；然后在控制過程中，監測非受控模態的模態能量，當非受控模態被激發超過前m個受控模態中任何一個模態能量時，作動器轉向作用于這些非受控制模態，抑制其振動，最終實現結構撓性振動的整體受控，該方法為修正的獨立模態控制方法[112]。另外，為解決系統的高頻溢出問題，正位置反饋控制方法(PPF)也被廣泛用于柔性結構振動抑制控制[113]。PPF控制策略針對特定模態，通過閉環極點配置的原理，可大幅提高該模態阻尼而不會引起系統高頻“溢出”問題，對模態頻率的變化也有很好的魯棒性。

上述振動控制方法主要針對柔性結構自身振動抑制進行設計，將柔性結構與整星姿態控制的耦合作用作為外部干擾，雖可實現柔體衛星的穩定控制，但對柔性結構尺寸、重量和轉動慣量等在整星中占比較大的柔體衛星(衛星模態增益系統在0.6以上)，柔性結構與中心剛體耦合作用非常強，采用該控制方法會導致穩定時間長、消耗能量大的問題。為解決上述問題，實現姿態的快速穩定，需對姿態控制與振動抑制控制進行協同設計，即分散協同的控制方法。文獻[114]針對大型柔性結構，將系統分解為多個子系統，在分別設計子系統級H∞狀態反饋器和全局級協同控制器的基礎上，用多級控制方法設計了分散協同H∞控制器，實現了系統的快速穩定。

綜上所述：針對星上柔性結構剛度較大、無形面精度保持要求的柔性衛星，通過采用軟-硬結合的姿態集中式控制技術可實現對此類衛星的穩定控制；對安裝柔性較強且尺度較大柔性結構的衛星，為實現高精度穩定控制或高精度形面保持目標，僅采用姿態集中式控制方法將無法滿足控制目標，須根據此類衛星的結構特性和動力學特性采用相應的姿態分布式控制技術。

1.4.2 單星敏捷機動姿態控制技術

為實現高精度地球立體測繪、自然災害快速響應、軍事偵查衛星快速目標捕獲與追蹤等任務，單個衛星需具備較高的敏捷機動性能。具有敏捷姿態機動能力的衛星通常稱為敏捷衛星，目前成功應用的主要有英國BILSAT-1偵查衛星、美國WorldView系列對地觀測衛星、法國Pleiades光學遙感衛星等，其中姿態角速度機動能力最高可達4.5 (°)/s，姿態角加速度最高2.5 (°)/s2[115-116]。我國的高分二號等對地觀測衛星也具有整星的快速姿態機動能力，具備180 s內實現35°側擺能力。

敏捷衛星姿態機動控制的主要任務是將衛星從一種姿態指向轉換到另一種姿態指向，期間需考慮控制輸入飽和約束、星上載荷及敏感器等角速度約束、冗余星上執行機構控制分配、太陽帆板及柔性天線等結構振動、星敏感器等弱光敏感器對強光源的回避等諸多因素。衛星姿態機動控制系統的敏捷性和精確性等還需權衡系統可靠性、能量消耗的最優性、冗余敏感器及執行器的優化配置與可擴展性等多個因素。根據機動任務過程中的約束形式，姿態控制方法可分為無姿態約束和有姿態約束的姿態機動兩大類。同時，隨著衛星由剛體到柔體的復雜化，姿態機動也會面臨振動控制等更多問題。

a)無姿態約束剛體敏捷衛星姿態機動

對無姿態約束剛體敏捷衛星，主要是實現從當前姿態機動至期望姿態，在機動過程中不考慮天線指向等姿態約束條件。此類衛星的姿態機動控制問題一般可分為開環和閉環兩種模式。開環控制主要是根據期望姿態信息，通過構建最小代價函數，將敏捷機動控制的最優化指令求解問題轉換為一個非線性系統的兩點邊值問題。但開環控制因未實時反饋機動到位偏差，其魯棒性較差，當存在模型誤差或干擾時，會產生較大控制誤差，且對復雜約束問題不易求解，因此較多采用閉環控制模式。閉環控制模式可分為無路徑跟蹤的閉環控制和路徑跟蹤控制。在路徑跟蹤控制策略中，跟蹤控制器的設計與無路徑跟蹤的閉環控制器類似，主要區別是事先需進行機動路徑規劃。以下分別介紹閉環控制方法和姿態路徑規劃方法。

對無路徑跟蹤的閉環控制問題，由歐拉定理可知：空間中任意兩個姿態都能通過繞空間某一固定軸旋轉一定角度相互轉換，因此對三軸姿態機動任務來說，繞空間歐拉軸的旋轉可實現沿最短路徑到達期望姿態。綜合考慮控制系統帶寬、阻尼等因素，文獻[117]提出了一種基于自適應飽和向量的遞階飽和PID控制器，有效結合了傳統頻域分析方法和現代控制方法。考慮剛性衛星的慣量不確定和外部干擾力矩等因素，文獻[118]通過研究冗余飛輪的力矩分配特性，分析姿態機動過程中的最大可行角加速度和角速度，提出了一種基于優化策略的新型制動曲線法，實現了時間高效衛星姿態機動。另外，針對敏捷機動控制問題，對基于其它先進控制方法也進行了廣泛研究，如基于滑模變結構控制的快速姿態機動控制、基于終端滑模的有限時間姿態機動控制、基于反步法的非線性姿態機動控制、基于遺傳算法的飛輪驅動航天器姿態機動控制、基于魯棒控制的姿態機動過程干擾抑制，以及各種考慮執行機構特性的姿態機動控制[119-125]。

在姿態機動路徑規劃方面，各種最優化方法也陸續得到應用。因對剛體衛星，若認為衛星質量特性、執行機構力矩特性等精確已知，不考慮外部隨機干擾和不確定性時，采用最優化方法將有望獲得滿足多種約束的最優姿態機動路徑，然后衛星可采用姿態跟蹤策略實現姿態機動任務。對采用飛輪、控制力矩陀螺等作為執行機構的敏捷衛星來說，時間最優是最具實際應用價值的性能指標。早在1993年，文獻[126]即對剛體航天器的時間最優姿態機動進行了分析，用打靶法獲取了不同角度的時間最優姿態機動路徑，并揭示了不同路徑的時間最優性物理機理。但實際上不同執行機構的力矩約束并不相同，典型的三軸正交安裝的飛輪結構的力矩包絡為正方體，而五棱錐結構的控制力矩陀螺力矩包絡則接近球體，因此文獻[127]根據衛星執行機構力矩的不同約束研究了姿態機動時間最優解的特性。此外，針對以最小冗余度的金字塔構型控制力矩陀螺作為執行機構的衛星時間最優姿態機動，文獻[128]也開展了相關研究。從最優化問題的求解方法來看，目前已有的研究方法包括數值計算方法和非線性規劃方法等[129-130]。近年來，因計算量小、對初值不敏感等特點，偽譜法逐漸被用于解決各種不同的非線性規劃問題。考慮反作用飛輪和控制力矩陀螺等作為執行機構情況，文獻[131]用偽譜法優化獲得了一系列多約束衛星姿態機動路徑。NASA通過離線優化方法獲得了時間最優的姿態機動路徑，并在2010年將其用于太陽過渡區與日冕探測器，首次實現了在軌試驗驗證[132]。

b)復雜姿態約束剛體敏捷衛星姿態機動

敏捷衛星在執行在軌姿態機動任務過程中，除時間最優、能量最優、控制力矩約束和角速度約束等多種約束外，大量實際任務還需考慮弱光敏感器(如星敏感器、紅外和紫外敏感器等)對強光源的回避、合作/非合作目標交會過程中的天線和太陽帆板的避碰等因素產生的禁止姿態約束，或考慮姿態機動過程中太陽帆板指向太陽、通信天線指向中繼站等期望姿態約束等，因此開展復雜姿態約束剛體敏捷衛星姿態機動控制律設計和路徑規劃有其重要的工程應用和理論研究價值。

在閉環控制方面，為實現星上光學載荷對太陽矢量的回避，文獻[133]通過構造和姿態約束相關的勢函數，設計了基于歐拉角的含指向約束衛星大角度姿態機動控制器。類似地，為實現星上安裝的多個星敏感器對太陽矢量的回避，文獻[134]通過構造衛星禁止姿態集合及相關勢函數，設計了基于四元數的含多個指向約束的輪控衛星自主姿態機動控制器。后續研究者也利用羅德里格參數描述禁止姿態并構造勢函數，進而推導姿態機動控制律[135]。由于基于勢函數法設計的控制器在接近禁止姿態時常產生極大的控制力矩需求，遠超出實際衛星控制能力，考慮控制力矩受限情況，對復雜約束衛星姿態機動控制也進行了相關研究[136]。

在考慮多種約束的機動路徑規劃方面，雖然狀態反饋控制規律具計算量小、實時性好等特點，但因僅基于局部狀態信息設計，在控制力矩輸出能力受限時難以確保對禁止姿態的回避，也無法保障姿態機動過程對特定目標的指向，因此較多學者研究了考慮復雜姿態約束的自主姿態機動路徑規劃問題。如基于幾何特征路徑規劃法、考慮約束姿態的約束監測法、隨機姿態規劃法、半定規劃法、粒子算法、偽譜法、對比評估法、基于偽譜法與物理意義結合的混合規劃法等多種方法[137-144]。上述方法雖能解決不同約束下的衛星姿態機動路徑規劃問題，但受制于星載計算機的計算能力約束，只能通過離線路徑規劃與在線軌跡跟蹤結合的方式實現，一定程度降低了敏捷衛星的自主性和快速響應特性。

c)柔體衛星姿態機動控制

當衛星安裝了大型太陽帆板、大型天線等柔性結構，衛星進行快速姿態機動時極易激發柔性結構的撓性振動，進而產生撓性干擾力矩作用于衛星平臺，影響衛星姿態機動的快速性和指向精度。因此，對柔體衛星的姿態機動控制，不僅需滿足機動角度要求以及上述各種約束條件，而且要重點考慮機動快速性和柔性結構的撓性振動抑制問題。

柔體衛星的姿態機動控制包括姿態機動指向控制和撓性振動抑制兩個方面。在姿態機動指向控制中，針對具不確定性的復雜非線性控制問題，目前的解決方案主要有魯棒控制方法、變結構控制方法、自適應控制方法和模糊神經網絡控制方法等[145-149]。在撓性振動抑制中，主動振動控制方法研究成果較多，從原理上可分為兩類策略。一類是調整姿態運動規律，減小對撓性運動的激發，可歸為對姿態控制指令的一種調制，典型方法主要有分力合成、輸入成形等[150-152]。另一類是在柔性結構上配置分布式作動執行機構，通過敏感撓性振動信息直接對柔性結構施加控制作用以抑制撓性振動，典型方法有基于壓電智能材料的主動抑制技術等，此類方法與穩定控制時的主動振動抑制方法相同。

對第一類主動振動控制方法，輸入成形技術是一種時滯濾波技術，以疊加原理為基礎，通過不同相位振動的疊加相消實現振動抑制[153]。在實現中，可通過設計有不同幅值和作用時刻的脈沖序列與系統參考輸入卷積，得到成形后的指令信號。針對傳統零振動輸入成形器對系統模態頻率魯棒性差的問題，后續又提出了零振動零微分(ZVD)成形器、超不敏感(EI)成形器等魯棒成形技術[154]。對多模態系統，還研究了指定不敏感度(SI)輸入成形技術等[155]。其中：針對有柔性附件的航天器，設計了多模態輸入成形器作為前饋結構與閉環控制結合，用于解決柔性附件的振動問題[156-157]。另有部分研究者通過將輸入成形技術與輸出反饋滑模控制、自適應PD復合反饋控制、自適應滑模控制等不同閉環控制方法結合，或將輸入成形技術與機動路徑規劃方法結合，以解決柔性航天器控制中的振動抑制問題[158-161]。但上述輸入成形研究都基于系統的零初始條件假設，對非零初始條件情況就不再適用。目前，國內外針對非零初始條件的輸入成形技術也進行了相關研究[162]。

另一方面，當柔體衛星采用軌跡跟蹤的機動控制策略時，為減小機動過程對撓性振動的激勵，緩解快速性與穩定度的矛盾，合理的規劃機動路徑就顯得愈發重要。剛體衛星快速機動中較常采用的BCB型路徑(即梯形路徑)，因存在角加速度突變，直接用于柔體衛星時易激發振動[163]。針對此問題，目前已提出的解決方案主要有以下幾類。第一類是文獻[164]提出的時間優化-零振動(TO-ZV)路徑規劃方法，通過尋找機動中執行機構的最佳切換時間實現零振動控制。第二類方法是采用較平滑的機動路徑以減小對撓性振動的激勵，包括對Bang-Bang控制的平滑化處理，或采用余弦型、S型速度曲線型、拋物線型等不同路徑形式，并優化路徑參數以減小撓性振動[165-167]。第三類方法是將撓性振動作為性能指標求解最優機動路徑，如文獻[168]針對柔體航天器的rest-to-rest機動，用變分法求解使結構振動最小的最優機動指令；文獻[169]以時間-燃料、撓性振動能量的加權組合為性能指標，采用hp自適應偽譜法規劃了最優機動路徑。另一些路徑規劃研究考慮了系統的柔性特征，如文獻[168]結合系統模態頻率分析了影響結構激勵的機動路徑參數；文獻[170]針對一般的柔性系統給出了基于FIR濾波器的最優時間軌跡規劃方法，同時考慮了時域和頻域約束，可實現對系統殘余振動的抑制。

綜上所述：對無姿態約束的剛體衛星姿態機動問題，目前研究成果較多，多種控制方法均獲得了應用，技術相對較成熟；對有復雜姿態約束的剛體衛星姿態機動問題，在閉環反饋控制中尚需重點考慮控制力矩受限的情況，在路徑跟蹤控制策略中還要進一步提高路徑規劃的自主性與實時性；對柔體衛星的姿態機動控制問題，研究重點是對撓性振動的抑制及撓性振動激勵的減小，目前在輸入成形與路徑規劃上已經進行了大量研究，但仍存在非零初始條件難以應用、計算復雜等問題需解決。

2 多星動力學與控制技術

本章總結了近年來星動力學與控制技術的重點問題。對多星動力學，介紹了相對軌道動力學和姿軌耦合動力學；對多星控制，介紹了位置控制技術及姿軌耦合控制技術近年來的發展。

2.1 多星相對軌道動力學技術

相對運動建模與分析是研究航天器近距離相對運動的理論基礎。通常，相對運動的研究忽略姿態運動，有兩種思路：一是動力學方法，也稱為代數法，以相對運動動力學方程為基礎，便于相對運動制導與控制；二是運動學方法，也稱幾何法，以軌道要素表示的相對運動模型為基礎，便于軌道設計和攝動分析[171-172]。

代數法以兩航天器絕對位置矢量描述的基本運動方程為基礎，通過假設和簡化處理，在相對運動坐標系(Hill坐標系)中建立相對運動模型。C-W方程(也稱為Hill方程或H-C-W方程)是最經典的代數法相對運動模型，它以球形中心引力體和圓參考軌道為假設，未包含攝動力的影響，盡管本身存在誤差，但給出了最簡單的相對運動關系，在編隊飛行、空間交會對接等中應用廣泛。文獻[173]分別分析了地球引力函數的帶諧項(J2項)對C-W方程的影響，并依此改進C-W方程。為解決深空探測日心軌道中探測器與小天體的相對伴飛問題，文獻[174]在同時考慮太陽和小天體引力的基礎上，建立了探測器相對小天體運動的相對動力學方程。

為消除圓參考軌道的限制，文獻[175]假設航天器間距與其地心距的比值為一階小量，通過變量替換，以參考點的真近點角為自變量使方程變為無量綱的形式，將非線性相對運動微分方程組簡化為線性時變方程，即T-H方程，得到二體條件下用真近點角/偏近點角描述的解析解。T-H方程可描述任意偏心率參考軌道的相對運動，但依然存在線性化誤差和攝動誤差。文獻[176]將T-H方程對偏心率作級數展開，分別忽略三階、四階以上的高階項，得到時間顯式解，但僅適于參考軌道偏心率小于0.3的相對運動。文獻[177]以圓軌道交會為背景，給出了無量綱形式的球坐標系相對運動方程的一階解和二階解。

幾何法基于軌道要素描述相對運動，在參考航天器軌道坐標系建立相對運動模型，其精確模型有兩種形式。一是通過坐標轉換，以兩航天器的12個絕對軌道要素為自變量描述[178]。二是利用單位球模型，用參考航天器的絕對軌道要素和追蹤航天器的相對軌道要素描述[179]。這兩種精確模型的本質相同，都是從絕對運動角度建立相對運動模型，適于描述任意偏心率及相對距離的相對運動，但形式復雜不便于揭示相對運動規律。常用的模型是在一定假設條件下的簡化近似模型，依據相對距離可選擇不同階次的近似模型，最常見的是一階近似模型(線性化模型)。

文獻[180]基于現有模型提出了簡化的相對運動模型。文獻[181]基于經典軌道要素分析線性化引起的相對運動誤差，提出了新的相對軌道要素用于衛星編隊飛行構型設計。文獻[182]通過消除密切約束和利用非密切軌道要素得到了用軌道要素差表示的相對運動方程，該模型利于研究一階小擾動對相對軌道動力學的長期影響。文獻[183]采用攝動法解析求得了考慮二階非線性項時橢圓軌道相對運動模型的周期性條件和周期解。

綜上所述：對多星相對軌道動力學技術，通常采用基于相對運動動力學方程的代數法和以軌道要素表示的相對運動模型為基礎的幾何法。代數法常用于相對運動制導與控制，幾何法便于軌道設計和攝動分析。但兩種方法在進行線性化處理時，可能會形成一定的模型誤差，須根據具體的動力學精度要求研究相應的簡化方法。

2.2 多星姿軌耦合動力學技術

在交會對接或在軌服務任務中，最終逼近和停靠段相對位置和姿態通常是強耦合的。傳統上航天器相對運動建模常用姿態與軌道分開描述的方法，軌道參數用位置和速度坐標矢量或軌道六要素描述，而姿態參數采用方向余弦矩陣、歐拉角或四元數等描述。文獻[184]基于軌道坐標系中相對軌道動力學模型和大角度姿態機動控制的姿態動力學模型，通過坐標變換矩陣建立了軌姿耦合數學模型，體現了姿態偏差對軌道運動的影響。文獻[185]基于非線性軌道動力學方程和修正羅德里格斯參數表示的姿態運動方程，建立了六自由度的相對動力學模型，該模型考慮了耦合作用和非線性因素。文獻[186]針對小衛星近距操作過程中姿態和軌道控制問題，建立了小衛星軌道坐標系中相對軌道動力學模型和姿態機動相對姿態動力學模型，并通過期望狀態的設計，建立了姿軌耦合誤差動力學模型。文獻[187]在內編隊衛星系統的全推力器方案設計中，構建了由姿態非線性和共用推力器引起的軌道姿態耦合的六自由度平動和轉動動力學模型。文獻[188]在追蹤航天器本體坐標系中，聯合相對軌道動力學模型和四元數姿態動力學模型，引入推進器配置矩陣，建立六自由度姿態和軌道一體化模型，避免了控制輸入向追蹤器本體坐標系中的轉換。由上述文獻可知：這些動力學建模均是在分別建立相對軌道動力學方程和相對姿態動力學方程的基礎上，實現姿軌耦合誤差動力學建模，但傳統上姿態參數和軌道參數表示的不統一難以實現真正意義的姿軌耦合動力學建模。

部分學者研究了將姿態動力學和軌道動力學用同一參數描述的建模方法，建立了與航天器姿態歐拉動力學方程形式非常相似的軌道動力學方程，為利用成熟的剛體旋轉運動學與動力學研究方法和相關理論進行航天器姿軌一體化研究及分析奠定了理論基礎[189]。在此基礎上，文獻[190]用矢陣(vectrix)方法將航天器姿態運動和軌道運動統一到同一代數框架內，并建立了單個剛性航天器和N個編隊航天器的姿態與軌道耦合動力學模型。文獻[191]推導了基于對偶四元數的剛體航天器平動和轉動組合的跟蹤誤差模型。文獻[192]基于對偶四元數分別推導了交會對接最終段和兩個航天器編隊飛行的六自由度相對運動模型。文獻[193]針對航天器運動姿軌耦合性問題，對基于螺旋理論得到的航天器運動模型，定性分析了近距離復雜操作過程中的姿軌耦合特性，基于對偶四元數獲得了航天器相對運動一體化模型。

綜上所述：傳統航天器姿軌耦合動力學模型中，常用姿態與軌道分別描述的方法，軌道參數用位置和速度坐標矢量或軌道六要素描述，而姿態參數采用方向余弦矩陣、歐拉角或四元數等描述，其耦合性體現在坐標變換矩陣，表示形式不統一，無法實現完全意義的一體化建模，有一定的局限性，而基于對偶四元數和旋量進行姿軌耦合建模的方法可實現姿軌完全一體化建模。

2.3 多星相對位置控制技術

相對軌道控制主要是基于相對測量信息，對航天器質心施加外力，以改變其相對位置和相對速度，稱為相對軌道控制，實現相對位置保持和接近，推力模式分為脈沖推力、連續推力、繼電型推力(有限推力)。相對軌道控制主要包括繞飛控制、接近控制和懸停控制三種控制任務。

相對軌道控制較常用的方法有兩種：一種是基于相對動力學狀態方程的相對控制方法，狀態方程包括C-W方程(僅適于近圓軌道)和T-H方程(可用于橢圓軌道)兩種常用方程；另一種是基于相對軌道要素的相對控制方法。

在基于狀態方程的相對控制方法中，文獻[194]基于離散化的C-W方程設計了一種全狀態的反饋控制器。文獻[195]考慮C-W方程的模型誤差，基于Lyapunov方法設計了編隊衛星相對軌道保持的非線性輸出反饋控制律，該控制律對模型參數不確定性和外界擾動有較強的魯棒性。文獻[196]將J2攝動包含到C-W方程中，得到了平均軌道相對狀態與真實密切軌道相對狀態間的線性化的狀態轉移矩陣，用相平面方法實現相對位置的控制。文獻[197]基于T-H方程分別設計了二脈沖實現繞飛的控制方案和用于編隊衛星構型保持的滑模控制律，使控制方法對攝動干擾、模型不確定等具魯棒性。文獻[198]針對編隊飛行中多個從星飛行任務設計問題，采用偽譜同倫算法對其進行優化，獲得了最優燃料轉移軌道。

在基于相對軌道要素的相對控制方面，文獻[199]針對分布式衛星編隊的構型保持問題，考慮了多種攝動影響，設計了一種基于平均軌道要素的非線性閉環控制方法，該方法具有大范圍穩定性的特點。文獻[200]基于線性化的相對軌道要素方程，采用模型預測控制的方法，得到了編隊構型保持的協同控制算法。文獻[201]針對編隊重構最優燃料消耗控制問題，設計了一種基于平均軌道要素的鄰域最優反饋控制器。文獻[202]針對編隊衛星保持控制問題，基于相對軌道要素方程，采用閉環形式軌道傳遞優化技術規劃脈沖推力序列，實現編隊構型保持。

綜上所述：在多星相對軌道控制中，基于狀態方程的相對控制方法和基于相對軌道要素的控制方法是兩種常用的方法，前者便于相對運動制導與控制的研究，而后者便于定量研究攝動影響和軌道設計。因此，需根據特定任務要求研究適用的控制方法。

2.4 多星姿軌耦合控制技術

航天器相對姿軌耦合控制與相對姿態及相對軌道單獨控制方式不同，它依據航天器整體的運動特性，側重于從系統和全局的角度設計控制器，如空間交會對接終端逼近、在軌服務空間機器人抓捕、多航天器的編隊飛行等。

姿軌耦合控制問題研究前期主要針對穩定目標開展。滑模變結構具魯棒性強的優點，在姿軌耦合控制中有廣泛應用。文獻[184]針對交會對接停靠階段任務，軌道和姿態都采用具滑模的時間次優反饋控制律進行控制。文獻[203]用輸出反饋線性化法解耦編隊航天器非線性的相對軌道和相對姿態動力學模型，然后用滑模控制與神經網絡方法設計控制器。文獻[195]用對偶數描述編隊航天器的相對運動，分別設計了自適應的終端滑模控制器和有限時間控制器。為確保跟蹤誤差全局漸近收斂，文獻[185]基于Lyapunov穩定性理論設計了姿軌耦合的非線性前饋控制律，該控制律具一定的魯棒性。文獻[204]設計了合成控制法，該法包含基于有限時間控制技術的反饋控制和基于非線性擾動觀測技術的前饋補償。文獻[205]對有一個推力器和多個飛輪的編隊航天器相對運動控制問題進行了研究，設計了兩種解耦條件和兩種方法求解期望的姿態，并采用高斯偽譜法將連續控制問題直接轉為離散形式的非線性規劃問題。文獻[187]為實現編隊衛星系統參數不確定條件下的狀態穩定，采用自適應全狀態反饋控制實現內編隊衛星系統的姿態和軌道一體化控制。文獻[206]研究了航天器平動速度和轉動速度不可測的情況，根據位置和姿態信息，用高通濾波估計相對平動速度和轉動速度，設計了非線性的輸出反饋控制律。文獻[207]引入了一種統一的同步結構用于編隊飛行位置和姿態的同步與耦合控制，提出了分散化的跟蹤控制律，通過壓縮分析證明系統的穩定性。文獻[208]針對軌道和姿態耦合時從星對主星軌跡的跟蹤控制問題，設計了全局收斂的自適應控制器。

目前姿軌耦合控制主要集中于對失效翻滾目標特定部位的接近和停靠任務研究。文獻[209]針對翻滾目標的接近機動問題，設計了滑模控制器和基于狀態相關黎卡提方程控制器(SDRE)以解決非線性的六自由度控制問題。文獻[210]針對翻滾目標接近的非線性相對位姿耦合控制問題，基于滾動優化設計了theta-D次優控制器，通過攝動法求得HJB方程的近似解，實現相對運動的姿軌協同控制，在跟蹤期望軌跡實現臨近懸停的同時還跟蹤了目標的姿態。文獻[211]提出一種面向對旋轉目標空間操作的安全可靠的逼近策略及相應的控制方法，設計了基于退步控制理論的姿軌耦合退步控制器。文獻[212]針對無控旋轉目標的逼近問題，采用滑模變結構的控制方法，實現同步逼近相對運動參考軌跡和參考姿態。文獻[213]針對大空間目標捕獲和移除任務，提出用自適應滑模控制方法控制航天器的姿態和軌道，該方法能較好地解決參數不確定和外干擾的問題。文獻[214]針對旋轉目標的抓捕任務需求，利用面內相對運動軌跡的凸逼近特性，提出了飛越制導控制策略。文獻[215]研究了自由飛行航天器和空間懸浮目標的運動同步問題，考慮重力梯度和其它未知但有界的干擾引起的干擾力矩，分別基于自適應控制理論和自適應反饋線性化方法設計了相對軌道和相對姿態的跟蹤控制律，以保證追蹤航天器與目標航天器間的相對位置矢量始終指向目標航天器對接口。針對自由翻滾目標接近過程的最優控制，文獻[216]考慮了一個受限平面剛體運動，設計了一個接近翻滾衛星的前饋最優控制策略，實現了最小化時間/最優燃料消耗控制。文獻[217]針對自由翻滾航天器的近距離最優交會問題，分別提供了一種用直接法-高斯偽譜法和虛擬域逆動力學法解決翻滾目標接觸點逼近問題。

綜上所述：對多星姿軌耦合控制問題，已從穩定目標的逼近抓捕任務轉向失效旋轉或翻滾目標的接近停靠任務，目前的逼近導引規劃及控制主要針對合作目標開展了相應的理論研究；對非合作目標任務，綜合最優方法的研究和在軌應用尚存在較大差距。特別是在翻滾目標的接近停靠任務中，由于翻滾目標接近停靠過程中的非線性特性和參數不確定性等因素，需深入對強魯棒性自適應控制方法進行研究。

3 新型航天器動力學與控制技術

本章介紹了太陽帆航天器和繩系衛星兩種新型航天器目前的在軌任務情況及其動力學與控制技術的研究現狀。

3.1 太陽帆航天器

3.1.1 太陽帆航天器在軌任務

太陽帆帆面一般由厚2 μm的高反射薄膜構成，大尺寸帆面在軌展開后可通過捕獲太陽光通量獲得連續小推力。與傳統航天器相比，太陽帆毫牛量級的連續光壓力可突破任務設計時的燃料約束考慮，有廣闊的應用前景。隨著科技水平的進步，太陽帆航天器研究逐漸從理論走向了工程實際。1999年，世界第一個太陽帆航天器地面展開試驗由歐空局(ESA)與德國宇航局(DLR)共同設計實現，設計的正方形太陽帆邊長20 m，地面試驗現場如圖3所示[218-219]。之后NASA的Nano Sail-D太陽帆、Lightsail-1和Lightsail-2太陽帆相繼問世，其中Lightsail-2太陽帆的任務目標是保持在日地系統平動點附近周期軌道以實現對太陽風暴的提前觀測[220-221]。2010年，日本IKAROS太陽帆由日本宇航局JAXA成功發射，在世界上第一次實現了在軌光壓加速飛掠火星，IKAROS太陽帆在軌實物如圖4所示[222]。設計為正方形邊長14 m的IKAROS太陽帆航天器成功獲得了1.12 mN的光壓力并在軌驗證了其姿態軌道控制能力。IKAROS太陽帆的成功是太陽帆航天器技術的重大突破，顯著推動了太陽帆航天器技術的研究及其在深空探測領域的工程應用。

3.1.2 太陽帆航天器姿態動力學與控制

太陽帆姿態控制是太陽帆航天器工程應用的前提，有重要的現實意義和理論價值。相較傳統航天器，太陽帆航天器姿態控制的難點是其大尺寸薄膜帆面的存在導致其具顯著的柔性特征，姿態調整和柔性結構振動會導致推力大小、方向發生改變，進而影響航天器的軌道機動[223]。因此，必須研究太陽帆柔性結構(大尺寸薄膜帆面和大尺度柔性桿)與姿態動力學的耦合關系和交互作用，并建立能反映太陽帆本質特征的剛柔耦合動力學模型，在此模型基礎上設計能同時實現姿態鎮定和柔性結構振動抑制的控制策略。

目前，已有的太陽帆航天器姿態動力學與控制研究多假設其為剛性結構，忽略或回避了其難以解決的柔性特征。普遍使用的太陽帆行航天器結構有兩種：分別為DLR提出的萬向節控制結構和美國噴氣實驗室(JPL)提出的小帆控制結構。已有研究者分析了太陽帆的光壓與推力的函數關系，目前由MCINNES提出并已普遍應用的表達式只能適用于太陽帆航天器的平面模型[224]。文獻[225]針對兩種太陽帆航天器結構，提出了太陽輻射光壓力模型和剛體動力學模型。文獻[226]提出了太陽帆在光壓作用下所有力和力矩的解析函數的一般模型。

已有的基于剛性模型的太陽帆姿態控制器設計方法包括自旋鎮定、推力矢量控制、移動/傾斜帆面控制、變反射率控制等。但這些方法均未考慮太陽帆柔性持征。文獻[223]在文獻[225]剛體姿態動力學模型的基礎上，考慮太陽帆的柔性特征，提出了具有剛柔耦合特征的非線性姿態動力學模型，并設計了LPV姿態控制器同時滿足了姿態角鎮定以及柔性模型的振動抑制，但并未考慮控制器輸出飽和約束。因此，太陽帆姿態控制器設計難點集中表現在模型的非線性、需同時考慮姿態控制輸出飽和約束，以及帆面柔性模態的振動抑制。

3.1.3 太陽帆航天器軌道動力學與控制

近年來，文獻[67，227-228]對太陽帆軌道動力學進行了大量基礎性研究，完成了太陽帆航天器不同任務的軌道動力學分析與設計。文獻[219]計算并提出日地系統中太陽帆光壓力可產生人工平動點，且可通過改變帆的結構以調整光壓力的大小實現空間大范圍的平動點重置。太陽帆航天器圓型限制性三體下，滿足一定初始狀態仍可獲得條件穩定的Lissajous軌道和Halo軌道[67]。因為這些軌道的不穩定特征，在完成平動點軌道射入后須施加保持控制以防止航天器軌道發散。與傳統航天器軌控不同，太陽帆航天器軌道控制是通過調整姿態角、帆面面積或帆面反射率改變光壓力而間接實現的。

文獻[229]在Hill模型中用基于近似化處理方法通過控制帆面姿態角和帆面面積設計實現了太陽帆航天器最優軌道控制器。文獻[230]對太陽帆航天器懸浮軌道和平動點軌道動力學進行了研究，并設計了太陽帆航天器被動穩定控制，針對兩帆結構的太陽帆航天器提出了反饋線性化控制律設計方法，通過調整姿態角實現軌道控制。文獻[231]考慮近似化獲得的線性時變系統設計了太陽帆軌道最優控制器，但控制器參數需通過不斷求解時變系統的Riccati方程獲得。文獻[232]對姿態角幅值約束下的太陽帆航天器軌道控制問題進行了研究，設計了軌道保持最優控制器。文獻[233]分析了太陽帆航天器Halo軌道的不穩定特性，采用離散尋優方法通過調整姿態角抑制軌道發散趨勢，使太陽帆航天器保持在一類Halo族上。文獻[234]為使太陽帆行星捕獲終端軌道要素同時滿足目標工作軌道的要求，提出了一種分段捕獲策略及相應的聯合解析最優控制律。太陽帆航天器軌道控制問題屬于典型的強耦合非仿射非線性系統穩定問題，近似線性化方法本質上存在近似模型有效性問題和控制器收斂問題，且一般很難求出吸引區。近年來，部分直接處理非線性系統控制問題的先進控制器被引入太陽帆軌道控制。文獻[235-236]提出了高階非線性滑模控制器用以解決日地L2點平動點軌道上太陽帆航天器編隊飛行控制任務，進一步將變結構模型參考自適應控制方法成功引入太陽帆航天器平動點軌道控制和編隊飛行中，-定程度解決了太陽帆航天器平動點軌道穩定控制問題。

綜上所述：太陽帆航天器可實現無推進劑推進，將深空探測器推進到太陽系深處，使探測器脫離黃道面到達太陽極軌進行對日觀測，進入懸浮軌道等常規航天器難以實現，同時又有重大科學意義的非開普勒軌道，具廣闊的應用前景。相較國外，我國的太陽帆航天器研究起步較晚，基礎理論研究相對薄弱。目前對柔性太陽帆的控制大部分僅考慮姿軌耦合動力學建模與控制，當太陽帆的柔性對任務產生較大影響時，需進一步研究對其結構振動的控制，以及對太陽帆軌道-姿態-振動的耦合動力學建模與控制技術。太陽帆航天器軌道動力學與控制是太陽帆應用的關鍵技術之一，著眼我國太陽帆的發展需要及平動點軌道任務的實際需求，開展太陽帆航天器軌道動力學與控制技術研究有重要意義。

3.2 繩系衛星

繩系衛星系統動力學及控制問題亦非常復雜，當它被置于空間環境并與衛星耦合時極易產生一系列復雜的天平動及振動[237]。本節主要對二體繩系衛星系統和繩系衛星編隊在釋放、回收、平衡控制各個階段的動力學特性，主要包括運動形式和主要影響因素、動力學建模、控制規律設計以及仿真分析等進行總結，為后續繩系衛星任務提供參考。

3.2.1 繩系衛星系統在軌任務

鑒于空間繩系衛星輕便、節能及可重復使用等特點，美國NASA、意大利航天局(ASI)、加拿大航天局(CSA)、美國海軍研究實驗室(NRL)、日本宇宙科學研究所(ISAS)和ESA等研究機構已進行了數十次繩系衛星在軌試驗，結果見表1[238]。其中：TSS-1R，SEDS-1系統分別如圖5、6所示。這些試驗為擴大空間繩系技術的應用做出了巨大貢獻，部分關鍵技術得以突破，甚至發現了未曾預料的科學結果。如系繩釋放及回收技術、系繩切斷、航天器再入、電動力學及繩系在軌生存能力等。由于繩系衛星系統是高度非線性的動力學系統，加之釋放機構設計、在軌飛行環境的不確定性等因素，導致有數次任務未取得預期效果，這一定程度限制了繩系技術的應用。

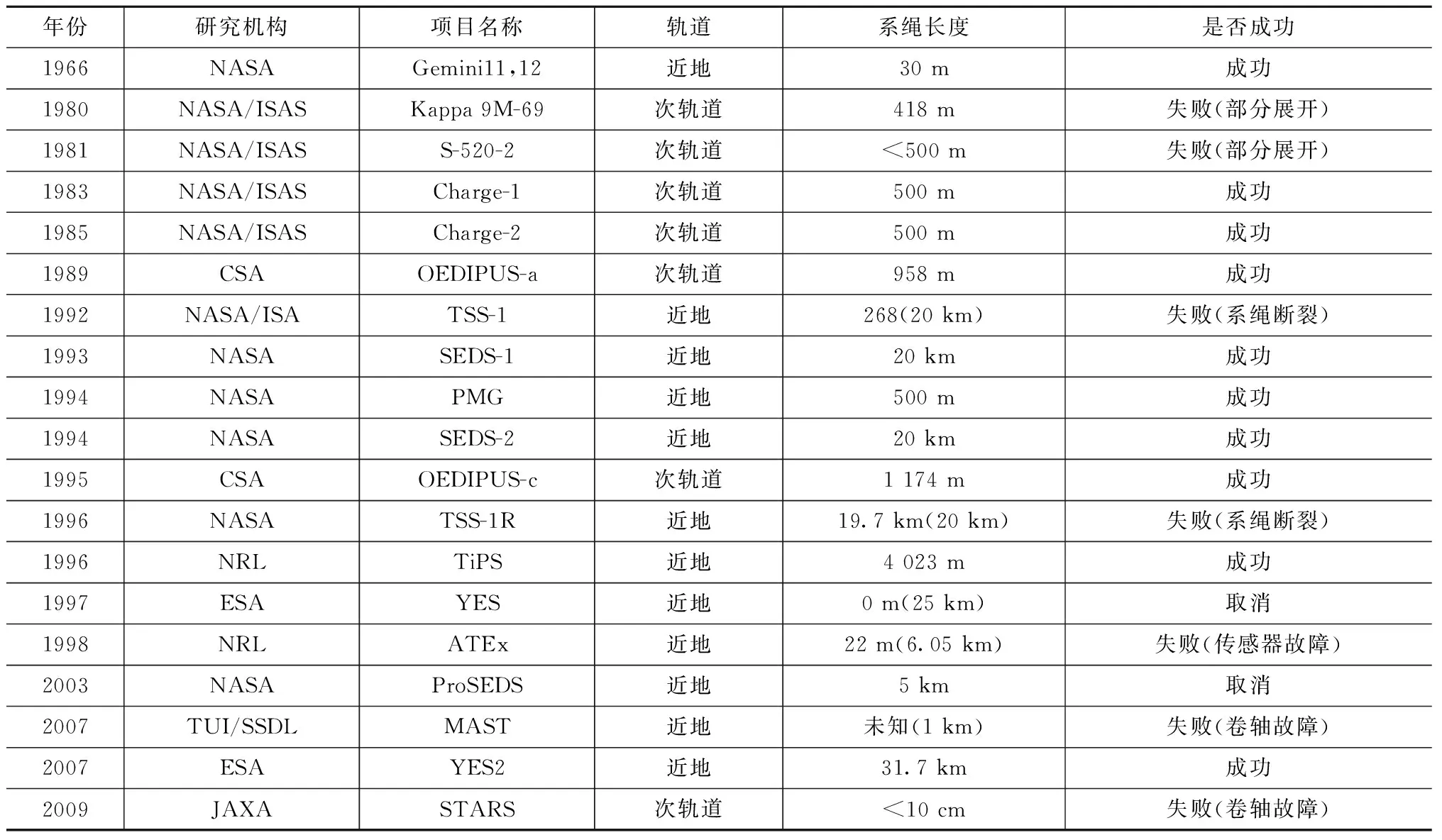
表1 歷年繩系衛星系統在軌試驗Tab.1 On-orbit experiments of tethered satellite system

3.2.2 二體繩系衛星動力學與控制

現有對繩系衛星系統的理論研究中，大多采用將衛星簡化為質點，系繩簡化為剛性桿的低自由度模型進行分析。文獻[239]系統研究了兩體繩系衛星系統建模、動力學與控制問題，分析了衛星的釋放控制、相對平衡位置穩定性及系統混沌動力學。文獻[240]對電動力繩系衛星系統進行了研究，分析了電動力能量輸入所造成的不穩定因素，用漸近分析及數值方法分析了系統的周期運動，提出兩種反饋控制算法并進行了評估。文獻[241]針對電動力繩系衛星系統設計了混合控制策略，通過電動力和移動系繩系釋放點抑制不穩定的高階模態。文獻[242]基于軌道面內的剛性系繩模型，通過反饋控制將電動力繩系衛星系統由一個平衡位置轉移到另一個平衡位置。文獻[243]對地磁場、系繩動力學、重力及電動力進行了建模，并分析了電動力作用對繩系衛星軌道要素的長期影響。文獻[244]研究了系繩回收階段二體繩系衛星系統的運動過程，設計了一個非線性控制律降低了系繩回收階段振動幅值。文獻[245]對繩系衛星系統在系繩指數展開率下的運動進行了分析，認為將繩系衛星沿垂直方向排列可能會避免后期振動。文獻[246]考慮面內與面外的三維系繩展開控制問題，設計一種線性的拉力控制律達到了穩定。文獻[247]采用截斷Chebyshev級數估計系統狀態變量，針對三維繩系子衛星系統的展開和回收設計了最優控制器。文獻[248]研究了繩系近距離快速釋放問題，提出了以一定初始速度釋放子星并通過減速釋放的方法。文獻[249]對二體繩系衛星系統的子星回收過程中的非線性后退時域控制問題進行了研究，通過調節系繩張力和作用于子星的力矩實現了子星的穩定回收控制。文獻[250]采用簡單張力控制策略使其對圓軌道和近圓軌道繩系衛星系統的釋放、滯留和回收過程都有較好的適應性。文獻[251]研究了繩系衛星在軌運動中系繩參數的實時估計方法。

很多系繩衛星系統應用中，假設系繩為剛性繩與實際情況有較大出入，對系統的動力學建模與分析也不夠精確，因此研究者開始對柔性系繩模型進行建模與分析。文獻[252]考慮具有分布質量的柔性系繩模型，提出一種距離速率控制算法。文獻[253]對上述模型進行改進，考慮系統面外運動，研究了電動力繩系衛星系統的平衡控制問題。文獻[254]針對軌道面內的柔性系繩模型，設計反饋控制律將電動力繩系衛星系統由一個平衡位置轉移到另一個平衡位置。文獻[255]考慮了系繩的黏彈性、分布質量和空間位形，建立一種改進珠式模型描述了系繩的縱橫向振動。文獻[256]針對無限維的黏彈性二體繩系衛星系統提出了時變動力學模型。文獻[257]針對繩系衛星的展開控制設計了數種控制器，基于黏彈性空間臺球模型，利用系統的混亂特性，相較傳統控制方法可使系統更快到達平衡狀態。

3.2.3 繩系衛星編隊動力學與控制

繩系衛星編隊動力學與控制是一個相對較新的研究領域。繩系編隊飛行系統相對無系繩編隊系統的主要優勢是：該種系統可通過調整系繩張力保持或改變隊形，從而降低燃料消耗。現有理論研究多采用將繩系衛星簡化為質點，系繩簡化為剛性桿的低自由度模型進行分析。繩系衛星編隊可有多種構型，大量研究者對不同構型的繩系衛星編隊動力學進行了穩定性分析并得到了穩定構型。文獻[258]借鑒圓軌道上軸對稱旋轉剛體的三類平衡態，研究了平面旋轉繩系衛星編隊系統的穩定性問題，并對一種面向地球的三維雙四面體繩系衛星編隊飛行系統進行了穩定性分析。文獻[259]分別對面向地球的環狀和三維雙金字塔構型的繩系編隊系統進行了動力學分析。文獻[260]考慮系統旋轉平面位于軌道面內及垂直于軌道面兩種情況，研究了輻式繩系衛星編隊飛行系統的動力學與穩定性問題，并將其研究結果擴展到三維雙金字塔構型。文獻[261]研究了橢圓軌道上三角形繩系衛星編隊系統，得出了系統參數的平衡設計閾值，分析了系繩釋放及回收對系統響應的影響。文獻[262]在三體系統的平衡構型基礎上，用延續算法確定了軌道平面內線形四體繩系編隊系統的多種平衡構型。文獻[263]研究了由三根無質量剛性桿連接的四體繩系衛星模型，并分析了兩類四面體形的系統平衡構型。

在此基礎上，研究者針對繩系衛星編隊穩定構型討論了構型保持或變換控制。文獻[264]采用攝動法研究了線形繩系衛星編隊系統的姿態動力學，提出通過一對電推進器改變系統旋轉平面并設計了相應的開環控制律。針對空間科學任務SPECS(Submillimeter Probe of the Evolution of Cosmic Structures)需求，文獻[265]研究了平面三角形繩系衛星編隊飛行系統動力學，采用輸入-狀態反饋線性化方法設計了非線性跟蹤控制器。文獻[266]對已有的時滯反饋控制方法進行改進，與模型跟蹤、模型解耦控制方法結合控制直連式三體繩系衛星編隊系統的擺動。文獻[267]隨后將研究范圍擴展到雙金字塔型繩系衛星編隊系統，通過改變系繩中電流控制系繩的擺動。文獻[268]考慮軌道面內三角形旋轉繩系衛星系統的最優控制問題，采用直接轉換法分別對最短時間重定向、衛星釋放及衛星回收三種不同任務設計了最優張力控制律和狀態軌道。文獻[269]研究了旋轉繩系衛星編隊系統的“圓形”運動及隊形相似變換，得出相應的平衡條件，并將系繩收放機構、機械臂、推進器及反作用動量輪作為執行機構設計了協調控制律。文獻[270]進一步考慮繩系衛星的姿態運動，基于同步思想的模型縮減方法對多體旋轉繩系衛星編隊系統動力學進行簡化并設計了非線性魯棒及自適應算法，進一步研究了只采用飛輪作為執行機構的欠驅動系統的控制問題。文獻[271]用拉格朗日方法對直連式三體繩系衛星進行了動力學建模，分別針對集中和分散的動力學模型設計了二次型最優調節器。

文獻研究表明：繩系衛星系統(包括動量交換繩系和電動力繩系)可實現無推進劑推進，提供各種離軌和再入功能，有廣闊的應用前景。動力學與控制是空間繩系研究的兩個重要內容，在當前研究中，多將系繩末端物體視為點質量，且不考慮系繩末端物體繞質心運動對系統動力學的影響。由于其復雜性，目前對弱張力繩系系統的研究非常罕見，弱張力繩系系統的運動較現模型假設更為復雜，起旋、展開回收時殘余張力及各種外部攝動力和內部非線性因素都會明顯影響系繩的運動。同時，關于多體繩系系統動力學的研究較少，對繩系系統的混沌運動幾乎沒有研究，這種運動會導致出現諸多不良影響。由于繩系具強非線性且運動過程中存在復雜的多場耦合問題，建立精確動力學模型并采用合適的控制策略成為亟待解決的問題。

4 結束語

本文綜述了空間飛行器動力學與控制多方面的研究進展。目前空間飛行器的結構和功能越來復雜，逐漸向深空探測、單顆大型多功能的復雜構型衛星、多顆衛星編隊和新型航天器等方向發展，由此激發了關于空間飛行器的動力學與控制在各領域研究的深入，研究范圍涵蓋了軌道動力學、姿態動力學、姿態控制和編隊控制等領域。隨著研究的深入，出現了以下新的研究重點及主要發展方向。

第一是深空探測的軌道動力學問題。對小行星探測或星際航行任務，由于空間飛行器在飛行過程中受到多天體的引力影響，后續需對橢圓軌道類型的三體問題進行深入研究。目前在該方面，國外針對日地平動點進行了大量研究，并在共線平動點附近開展了多個探測任務；國內研究主要針對地月L1和L2平動點，包括中心流形的各類軌道，其中嫦娥2號衛星進入了地月L2點的Lissajous軌道；后續研究需將其推廣到更遠的深空，特別是小天體任務中的平動點軌道研究。

第二是超大尺度柔性航天器的動力學建模與協同控制技術。由于超大尺度柔性航天器的柔性載荷需要在軌多次展開，結構中包含眾多間隙旋轉鉸，且在軌飛行時受復雜外部環境影響，使間隙碰撞-柔體彈性-外部環境三者相互耦合，導致精確的動力學模型建立困難。同時，為保證柔性載荷的功能和性能，對柔性載荷的形面精度控制也提出了較高要求。在控制系統設計過程中，需同時考慮姿態指向控制和柔性載荷的形面保持控制，其實現更為困難和復雜。目前，在該方面國內外針對太陽翼或桁架結構等開展了動力學建模技術研究和撓性振動主動抑制技術研究，但研究成果較多集中于針對特定研究對象或基于理想假設的數值仿真研究。因此，后續需在超大尺度柔性航天器的在軌動力學建模技術和分布協同控制技術方面進行深入研究。

第三是敏捷衛星的機動控制技術。由于敏捷衛星的機動速度越來快、機動角度越來越大，并且存在飛行任務的不斷切換，造成路徑規劃實時性要求更高，考慮的約束因素更多。同時，需解決姿態機動的快速性與高穩定度間的矛盾。目前，在該方面國內外針對剛、柔體衛星的快速機動快速穩定技術進行了大量理論與應用的探索，但受限于大角度機動與振動控制問題本身的復雜性，所適用的機動任務依然相對較簡單，在技術與應用中仍有較大的探索空間。因此，后續需對多約束條件下的姿態路徑規劃技術、非零初始條件下的輸入成型技術等進行深入研究。

第四是多星姿軌耦合動力學和控制技術。在多星在軌耦合動力學和控制技術中，對翻滾目標接近停靠過程中的動力學建模和控制面臨巨大的困難，主要是由于翻滾目標的旋轉和章動特性，再加上天線、帆板等附件的耦合運動，導致目標的動力學特性異常復雜。目前，國內外針對翻滾目標接近過程中的耦合動力學建模和控制問題開展了大量研究，但研究成果較多集中在基于理想假設的數值仿真研究。因此，后續需在翻滾目標捕獲過程中姿軌耦合動力學建模和姿軌耦合控制方面開展深入研究。

第五是太陽帆航天器動力學與控制技術。太陽帆航天器存在軌道與姿態強耦合、柔性太陽帆復雜形變與振動問題，后續需在全柔性太陽帆航天器姿態軌道振動耦合動力學建模技術、拉格朗日點附近編隊控制技術、引力拖車控制技術、日心懸浮軌道設計與控制技術、太陽帆逃逸地球軌道最優控制技術、太陽帆轉移軌道最優控制技術、太陽帆與其它航天器的碰撞風險和提高太陽帆生存能力等方面進行深入研究。

第六是空間繩系衛星系統的動力學與控制技術。對空間繩系衛星，由于繩系具強非線性且運動過程中存在復雜的多場耦合問題，建立精確動力學模型設計控制律較難，后續需要考慮系繩連接體相互作用情況下，研究系繩連接體相對質心的運動；并對弱張力繩系系統進行研究，尋求一種精確、簡單且可靠的控制系統；同時研究展開機構對系統的攝動影響，以及對混沌發生情況的預估和尋找消除混沌現象的手段。為將繩系系統理論用于實際任務，需在繩系衛星系統設計、繩系衛星動力學建模及控制、繩系衛星系統的安全操作、繩系衛星展開與回收方法、繩系衛星交會對接技術、地面演示試驗與研究、繩系衛星與其它航天器的碰撞風險、提高繩系衛星系統生存能力和繩系衛星性能最優控制等方面進行深入研究。

[1] 劉林. 航天器軌道理論[M]. 北京: 國防工業出版社, 2000.

[2] 童科偉, 周建平, 何麟書. 近地衛星簡化軌道預報方法研究[J]. 宇航學報, 2009, 30(4): 1327-1333.

[3] 劉林, 胡松杰, 王歆. 航天動力學引論[M]. 南京: 南京大學出版社, 2006: 204-230.

[4] YOSHIKAWA M, IKEDA H, YANO H, et al. Astrodynamics science about Itokawa, gravity and ephemeris[R]. AIAA, 2006-6658, 2006.

[5] WERNER R A. SCHEERES D J. Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4 769 castalia[J]. Celestial Mechanics and Dynamical Astronomy, 1997, 65: 313-344.

[6] 崔平遠, 喬棟. 小天體附近軌道動力學與控制研究現狀與展望[J]. 力學進展, 2013, 43(5): 526-539.

[7] 李四平, 劉錦陽, 國鳳林, 等. 軌道機動的時間-能量綜合最優控制[J]. 宇航學報, 2010, 31(1): 137-142.

[8] 趙堅. 太陽同步(準)回歸軌道衛星的軌道保持方法研究[J]. 中國空間科學技術, 2004, 24(4): 60-64.

[9] 李果. 同步軌道多星共位軌道保持技術研究[J]. 航天控制, 1997, 23(3): 73-80.

[10] 王信峰, 李言俊, 侯黎強. 基于Hill方程近地衛星模型預測軌道保持方法[J]. 系統仿真學報, 2008, 20(22): 6273-6277.

[11] 韓潮, 付紅勛. 軌道維持與機動的最優控制[J]. 航天控制, 2000, 26(4): 40-46.

[12] FERNANDO A. 2011 Mars science laboratory mission design overview[J]. Earth & Space, 2010, 170(366): 873-897.

[13] 張曉文, 王大軼, 黃翔宇. 深空探測轉移軌道自主中途修正方法研究[J]. 空間控制技術與應用, 2009, 35(4): 27-33.

[14] RAYMAN M D, VARGHESE P, LEHMAN D H, et al. Results from the Deep Space 1 technology validation mission[J]. Acta Astronautica, 2000, 9: 475-487.

[15] KUNINAKA H, KAWAGUCHI J I. Deep space flight of Hayabusa Asteroid Explorer[J]. Space Exploration Technologies, 2008, 6960: 1-10.

[16] LONDON H S. Change of satellite orbit plane by aerodynamic maneuvering[J]. Journal of the Aerospace Sciences, 1962, 29: 323-332.

[17] BRAUN R D, MANNING R M. Mars exploration entry, descent, and landing challenges[J]. Journal of Spacecraft and Rockets, 2007, 44(2): 310-323.

[18] LI S, JIANG X Q. Review and prospect of guidance and control for Mars atmospheric entry[J]. Progress in Aerospace Sciences, 2014, 69: 40-57.

[19] SAN MARTIN A M, WONG E C, LEE S W. The development of the MSL guidance, navigation, and control system for entry, descent, and landing[C]// 23rd AAS/AIAA Space Flight Mechanics Meeting. Kauai: AAS, 2013: 13-238.

[20] PRAKASH R, BURKHART P D, CHEN A, et al. Mars science laboratory entry, descent, and landing system overview[C]// Aerospace Conference. Montana: IEEE, 2008: 1-18.

[21] CHEN A, GRECO M, MARTIN-MUR T, et al. Approach and entry, descent, and landing operations for the Mars science laboratory mission[C]// 23rd AAS/AIAA Space Flight Mechanics Meeting. Kauai: AAS, 2013: 13-425.

[22] 孫澤洲, 賈陽, 張熇. 嫦娥三號探測器技術進步與推動[J]. 中國科學: 技術科學, 2013, 43(11): 1186-1192.

[23] 王大軼, 李鐵壽, 馬興瑞. 月球探測器重力轉彎軟著陸的最優制導[J]. 自動化學報, 2002, 28(3): 385-390.

[24] 雷漢倫. 平動點、不變流形及低能軌道[D]. 南京: 南京大學, 2015.

[25] CANALIAS E, GOMEZ G, MARCOTE M, et al. Assessment of mission design including utilization of libration points and weak stability boundaries[D]. Barcellona: Universitat de Barcellona, 2004.

[26] 劉俊澤, 徐紅兵, 崔雁. 嫦娥二號衛星飛日地L2點的軌道設計與實施: 中國宇航學會深空探測技術專業委員會第十屆學術年會[C]// [S. l.]: 2013.

[27] 曲廣吉, 程道生. 復合柔性結構航天器動力學模型的混合坐標法建模研究[J]. 航天器工程, 1998, 9(3): 33-38.

[28] 朱明. 奇異值分解(SVD)在多體系統動力學中的應用——對R/W體系的補充[J]. 力學季刊, 1987(4): 24-32.

[29] 茍興宇, 馬興瑞, 王本利. 航天器動力學研究內容的層次結構[J]. 航天器工程, 2000, 9(1): 4-14.

[30] BALL R S. A treatise on the theory of screws[M]. Cambridge: Cambridge University Press, 1900.

[31] KANE T R, LEVINSON D A. The use of Kane’s dynamical equations in robotics[J]. International Journal of Robotics Research, 1983, 2(3): 3-21.

[32] RODRIGUEZ G, JAIN A, KREUTZ K. Spatial operator algebra for multibodysystem dynamics[J]. The Journal of the Astronautical Sciences, 1992, 40: 27-50.

[33] 孟占峰, 韓潮. 基于空間算子代數的航天器多體動力學遞推實時仿真算法[J]. 航空學報, 2007, 28(S1): 49-56.

[34] 洪嘉振, 梁敏. 多剛體內碰撞數學模型及計算程序[J]. 力學學報, 1989, 21(4): 509-512.

[35] LIU J Y, LU H. Rigid-flexible coupling dynamics of three-dimensional hub-beams system[J]. Multibody System Dynamics, 2007, 18: 487-510.

[36] WINFREY R C. Elastic link mechanism dynamics[J]. ASME Journal of Engineering for Industry, 1971, 93: 268-272.

[37] KIM S S, HAUG E J. A recursive formulation for flexible multibody dynamics, part 2: closed-loop systems[J]. Computer Methods in Applied Mechanics and Engineering, 1989, 74: 251-269.

[38] PASCAL M. Some open problems in dynamic analysis of flexible multibody systems[J]. Multibody System Dynamics, 2001, 5: 315-334.

[39] MEIROVITCH L. Hybrid state equations of motion for flexible bodies in terms of quasi-coordinates[J]. Journal of Guidance, Control, and Dynamics, 1990, 14(5): 1008-1013.

[40] MODI V J. Attitude dynamics of sateiiltes with flexible appendages, a brief review[J]. Journal Spacecraft and Rocket, 1974, 11(11): 743-751.

[41] 劉延柱. 航天器姿態動力學[M]. 北京: 國防工業出版社, 1995.

[42] 黃文虎, 邵成勛. 多柔體系統動力學[M]. 北京: 科學出版社, 1996.

[43] NEWMARK N M. A method of computation for structural dynamics[J]. ASCE Journal of the Engineeing Mechanics Division, 1959, 85(3): 67-94.

[44] BATHE K J, WILSON E L. Numerical methods in finite element analysis[M]. Englewood: Printice-Hall, 1976.

[45] ASCHER U M, PETZOLD L R. Computer methods for ordinary differential equations and differential algebric equations[M]. Beijing: Science Press, 2009.

[46] 吳志橋. 非慣性系下柔性結構動力學研究[D]. 長沙: 國防科學技術大學, 2004.

[47] 吳鋒, 高強, 鐘萬勰. 剛-柔體動力學方程的保辛攝動迭代法[J]. 應用數學和力學, 2014, 35(4): 341-352.

[48] HSIAO K M, YANG R T, LEE A C. A consistent finite element formulation for non-linear dynamic analysis of planar beam[J]. International Journal for Numerical Methods in Engineering, 1994, 37: 75-89.

[49] LWOEN G G, CHASSAPIS C C. The elastic behaviour of linkages[J]. Mechanism and Machine Theory, 1986, 21: 33-42.

[50] THOMPOSN B S, SUNG C K. A suvery of finite element techniques of mechanism design[J]. Mechanism and Machine Theory, 1986, 21(4): 351-359.

[51] WALLRAPP O, SCHWERTASSEK R. Representation of geometric stiffening in multibody system simulation[J]. International Journal for Numerical Methods in Engineering, 1991, 32: 1833-1850.

[52] ZHANG D J, HUSTON R L. On dynamic stiffening of flexible bodies having high angular velocity[J]. Mech Struct & Mach, 1996, 24(3): 313-329.

[53] LIU A Q, LIEW K M. Non-linear substructure approach for dynamic analysis of rigid-flexible multibody systems[J]. Computer Methods in Applied Mechanics and Engineering, 1994, 114: 79-396.

[54] 劉又午, 王樹新， 王建明， 等. 復雜結構航天器的柔性多體動力學分析[J]. 航天器工程, 1998, 7(3): 45-52.

[55] HUSTON R L. Computer methods in flexible multibody dynamics[J]. International Journal for Numerical Methods in Engineering, 1991, 32: 1657-1668.

[56] GLADWELL G M L. Branch mode analysis of vibrating systems[J]. Journal of Sound and Vibration, 1964, 1(1): 41-59.

[57] YOO W S, HNAG E J. Dynamics of flexible mechanical systems using vibration and static corrected modes[J]. ASME J Mech, Transm, Autom, 1986, 108(3): 315-322.

[58] SHABANA A A. An absolute nodal coordinates formulation for the large rotation and deformation analysis of flexible bodies[R]. University of Illinois at Chicago, MBS96-1-UIC, 1996.

[59] 劉錦陽, 李彬, 洪嘉振. 作大范圍運動的柔性梁的剛-柔耦合動力學[J]. 力學學報, 2006, 38(2): 276-282.

[60] 劉鉞, 田強, 胡海巖. 基于絕對節點坐標的多柔體系統動力學高效計算方法[J]. 力學學報, 2010, 42(6): 1197-1205.

[61] 章仁為. 衛星軌道姿態動力學與控制[M]. 北京: 北京航空航天大學出版社, 1998: 298-316.

[62] 韓廣才, 張耀良. 雙自旋人造衛星的姿態動力學方程和穩定性研究[J]. 哈爾濱工程大學學報, 2004, 15(1): 94-99.

[63] REDMOND J, SILVERBERG L. Fuel optimal reorientation of axisymmetric spin-stabilized satellites[J]. Journal of Guidance, Control, and Dynamics, 1992, 16(1): 217-219.

[64] FRAITURE L. Slew calibration for spin-stabilized satellites[J]. Journal of Spacecraft and Rockets, 2000, 37(6): 784-787.

[65] CHERCHAS D B, HUGHES P C. Attitude stability of a dual-spin satellite with a large flexible solar array[J]. Journal of Spacecraft and Rockets, 1973, 10(2): 126-132.

[66] WERTZ J R. Spacecraft attitude determination and control[M]. Dordrecht: Kluwer Academic Publishers, 1978.

[67] WIE B. Space vehicle dynamics and control[M]. Reston: AIAA Education Series， 1998.

[68] 張銀輝, 楊華波, 江振宇, 等. 基于干擾估計的航天器大角度姿態機動魯棒次優控制[J]. 宇航學報, 2015, 36(10): 1148-1154.

[69] 劉付成, 朱東方, 宋婷, 等. 帶大慣量運動部件衛星姿態高精度復合控制研究[J]. 上海航天, 2016, 33(6): 53-60.

[70] CACCAVALE F, VILLANI L. Output feedback control for attitude tracking[J]. Systems and Control Letters, 1999, 38(2): 91-98.

[71] EI-KHAZALI R, DECARLO R A. Output feedback variable structure controllers design[J]. Automatica, 1995, 31(6): 805-816.

[72] ZHENG Y. Output feedback variable structure adaptive control of a flexible spacecraft[J]. Acta Astronautica, 1999, 44(1): 11-22.

[73] SHEN Y, LIU C, HU H. Output feedback variable structure control for uncertain systems with input nonlinearities[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(4): 762-764.

[74] 胡慶雷, 李理. 考慮輸入飽和與姿態角速度受限的航天器姿態抗退繞控制[J]. 航空學報, 2015, 36(4): 1259-1266.

[75] TSIOTRAS P. Further passivity results for the attitude control problem[J]. IEEE Transactions on Automatic Control, 1998, 43(11): 1597-1600.

[76] CROUCH P E. Spacecraft attitude control and stabilization: applications of geometric control theory to rigid body models[J]. IEEE Transactions on Automatic Control, 1984, 29(4): 321-331.

[77] BROCKETT R W. Asymptotic stability and feedback stabilization[J]. Differential Geometric Control Theory, 1985, 6(1): 181-191.

[78] OUTBIB R, SALLET G. Stabilizability of the angular velocity of a rigid body revisited[J]. Systems and Control Letters, 1992, 18(2): 93-98.

[79] KRISHNAN H, REYHANOGLU M, MCCLAMROCH H. Attitude stabilization of a rigid spacecraft using two control torques: a nonlinear control approach based on the spacecraft attitude dynamics[J]. Automatica, 1994, 30(6): 1023-1027.

[80] 黃興宏, 徐世杰. 欠驅動航天器的分段解耦姿態控制[J]. 宇航學報, 2007, 28(3): 531-535.

[81] CASAGRANDE D, ASTOLFI A, PARISINI T. Global asymptotic stabilization of the attitude and the angular rates of an underactuated non-symmetric rigid body[J]. Automatica, 2008, 44: 1781-1789.

[82] 宋道喆, 耿云海, 易濤. 零角動量欠驅動航天器逆最優穩定控制律設計[J]. 宇航學報, 2016, 37(6): 729-736.

[83] SAMSON C. Velocity and torque feedback control of a nonholonomic cart[C]// Proceedings of the International Workshop on Nonlinear and Adaptive Control: Issues in Robotics. Springer Verlag: [s. n.], 1991: 125-151.

[84] MORIN P, SAMSON C, POMET J B, et al. Time-varying feedback stabilization of the attitude of a rigid spacecraft with two controls[J]. Systems and Control Letters, 1995, 25: 375-385.

[85] MORIN P, SAMSON C. Time-varying exponential stabilization of a rigid spacecraft with two control torques[J]. IEEE Transactions on Automatic Control, 1997, 42(4): 528-534.

[86] 張佳為, 許諾, 伍少雄. 欠驅動航天器飛輪控制方法[J]. 宇航學報, 2016, 37(5): 552-561.

[87] 王冬霞, 賈英宏, 金磊, 等. 欠驅動航天器姿態穩定的分層滑模控制器設計[J]. 宇航學報, 2013, 34(1): 17-24.

[88] 馬廣富, 劉剛, 黃靜, 等. 欠驅動航天器姿態調節滑模控制[J]. 哈爾濱工業大學學報, 2012, 44(9): 1-6.

[89] 屠善澄. 衛星姿態動力學與控制(二)[M]. 北京: 中國宇航出版社, 1998.

[90] ZHENG J S P, ALLEYNE B H. Optimal attitude control for three-axis stabilized flexible spacecraft[J]. Acta Astronautica, 2005, 56: 219-528.

[91] 蔡鵬, 王慶超. 基于自適應模糊觀測器的撓性航天器主動振動抑制方法研究[J]. 宇航學報, 2009, 30(3): 890-894.

[92] 孫小松, 耿云海, 楊滌. 中繼衛星H∞姿態穩定控制研究[J]. 航空學報, 2006, 27(3): 465-473.

[93] 李順利, 李立濤, 楊旭. 柔性多體衛星自抗擾控制系統的研究[J]. 宇航學報, 2007, 28(4): 845-849.

[94] 李洋, 仇原鷹, 張軍, 等. 一種撓性航天器的自適應姿態控制與振動控制[J]. 振動與沖擊, 2009, 28(12): 178-182.

[95] 白圣建, 黃新生. 基于TS模糊區域模型的航天器姿態控制[J]. 控制工程, 2011, 18(6): 947-951.

[96] 王松, 崔平遠, 張池平, 等. 柔性航天器姿態的在線神經網絡控制[J]. 飛行力學, 1998, 16(2): 83-89.

[97] FERRI A A. Friction damping and isolation system[J]. Journal of Dynamics Systems, Measurement and Control, 1995, 117(2): 196-206.

[98] ANANDAKRISHNAN S M, CONNOR C T, LEE S, et al. Hubble space telescope solar array damper for improving control system stability[C]// IEEE Aerospace Conference Proceedings. [S. l.]: [s. n.], 2000: 261-276.

[99] 趙超, 周軍, 周鳳岐. 大型復合航天器的建模與分散控制技術[J]. 飛行力學, 1998, 16(3): 22-27.

[100] 林西強, 李東旭. 大型柔性空間結構的多級分散化振動控制[J]. 國防科技大學學報, 1996, 18(1): 23-28.

[101] 黃圳圭. 航天器姿態動力學[M]. 長沙: 國防科技大學出版社, 1997.

[102] ZHANG X M, EEDMAN A G. Optimal placement of piezoelectric sensors and actuators for controlled flexible linkage mechanisms[J]. Journal of Vibration and Acoustics, Transactions of the ASME, 2006, 128(2): 256-260.

[103] BRUANT I, PROSLIER L. Optimal location of actuators and sensors in active vibration control[J]. Journal of Intelligent Material System and Structures, 2005, 16: 197-206.

[104] SUNAR M, RAO S S. Thermo piezoelectric control design and actuator placement[J]. AIAA Journal, 1997, 35(2): 534-539.

[105] 周星德, 汪鳳泉. 基于可靠性的框架結構作動器/傳感器最優配置[J]. 東南大學學報(自然科學版), 2003, 33(6): 746-749.

[106] RYOU J K, PARK K Y, KIM S J. Electrode pattern design of piezoelectric sensors and actuators using genetic algorithms[J]. AIAA Journal, 1998, 36(2): 227-233.

[107] DHURI K D, SESHU P. Favorable locations for piezo actuators in plates with good control effectiveness and minimal change in system dynamics[J]. Smart Material and Structures, 2007, 16: 2526-2542.

[108] ALI R M, AGHIL Y K. Optimal positioning of piezoelectric actuators on a smart fin using bio-inspired algorithms[J]. Aerospace Science and Technology, 2007, 11: 174-182.

[109] HAO H N. Optimal number and placements of piezoelectric patch actuators in structural active vibration control[J]. Engineering Computations, 2004, 21(6): 651-665.

[110] TZOU H. Piezoelectric shells-distributed sensing and control of continua[M]. New York: Springer Science & Business Media, 2012.

[111] WANG D A, HUANG Y M. Modal space vibration control of a beam by using the feedforward and feedback control loops[J]. International Journal of Mechanical Sciences, 2002, 44(1): 1-19.

[112] 林建華. 結構模態控制的“溢出”問題及控制策略[J]. 華僑大學學報(自然科學版), 1999, 20(4): 366-371.

[113] SHAN J J, LIU H T, SUN D. Slewing and vibration control of a single-link flexible manipulator by positive position feedback[J]. Mechatronics, 2005, 15(4): 487-503.

[114] 仝西岳, 李東旭. 線性大系統的分散協同H∞狀態反饋控制[J]. 東南大學學報(自然科學版), 2005, 35(S2): 48-52.

[115] LAPPAS V J, STEYN W H, UNDERWOOD C I. Attitude control for small satellite using control moment gyros[J]. Acta Astronautica, 2002, 51(1): 101-111.

[116] LAPPAS V J, OOSTHUIZEN P, MADLE P, et al. Design, analysis and in-orbit performance of the BILSAT-1 microsatellite twin CMG experimental cluster[C]// AIAA Guidance, Navigation, and Control Conference and Exhibit. Rhode Island: AIAA, 2004: 5246.

[117] WIE B, HEIBERG C, BAILEY D. Rapid multi-target acquisition and pointing control of agile spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2002, 25(1): 96-104.

[118] CAO X, YUE C, LIU M, et al. Time efficient spacecraft maneuver using constrained torque distribution[J]. Acta Astronautica, 2016, 123: 320-329.

[119] DWYER T A W, SIRA-RAMIREZ H. Variable-structure control of spacecraft attitude maneuvers[J]. Journal of Guidance, Control, and Dynamics, 1998, 11(3): 262-270.

[120] GAO J, CAI Y. Adaptive finite-time control for attitude tracking of rigid spacecraft[J]. Journal of Aerospace Engineering, 2016, 29(4): 04016016.

[121] ALI I, RADICE G, KIM J. Backstepping control design with actuator torque bound for spacecraft attitude maneuver[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(1): 254-259.

[122] HOWLEY B. Genetic programming of near-minimum-time spacecraft attitude maneuvers[C]// Proceedings of the 1stAnnual Conference on Genetic Programming. Cambridge: MIT Press, 1996: 98-106.

[123] CHEN X J, STEYN W H. Robust combined eigenaxis slew manoeuvre[C]// AIAA Guidance, Navigation and Control Conference. Portland: AIAA, 1999: 4048.

[124] HAO T, MATUNAGA S. New sliding mode control approach for rapid attitude maneuver using control moment gyros[J]. Journal of Aerospace Engineering, 2015, 29(2): 06015001.

[125] JIKUYA I, FUJII K, YAMADA K. Attitude maneuver of spacecraft with a variable-speed double-gimbal control moment gyro[J]. Advances in Space Research, 2016, 58: 1303-1317.

[126] BILIMORIA K D, WIE B. Time-optimal three-axis reorientation of a rigid spacecraft[J]. Journal of Guidance, Control, and Dynamics, 1993, 16(3): 446-452.

[127] BAI X L, JUNKINS J L. New results for time-optimal three-axis reorientation of a rigid spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(4): 1071-1076.

[128] 劉剛. 應用控制力矩陀螺的衛星姿態機動控制研究[D]. 哈爾濱: 哈爾濱工業大學, 2010.

[129] SHEN H J, TSIOTRAS P. Numerical approach for solving rigid spacecraft minimum time attitude maneuvers[J]. Journal of Guidance, Control, and Dynamics, 1990, 13(1): 38-45.

[130] ZHANG S, FRISWELL M I, WAGG D J, et al. Rapid path planning for zero-propellant maneuvers[J]. Journal of Aerospace Engineering, 2015, 29(3): 04015078.

[131] FLEMING A, SEKHAVAT P, ROSS I M. Minimum-time reorientation of a rigid body[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(1): 160-170.

[132] KARPENKO M, BHATT S, BEDROSSIAN N, et al. First flight results on time-optimal spacecraft slews[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(2): 367-376.

[133] MCLNNES C R, Large angle slew maneuvers with autonomous sun vector avoidance[J]. Journal of Guidance, Control, and Dynamics, 1994, 17(4): 875-877.

[134] WISNIEWSKIA R, KULCZYCKI P. Slew maneuver control for spacecraft equipped with star camera and reaction wheels[J]. Control Engineering Practice, 2005, 13: 349-356.

[135] RADICE G, CASASCO M, Time-varying potential function control for constrained attitude tracking[J]. Advances in Astronautical Sciences, 2005, 119(1): 555-574.

[136] AVANZINI1 G, RADICE G, ALI I. Potential approach for constrained autonomous manoeuvres of a spacecraft equipped with a cluster of control moment gyroscopes[J]. Journal of Aerospace Engineering, 2009, 223(3): 285-296.

[137] HABLANI H B. Attitude commands avoiding bright objects and maintaining communication with ground station[J]. Journal of Guidance, Control, and Dynamics, 1999, 22(6): 759-767.

[138] SINGH G, MACALA G, WONG E, et al. A constraint monitor algorithm for the Cassini spacecraft[C]// Proceedings of the AIAA Guidance, Navigation, and Control Conference. Reston: AIAA, 1997: 3526.

[139] FRAZZOLI E, DAHLEH M A, FERON E. A randomized attitude slew planning algorithm for autonomous spacecraft[R]. AIAA, 2001-4155, 2001.

[140] KIM Y, MESBAHI M. Quadratically constrained attitude control via semidefinite programming[J]. IEEE Transactions on Automatic Control, 2004, 49(5): 731-735.

[141] SPILLER D, ANSALONE L, CURTI F. Particle swarm optimization for time-optimal spacecraft reorientation with keep-out cones[J]. Journal of Guidance, Control, and Dynamics, 2015, 39(2): 312-325.

[142] 程小軍, 崔祜濤, 徐瑞, 等. 幾何約束下的航天器姿態機動控制[J]. 控制與決策, 2012, 27(5): 724-730.

[143] XU R, WU C, ZHU S, et al. A rapid maneuver path planning method with complex sensor pointing constraints in the attitude space[J]. Information Systems Frontiers, 2016, doc: 1007/s10796-016-9642-1.

[144] ZHAO Q, HUANG H. Multi-objective optimization of zero propellant maneuver using hybrid programming[J]. Acta Astronautica, 2015, 116: 154-160.

[145] BALLOIS S L, DUC G.H∞control of an earth observation satellite[J]. Journal of Guidance, Control, and Dynamics. 1996, 19(3): 628-635.

[146] MIRSHAMS M, KHOSROJERDI M, HASSANI M. Passive fault tolerant sliding mode attitude control for flexible spacecraft with faulty thrusters[J]. Proceedings of the Institution of Mechanical Engineers Part G: Journal of Aerospace Engineering, 2013, 228(12): 2343-2357.

[147] 于亞男, 胡存明, 賀從園, 等. 基于高階滑模變結構的撓性航天器大角度姿態機動控制研究[J]. 上海航天, 2016, 33(3): 55-60.

[148] 劉敏, 徐世杰, 韓潮. 撓性航天器姿態機動直接自適應主動振動控制[J]. 北京航空航天大學學報, 2013, 39(3): 285-289.

[149] ZHONG C X, GUO Y, YU Z. A self-adjusting sliding-mode control based on RBF neural network for flexible spacecraft attitude[C]// IEEE International Conference on Information and Automation. Yinchuan: IEEE, 2013: 207-212.

[150] 陜晉軍, 劉暾. 應用分力合成主動振動抑制方法的最優飛行器大角度機動控制策略[J]. 航空學報, 2002, 23(1): 62-65.

[151] PAI M C. Robust input shaping control for multi-mode flexible structures using neuro-sliding mode output feedback control[J]. Journal of the Franklin Institute, 2012, 349(3): 1283-1303.

[152] 胡恒建， 李英波， 施桂國，等. 空間站帆板驅動輸入成型魯棒控制[J]. 上海航天， 2016, 33(1): 13-17.

[153] SINGER N C, SEERING W P. Preshaping command inputs to reduce system vibration[J]. Journal of Dynamic Systems, Measurement, and Control, 1990, 112(1): 76-82.

[154] SINGHOSE W E, DEREZINSKI S, SINGER N. Extra-insensitive input shapers for controlling flexible spacecraft[J]. Journal of Guidance, Control, and Dynamics, 1996, 19(2): 385-391.

[155] SINGHOSE W E. Command generation for flexible systems[D]. Cambridge: Massachusetts Institute of Technology, 1997: 285.

[156] 孔憲仁, 楊正賢, 葉東, 等. 基于輸入成形的柔性航天器振動閉環抑制方法研究[J]. 振動與沖擊, 2010, 29(3): 72-76.

[157] 施桂國, 朱慶華, 張子龍. 一種主動抑制太陽帆板撓性振動的控制策略研究[J]. 上海航天, 2016, 33(3): 61-70.

[158] 胡慶雷, 馬廣富. 基于滑模輸出反饋與輸入成形控制相結合的撓性航天器主動振動抑制方法[J]. 振動與沖擊, 2007, 26(6): 133-138.

[159] ZHAO L, WU X, HAO Y, et al. A novel method of vibration suppression for multi-modal flexible spacecraft[C]// 33th Chinese Control Conference. Nanjing: [s. n.], 2014: 8822-8825.

[160] 苗雙全, 叢炳龍, 劉向東. 基于輸入成形的撓性航天器自適應滑模控制[J]. 航空學報, 2013, 34(8): 1906-1914.

[161] ZHONG C, GUO Y, YU Z, et al. Finite-time attitude control for flexible spacecraft with unknown bounded disturbance[J]. Transactions of the Institute of Measurement and Control, 2016, 38(2): 240-249.

[162] VECIANA1 J M, CARDONA1 S, CATALP. Minimizing residual vibrations for non-zero initial states: application to an emergency stop of a crane[J]. International Journal of Precision Engineering and Manufacturing, 2013, 14(11): 1901-1908.

[163] 雷擁軍, 談樹萍, 劉一武. 一種航天器姿態快速機動及穩定控制方法[J]. 中國空間科學技術, 2010, 30(5): 48-53+58.

[164] SINGHOSE W, BIEDIGER E, OKADA H. Control of flexible satellites using analytic on-off thruster commands[R]. AIAA, 2003-5333, 2003.

[165] JUNKINS J L, RAHMAN Z, BANG H. Near minimum-time maneuvers of flexible vehicles: a liapunov control law design method[J]. Mechanics and Control of Large Flexible Structures, Progress in Astronautics and Aeronautics, 1990, 129: 565-593.

[166] 劉德慶， 彭仁軍， 張子龍. 基于路徑規劃和輸入成型的撓性航天器振動控制方法[J]. 上海航天，2014, 31(4): 41-72.

[167] KIM J J, AGRAWAL B N. Experiments on Jerk-limited slew maneuvers of a flexible spacecraft[R]. AIAA, 2006-6187, 2006.

[168] FARRENKOPF R L. Optimal open-loop maneuver profiles for flexible spacecraft[J]. Journal of Guidance and Control, 1979, 2(6): 491-498.

[169] 于亞男, 李克勇, 陳海朋, 等. 撓性航天器大角度快速機動復合控制[J]. 航天控制, 2016, 34(4): 36-41.

[170] BIAGIOTTI L, MELCHIORRI C. FIR filters for online trajectory planning with time-and frequency-domain specifications[J]. Control Engineering Practice, 2012, 20: 1385-1399.

[171] 楊樂平, 朱彥偉, 黃煥. 航天器相對運動軌跡規劃與控制[M]. 長沙: 國防工業出版社, 2010: 26-28.

[172] 李俊峰, 高云峰, 寶音賀西， 等. 衛星編隊飛行動力學與控制研究[J]. 力學與實踐, 2002, 24(2): 1-6.

[173] ALFRIEND K T, SCHAUB H, GIM D W. Gravitational perturbations nonlinearity and circular orbit on formation flying control strategies[J]. Guidance and Control, 2000: 139-158.

[174] 龔勝平, 李俊峰, 寶音賀西. 小天體伴飛脈沖控制[J]. 中國空間科學技術, 2013, 33(3): 15-21.

[175] CARTER T E. Linearized impulsive rendezvous problem[J]. Journal of Optimization Theory and Applications, 1995, 86(3): 553-584.

[176] VADDI S S, VADALI S R, ALFRIEND K T. Formation flying: accommodating nonlinearity and eccentricity perturbations[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(2): 214-223.

[177] KARLGAARD C D, LUTZE F H. Second-order equations for rendezvous in a circular orbit[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(3): 499-501.

[178] 高云峰, 寶音賀西, 李俊峰. 衛星編隊飛行的動力學特性與相對軌道構形仿真[J]. 清華大學學報(自然科學版), 2002, 42(4): 458-461.

[179] SENGUPTA P, VADALI S R. ALFRIEND K T. Modeling and control of satellite formations in high eccentricity orbits[J]. Journal of the Astronautical Sciences, 2004, 52(1-2): 149-168.

[180] SCHAUB H, ALFRIEND K T. Hybrid cartesian and orbit element feedback law for formation flying spacecraft[J]. Journal of Guidance, Navigation, and Control, 2002, 25(2): 387-393.

[181] 肖業倫, 張曉敏. 編隊飛行衛星群的軌道動力學特性與構型設計[J]. 宇航學報, 2001, 22(4): 7-12.

[182] GURFIL P. Generalized solutions for relative spacecraft orbits under arbitrary perturbations[J]. Acta Astronautica, 2007, 60: 61-78.

[183] 曹靜, 袁建平, 羅建軍. 橢圓軌道非線性相對運動模型的周期解與應用[J]. 中國空間科學技術, 2013, 33(3): 37-45.

[184] 彭冬亮, 荊武興, 徐世杰. 停靠階段軌道姿態耦合動力學與控制研究[J]. 飛行力學, 2002, 20(1): 33-37.

[185] 鐵鈺嘉, 楊偉, 岳曉奎. 航天器姿軌耦合非線性同步控制[J]. 計算機仿真, 2012, 29(3): 126-131.

[186] 楊佳, 朱戰霞, 張艷召. 繞飛監測小衛星姿軌聯合自適應控制研究[J]. 飛行力學, 2008, 26(5): 59-62.

[187] 吉莉. 內編隊重力場測量衛星系統控制方法研究[D]. 長沙: 國防科學技術大學, 2012.

[188] 廖飛, 季海波, 解永春. 追蹤器本體坐標系下航天器姿軌一體化控制律設計[J]. 控制與決策, 2015, 30(9): 1679-1684.

[189] JUNKINS J L, TURNER J D. On the analogy between orbital dynamics and rigid body dynamics[J]. Journal of the Astronautical Sciences, 1979, 27(4): 345-358.

[190] PLOEN S R, HADAEGH F Y, SCHARF D P. Rigid body equations of motion for modeling and control of spacecraft formations-part 1: absolute equations of motion[C]// Proceeding of the 2004 American Control Conference. Boston: [s. n.], 2004: 3646-3653.

[191] ZHANG F, DUAN G R. Robust integrated translation and rotation finite-time maneuver of a rigid spacecraft based on dual quaternion[C]// AIAA Guidance, Navigation, and Control Conference. Portland: AIAA, 2011: 6396.

[192] 王劍穎, 梁海朝, 孫兆偉. 基于對偶四元數的相對耦合動力學與控制[J]. 宇航學報, 2010, 31(7): 1711-1717.

[193] 朱戰霞, 馬家瑨, 樊瑞山. 航天器相對運動姿軌耦合特性研究[J]. 西北工業大學學報, 2015, 33(6): 887-891.

[194] KAPILA V, SPARKS A G, JAMES M B. Spacecraft formation flying: dynamics and control[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(3): 561-564.

[195] QI G Y. Nonlinear dynamics and output feedback control of multiple spacecraft in elliptical orbits[C]// American Control Conference, Proceedings of the 2000. Chicago: IEEE, 2000, 2: 839-843.

[196] KUMAR B S, EYER J K. Averaged relative states for spacecraft formation control in the presence ofJ2disturbances[J]. Acta Astronautica, 2012, 77: 61-67.

[197] 王兆魁, 張育林. 分布式衛星精確構形保持變結構控制[J]. 航天控制, 2005, 23(6): 27-30.

[198] 岳曉奎, 段遜. 基于偽譜同倫算法的編隊衛星任務設計研究[J]. 上海航天, 2016, 33(6): 44-50.

[199] 劉少然, 曾國強. 編隊飛行航天器平均軌道根數非線性控制研究[J]. 中國空間科學技術, 2005, 25(5): 24-61.

[200] 曹喜濱, 賀東雷. 攝動橢圓參考軌道編隊相對運動方程[J]. 吉林大學學報(工學版), 2009, 39(1): 234-239.

[201] HAMEL J F, LAFONTAINE J. Neighboring optimum feedback control law for earth-orbiting formation-flying spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(1): 290-299.

[202] NO T S, LEE J G, Jr COCHRAN J E. Spacecraft formation-keeping using a closed-form orbit propagator and optimization technique[J]. Acta Astronautica, 2009, 65: 537-548.

[203] BAE J, KIM Y, PARK C. Spacecraft formation flying control using sliding mode and neural networks controller[C]// AIAA Guidance, Navigation, and Control Conference. Chicago: AIAA, 2009: 5671.

[204] SUN H B, LI S H, FEI S M. A composite control scheme for 6 DOF spacecraft formation control[J]. Acta Astronautica, 2011, 69: 595-611.

[205] WU Y H, CAO X B, XING Y J, et al. Relative motion decoupled control for spacecraft formation with coupled translational and rotational dynamics[C]// International Conference on Computer Modeling and Simulation. [S. l.]: [s. n.], 2009: 63-68.

[206] WONG H, PAN H Z, KAPILA V. Output feedback control for spacecraft formation flying with coupled translation and attitude dynamics[C]// Proceedings of the American Control Conference. Portland: [s. n.], 2005: 2419-2426.

[207] CHUANG S J, AHSUN U E, SLOTINE J J. Application of synchronization to formation flying spacecraft: Lagrangian approach[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(2): 512-526.

[208] PAN H, KAPILA V. Adaptive nonlinear control for spacecraft formation flying with coupled translational and attitude dynamics[C]// Proceedings of 40th IEEE Conference on Decision and Control. New York: Inst of Electrical and Electronics Engineers, 2001: 2057-2062.

[209] STANSBERY D T, CLOUTIER J R. Position and attitude control of a spacecraft using the state-dependent riccati equation technique[C]// Proceedings of the American Control Conference. Chicago: IEEE, 2000: 1867-1871.

[210] 李鵬, 岳曉奎, 袁建平. 基于θ-D方法的在軌操作相對姿軌耦合控制[J]. 中國空間科學技術, 2012, 32(4): 8-14.

[211] 李鵬, 岳曉奎, 袁建平. 對翻滾非合作目標終端逼近的姿軌耦合退步控制[J]. 哈爾濱工業大學學報, 2013, 45(1): 94-100.

[212] 李九人, 李海陽, 唐國金. 對無控旋轉目標逼近的自適應滑模控制[J]. 宇航學報, 2011, 32(4): 816-822.

[213] 宋斌, 馬廣富, 李傳江. 基于自適應滑模方法的航天器位置與姿態控制[J]. 哈爾濱工業大學學報, 2008, 40(9): 1353-1357.

[214] SHUICHI M, STEPHEN J, STEVEN D, et al. Approach planning and guidance for uncontrolled rotating satellite capture considering collision avoidance[C]// The 7th International Symposium on Artificial Intelligence, Robotics and Automation in Space. [S. l.]: [s. n.], 2003: i-SAIRAS.

[215] SUBBARAO K, WELSH S. Nonlinear control of motion synchronization for satellite proximity operations[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(5): 1284-1294.

[216] MA Z, MA O, SHASHIKANTH B N. Optimal approach to and alignment with a rotating rigid body for capture[J]. Journal of the Astronautical Sciences, 2007, 55(4): 407-419.

[217] GEORGE B, OLEG Y, MARCELLO R. Formulation and analysis of matching points of interest in two-spacecraft for optimal rendezvous[R]. AIAA, 2009-5669, 2009.

[218] SEBOLDT W, LEIPOLD M, REZAZAD M, et al. Ground-based demonstration of solar sail technology[C]// 51st International Astronautical Congress. Rio de Janeiro: [s. n.], 2000: IAF-00-S.6.

[219] MCINNES C R, MACDONALD M, HUGHES G. Mars sample return: technical assistance in the study of science payloads transported through solar sailing, technical note 1[R]. ESA: ES-TEC 16534/02/NL/NR, 2003.

[220] JOHNSON L, WHORTON M, HEATON A, et al. A solar sail demonstration mission[J]. Acta Astronautica, 2011, 68(5): 571-575.

[221] BIDDY C, SVITEK T. Lightsail-1 solar sail design and qualification[C]// Proceedings of the 41st Aerospace Mechanisms Symposium. Pasadena: Jet Propulsion Laboratory, National Aeronautics and Space Administration, 2012: 451-463.

[222] TSUDA Y, MORI O. FUNASE R, et al. Achievement of IKAROS-Japanese deep space solar sail demonstration mission[J]. Acta Astronautica, 2013, 82(2): 183-188.

[223] 張洋. 太陽帆航天器姿態控制與軌跡優化研究[D]. 合肥: 中國科學技術大學, 2010.

[224] PRUSSING J E. Solar sailing: technology, dynamics, and mission applications[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(4): 768-778.[225] WIE B. Solar sail attitude control and dynamics, part II[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(4): 536-544.

[226] RIOS-REYES L, SCHEERES D J. Generalized models for solar sails[J]. Journal of Spacecraft and Rockets, 2005, 42(1): 182-185.

[227] MCINNES C R, BROWN J C. The dynamics of solar sails with a non-point source of radiation pressure[J]. Celestial Mechanics and Dynamical Astronomy, 1990, 49(3): 249-264.

[228] BAOYIN H, MCINNES C R. Solar sail Halo orbits at the sun-earth artificial L1 point[J]. Celestial Mechanics and Dynamical Astronomy, 2006, 94(2): 155-171.

[229] BOOKLESS J, MCINNES C. Control of Lagrange point orbits using solar sail propulsion[J]. Acta Astronautica, 2008, 62(2): 159-176.

[230] 龔勝平. 太陽帆航天器動力學與控制研究[D]. 北京: 清華大學, 2009.

[231] BIGGS J, MCINNES C, WATERS T. Stabilizing periodic orbits above the elliptic plane in the solar sail 3-body problem: Proceedings of 59th International Astronautical Congress[C]// Glasgow: 2008.

[232] 張輝. 太陽帆航天器軌道動力學與控制研究[D]. 合肥: 中國科學技術大學, 2014.

[233] FARRES A, JORBA A. Station keeping of a solar sail around a Halo orbit[J]. Acta Astronautica, 2014, 94(11): 527-539.

[234] 史曉寧, 榮思遠, 白瑜亮. 太陽帆航天器行星分段捕獲控制方法研究[J]. 上海航天, 2016, 33(2): 87-93.

[235] SHAHID K, KUMAR K D. Formation control at the sun-earth L2 libration point using solar radiation pressure[J]. Journal of Spacecraft and Rockets, 2010, 47(4): 614-626.

[236] SHAHID K, KUMAR K D. Multiple spacecraft formation reconfiguration using solar radiation pressure[J]. Acta Astronautica, 2014, 103(11): 269-281.

[237] KUMAR K D. Review of dynamics and control of nonelectrodynamic tethered satellite systems[J]. Journal of Spacecraft and Rockets, 2006, 43(4): 705-720.

[238] KRUIJFF M, VAN DER HEIDE E J, OCKELS W J. Data analysis of a tethered spaceMail experiment[J]. Journal of Spacecraft and Rockets, 2009, 46(6): 1272-1287.

[239] KRUPA M, POTH W, SCHAGERL M, et al. Modelling, dynamics and control of tethered satellite systems[J]. Nonlinear Dynamics, 2006, 43(1-2): 73-96.

[241] WILLIAMS P, WATANABE T, BLANKSBY C, et al. Libration control of flexible tethers using electromagnetic forces and movable attachment[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(5): 882-897.

[242] MANKALA K K, AGRAWAL S K. Equilibrium-to-equilibrium maneuvers of rigid electrodynamic tethers[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(3): 541-545.

[243] LANOIX E L M, MISRA A K, MODI V J, et al. Effect of electrodynamic forces on the orbital dynamics of tethered satellites[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(6): 1309-1315.

[244] CHERNOUS'KO F L. Dynamics of retrieval of a space tethered system[J]. Journal of Applied Mathematics and Mechanics, 1995, 59(2): 165-173.

[245] PELAEZ J. On the dynamics of the deployment of a tether from an orbiter: partⅡ exponential deployment[J]. Acta Astronautica, 1995, 36(6): 313-335.

[246] KUMAR K, PRADEEP S. Strategies for three dimensional deployment of tethered satellites[J]. Mechanics Research Communications, 1998, 25(5): 543-550.

[247] JIN D P, HU H Y. Optimal control of a tethered subsatellite of three degrees of freedom[J]. Nonlinear Dynamics, 2006, 46(1-2): 161-178.

[248] 劉瑩瑩, 周軍. 近距離繩系衛星動力學與釋放方法研究[J]. 系統仿真學報, 2008, 20(20): 5642-5645.

[249] 王曉宇, 文浩, 金棟平. 考慮姿態的繩系衛星后退時域回收控制[J]. 力學學報, 2010, 42(5): 919-925.

[250] 鐘睿, 徐世杰. 可變繩長繩系衛星系統的一種簡單張力控制策略[J]. 中國空間科學技術, 2009, 29(6): 66-73.

[251] 何勇, 梁斌, 徐文福, 等. 繩系衛星系繩參數的實時估計方法[J]. 哈爾濱工業大學學報, 2010, 42(7): 1033-1037.

[252] YU S H. Dynamic model and control of mass-distributed tether satellite system[J]. Journal of Spacecraft and Rockets, 2002, 39(2): 213-218.

[253] ZHOU X, LI J F, BAOYIN H X, et al. Equilibrium control of electrodynamic tethered satellite systems in inclined orbits[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(6): 1451-1454.

[254] MANKALA K K, AGRAWAL S K. Equilibrium-to-equilibrium maneuvers of flexible electrodynamic tethers in equatorial orbits[J]. Journal of Spacecraft and Rockets, 2006, 43(3): 651-658.

[255] 劉壯壯， 寶音賀西. 基于非線性單元模型的繩系衛星系統動力學[J]. 動力學與控制學報, 2012, 10(1): 21-26.

[256] 余本嵩, 文浩, 金棟平. 時變自由度繩系衛星系統動力學[J]. 力學學報, 2010, 42(5): 926-932.

[257] BARKOW B, STEINDL A, TROGER H. A targeting strategy for the deployment of a tethered satellite system[J]. IMA Journal of Applied Mathematics, 2005, 70(5): 626-644.

[258] TRAGESSER S G, TUNCAY A. Orbital design of earth-oriented tethered satellite formations[J]. Journal of the Astronautical Sciences, 2005, 53(1): 51-64.

[259] WILLIAMS T, MOORE K. Dynamics of tethered satellite formations[J]. Advances in the Astronautical Sciences, 2002, 112: 1219-1235.

[260] PIZARRO-CHONG A, MISRA A K. Dynamics of a multi-tethered satellite formation[C]// AIAA/AAS Astrodynamics Specialist Conference and Exhibit. [S. l.]: AIAA/AAS, 2004: 5308.

[261] KUMAR K D, YASAKA T. Rotating formation flying of three satellites using tethers[J]. Journal of Spacecraft and Rockets, 2004, 41(6): 973-985.

[263] GUERMAN A D, SMIRNOV G, PAGLIONE P, et al. Stationary configurations of a tetrahedral tethered satellite, formation[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(2): 424-428.

[264] BOMBARDELLI C, LORENZINI E C, QUADRELLI M B. Retargeting dynamics of a linear tethered interferometer[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(6): 1061-1067.

[265] KIM M, HALL C D. Control of a rotating variable-length tethered system[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(5): 849-858.

[266] KOJIMA H, IWASAKI M, FUJII H A, et al. Nonlinear control of librational motion of tethered satellites in elliptic orbits[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(2): 229-239.

[267] KOJIMA H, SUGIMOTO T. Nonlinear control of a double pendulum electrodynamic tether system[J]. Journal of Spacecraft and Rockets, 2007, 44(1): 280-284.

[268] WILLIAMS P. Optimal deployment/retrieval of a tethered formation spinning in the orbital plane[J]. Journal of Spacecraft and Rockets, 2006, 43(3): 638-650.

[269] MORI O, MATUNAGA S. Formation and attitude control for rotational tethered satellite clusters[J]. Journal of Spacecraft and Rockets, 2007, 44(1): 211-220.

[270] CHUNG S J, SLOTINE J J E, MILLER D W. Nonlinear model reduction and decentralized control of tethered formation flight[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(2): 390-400.

[271] CHANG I, PARK S Y, CHOI K. Nonlinear attitude control of a tether-connected multi-satellite in three-dimensional space[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(4): 1950-1968.

Review of Dynamics and Control Study of Spacecraft

LIU Fu-cheng1, 2, ZHU Dong-fang1, 2, HUANG Jing1, 2

(1. Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai 201109, China;2. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China)

In this paper, the recent development and research status of spacecraft dynamics and control were introduced. The basic issues in the study of single-satellite dynamics and control technology, multi-satellite dynamics and control technology, and advanced spacecraft (solar sail spacecraft and tethered satellite) dynamics and control technology were reviewed. The research methods and archivements in these areas were summarized. Finally, the lucubration and prospects for problem of dynamics and control of spacecraft were discussed, which were such as orbit dynamics of deep space exploration, dynamics modeling and joint control technology of ultra-size flexible spacecraft, maneuvering control technology of agile satellite, attitude and orbit coupling dynamics and control of multi-satellite, dynamics and control technology of solar sail spacecraft, and dynamics and control technology of tethered satellites system.

spacecraft; dynamics; orbit control; attitude control; rigid body; flexibility; attitude and orbit coupling; agile satellite; solar sail spacecraft; tethered satellite

1006-1630(2017)02-0001-29

2017-02-24；

2017-03-13

上海市自然科學基金資助(16ZR1415700)；上海市科技人才計劃資助(14XD1421400);上海市青年科技英才揚帆計劃資助(14YF1414500，15YF1405200，17YF1408400)

劉付成(1973—)，男，博士，研究員，主要從事航天器控制系統設計和研究。

V412.4；V448.2

A

10.19328/j.cnki.1006-1630.2017.02.001