基于GPS測量數據的衛星在軌軌道預報算法研究

劉 燎,孫華苗,李立濤,張迎春，

(1.深圳航天東方紅海特衛星有限公司,廣東 深圳 518064; 2.哈爾濱工業大學 航天學院,黑龍江 哈爾濱 150001)

?

基于GPS測量數據的衛星在軌軌道預報算法研究

劉 燎1,孫華苗1,李立濤2,張迎春1， 2

(1.深圳航天東方紅海特衛星有限公司,廣東 深圳 518064; 2.哈爾濱工業大學 航天學院,黑龍江 哈爾濱 150001)

為提高微小衛星的在軌軌道預報能力，針對常用的低軌近圓衛星軌道，根據解析的軌道動力學模型，基于無奇點變量的擬平均要素法，用Kalman濾波技術給出了一種衛星解析星歷參數在軌估計算法，用GPS測量信息對相關星歷模型參數進行在軌估計。給出了算法流程。先由外部標志判斷濾波器初始化狀態，若需初始化，則可基于GPS測量數據，或地面上注星歷參數，或上次濾波所得星歷參數進行；若初始化已完成，則對星歷模型參數進行Kalman濾波，得到更新的星歷參數。給出了濾波算法中軌道預報、殘差計算、量測計算和UD分解的計算模型。仿真結果表明：對軌道高度450 km以上的近地圓軌道，7 d內的預報精度優于20 km。算法具自啟動(自初始化)、收斂性佳、對測量數據的采樣要求不嚴格等優點，實用性好。

微小衛星； 自主能力； 低軌近圓衛星軌道； 星歷模型； 軌道預報； GPS測量數據； 擬平均要素； Kalman濾波

0 引言

隨著目前國內外衛星技術的不斷發展尤其是衛星組網的發展，對衛星在軌自主能力的需求不斷增加，在軌實時軌道確定成為判斷衛星是否具有自主能力的首要條件。隨著低成本全球導航系統接收機(包括美國的GPS及中國的北斗導航系統)的應用，在微小衛星上進行實時軌道確定進而提高小衛星的自主能力，已成為目前的一種發展趨勢[1-2]。

衛星星歷的計算有解析法、數值法和半解析法等三類，受星載計算機計算能力的制約，我國星上軌道預報目前都采用僅考慮地球非引力場主要帶諧項和大氣攝動主要長期項的擬平均要素法[3-4]。目前基于GPS測量信息的衛星實時在軌軌道確定主要采用Kalman濾波及基于軌道動力學模型的軌道確定技術，對衛星的瞬時軌道狀態(位置和速度矢量)或密切軌道要素進行估計，以實時提供衛星的高精度軌道確定信息。其結果主要用于衛星各種實時應用，如圖像的地理定位編碼、敏感器與可驅動天線的指向，以及衛星三軸姿態控制[5]。但采用這種軌道確定技術的導航系統，很難用于長期的在軌星歷預報(如數個軌道周期后甚至數天后的軌道預報)，而這恰是衛星自主任務規劃和自主管理所需的。其主要原因是：基于瞬時軌道參數或密切軌道要素進行軌道預報，需進行復雜的、計算量較大的軌道動力學數值積分運算，常需占用大量的星載計算機機時，因而不適于進行長期軌道預報[6]。文獻[7]提出了一種采用簡化的動力學模型和一種嵌套插值算法的積分器進行高精度的衛星星歷計算，可實現軌道預報1 d精度優于1 km的星歷計算，但也需要高性能的星載機，不適于微小衛星的軌道預報應用。

針對目前常用的低軌近圓衛星軌道，本文基于解析的軌道動力學模型，采用Kalman濾波技術，給出了一種衛星解析星歷參數在軌估計算法，利用GPS測量信息對相關星歷模型參數進行在軌估計[8]。可對任意時間間隔的衛星星歷進行預報，而不用按步長對軌道進行積分，其計算量相對較小，對星載機的性能要求不高，可滿足微小衛星的使用要求，能對衛星進行中期或長期的軌道預報(多個軌道周期或1周以上)。本文對基于GPS測量數據的衛星在軌軌道預報算法進行研究。算法具有自啟動(自初始化)、收斂性好、對測量數據的采樣要求不嚴格(允許測量數據以非均勻間隔時間給出，采樣時間可在數秒至十多分鐘內變化)的優點，甚至允許在軌道的某段時間內無測量數據情況下(如GPS天線被地球遮擋或接收機出現臨時性故障)，濾波器仍能正常運行。根據定義不同，平均要素又可分為平均要素和擬平均要素，其中平均要素只包含了長期變化項，擬平均要素包含長期變化項和長周期變化項，長周期變化項的周期能達到數月，因而在軌道問題研究中其影響不可忽略，同時擬平均要素能消除通約奇點問題，因而本算法采用基于無奇點變量的擬平均要素法[9]。為簡化星上計算量，計算過程僅考慮了一階精度。

1 星歷參數選擇

近地衛星主要受地球引力、大氣阻力、太陽光壓以及日月引力等作用，軌道變化包括長期變化項、長周期變化項和短周期變化項。長期變化即軌道參數隨時間的線性或二階及更高階的變化；長周期變化主要由地球引力場帶諧調和項引起；短周期項一類是由地球扁率引起的，另一類是由地球引力場的田諧調和項引起的。田諧項的攝動非常復雜，對小偏心率的軌道只需取其低頻部分便可獲得很高的精度，但在星上計算田諧項系數則需占據相當一部分內存和計算時間[10]。為簡化計算，在模型中僅考慮長期和長周期變化項。

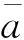
2 算法及計算流程

本文算法采用基于無奇點變量的擬平均要素法，使用Kalman濾波技術，利用GPS測量信息對相關星歷模型參數進行在軌估計。為減少濾波過程中計算誤差和舍入誤差對濾波器狀態誤差協方差矩陣正定性的影響，避免長時間計算過程濾波器發散，采用Bierman-UD分解形式的Kalman濾波技術。算法的流程如圖1所示。

本文算法的具體過程如下。

a)根據外部給出的是否進行濾波器初始化的標志判斷當前計算狀態。

b)若此時需進行初始化，則根據初始化方法標志分別進行濾波器初始化。此處：初始化方法有三種：一是根據GPS測量數據進行濾波器初始化，即由GPS提供的測量數據，計算所需測量時刻對應的軌道平要素集的初始猜測；二是根據地面上注的星歷模型參數進行初始化；三是用上次濾波器計算收斂獲得的星歷參數進行初始化。后兩種初始化方法基本相同。初始化完成后，將初始化標志置位。

c)若本次計算過程中初始化已完成，則進行Kalman濾波計算，對星歷模型參數進行濾波，得到更新的星歷參數。

3 基于GPS測量數據的初始化

利用GPS測量數據對歷元時刻軌道平要素濾波器進行初始化。即根據GPS提出的測量數據，計算所需測量時刻對應的軌道平要素集的初始猜值，該初始化過程如下。

a)將GPS測得的位置與速度矢量轉換至TOD系中；

b)將TOD坐標系中的位置與速度矢量轉換為瞬時軌道要素；

c)通過迭代計算平均軌道要素，并給出對應星歷模型參數；

d)根據提供的參數計算狀態誤差協方差矩陣，并進行UD分解；

e)輸出時刻tGPS對應的星歷模型參數以及初始U0，D0陣。

4 利用地面上注數據或上次濾波結果的初始化

本文算法是用地面上注的或前次Kalman濾波器給出的星歷模型參數，對本次濾波過程進行初始化，該初始化過程如下。

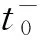
b)根據提供的參數計算狀態誤差協方差矩陣，并進行UD分解；

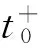
5 星歷模型參數濾波過程算法

本文算法是利用基于Bierman UD分解Kalman濾波公式對星歷模型參數進行濾波，得到更新的星歷參數以及協方差矩陣對應的U，D陣，濾波算法的主要計算步驟如下。

a)根據上一步濾波得到的星歷模型參數X以及其對應的歷元時刻t0，進行軌道預報，得當前GPS測量數據時刻tGPS對應的衛星位置矢量(TOD系中)。

b)計算殘差；若殘差大于給定的容限，則判斷為野值，退出當前濾波過程；否則執行步驟c)。

c)用有限差分法計算濾波所需的量測矩陣。

d)進行UD分解濾波，獲得更新星歷模型參數X+和協方差陣對應的U+，D+。

5.1 軌道預報算法

對時刻t0的星歷模型參數進行軌道外推，以獲得時刻t1的瞬時軌道位置和速度矢量(TOD系中)，計算過程如下。

a)根據歷元時刻t0及對應的星歷參數，計算獲得時刻t1的平均軌道參數

b)計算緯度幅角的平均值

c)計算時刻t1各軌道要素的短周期項

d)計算時刻t1的瞬時軌道要素

u=λ+2esinM+1.25e2sin(2M)

式中：X=a，i，Ω，ξ，η，λ。

e)計算時刻t1對應的位置與速度矢量

R=r(Pcosf+Qsinf)

5.2 殘差計算

根據時刻tGPS的GPS測量數據RGPS和進行軌道預報得到的時刻tGPS衛星位置矢量R計算殘差，計算步驟如下。

a)計算時刻tGPS的格林威治恒星時角S及坐標轉換矩陣Rz(S)

S=mod(S,2π)

b)計算殘差

5.3 量測矩陣計算

用有限差分方法計算衛星位置矢量預報值(TOD系)與星歷參數的偏導數矩陣，進而求得量測矩陣，計算步驟如下。

a)令i=1。

b)生成第i個元素帶擾動量的星歷參數向量

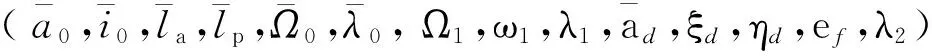
d)計算衛星位置矢量預報值與第i個星歷參數的偏導數矩陣

e)若i=14，則轉步驟f)，否則i=i+1，轉步驟b)。

f)計算量測噪聲矩陣H

5.4 UD分解濾波算法

本算法主要是對上一步濾波過程得到的協方差U陣和D陣以及濾波狀態進行更新，計算步驟如下。

a)令l=1，按以下步驟對第l個測量進行濾波更新。

b)計算變量αl和向量f，v，有

d)對濾波狀態量和協方差陣進行更新

e)若l大于等3,則計算結束；否則令l=l+1，轉步驟b)。

d)輸出Xk/k，Uk/k，Dk/k。

6 仿真驗證

為對本文提出的算法進行誤差分析，需有參考的精確衛星運行軌道。用衛星工具箱STK中的生成基準軌道，設仿真參數為：軌道積分HPOP；引力模型JGM-3；太陽光壓Cr=1.0，面質比0.02 m2/kg,陰影區模型Dual Cone；氣動阻力Cd=2.2，面質比0.02 m2/kg，大氣密度模型Jachia-Roberts；轉動慣量Ixx=4 500 kg·m2，Iyy=4 500 kg·m2，Izz=4 500 kg·m2；三體引力為太陽、地球、衛星。輸出的WGS84坐標系中衛星信息作為GPS測量數據，取采樣間隔分別為1，5 min，濾波時間5 d，對衛星的軌道進行預報，預報時間1～7 d，與生成的TOD系中軌道數據對比。所得軌道高度450，600，700，800 km的預報精度分別如圖2～9所示。

由圖2～9可知：對軌道高度500 km以上的近地近圓軌道，本文算法的擬合精度優于約1.5 km，在不同采樣間隔、不同軌道高度情況下，濾波2.5 d，預報1～7 d的軌道精度均優于20 km，可用于衛星光照/陰影區計算、地面站通信時機預報或地面成像目標規劃等任務，其時間精度優于3 s。

基于傳統14平軌道要素進行的軌道遞推仿真結果如圖10所示。由圖10可知：累積誤差較大，需定時由地面進行參數上注，不適于未來衛星自主任務管理發展的要求。

7 結束語

針對衛星長期自主運行需求，本文研究了基于GPS測量數據的衛星自主軌道預報方法。本文方法基于解析的軌道動力學模型，采用Kalman濾波技術，給出了一種衛星解析星歷參數在軌估計算法，軌道預報精度較前人方法有顯著提高；用基于Bierman UD分解的形式，可有效避免長時間計算引起的濾波器發散，自適應性好，對數據采樣要求不高，具較好的魯棒性，對微小衛星有較好的實用性，計算量少，降低了星載機的計算量，尤其適于低成本微小衛星的自主任務管理，可對衛星進行中期或長期的軌道預報(多個軌道周期或1周以上)。用數學仿真對本文方法的有效性進行了驗證。研究發現：本文算法采用基于無奇點變量的擬平均要素法，具有自啟動(自初始化)、收斂性好，且顯著減少了星上計算量，以及對測量數據的采樣要求不嚴(允許測量數據以非均勻間隔時間給出，采樣時間可在數秒至十多分鐘內變化)的優點；對軌道高度450 km以上的近地近圓軌道，在濾波2.5 d的條件下，預報精度優于20 km，軌道坐標系變換導致的誤差約0.012°，可用于中等精度的姿態確定。本文方法的缺點是僅適于近地圓軌道的軌道預報。此外，在建模中未考慮地球扁率和田諧攝動項的攝動影響。后續研究可在建模中加入各種攝動項的影響，提高預報精度并減少計算量。此外，對由GPS數據濾波初始化獲得的對應時刻的軌道平要素集的初始猜想值也可作進一步優化，以提高初始平要素的準確性。

[1] JOCHIM E F, GILL E, MONTENBRUCK O, KIRSCHNER M. GPS based onboard and on ground orbit operations for small satellites[J]. Acta Astronaut, 1996, 39(9-12): 917-922.

[2] MONTENBRUCK O, GILL E. Orbit determination of the MIR space station using MOMSNAV GPS measurements[C]// 20thInternational Symposium on Space Technology and Science, 11thInternational Symposium on Space Flight Dynamics. [S. l.]: [s. n.], 1996: 96-c-53.

[3] FONTE D. Comparison of orbit propagators in the research and development goddard trajectory determination system (R&D GTDS): partⅠ, simulated data[C]// AAS/AIAA Astrodynamics Specialist Conference. [S. l.]: AAS/AIAA, 1995: 432.

[4] 湯錫生. 載人飛船軌道確定和返回控制[M]. 北京: 國防工業出版社, 2002: 469-472.

[5] 鄧自立. 最優估計理論及其應用——建模、濾波、信息融合估計[M]. 哈爾濱: 哈爾濱工業大學出版社, 2005: 98-99.

[6] 張曉坤， 劉迎春， 楊新， 等. 近地衛星星歷的高精度星載算法研究[J]. 航天控制, 2005, 23(4): 41-44.

[7] GILL E. GPS-based autonomous navigation for the BIRD satellite: International Symposium on Spaceflight Dynamics[C]// [s. n.]: 2000.

[8] 劉林. 航天器軌道理論[M]. 北京: 國防工業出版社, 2000: 160-164.

[9] 楊維廉. 衛星軌道攝動頻譜分析[J]. 宇航學報, 1995, 16(4): 1-8.

[10] 楊維廉. 一種高精度的衛星星歷模型[J]. 航天器工程, 1996， 8(2): 21-32.

[11] 林波, 武云麗, 沈莎莎, 等. 軌道誤差對星敏感器對地指向精度的影響分析[J]. 空間控制技術與應用, 2013, 39(5): 24-28.

Research of a On-Board Orbit Prediction Method Based on GPS Data

LIU Liao1, SUN Hua-miao1, LI Li-tao2, ZHANG Ying-chun1, 2

(1. Shenzhen Aerospace Dongfanghong HIT Satellite Ltd, Shenzhen 518064, Guangdong, China;2. School of Astronautics, Harbin Institute of Technology, Harbin 150001, Heilongjiang, China)

To improve the capability of micro-satellite orbit prediction, an on-board model of ephemeris parameter was proposed by Kalman filter based on analytic orbit dynamic model and quasi-mean element method without singularity for near circular low earth orbit (LEO), which could estimate the relative ephemeris parameter using GPS data on-orbit. The algorithm flowchart was given. Firstly, the initial state of the filter was judged using external mark. If the initialization was needed, it could be implemented by GPS data, ephermeris parameters upload by the ground or ephermeris parameters obtained in the last filtering. If the initialization had been finished, the ephermeris parameters were treated to gain the new ephermeris parameters by Kalman filtering. The computation modes of orbit predication, residue error calculation, measurement calculation and Bierman-UD decomposing were presented. The simulation results showed that prediction accuracy was better than 20 km in the 7-days prediction for the near circular LEO which the altitude was higher than 450 km. The algorithm proposed had advantages such as self-start (self initialization), good convergence and not ridge requirement of measurement data sampling, which was practicable in engineering.

micro-satellite; self-management; near circular LEO; ephemeris parameter; orbit prediction; GPS data; quasi-mean element; Kalman filter

1006-1630(2017)02-0120-07

2016-08-17；

2016-11-28

國家自然科學基金資助(61473297)

劉 燎(1987—)，男，碩士，主要從事微小衛星姿態控制系統設計。

V448.2

A

10.19328/j.cnki.1006-1630.2017.02.013