一種應用于欠驅動航天器的姿態控制方法研究

劉美師,吳敬玉，王文妍，楊盛慶

(上海航天控制技術研究所,上海 201109)

?

一種應用于欠驅動航天器的姿態控制方法研究

劉美師,吳敬玉，王文妍，楊盛慶

(上海航天控制技術研究所,上海 201109)

對欠驅動航天器的姿態控制進行了研究，設計了一種可適于多種情況的分段解耦控制器，用分段解耦的方法解決了欠驅動控制系統輸入輸出維數不統一的問題。由動力學方程中的耦合項建立姿態控制系統的狀態微分方程。為降低失效軸角速度對系統的影響，先實現控制系統中動力學部分的鎮定，再對運動學部分進行解耦。在每個分段中設計了一個比例微分(PD)控制器，設計了角速度鎮定、俯仰角鎮定、滾動角鎮定、俯仰角收斂至π/2、偏航角鎮定和三軸穩定六個分段控制器，通過控制器間的逐個切換控制，將狀態微分方程中的狀態變量逐漸收斂至零，實現欠驅動姿態控制系統的漸進穩定。數學仿真驗證了所設計控制算法的有效性。該控制器設計簡單，便于工程實現，選取適當的參數后可保證系統狀態變量的漸近穩定性。

欠驅動航天器； 姿態控制； 分段解耦； 維數； 耦合； 微分方程； 切換控制； 漸進穩定

0 引言

欠驅動控制系統是指系統輸入維數低于其位形自由度的系統[1]。當航天器姿態控制系統的部分執行機構失效而導致其無法提供完整的三軸控制力矩時，便成為欠驅動航天器。欠驅動航天器的姿態控制系統中執行機構處于一種非完整配置狀態，是一種具不可積分約束的本質非線性系統[2]。因此，常規的線性控制方法，如光滑定常反饋控制等現代控制理論不能直接用于解決欠驅動系統的穩定控制問題。

1984年，對欠驅動航天器進行了最早的理論研究。文獻[3]基于微分幾何理論針對剛性航天器在有1、2、3個獨立控制輸入力矩的情況下，給出了航天器能控的充要條件，并證明欠驅動航天器若是非軸對稱的，則航天器在任意的平衡點都是局部能控的。文獻[4]以兩個飛輪為執行機構，并在整星零動量條件下用遺傳算法研究了欠驅動航天器的非完整運動規劃問題，用最優控制方法和Ritz近似理論獲得了以兩動量飛輪為執行機構的控制輸入規律，推導出軸對稱欠驅動航天器姿態軌跡可行的必要條件，然后由系統的微分平滑特性規劃出一組滿足上述條件的可行軌跡。為實現欠驅動航天器在兩個給定姿態間的轉移，通常的方式有兩種：基于最優控制策略的軌跡規劃算法或基于航天器特殊幾何特性(微分平滑、微分包含等)的軌跡規劃算法[5]。由于不滿足Brockett必要條件，欠驅動航天器不存在定常光滑的姿態穩定控制器[6]。目前，針對欠驅動控制系統設計的閉環穩定控制器主要有間斷反饋控制器、時變穩定控制器、混合控制器和最優控制器四種。其中：反饋控制法通過非奇異坐標變換求解非線性問題，主要用于原系統可實現狀態反饋的情況；時變穩定控制法通過參數在一定范圍內變化實現控制系統的收斂，用于系統參數實時可測的情況；混合控制法結合多種線性控制，通過控制器的切換實現對魯棒性要求不高的系統控制；最優控制法通過構建一個特定的性能指標，求該指標極值求解控制器，主要用于非線性較弱的系統[7-11]。欠驅動航天器閉環姿態穩定控制器主要有不連續定常狀態反饋控制器和連續時變狀態反饋控制器兩大類[12]。本文對用于欠驅動航天器的姿態控制方法進行了研究，設計了一種分段解耦控制器。與前人方法相比，本文方法可適于多種情況下的欠驅動控制：若僅俯仰角需進行機動控制，則只用第1、2個分段控制器；若僅是滾動角需進行機動控制，則用前3個分段控制器即可；若只需偏航角進行機動，則用前5個分段控制器；若三個軸均需進行機動控制，則可用6個分段控制器。本文設計的分段控制器均為PD控制器，其形式較非線性控制方法簡單，工程中易實現。

1 欠驅動航天器數學模型

定義航天器本體坐標系三軸沿其主慣量軸方向。不考慮干擾力矩和耦合，剛體航天器的旋轉運動方程可表示為

(1)

式中：H為航天器的總角動量，且H=Iω；ω為航天器角速度，且ω=[ω1ω2ω3]T∈R3；I為航天器的慣量矩陣，且I=diag[IxIyIz] ∈R3×3(取最一般情況Ix≠Iy≠Iz)；T為執行機構輸出的控制力矩。式(1)可寫成

欠驅動航天器中無法提供三軸控制力矩。不失一般性假設欠驅動軸為z軸(即z軸上無控制力矩)，則T=[TxTy0]T。將I，ω，T代入式(1)并展開，可得

(2)

定義中間變量

(3)

則動力學方程可簡化為

(4)

式(4)即為z軸欠驅動時航天器的姿態動力學模型。其中：c3為常數；u1，u2為控制器的輸入變量。

按3-1-2轉序，姿態運動學方程為

(5)

定義控制系統狀態變量為列向量

控制器輸入u=[u1u2]T。此處：φ，θ，ψ為姿態角。由系統運動學方程和動力學方程可導出系統的狀態微分方程為

(6)

式中：A，B為系數矩陣，且

2 分段解耦控制器設計

為降低失效軸角速度對系統的影響，先實現控制系統中動力學部分的鎮定，再考慮對運動學部分進行解耦。在每個分段中設計了一個PD控制器，該控制器設計簡單，便于工程實現，且選取適當的參數后可保證系統狀態變量的漸近穩定性。

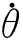
2.1 角速度鎮定

對動力學方程式(4)中的第三式求導，可得失控軸角速度分量的二階導數

(7)

設計該段控制器為

(8)

式中：k1d，k1p為控制器參數；ε為一充分小的正數，用于避免奇異。

將式(8)代入式(7)，可得

(9)

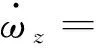
收斂為

2.2θ鎮定

該分段控制器目標是將系統的狀態變量由第一個中間狀態s1控制到第二個中間狀態

設計該段控制器為

(10)

式中：k2d,k2p為控制器參數。

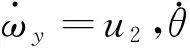
2.3φ鎮定

該分段控制器的目標是將系統的狀態變量由s2控制到第三個中間狀態

設計該段控制器為

(11)

式中：k3d,k3p為控制器參數。

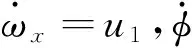
2.4θ收斂至π/2

該分段控制器的目標是將系統的狀態變量由s3控制到第四個中間狀態

設計該段控制器為

(12)

式中：k4d,k4p為控制器參數。

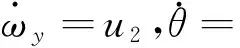
2.5ψ鎮定

該分段控制器的目標是將系統的狀態變量由s4控制到第五個中間狀態

設計該段控制器為

(13)

式中：k5d,k5p為控制器參數。

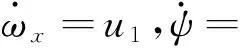
2.6θ鎮定

該分段的目標是將系統的狀態變量由s5控制到最終狀態

設計該段控制器為

(14)

式中：k6d,k6p為控制器參數。

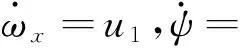
3 仿真與分析

仿真中設：航天器慣量

I=diag[1 600 1 200 1 000] kg·m2

初始姿態

[ωx(0)ωy(0)ωz(0)]T=[2 3 1] (°)/s

[φ(0)θ(0)ψ(0)]T=[30° -40° 60°]

目標姿態為航天器最終達到三軸穩定，c3=0.4，ε=0.000 1。取控制器參數k1d=0.5，k1p=0.05，k2d=0.2，k2p=0.02，k3d=0.3，k3p=0.03，k4d=0.1，k4p=0.01，k5d=0.3，k5p=0.03，k6d=0.2，k6p=0.02。用分段解耦控制器控制，當姿態角控制到目標姿態位置，誤差在0.01°內時進行控制器切換。仿真所得姿態角、姿態角速度、控制輸入和控制力矩分別如圖1～4所示。

由圖1～4可知：系統經本文設計的分段解耦控制器后能達到三軸穩定狀態。控制系統在第一個控制器作用下110 s處達到三軸角速度的鎮定，開始切換至第二個控制器；在第二個控制器作用下約170 s處將θ收斂至0，開始切換至第三個控制器；在第三個控制器作用下225s處將φ收斂至0，開始切換至第四個控制器；在第四個控制器作用下360s處將θ收斂至π/2，開始切換至第五個控制器；在第五個控制器作用下420s時將ψ收斂至0，開始切換至第六個控制器；在第六個控制器作用下480s處達到三軸穩定。

4 結束語

本文用分段解耦方法研究了欠驅動航天器的姿態機動問題。先建立航天器數學模型，由動力學和運動學方程導出控制系統的狀態微分方程。再對狀態微分方程進行分析，設計了六個分段控制器，通過控制器間的逐個切換控制，最終使控制系統狀態微分方程的狀態變量收斂至零：先通過一個非線性狀態反饋控制器，實現系統狀態微分方程中角速度部分的收斂，然后先后通過6個不同的控制器，每個控制器實現特定的控制目標，逐漸將系統狀態微分方程中歐拉角部分收斂為零，最終實現了整個控制系統的穩定。用分段解耦方法設計的控制器可實現欠驅動航天器的姿態穩定和大角度姿態控制，但也存在不可忽略的缺點。一是控制器魯棒性較差，每一步解耦的前提是此前分段控制器的控制誤差要盡量地趨近于零，對存在不可忽略的干擾力矩、非零慣量積等情況,就需為每分段設計一個魯棒控制器。二是分段解耦控制器需逐個切換設計的各個控制器，切換過程易造成姿態抖動。三是分段解耦控制的控制時間很長，無法實現姿態跟蹤，不能完成一些要求快速響應的姿態控制任務。后續，需對存在干擾力矩、耦合情況下的欠驅動航天器的控制，以及分段解耦控制器控制效率的提高進行研究。

[1] 林壯. 欠驅動水平機械臂滑模變結構控制研究[D]. 哈爾濱: 哈爾濱工程大學, 2007: 25-45.

[2] 莊宇飛. 帶有非完整約束的欠驅動航天器控制方法研究[D]. 哈爾濱: 哈爾濱工業大學, 2012: 2-14.

[3] CROUEH P E. Spacecraft attitude control and stabilization: application of geometric control theory to rigid body models[J]. IEEE Transactions on Automatic Control, 1984, 29(4): 87-95.

[4] 戈新生, 陳立群, 劉延柱. 欠驅動剛體航天器姿態運動規劃遺傳算法[J]. 動力學與控制學報, 2004, 2(2): 53-57.

[5] TSIOTEAS P, LUO J. Control of underactuated spacecraft with bounded input[J]. Automatical, 2000, 36(8): 1153-1169.

[6] BROCKETT R W. A symptotic stability and feedback stabilization[J]. Differential Geometric Control Theory, 1983: 181-191.

[7] 金磊, 徐世杰. 帶有兩個飛輪的欠驅動航天器姿態穩定控制研究[J]. 中國空間科學技術, 2009, 29(2): 8-16.

[8] POPESCU M, DUMITRACHE A. Stabilization of feedback control and stabilizability optimal solution for nonlinear quadratic problems[J]. Communications in Nonlinear Science and Numerical Simulation, 2011, 16: 2319-2327.

[9] 胡兵, 戈新生. 欠驅動航天器姿態穩定的非線性控制[J]. 北京機械工業學院學報, 2009, 24(1): 12-16.

[10] 劉海穎, 王惠南, 陳志明, 等. 基于(w,z)參數化的欠驅動微小衛星姿態再定位控制[J]. 動力學與控制學報, 2008, 6(1): 14-18.

[11] 劉楊, 郭晨, 沈智鵬， 等. 欠驅動船舶路徑跟蹤的神經網絡穩定自適應控制[J]. 控制理論與應用, 2010, 27(2): 169-174.

[12] XU R, Sliding mode control of a class of underactuated systems[J]. Automatical, 2008, 44: 233-241.

Study on Attitude Control Method of Under-Actuated Spacecraft

LIU Mei-shi, WU Jing-yu, WANG Wen-yan, YANG Sheng-qing

(Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China)

The attitude control of under-actuated spacecraft was studied in this paper. The subsection decoupling controller which could be suitable for various conditions was designed, which solved the difference of input and output dimension of the control system by using subsection decoupling method. The state differential equation of the attitude control system was established by coupling items in dynamic equation. To reduce the effect of angular velocity of failure axis on the system, first the dynamic parts in the control system were stabilized, and then the kinematic parts were decoupled. A PD controller was designed in each subsection, which had total six controllers for angular velocity stabilization, pitch angle stabilization, roll angle stabilization, pitch angle convergence to π/2, yaw angle stabilization and three-axis stabilization. By switching the controller one by one, the state variables in the state differential equation were converged to zero. So the attitude control system could be asymptomatic stabilized. The numerical simulation proved the effectiveness of the control algorithm designed. The design of the controller was simple and easy to realize in engineering. The asymptomatic stabilization of the state variables of the system would be guaranteed after the applicable parameters having been selected.

under-actuated spacecraft; attitude control; subsection decoupling; dimension; coupling; differential equation; switch control; asymptotically stability

1006-1630(2017)02-0106-06

2015-07-14；

2017-02-28

上海市青年科技啟明星計劃資助(17QB1401400)

劉美師(1991—)，男，碩士，主要研究方向為航天器姿態控制。

V448.2

A

10.19328/j.cnki.1006-1630.2017.02.011