基于自適應滑模的側窗制導控制一體化設計研究

沈昱恒,邱吉爾,張 迪,蔡云澤

(1.上海機電工程研究所,上海 201109; 2.上海交通大學 系統控制與信息處理教育部重點實驗室,上海 200240)

?

基于自適應滑模的側窗制導控制一體化設計研究

沈昱恒1,邱吉爾2,張 迪1,蔡云澤2

(1.上海機電工程研究所,上海 201109; 2.上海交通大學 系統控制與信息處理教育部重點實驗室,上海 200240)

針對側窗導彈末制導問題，提出了一種側窗探測視場約束條件下的制導控制一體化設計方法。基于彈目相對運動模型分析了側窗導彈運動規律，建立側窗導引頭探測視場角范圍與導彈姿態角的約束關系，采用基于滑模控制理論的反步法設計導彈的制導控制一體化模型，給出了自適應滑模制導律：根據姿態角與側窗視線角的約束關系，切換選擇含約束和不含約束的自適應滑模控制。控制策略為：當彈目視線不滿足側窗探測范圍約束時，在控制量中加入自適應俯仰角補償項，使目標始終處于導彈側窗視線范圍內，解決了側窗末制導過程中存在的目標跟蹤視場角不對稱約束問題；當彈目視線滿足側窗探測范圍約束時，控制無需引入姿態角約束項，可直接應用自適應滑模控制律。仿真結果表明：在末制導過程中目標始終處在側窗范圍內，且對不同的初始條件有較好的魯棒性。

側窗導彈； 末制導； 制導控制一體化設計； 反步法； 自適應滑模； 彈目視線； 側窗視線范圍； 俯仰角補償

0 引言

攔截彈高速飛行時與大氣相互作用，在其周圍形成復雜的流動結構產生的氣動加熱，使紅外導引頭探測到的目標圖像出現偏移、模糊和抖動等問題，嚴重影響探測制導精度[1]。因此，美國THAAD系統中攔截彈導引頭采用側窗模式，有效減小了氣動熱影響，但同時單側窗視場也限制了導引頭的視線范圍，導彈需實時調整彈道、導彈姿態，使目標始終在導引頭探測視場內。在末制導過程中，經典方法是將制導與姿態控制分開設計，將姿態控制作為一階延遲系統或固定時延，但側窗約束的加入對導彈姿態角控制及控制響應時間提出更高的要求，因此一種可選的研究思路是考慮將導引和控制進行一體化設計[2-3]。

近年來，導彈制導和控制一體化問題引起了研究者的注意，但多數研究重點是改善姿態控制回路的響應時間，對側窗提出的實時姿態角約束并未涉及[4]。文獻[5]在制導控制一體化模型的基礎上，采用零化脫靶量(ZEM)作為滑模面設計制導律；文獻[6]采用反步法設計制導控制律，由在線神經網絡估計系統的不確定性。在側窗導彈研究中，文獻[7]對側窗約束建模，通過導彈滾轉使目標在側窗范圍內，并通過調整俯仰角和偏航角使目標在側窗最佳視線角，但該文仍是基于傳統的設計方法將制導與姿態控制分開設計；文獻[8]在將側窗約束定義為攻角和側滑角約束的基礎上，研究了末制導中的制導控制問題，但該文設計制導律時僅考慮了終端視線角約束。為使導彈在末制導過程中能保證目標始終在側窗范圍內且命中目標，本文采用制導控制一體化設計理念，在分析建立側窗視線約束與彈體姿態運動關系的基礎上，采用自適應滑模和反步法，對一種滿足側窗姿態角約束的制導控制律設計進行了研究，并根據姿態角與側窗視線角的約束關系，切換選擇含約束和不含約束的自適應滑模控制，用末制導段數字仿真驗證本文設計方法的有效性。

1 彈目相對運動模型

傳統的導彈制導和控制系統是基于控制回路的時間常數要大于制導回路，從而將制導回路與控制回路分開設計：先根據彈目相對運動設計制導律，再設計姿態控制系統，使導彈的加速度跟上制導律，若整體的性能無法滿足期望的要求，則重新設計。在側窗探測末制導過程中，需實時快速調整彈道與姿態，分離設計造成的時延過大已不能滿足要求，因此本文考慮采用制導控制一體化設計。

制導和控制一體化設計思路是對導引回路與姿態控制回路采用聯合設計，在原理設計中，仍可在俯仰和偏航兩個平面內分別進行，本文首先考慮俯仰平面內的設計。俯仰平面內彈目相對運動關系如圖1所示。

根據文獻[5]，導彈在俯仰平面導引控制一體化模型可描述為

(1)

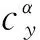
2 側窗視線約束

為描述側窗條件下導引頭對目標的探測，定義彈體坐標系OV-XVYVZV、地面坐標系O-XYZ和側窗坐標系OC-XCYCZC[8]。

a)O-XYZ系：原點O為地面發射點；OX軸在水平面內指向目標在地面的投影為正；OY軸與地面垂直向上為正。

b)OV-XVYVZV系：原點OV在導彈質心；OVXV軸與彈體縱軸重合，指向頭部為正；OVYV軸在彈體縱對稱平面內，垂直于OVXV軸；OVZV軸與OVXV、OVYV軸構成右手系。

c)OC-XCYCZC系:原點OC在導彈導引頭回轉中心；OCXC軸在彈體縱對稱平面，與側窗表面平行，指向彈頭為正；OCYC軸在彈體縱對稱平面，垂直于OCXC軸，向上為正；OCZC軸與OCXC、OCYC軸構成右手系。

為保證目標始終在目標的視線范圍內，導彈有一個“抬頭”或“低頭”的趨勢，其中“抬頭”模式的二維示意如圖2所示。

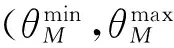
側窗視線角約束即視線角∠ACT需在(qmin，qmax)范圍內，由此要求導彈的俯仰角也在一定范圍內，兩者的轉換關系如下。

步驟1)：計算點A，C在地面系中位置

(2)

(3)

將其從側窗坐標系轉換至彈體坐標系，有

(4)

(5)

式中：σC/V為OCXC、OVXV軸的夾角；XC，YC分別為目標在側窗坐標系中的橫縱坐標；[XC0YC0]T為側窗中心在彈體坐標系中位置。

步驟2)：計算視線角和導彈姿態角的關系，有

(6)

3 自適應滑模變結構制導律設計

從上述導引控制一體化模型式(1)及側窗約束關系可知：側窗視線角約束下的制導控制問題是一個典型的高階耦合非線性控制設計問題，因此考慮采用基于滑模控制理論的反步設計法，其過程如下。

(7)

(8)

式中：

反步設計法的要點是：針對非線性系統式(7)，將其分解為不超過系統階數的子系統，然后從一個確定反饋和Lyapunov函數的子系統開始，設計中間虛擬控制量，再對虛擬控制量進行逐步修正直至全局輸入。

制導律設計通常要求x1→0。因此基于反步設計，先針對第一個子系統，定義滑模

(9)

為保證系統狀態能到達滑模面，且在達到滑模的過程中有優良的動態性能，可采用自適應趨近律

(10)

其物理意義是：當RTM較大時，適當降低趨近滑模的速率；當RTM→0時，使趨近速率迅速增大，保證視線角速率不發散[9]。

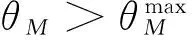
(11)

式中：p為姿態角約束的系數；ε1>0,k1>0。在式(11)中加入姿態角約束，目的是為在彈目距離接近過程中，逐漸增加姿態角約束的權重，保證目標在側窗視線范圍內。

然后針對第二個子系統，建立滑模面以保證第一個子系統的穩定

(12)

將式(11)、(12)代入第一個子系統，可得

(13)

并采用趨近律

(14)

則根據反步設計法，虛控制為

(15)

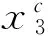
(16)

同樣采用趨近律

(17)

式中：k3>0。則可得實際的控制表達式為

(18)

對式(18)，需證明其控制穩定性。選取Lyapunov函數

(19)

由式(11)、(13)可得

ε1sgn(s1)s1-k2(s2)2-k3(s3)2<0

(20)

由此可知，設計的式(18)控制可保證系統大范圍漸進穩定。

4 仿真與分析

本部分將通過數字仿真驗證控制方法的性能。設仿真條件為：設目標和導彈的初始位置分別為RM=[0 2 200]Tm，RT=[750 1 850]Tm，速度分別為vT=900 m/s，vM=1 032 m/s；目標初始彈道傾角為0°，目標的法向加速度為5g，導彈的彈道傾角為0°；側窗的視線角范圍以OCYC軸為中心±30°，即∠ACT∈[60°，120°]；r1=10，r2=8.15，∠AMC=10°，|ωz|≤150 (°)/s，|δz|≤45°。考慮“抬頭模式”，若θmin<0°，則取θmin=0°，導彈的氣動力參數見文獻[11]。為降低滑模切換造成的控制抖振，用飽和函數

替代式(20)中符號函數sgns。此處：t=0.15。仿真所得攔截軌跡、側窗視線角和俯仰角分別如圖4～7所示。其中：圖7為導彈初始姿態角不滿足側窗約束范圍內時的姿態角變化。

由圖5可知：在整個飛行過程中，實際目標視線一直保持在側窗視線上下邊界范圍內。由圖6可知：姿態角亦始終在上下限約束范圍中。由圖7可知：即使初始姿態角不滿足側窗探測要求，本文算法也能快速作出響應保證目標在側窗范圍內。

為進一步驗證控制律的有效性和魯棒性，將本文的控制策略與文獻[10]的滑模導引律對比，進行蒙特卡羅打靶仿真。即保證其他條件相同情況下，設置以下場景。

a)場景1：導彈的初始攻角服從N(20°，(20°)2)的高斯分布，進行20次仿真驗證在不同攻角情況下算法的魯棒性。

b)場景2：目標初始位置從(750，1 850) m開始，每次間隔(50，0) m增加直至(1 200，1 850) m進行10次仿真，驗證在不同的初始彈目相對位置情況下算法的適應性。

仿真結果見表1。

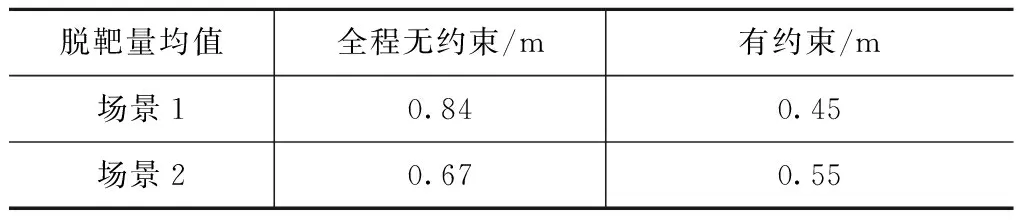
表1 有/無約束控制方法脫靶量均值Tab.1 Average miss distance of simulation between with/without constraint

由表1可知：本文設計的含姿態角約束的自適應滑模控制方法在滿足側窗約束的同時，脫靶量均值更小，精度更高。

5 結束語

導引頭側窗布局結構可有效降低紅外頭氣動加熱問題，也可作為新型多模復合導引頭提供新布局設計思路，該技術在反導、反臨近等高速、大機動目標攔截彈技術領域具有重要的工程應用價值。視場不對稱約束問題是側窗探測導彈末制導控制必須解決的問題。本文建立了導引頭側窗視線角與導彈姿態角約束關系，該方法可用于分析工程實際中各類工況彈道的側窗姿態約束關系，指導制導控制律設計；獲得了有姿態角約束的自適應滑模制導控制律。該方法采用一體化設計方法同時解決姿態角約束問題與快速性要求，仿真結果表明本文方法效果優于以往滑模制導律。本文研究可為側窗導彈制導控制方法設計提供參考。在后續研究中，可在本文基礎上對偏航通道引入后的側窗一體化制導控制問題設計進行研究，解決工程化應用問題。

[1] 江濤, 丁明松, 高鐵鎖, 等. 高速平均流場對紅外成像影響的計算分析[J]. 空氣動力學學報, 2013, 31(6): 727-732.

[2] ZARCHAN P. Tactical and strategic missile guidance[M]. St. Louis: American Institute of Aeronautics and Astronautics, 2007.

[3] HOLLOWAY J, KRSTIC M. Predictor observers for proportional navigation systems subjected to seeker delay[J]. IEEE Transactions on Control Systems Technology, 2016, 24(6): 1-14.

[4] 姚郁, 鄭天宇, 賀風華， 等. 飛行器末制導中的幾個熱點問題與挑戰[J]. 航空學報, 2015, 36(8): 2696-2716.

[5] SHIMA T, IDAN M, GOLAN O M. Sliding-mode control for integrated missile autopilot guidance[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(2): 250-260.

[6] SHARMA M, RICHARDS N D. Adaptive, integrated guidance and control for missile interceptors: AIAA Guidance, Navigation, and Control Conference and Exhibit Providence[C]// Rhode Island: 2004.

[7] 支強, 蔡遠利. 動能殺傷器側窗定向機制分析及建模[J]. 西安交通大學學報, 2012, 46(1): 91-96+113.

[8] 徐龍. 側窗探測下末制導段制導控制問題研究[D]. 哈爾濱: 哈爾濱工業大學, 2012.

[9] 周荻. 尋的導彈新型導引規律[M]. 北京: 國防工業出版社, 2002.

[10] 苗昊春, 馬清華, 陳韻, 等. 基于滑模控制的導彈制導控制一體化設計[J]. 彈箭與制導學報, 2011, 31(3): 6-10.

[11] 張保群. 導彈俯仰通道制導與控制一體化設計[D]. 哈爾濱: 哈爾濱工業大學, 2008.

Study on Integrated Guidance and Control Design for Side-Window Missile Based on Adaptive Sliding Modes

SHEN Yu-heng1, QIU Ji-er2, ZHANG Di1, CAI Yun-ze2

(1. Shanghai Electromechanical Engineering Institute, Shanghai 201109, China;2. Key Laboratory of System Control and Information Processing, Ministry of Education of China, Shanghai Jiao Tong University, Shanghai 200240, China)

An integrated design of guidance and control law under constrain of field-of-view angle (FOA) with side-window was put forward for terminal guidance of side-window missile in this paper. The motion law of the side-window missile was analyzed based on relative motion model between missile and target. The constrain of the FOA range and missile attitude angular was established. The integrated guidance and control mode was designed by the back stepping method based on sliding mode theory. The adaptive sliding mode law was given. The switching between the constrain adaptive sliding mode law and non-constrain adaptive sliding mode law was selected according to the constrain relationship of attitude angular and field-of-view angle of side-window. The control strategy was that the adaptive pitch compensation was added into the control to keep the target in the side-window range of the missile at all when the FOA of the missile and target did not meet the constrain of side-window detection range. It solved the problem of the asymmetrical constrain of target tracking FOA in the terminal guidance of side-window, and the adaptive pitch angular compensation did not need to add into the control which could apply the adaptive sliding mode law directly when the FOA of the missile and target met the constrain of side-window detection range. The numerical simulation results showed that the proposed solution could make the target in the side-window range in the terminal guidance, and it had good robustness under different initial conditions.

side-window missile; terminal guidance; integrated guidance and control design; back stepping method; adaptive sliding mode; FOA of missile and target; range of side-window; pitch compensation

1006-1630(2017)02-0061-06

2016-09-23；

2017-01-22

國家自然科學基金資助(61374160)；航空科學基金資助(20140157002)

沈昱恒(1983—)，男，博士，主要從事制導控制系統設計與研究。

TJ765.2

A

10.19328/j.cnki.1006-1630.2017.02.005