[案例]幾何輔助線項目教學例談

王偉江

一、由一般到特殊。引導學生分割圖形

在解決一些圖形面積的題中，常常需要把不規則的圖形轉化為規則的圖形，或把復雜的圖形轉化為簡單的基本圖形。一般情況下，學生對特殊圖形的面積計算是熟悉的，如直角三角形、平行四邊形、矩形、菱形、正方形、圓等。在教學過程中，教師要善于在學生已有的知識基礎上啟發引導學生思維，把一般化的圖形分割為特殊的、可計算的圖形。正如教育家陶行知所說的，“接知如接枝”。

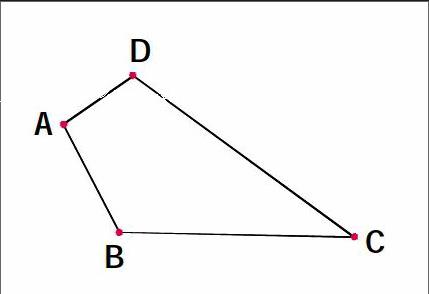
例1如圖，在四邊形ABCD中，若∠BAD=90°，AD=3，AB=4，BC=12，CD=13，求四邊形ABCD的面積。

分析：解這道題需要添加輔助線，連接BD，把四邊形的面積轉化為兩個三角形的面積之和。

引導：在讓學生思考之前，可先提問學生：“你會求哪些四邊形的面積？”學生會回答是平行四邊形、矩形、菱形、正方形。這時接著問：“你會求直角三角形的面積嗎？”“不規則的四邊形的面積怎樣求？”這樣教學，可使學生的思維變得有序、有目標，學生自然而然地會想到，要求不規則的四邊形的面積，可通過連接對角線轉化為兩個三角形的面積之和來求解。

二、把握定理題設。引導學生補全圖形

幾何證明就是從已知條件出發，經過推理得出結論。推理的依據是與條件有關的公理、定理等。解題時，公理、定理的運用都需要一定的條件，所以在教學中教師應引導學生自己正確把握公理、定理的題設，把分散的、孤立的條件聯系到一起，如果題中沒有能利用條件的圖形，就要添加一些輔助線補全圖形，以利于公理、定理等的運用。這是學生會添加輔助線證明幾何題、會思維、會學幾何的一個很好的切入點。

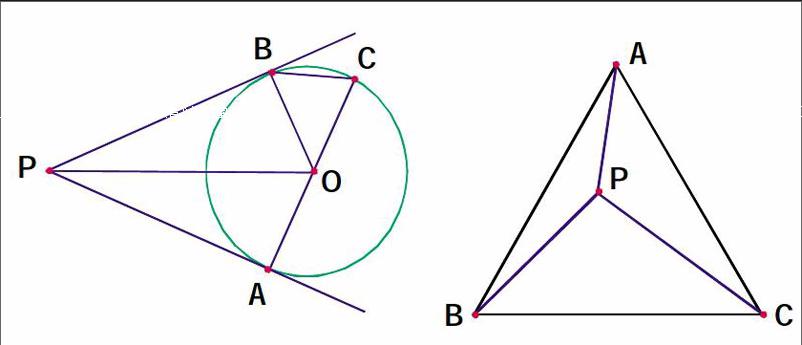
例2.已知：如圖，PA、PB是00的兩條切線，切點為A、B，Ac是（30的直徑。求證：PO∥BC。

分析：本題中主要運用切線長定理、等腰三角形三線合一定理和直徑所對圓周角是直角這三個定理。

引導：在學生思考之前，可先提問學生：“你知道與直徑有關的定理有哪幾個？”學生容易回答是垂徑定理，直徑所對圓周角是直角等。再問：“等腰三角形三線合一的條件是什么？本題中有等腰三角形嗎？”由于本題是切線長定理運用的一個例題，所以學生根據切線長定理輕松得到PA=PB，OP平分∠APB，再聯系Ac是QO的直徑這個條件，只要連接AB，就補全了等腰三角形三線合一和直徑所對圓周角兩個定理的基本圖形，運用這兩個定理易得PO與BC都與AB垂直，從而證得PO∥BC。

三、利用幾何變換。移動局部圖形

在解題時，當題目給出的條件顯得不夠或者不明顯時，可以啟發學生將圖形作一定的變換，這樣將有利于發現問題的隱含條件，抓住問題的關鍵和實質，使問題得以突破，找到滿意的解答。圖形變換是一種重要的思維方法，它是一種以變化的、運動的觀點來處理分散的、孤立的問題的思維，學生若能很好地領會這種解題方法的本質特征，并能準確合理地使用，在解題中就會收到奇效，也將有效地提高思維品質。

例3.P是等邊三角形ABC內的一點，LAPB=J50°PA=3，PB=4。求：Pc的長。

分析：所求的線段Pc與已知線段PA、PB不構成一個三角形，條件分散，不容易求得Pc的長度，由于AABC是等邊三角形，具備了旋轉角為60°的圖形旋轉條件，因此，可將AAPB以點B為旋轉中心作順時針60°的旋轉；還可將AABP以點A為頂點，逆時針旋轉60°，將AAPC繞點c逆時針旋轉60°。

引導：筆者先讓學生嘗試著解本題，在學生感到無處下手時，提問：“等邊三角形是什么對稱圖形？”學生答：“它是軸對稱圖形。”“還有呢？”學生又答：“它還是旋轉對稱圖形。”接著問：“那么它的旋轉中心在哪里？”“等邊三角形除了繞著它的中心旋轉，還能繞哪些點旋轉？”“AAPB能否繞著某個點旋轉？”到這時，學生似乎有點感悟。于是就讓學生繼續思考，再試著解本題。

在實際教學中，教師應根據具體的問題情境具體分析，讓學生在不斷地嘗試、不斷地失敗中揭示隱含在輔助線中的精彩而又獨特的思維過程，并引導學生的思維深入到知識的發現或再發現的過程中去，只有這樣，學生才能真正理解和掌握知識，并把教師所教的內容轉化為自己的智慧。誠如蘇霍姆林斯基所說的那樣：“在學生的腦力勞動中，擺在第一位的并不是背書，不是記住別人的思想，而是讓學生本人進行思考，也就是說，進行生動的創造。”