基于matlab的常見(jiàn)插值法及其應(yīng)用

郭小樂(lè)

（寧夏大學(xué) 數(shù)學(xué)統(tǒng)計(jì)學(xué)院，寧夏 銀川 750021）

基于matlab的常見(jiàn)插值法及其應(yīng)用

郭小樂(lè)

（寧夏大學(xué) 數(shù)學(xué)統(tǒng)計(jì)學(xué)院，寧夏 銀川 750021）

本文就數(shù)值分析中幾種常見(jiàn)的插值法:拉格朗日插值、牛頓插值、Hermite插值及三次樣條插值,討論其不同形式的表達(dá)式及誤差,結(jié)合matlab給出具體實(shí)例,對(duì)比分析.此外還就三次樣條插值的不同計(jì)算方法進(jìn)行歸納、總結(jié).

拉格朗日插值；牛頓插值；Hermite插值；三次樣條插值；matlab

1 引言

在許多工程問(wèn)題中,有時(shí)我們只能給出某一函數(shù)在一些離散點(diǎn)的值,給不出具體的函數(shù)表達(dá)式,或者函數(shù)的表達(dá)式過(guò)于復(fù)雜不利于計(jì)算,這時(shí)我們就需要構(gòu)造這個(gè)函數(shù)的近似函數(shù),數(shù)學(xué)上我們把這種方法稱(chēng)為插值[1].插值法作為函數(shù)逼近、數(shù)值微積分及微分方程數(shù)值解的基礎(chǔ),在當(dāng)今社會(huì)被越來(lái)越多的學(xué)者所關(guān)注.尤其隨著計(jì)算機(jī)的普及,很多學(xué)者將插值與matlab等軟件結(jié)合,使得插值法得到了更廣泛的應(yīng)用.

常用的插值法包括：拉格朗日 (Lagrange)插值、牛頓(Newton)插值、Hermite插值、三次樣條插值,本文就這四種插值法,結(jié)合matlab,從其公式的構(gòu)造、余項(xiàng)出發(fā),對(duì)不同的插值法通過(guò)數(shù)值實(shí)例進(jìn)行對(duì)比研究.此外,還就具有良好收斂性的三次樣條函數(shù),歸納出不同的計(jì)算方法.

2 幾種常見(jiàn)插值法

由于代數(shù)多項(xiàng)式具有簡(jiǎn)單和一些良好的特性,如多項(xiàng)式是無(wú)窮光滑的,容易計(jì)算它的導(dǎo)數(shù)及積分.故本文選擇代數(shù)多項(xiàng)式作為插值函數(shù).下面依次就這幾種插值法進(jìn)行討論.

2.1 Lagrange插值

所謂n次Lagrange插值即給定平面上的n+1個(gè)互不相同的插值點(diǎn)(xi,f(xi)),i=0,1,2,…,n,利用插值基函數(shù)構(gòu)造唯一的一條次數(shù)不高于n次的插值多項(xiàng)式.

2.1.1 n次Lagrange插值多項(xiàng)式形式及誤差

拉格朗日插值公式的優(yōu)點(diǎn)是格式整齊和規(guī)范,在理論分析中有重要的價(jià)值.它的缺點(diǎn)是沒(méi)有承襲性質(zhì),當(dāng)需要增加插值節(jié)點(diǎn)時(shí),需要重新計(jì)算所有的插值基函數(shù),計(jì)算繁瑣.

2.2 Newton插值

Newton插值是利用差商計(jì)算的,下面我們首先給出差商的概念.

定義1[1]設(shè)x0,x1,…，xk互不相同,f(x)關(guān)于x0,x1,…，xk的k階差商為

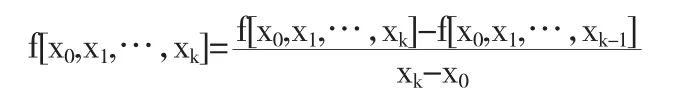
2.2.1 n次Newton插值多項(xiàng)式的形式及誤差

牛頓插值具有拉格朗日插值沒(méi)有的承襲性,當(dāng)增加插值節(jié)點(diǎn)時(shí),只需再計(jì)算一項(xiàng)即可得到相應(yīng)的插值多項(xiàng)式.由插值多項(xiàng)式的唯一性可知二者是同一插值多項(xiàng)式的不同表達(dá)形式.

2.3 Hermite插值

常用Hermite插值描述如下[1]：對(duì)于f(x)具有一階連續(xù)導(dǎo)數(shù),以及插值點(diǎn)xi,i=0,1,…,n,xi互不相同,若有至多為2n+1次的多項(xiàng)式函數(shù)H2n+1(x)滿足：

則稱(chēng)H2n+1(x)為f(x)關(guān)于節(jié)點(diǎn){xi}ni=0的Hermite插值多項(xiàng)式.

2.3.1 Hermite插值多項(xiàng)式的形式及誤差:

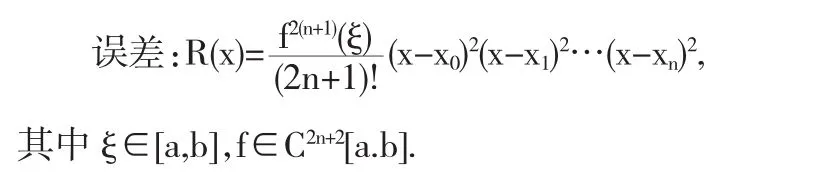
2.4 三次樣條插值

在實(shí)際計(jì)算中,人們很少采用高次插值,其主要原因有兩個(gè):其一,由于受到所要通過(guò)的插值節(jié)點(diǎn)的約束,高次插值描繪的代數(shù)曲線是擺動(dòng)的.即我們常說(shuō)的Runge(龍格)現(xiàn)象;其二,從計(jì)算的舍入誤差看,對(duì)于等距結(jié)點(diǎn)的差分形式,結(jié)點(diǎn)上函數(shù)值的微小變化可能導(dǎo)致高階差分的很大變動(dòng).故在應(yīng)用中主要采用的是分段低次插值.實(shí)踐證明,用分段的低次插值多項(xiàng)式逼近被插函數(shù)比在全區(qū)間上用高次插值多項(xiàng)式效果好.

一般來(lái)說(shuō),分段插值所描繪的曲線是不光滑的.為了能獲得一條足夠光滑的插值曲線,近年來(lái)人們采用了分段多項(xiàng)式光滑插值法,即著名的樣條函數(shù)插值法.本文我們主要介紹具有良好的收斂性,具有二階光滑性的三次樣條插值.

2.4.1 三次樣條函數(shù)

定義2[5]給定[a,b]上n+1個(gè)節(jié)點(diǎn)a=x0＜x1＜…＜xn-1＜xn=b以及這些點(diǎn)上的函數(shù)值f(xi)=yi(i=0,1,…,n).若函數(shù)s(x)滿足:

（1）s(xi)=yi,i=0,1,2,…,n；

（2）在每個(gè)小區(qū)間[xi,xi+1]上是一個(gè)次數(shù)不超過(guò)三次的多項(xiàng)式；

（3）s(x)、s'(x)、s"(x)在[a,b]上都連續(xù).

則稱(chēng)s(x)為函數(shù)f(x)關(guān)于節(jié)點(diǎn)x0,x1,…,xn的三次樣條函數(shù).

2.4.2 三次樣條插值的幾種計(jì)算方法

2.4.2.1 利用二階導(dǎo)數(shù)為線性函數(shù)求解

令s"(xj)=Mj,j=0,1,…,n.因?yàn)閟(x)為分段三次多項(xiàng)式,故s"(x)在[xj,xj+1]上是線性函數(shù).可表示為

其中hj=xj+1-xj

為了求出s(x)在[xj,xj+1]上的表達(dá)式,需要對(duì)上式積分兩次,并利用s(xj)=yi及s(xj+1)=yj+1可求出積分常數(shù).得三次樣條函數(shù)表達(dá)式:

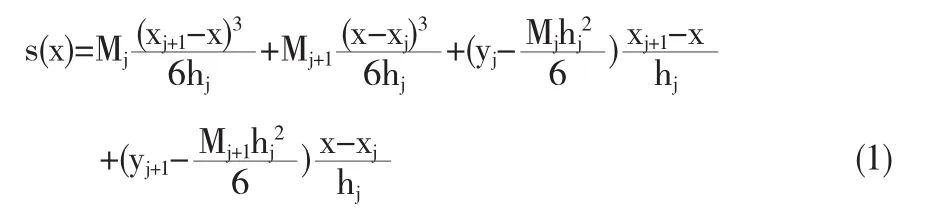
再利用光滑連接條件s'(xj-0)=s'(xj+0)，并對(duì)s(x)求導(dǎo)得

為了確定唯一的Mj(j=0,1,…,N),補(bǔ)充三個(gè)邊界條件:

（1）假定s'(x0)=f'0，s'(xn)=f'n；

（2）假定 s"(x0)=f"(x0)，s"(xn)=f"(xn)直接得端點(diǎn)方程M0=f"0，Mn=f"n；

（3）假定M0=MN=0,即為自然邊界條件,可得M0=Mn，λnM1+μnMn-1+2Mn=dn；

以上三個(gè)邊界條件將其寫(xiě)成矩陣形式,得關(guān)于Mj(j=0,1,…,n)的三對(duì)角線性方程組,利用追趕法[2]求出唯一的Mj(j=0, 1,…,n),將其代入s(x)即可.

2.4.2.2 利用特殊形式的埃爾米特插值公式求解

若插值節(jié)點(diǎn)取為xk,xk+1,插值多項(xiàng)式為H3(x),則采用基函數(shù)法,

令H3(x)=αk(x)yk+αk+1yk+1+βk(x)mk+βk+1(x)mk+1

其中αk(x)，αk+1（x），βk(x)，βk+1(x)是關(guān)于插值節(jié)點(diǎn) xk，xk+1的三次Hermite插值基函數(shù).

上式即為由特殊的埃爾米特插值公式推導(dǎo)的三次樣條插值的計(jì)算方法之一.

3 數(shù)值實(shí)例

下圖是利用matlab(2012b)編程軟件繪制的上述條件下四種不同算法在[0.25,4]插值函數(shù)曲線圖(a)及其相對(duì)誤差曲線圖(b),直觀明了地展示不同插值算法的效果.

圖a 插值函數(shù)曲線圖

從圖a中可看出不同插值方法對(duì)原函數(shù)的逼近效果相差不大.但從圖b中的不同插值法的相對(duì)誤差大小可知,這四種插值方法中,Lagrange插值和Newton插值的效果是一樣的,相對(duì)另外兩種插值方法來(lái)說(shuō),這兩種方法的逼近效果較差,其次是Hermite插值的逼近效果較好,而具有良好收斂性及二階光滑性的三次樣條插值來(lái)說(shuō),其誤差最小,逼近效果最好.

圖b 相對(duì)誤差曲線圖

4 總結(jié)

本文根據(jù)運(yùn)用的插值條件的不同,對(duì)《數(shù)值分析》中常用的四種插值法進(jìn)行歸納總結(jié).通過(guò)具體的數(shù)值實(shí)例,結(jié)合matlab編程軟件,通過(guò)圖像直觀明了地展示不同方法的逼近效果,還繪制了不同插值方法的相對(duì)誤差曲線圖,從誤差的角度分析不同方法的效果.為不同領(lǐng)域的科研工作者提供理論基礎(chǔ).

〔1〕張韻華,奚梅成,陳效群.數(shù)值計(jì)算方法與算法[M].北京：科學(xué)出版社,2006.

〔2〕李慶揚(yáng),王超能,易大義.數(shù)值分析（第五版）[M].北京：清華大學(xué)出版社,2008.

〔3〕徐利治,周蘊(yùn)時(shí),孫玉柏.逼近論[M].北京：國(guó)防工業(yè)出版社,1985.

〔4〕呂曉亞,張莉.插值法在數(shù)值分析中的教學(xué)實(shí)踐[J].唐山師范學(xué)院學(xué)報(bào),2011,33(2):123-125.

〔5〕張希娜,李亞紅,郭中凱.關(guān)于三次樣條插值的教學(xué)研究[J].長(zhǎng)沙大學(xué)學(xué)報(bào),2012,26(2):131-132.

〔6〕張麗娟.三種插值方法的應(yīng)用與比較[J].赤峰學(xué)院學(xué)報(bào)(自然科學(xué)版),2010,26(3):1-3.

〔7〕林昌華,楊巖.拉格朗日插值法在工程設(shè)計(jì)及CAD中的應(yīng)用[J].重慶理工大學(xué)學(xué)報(bào)(自然科學(xué)版),2013,27(12):34-37.

O241.3

A

1673-260X（2017）04-0005-03

2017-01-25