我國城市空氣污染數據的準確性判別研究
——基于我國東部三大城市群的比較分析

湯潔茹，董 瑤，蓋伊蕾

（1.安徽財經大學 金融學院；2.安徽財經大學 統計與應用數學學院，安徽 蚌埠 233030）

我國城市空氣污染數據的準確性判別研究
——基于我國東部三大城市群的比較分析

湯潔茹1，董 瑤2，蓋伊蕾2

（1.安徽財經大學 金融學院；2.安徽財經大學 統計與應用數學學院，安徽 蚌埠 233030）

本文針對城市空氣污染數據的真實性判別及分析問題，以多元線性回歸、主成分分析、參數估計、相關分析為研究手段與方法，通過建立多元線性回歸模型、各城市群氣象數據真實性判定模型、雙變量相關分析等模型，得出以下結論：（1）東部三大城市群中，京津冀城市群空氣污染數據的準確度低于珠三角與長三角，這可能是由于京津冀極端天氣情況較多造成的后果；（2）工業產值與空氣質量指標AQI指數、PM2.5、PM10較強的相關性.

城市空氣污染；主成分分析；MATLAB；數據分析誤判

空氣質量問題始終是政府、環境保護部門和全國人民關注的熱點問題.2016年的兩會上,全國政協常委、環境保護部副部長吳曉青表示，政府工作報告中提出今后五年地級市及以上城市空氣質量優良天數比率超過80%的目標必須完成.然而，由于各種主客觀原因，會使所采集到的數據序列體現出一定的異常、造假現象.因此對空氣污染數據真實性的研究具有一定的現實意義.

1 數據來源與模型假設

京津冀、長三角、珠三角城市群2013年11月1日到2015年2月28日的相關空氣污染數據以及蘇州市工業產值數據.為了便于解決問題，提出以下假設：(1)假設除了空氣污染物含量沒有其他因素影響AQI；(2)假設極端天氣對空氣污染物含量不存在影響；(3)假設若空氣污染數據真實，則數據是連續的；(4)假設加入社會因素時，空氣質量僅受這一社會因素影響；(5)假設查詢的有關城市群社會因素數據是真實有效.

2 空氣質量真實性分析

2.1 研究思路

首先我們繪制2015年1月2日到2015年2月28日這一時間段三個城市群AQI指數的變化折線圖以判斷各城市群AQI指數分布是否一致，若該城市群各指數在同一時刻差異較大則該城市群數據存在誤差（或偏誤）的現象可能較嚴重.再以PM10為被解釋變量其他指標為解釋變量對三個城市群所有城市進行多元線性回歸，最后根據線性回歸的結果選取殘差平方和較大城市.

2.2 數據處理

基于所給數據我們選取2015年1月2日到2015年2月28日這一時間段三個城市群（京津翼、長三角、珠三角城市群）AQI指數的數據，利用MATLAB繪制AQI指數變化折線圖，結果如圖1、圖2、圖3所示.

從圖2、圖3、圖4中可以看出京津翼城市群各城市之間AQI指數變化差異較大而長三角城市群和珠三角城市群各城市在這一時段AQI指數波動情況相似且AQI數值較為靠近.因此我們初步判斷，京津翼城市群空氣質量數據誤判的情況相對于其他城市要嚴重.

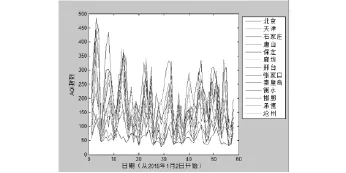
圖1 京津翼城市群AQI指數變化折線圖

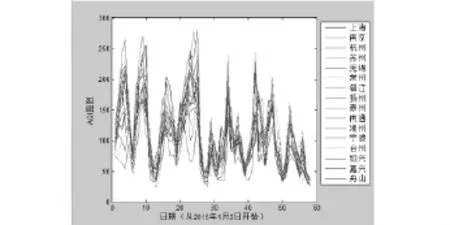
圖2 長三角城市群AQI指數變化折線圖

以京津翼城市群所有城市不同日期的空氣污染數據作為隨機變量的原始數據計算相關系數.設變量y、x1、x2、x3、x4、x5分別為 AQI指數、PM2.5濃度、PM10濃度、CO濃度、NO2濃度、SO2濃度，利用EVIEWS得到的相關系數矩陣，如圖4.

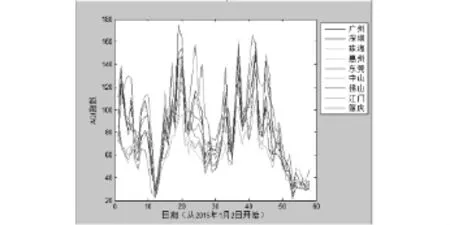
圖3 珠三角城市群AQI指數變化折線圖

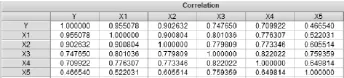
圖4 各變量之間的相關系數矩陣

由圖4可知，x2與其余變量的相關性較高均在0.5以上，因此，個地方部門在對數據的誤判最有可能是對x2代表的PM10數值進行了錯誤測算（或者由于極端天氣造成數據統計偏誤）.

以PM10濃度被解釋變量，PM2.5濃度、CO濃度、NO2濃度等指標作為解釋變量進行多元線性回歸并得到相應的誤差平方和，如表1.

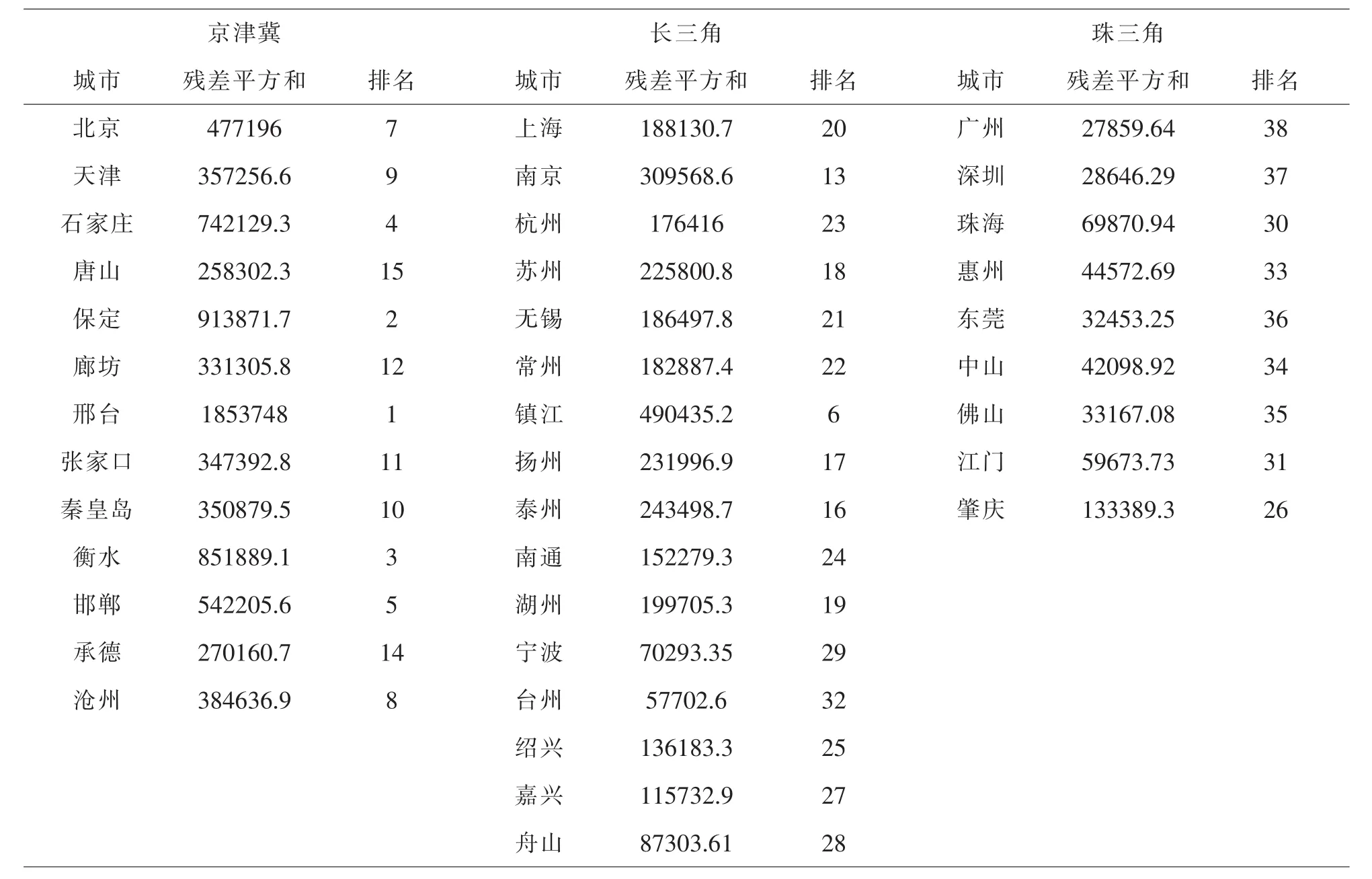
表1 各地回歸殘差平方和及排名表

2.3 結果分析

由表1可知北京、天津、保定、衡水等城市群殘差平方和較大分別為477196、357256.6、913871.7、851889.1，相對于其他城市群的對這些城市群進行多元線性回歸時效果并不理想，有可能是由于地方政府獲取的PM10數據存在較大誤差使x1、x3、x4、x5對x2解釋效果變差.

3 各污染物的相關性分析

3.1 研究思路

首先，通過主成分分析選取能夠涵蓋各污染物所含信息的變量，選取PM2.5,PM10作為主成分，方差累計貢獻率可達到91.34%；其次，計算各城市群PM2.5與PM10的相關系數；然后，對這些相關系數進行正態性檢驗，證明這些相關系數服從正態分布.則在99.73%的置信度下，計算這些相關系數的置信區間，若該城市群的主成分的相關系數不在置信區間內，則說明該城市群數據的真實性或者準確性不足.

3.2 數據處理

毫無疑義，空氣的主要污染物變量之間是具有一定的相關關系的.因此，在各個變量之間相關關系研究的基礎上，利用主成分分析用較少的新變量代替原來較多的變量，而且使這些較少的新變量盡可能多地保留原來較多的變量所反映的信息.

對各污染物指標變量進行主成分分析：

表2 KMO and Bartlett's檢驗

由表2可知，各污染物指標變量適合做主成分分析

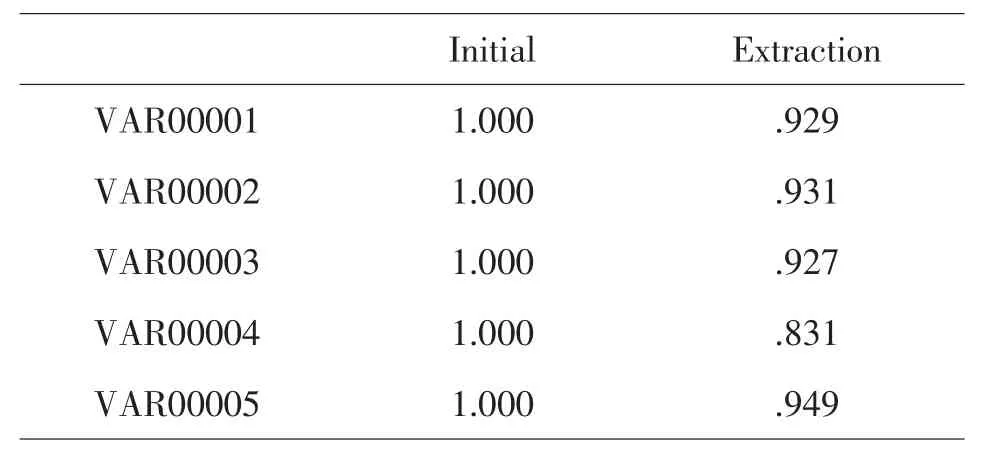
表3 Communalities分析

由表3、表4可知，為使累計方差貢獻率達到85%以上，選取PM2.5和PM10作為主成分，則累計方差率可達到91.343%.

計算各城市群的PM2.5與PM10的相關系數

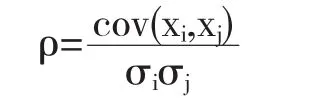
則可得到各城市群PM2.5和PM10的相關系數，結果見表5.

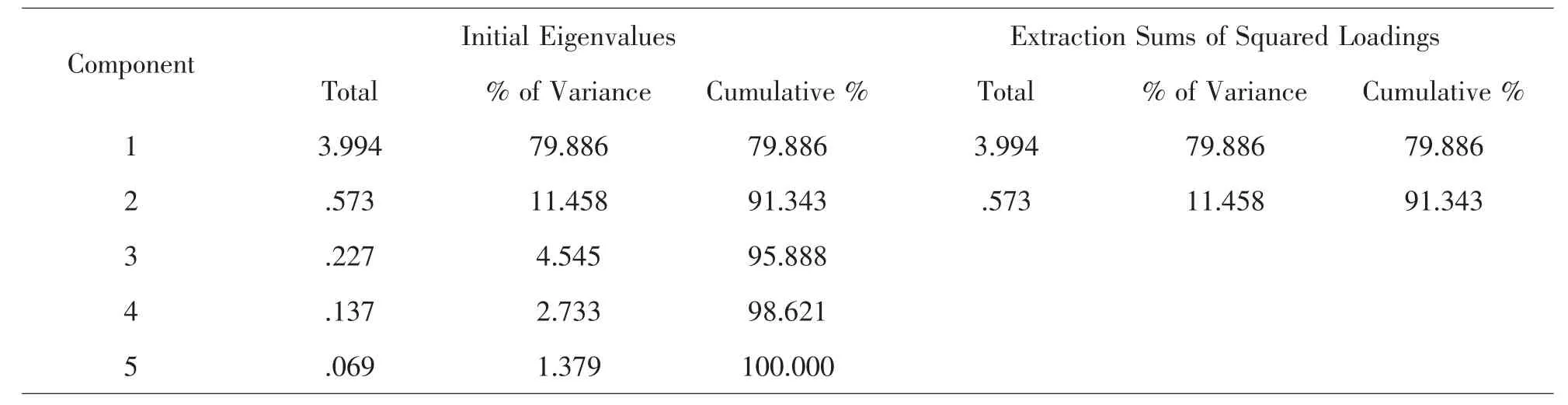
表4 各變量累計貢獻率表

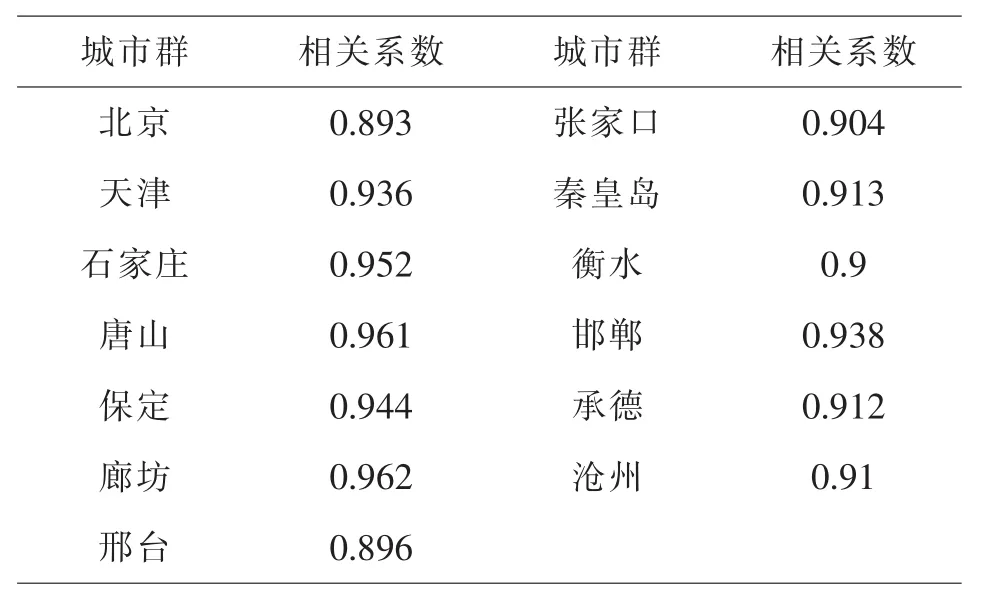
表5 各城市群PM2.5和PM10的相關系數表

將這一列相關系數基于SPSS進行正態性檢驗，結果見表6.

由表6可知，sig值大于0.05，則接受原假設，即這列數據服從正態分布.

3.3 結果分析

這列數據服從正態分布，從而可以計算置信區間.

在置信水平為99.73%下，概率度z=3

表6 Tests of Normality

計算抽樣極限誤差Δx=zσx=3×0.00694=0.02

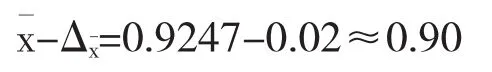
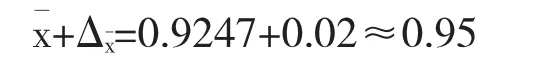
在99.73%的置信度下，置信區間為[0.9，0.95]，則可知北京，石家莊，唐山，濰坊，邢臺城市群的空氣質量數據存在不準確的現象.

4 空氣質量與工業生產相關性分析

4.1 研究思路

首先我們從蘇州市統計局得到蘇州市2014年各月的工業產值.其次對數據進行了篩選，由前兩問得到的結果我們發現許多工業發達的城市群，都存在信息造假的情況，所以我們選擇蘇州市的數據進行分析.然后對數據進行處理，取得蘇州市2014年各月的工業產值平均值和蘇州市2014年各月空氣污染指標數據的平均值.最后運用SPSS對變量做雙變量相關性分析.

4.2 數據處理

獲取數據，對數據進行處理，得到的數據見表7.

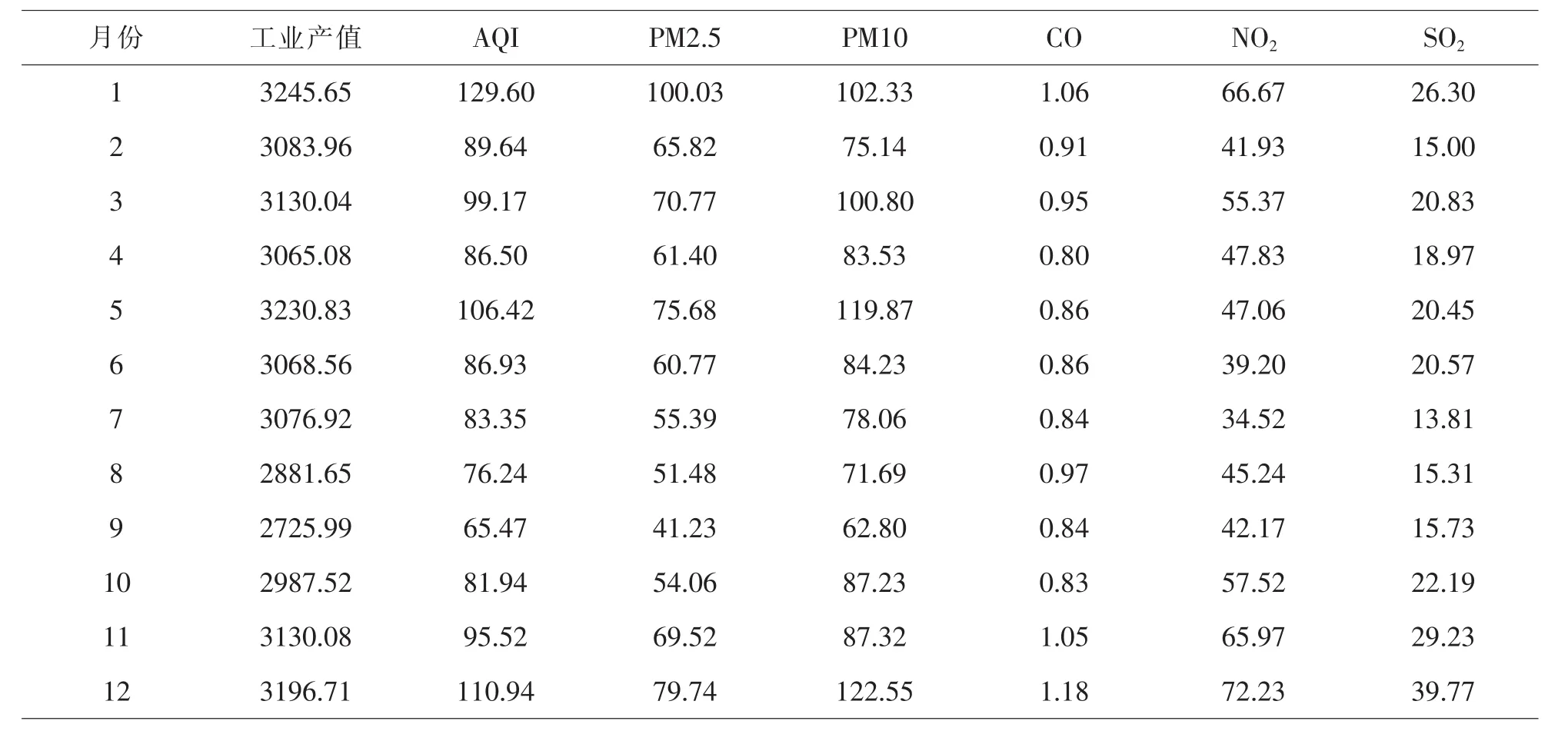
表7 蘇州市2014年各月工業產值和空氣污染數據平均值表

4.3 結果分析

運用SPSS軟件得到兩兩變量的相關系數，見表8.

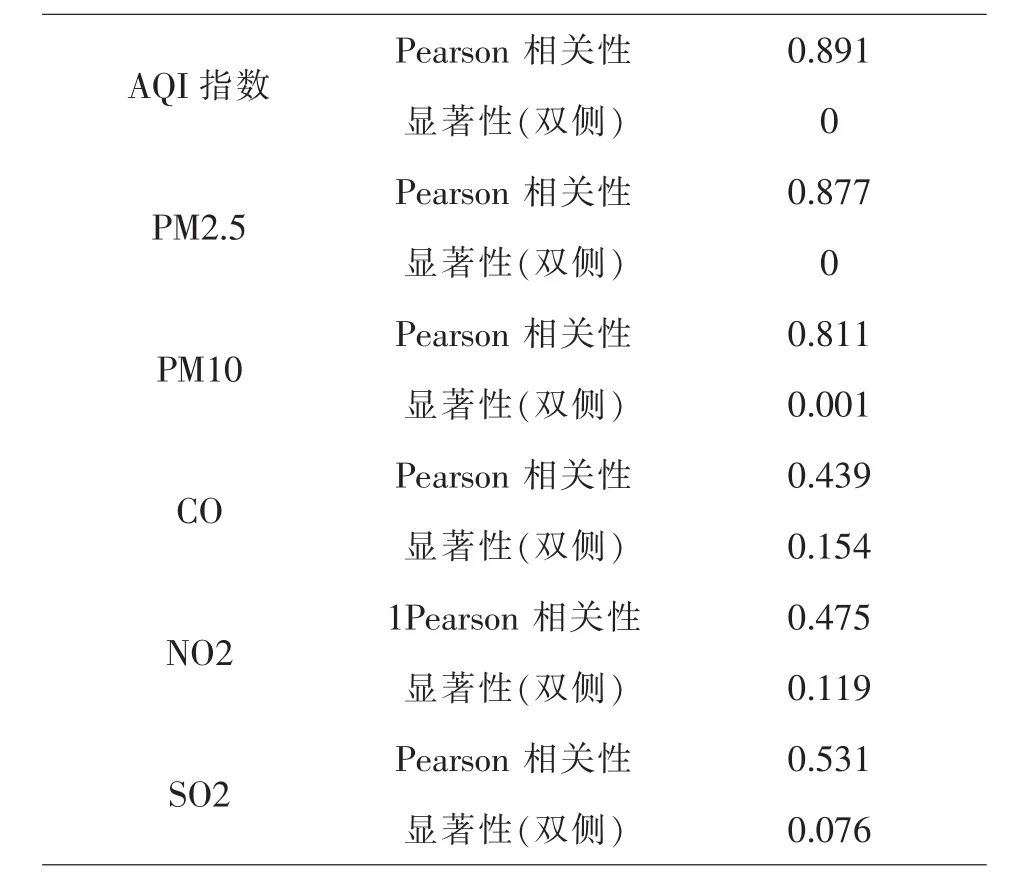
表8 與工業產值相關性分析結果表

由表8可知，AQI、PM2.5、PM10與工業產值的相關系數均接近1，且顯著性小于0.05，說明AQI、PM2.5、PM10與工業產值具有很強的相關性.

5 總結

如前所述，研究分析得出，在東部三大城市群中，京津冀城市群空氣污染數據的準確度低于珠三角與長三角，這可能是由于京津冀極端天氣情況較多造成的后果；與此同時，工業產值與空氣質量指標AQI指數、PM2.5、PM10較強的相關性.研究認為，針對有關空氣污染數據的準確性問題,綜合使用量多種模型和統計方法進行研究,使問題得到更加全面分析,綜合使用EVIEWS、SPSS等軟件得出各污染數據、工業生產數據的相關性，很好地解決了空氣污染數據的準確性判別問題.

〔1〕薛志誠,藺相如.多元統計分析在評估城市空氣污染中的運用[J].電力學報,2009(2):152—153.

〔2〕司守奎,孫璽菁.數學建模算法與應用[M].北京：國防工業出版社，2015.9.

〔3〕吳禮斌，等.經濟數學與建模（第二版）[M].北京：國防工業出版社，2013.6.

X51；O13

A

1673-260X（2017）04-0001-04

2016-12-09