白雪公主和七個小矮人
——記與拋物線有關的七個圓

吳笑蓬

江蘇省海門中學高二(5)班 (226100)

白雪公主和七個小矮人
——記與拋物線有關的七個圓

吳笑蓬

江蘇省海門中學高二(5)班 (226100)

在近幾年江蘇高考的附加試題中，以與拋物線有關的軌跡類問題作為壓軸的頻率較高.想在這樣類型的題目上順利過關，進而取得較為滿意的分數，取決于給的時間的多少.如果掌握了與拋物線相關的一些結論，那么解決這樣類型的問題也就事半功倍了.筆者結合老師上課的講解以及自己在平時學習中的感悟，發現了拋物線中的“七個小矮人”這樣有趣的現象，希望對大家有所啟發.

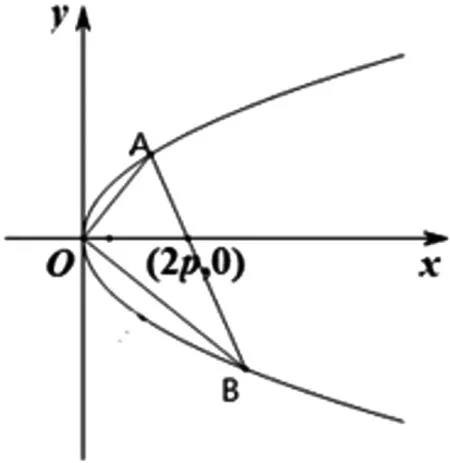
圖1

圓一：過x軸上一點M(2p,0)作拋物線y2=2px(p>0)的任意一條弦，則以其弦為直徑的圓必過原點.

證明：不妨設弦AB的方程：x=my+2p,聯立拋物線方程得到

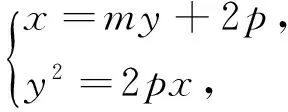
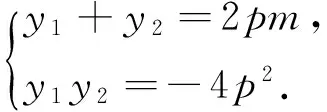
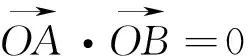
在對圓1的研究過程中又發現了這樣的一個逆命題:如圖1，OA與OB為拋物線y2=2px(p>0)相互垂直的兩條弦，連AB,則直線AB恒過H(2p,0).(OH的一個靠近O的四等分點即為拋物線的焦點),這樣的結論也有利于我們快速準確的確定拋物線的焦點所在位置.

圓二：若AB為y2=2px(p>0)的焦點弦，過A,B分別作準線的垂線，垂足為A1,B1,則以AB為直徑的圓與A1B1相切.

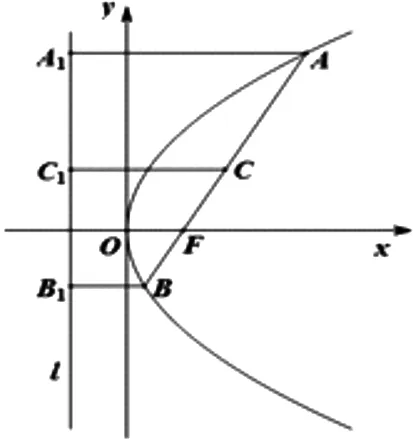
圖2

將焦點弦與準線結合在一起,竟有這么奇妙的性質,那讓我們在下一題中繼續展開豐富的想象吧!

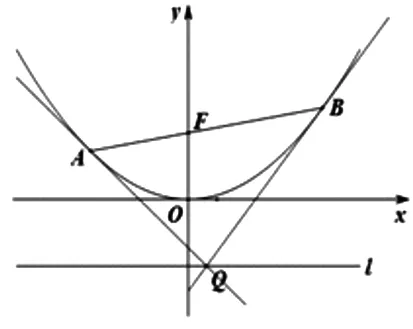
圖3

(理)(2011韶關月考)已知動圓過定點F(0,2)，且與定直線l:y=-2相切.

(1)求動圓圓心的軌跡C的方程；

(2)若AB是軌跡C的動弦，且AB過F(0,2)，分別以A,B為切點作軌跡C的切線，設兩切線的交點為Q，證明：AQ⊥BQ.

原題的解答如下:

(1)易知圓心的軌跡是x2=8y.

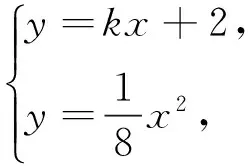
既然AQ⊥BQ，我們就能想到點Q就在以AB為直徑的圓上，就可以大膽猜測一般情況下以AB為直徑的圓與準線相切.即得出圓二：以AB為直徑的圓與A1B1相切.反之如果我們利用圓2的相關結論也能迅速解決該題的第二問，甚至還可以推出Q在定直線y=-2上(當然此處還用到在拋物線A處的切線平分∠FAA1這樣的結論).

以AB為直徑的圓與A1B1相切，那么將AB與A1B1交換位置即以A1B1為直徑的圓又有什么特點呢?是否與AB相切呢？將AB截成兩段變成AF,BF，分別以AF,BF為直徑作圓，是否也會有什么特殊的性質呢？請看以下探究.

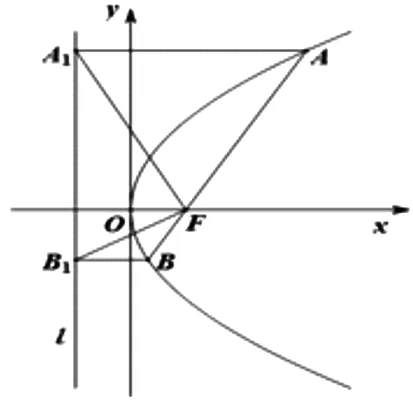
圖4

圓三：若AB為y2=2px(p>0)的焦點弦，過A,B分別作準線的垂線，垂足為A1,B1,則以A1B1為直徑的圓與AB相切.

證明:如圖4,AA1∥x軸?∠AA1F=∠A1FO,AF=AA1?△AFA1中，∠AA1F=∠A1FA?∠A1FA=∠AA1F=∠A1FO.同理

∠OFB1=∠BFB1?∠A1FO+∠A1FA+∠OFB1+∠BFB1=π,∴2(∠A1FO+∠OFB1)=π?

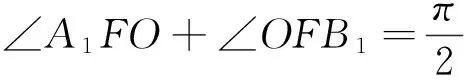
圓四(五)：若AB為y2=2px(p>0)的焦點弦，過A,B分別作準線的垂線，垂足為A1,B1,F為焦點，C1為A1B1的中點，則BB1C1F四點共圓(AA1C1F四點共圓).

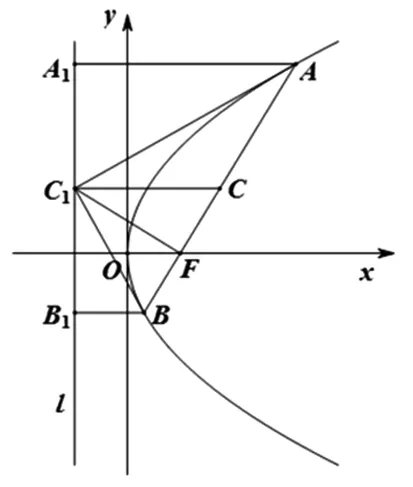
圖5

證明：如圖5,取AB中點C,∵CC1=BC,∴∠CC1B=∠CBC1,又∵CC1∥BB1,∴∠CC1B=∠B1BC1,

∴∠C1BB1=∠CBC1,

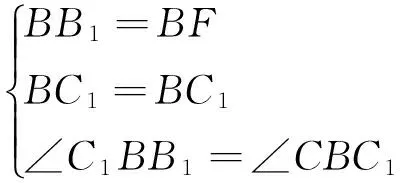
△BB1C1?△BFC1?

B1C1⊥BB1,C1F⊥BF, ?BB1C1F四點共圓.

同理AA1C1F四點共圓.

圖6

帶著這樣的結論,我們再來欣賞2017海門市高二期末統考的附加題最后一題.

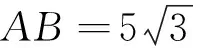
(1)求p的值；

(2)設拋物線C的焦點為F,準線為l,點A1,B1在l上,且AA1⊥l，BB1⊥l，線段A1B1的中點為Q,當AB經過F時,求證:AQ∥B1F.

原題的解答如下:

解:(1)易知p=2．

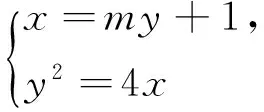
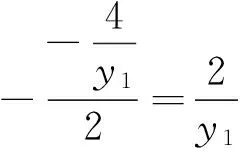
如果利用以上相關結論，可以秒殺得到BQ⊥AQ，BQ⊥B1F，從而AQ∥B1F.所以說適當的整合歸納不僅可以提高我們對學習數學的興趣,而且也可以開拓我們的視野,發展我們的思維.

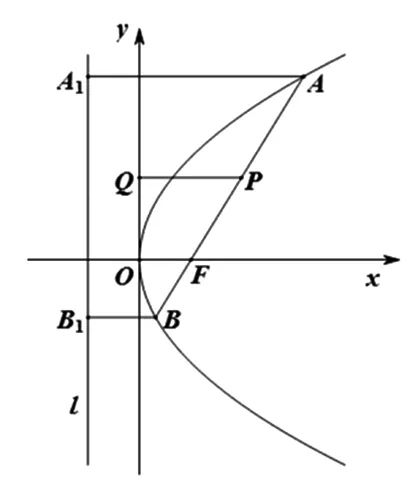
圖7

圓六(七)：若AB為y2=2px(p>0)的焦點弦，F為焦點，則以AF為直徑的圓與y軸相切(以BF為直徑的圓與y軸相切).

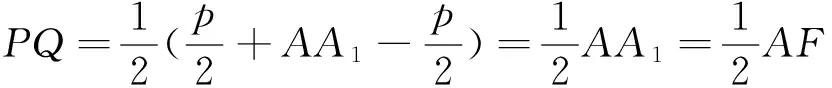
當白雪公主遇上七個小矮人，安徒生創造出了千古流傳的小故事，而當拋物線遇上了七個圓，衍生出諸多簡便的途徑，便于我們眾多考生在高考緊張的氣氛下用最快的時間抓住來之不易的分數.