歸類思維方法，為高效學習鋪路

江蘇省蘇州市張家港市合興初級中學 丁紅兵

歸類思維方法，為高效學習鋪路

江蘇省蘇州市張家港市合興初級中學 丁紅兵

初中數學知識是成體系存在的，以思維方法為依據將知識內容進行歸類，是高效開展學習的理想途徑。筆者從思維方法的角度出發，查閱了大量理論資料，并結合具體教學實例，提煉出了幾種典型性強的思維歸類方法，將之闡述于本文，望對廣大初中數學教師有所啟發。

初中；數學；思維方法

21世紀借助于互聯網，人們隨時隨地都可以從網絡獲得自己需要的知識，已經從“知識就是力量”的時代轉為“思維就是力量”的時代。教育的任務已不僅僅是培養“有知識的人”，而是更注重培養“會思維的人”、“有智慧的人”。所以筆者認為：想要學好初中數學，僅僅靠下苦功是遠遠不夠的。學習需要刻苦，更需要技巧。著眼剖析初中數學中的一個個具體知識內容，便不難發現其中存在的相似之處，繼續結合典型問題的分析與解答過程加以提煉，普適性的思維方法就出現了。從思維方法的角度進行歸類探尋，既是優質教學的高階要求，更是學生得以高效掌握數學知識的一條捷徑。

一、尋找函數方程思想，促進高效學習

函數與方程不僅是初中數學中的一個重要知識模塊，更是通行于多個知識領域的問題分析方法。站在思維方法的高度來看待函數方程，便可以為整個數學學習過程開辟一條高效的路，使之成為學生們在初中數學學習中掌握的第一種思想方法，也是必不可少的。

縱觀整個初中數學學習過程，函數方程的思維方法稱得上是適用最為廣泛的一種了。很多學生表示，當分析問題出現困難時，只要找到合適的等量關系，都可以借助函數方程的思想來予以解答。掌握這個堪稱“萬能”的思維方法，對于數學教學的高效推進來講意義重大，真可謂“函數方程是兄弟，此隱彼顯兩相依。根據需要做選擇，難題也會變容易”。

二、尋找數形結合思想，促進高效學習

“數形結合威力大，遇有難題去找它。一個問題兩側面，根據需要來轉化。”在數學知識當中，“數”與“形”之間始終存在著密不可分的聯系。找到數形之間的關聯，不僅能夠讓學生們更加到位地掌握知識內容的細節與本質，更可以在分析具體問題時為大家提供行之有效的思維工具。從數與形的關系出發思考問題，就是我們將要討論的數形結合思想。

例如，當學生們完成了數軸知識的學習后，我在課堂上引入了這樣一道題目：A、B兩個點分別表示數軸上的實數a、b，這兩個點之間的距離表示為|AB|。當兩個點當中有一個點位于原點上時，設點A位于原點，如圖1所示，|AB|=|OB|=|b|=|a-b|。當兩個點都不在原點上時，存在三種情況：當兩點均在原點左側時，如圖2所示，|AB|=|OB|-|OA|=|b|-|a|=（-b）-（-a）=|a-b|；當兩點均在原點右側時，如圖3所示，|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|；當兩點分別位于原點兩側時，如圖4所示，|AB|=|OB|+|OA|=|b|+|a|=（-b）+a=|a-b|。那么，（1）數軸上表示2和5的兩個點、表示-2和-5的兩個點、表示1和-3的兩個點之間的距離分別是多少？（2）數軸上表示x和-1的兩個點之間的距離是多少？若兩個點分別為點A和點B，且|AB|=2，則x的值是多少？（3）若要使得|x+1|+|x-2|的值取得最小，則x的取值范圍是什么？這個問題從數軸的基本問題出發進行了拓展延伸，雖然內容的難度比教材中的基礎知識增大了，但卻在圖形的引導下，十分清晰地呈現在了學生面前。借助圖形方式思考數軸問題的方法，也對學生們形成了啟發。

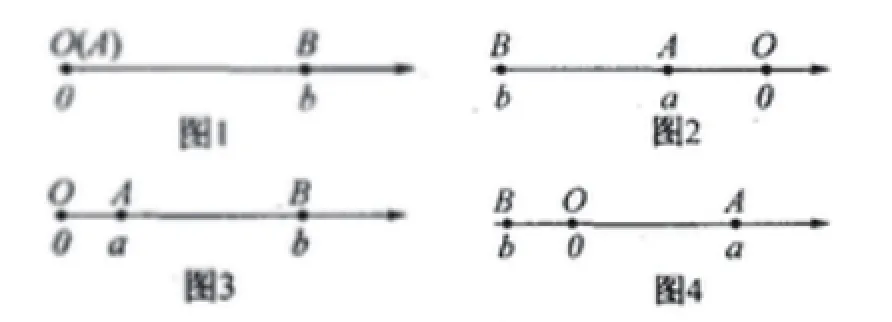
數形結合思想在初中數學教學中的適用可以從兩個角度展開：一是從問題當中已經給出的圖形入手，從中盡可能多地將已知條件挖掘出來，使圖形當中所蘊含的信息服務于數量關系的探究。二是從新圖形的構造入手，善于在閱讀當前的數量關系條件之后，以圖形的方式將之加以體現，最終實現數與形的有機整合。

三、尋找分類討論思想，促進高效學習

在一些關系比較復雜的數學問題當中，經常會出現多個思維拐點。如果學生們不能將每一種情況都考慮周全，便會造成問題解答錯誤的出現。這就對學生們的分類討論能力提出了要求。

例如，在對直角三角形的內容進行教學時，我請學生們思考這樣一道習題：正方形ABCD的邊長是10厘米，一個動點P從點A處出發，以逆時針的方向沿著正方形的邊勻速運動，運動速度為每秒2厘米，直至回到點A處時停止運動。那么，當點P運動了t秒時，它和點D之間的距離是多少？這個問題看似簡單，可真正分析起來便會發現，點D和點P存在著多種位置關系。為此，我先請學生們根據已知條件將圖形畫出（如右圖所示），然后根據點P位于正方形不同的邊上來分別分析其中的數量關系。由此，學生們意識到，應當根據0≤t＜5、5≤t＜10、10≤t＜15、15≤t≤20這四種情況進行分類討論。果然，這樣的分類一出，解題的思路立刻清晰起來了。從這個分析過程中，學生們也深切地感受到，對于情況復雜的問題，分類討論是十分必要的。明確了分類標準，并將每一種可能性都準確列出之后，解答題目的過程自然順暢高效。這樣的嘗試也讓很多對分類討論心存畏懼的學生們，找到了有效分析問題的入手點。

分類討論思想的培養，并不是靠簡單的死記硬背就能實現的，而是要以學生們對知識內容的到位理解與清晰有序的數學思維作為保障。教師們在教學過程當中，更要著重對分類的依據與方法向學生們加以強調。建立起分類討論的思維習慣之后，疑難復雜問題便能夠應對自如了。

四、尋找整體轉化思想，促進高效學習

在初中數學學習過程當中，還有一種重要的思維方法很容易被學生們所忽略，那就是整體轉化思想。這種思維方法經常會被運用在一些比較細小的解題細節當中，雖然不像前面幾種方法那樣引人注目，但適用得當，卻能夠顯著提升知識學習效率。

例如，在反比例函數內容的學習過程當中，學生們遇到了這樣一個問題：如下圖所示，點A和點C分別是直線與x、y軸的交點，點P也在這條直線上，且位于第一象限。PB與x軸垂直，垂足是點B，△ABP的面積是9。（1）點P的坐標是什么？（2）若點R與點P均在同一個反比例函數的圖象上，且點R位于直線PB的右側，作RT⊥x軸于點T，要使得△BRT與△AOC相似，則點R的坐標應當是什么？不難發現，確定點P的坐標是解答這個問題的關鍵所在。那么，怎樣明確求點P坐標應當借助的條件呢？這就需要一個順暢的思維轉化了：想要求點P的坐標，就要先求出PB和OB的長度。在具體計算的過程中，則需要將點P（m,n）的坐標轉化為方程或方程組來求解。經過從這兩個角度分別進行轉化之后，學生們求解問題的思路一下子清晰了不少。這個過程也讓大家意識到，面對一個數學問題時，不要急于下筆計算，而是要將分析問題的思路設計好，特別是如何運用已知條件加以轉化，有了這個大方向，才能高效準確地解題。

通過解答一些比較典型的數學題目，尋找整體轉化思想并不困難。鑒于它經常容易被學生們所忽略，教師們要做的就是在日常教學過程中經常性地引入這種思維方式，讓它成為學生們的一種思考習慣，使之于無形當中推動整個學習過程走向高效。

初中數學當中的知識內容數量繁多，串連它們的思維方法自然也不在少數。當學生們將這些規律性的思維方法一個個探索發現后，就好像是在手中握住了一條條繩索，逐漸將散落的數學知識串連起來了。從思維方法的角度把握數學，便可以提綱挈領地處理學習過程，從根本上推動數學學習的高效開展。

[1]李亞君.淺談初中數學的創新教學[J].學周刊，2014（14）.

[2]黃廣澤.提高初中數學教學質量的幾點認識[J].基礎教育研究，2010（11）.

[3]蓋群.巧用“做數學”,創新初中數學教學[J].中國校外教育，2014（13）.