封閉人群生存人數整體預測

王志剛　王曉軍　張學斌

摘要：由不同組別人群組成封閉人群整體生存人數的預測是相關經濟、社會問題研究的基礎。現有文獻在研究相關問題時，使用的方法為：首先根據動態死亡率模型對其中具有相同特征不同部分的生存人數進行預測，之后通過加總得到整體人數的預測（簡稱現有方法）。由于現有方法忽略了不同特征人群死亡率變動間相關性的影響，會低估生存人數的波動性。本文使用Lee-Carter模型，在將封閉人群按性別分組的基礎上，給出了構建生存人數整體預測模型的過程和實例。并通過理論分析和數值模擬兩個視角對現有方法和新方法做了比較。比較結果指出：在死亡率波動具有廣泛相關性的現實世界中，只有在均值預測時，現有方法才可以達到預期效果，因此筆者建議在對整體人數（特別是涉及方差和分布函數）預測時，使用本文介紹的整體生存人數預測模型。

關鍵詞：生存人數：Lee-Caner模型：整體預測

中圖分類號：C921

文獻標識碼：A文章編號：1000-4149（2016）04-0010-11

DoI：10.3969/j.issn.1000-4149.2016.04.002

一、引言

對于不考慮人口流動的封閉人群生存人數預測是相關經濟、社會問題研究的基礎。封閉群體人數的變動主要來自于死亡所引發的成員退出。封閉人群通常是由不同特征（例如不同性別、不同地域）人群構成。在對封閉人群生存人數進行預測時，現有文獻中主要根據某一特征對人群進行分組，在對每一組生存人數預測的基礎上，通過加總得到整體人數的預測。簡單加總的前提條件是不同特征人群死亡率變動間不具有相關性。而實際經驗和數據都顯示，不同特征人群死亡率變動是具有相關性的。簡單地忽略人群死亡率變動間相關性的影響，雖然在對生存人數期望研究時可以得到比較滿意的效果，但對方差、特定分位數和分布函數的預測就變得不再適合了。而隨著社會問題研究的深入，一些領域（例如保險精算）的研究不僅需要獲得生存人數的期望值，還需要獲得生存人數波動方差和分布函數。在現有研究方法無法滿足對方差、分位數和分布函數度量的情況下，本文將以動態死亡率模型為基礎，將不同組別問相關性納入到模型中，建立新的生存人數預測模型，以滿足實際問題研究的需要。

建立一個整體生存人數預測模型，需要完成兩方面的工作：一是將影響人口變動的死亡率模型由一維擴展為多維；在由一維擴展到多維時，就必須考慮不同組別間死亡率變動時體現出的相關性，因此第二項工作就是在分組的基礎上，準確度量不同組間死亡率變動的相關性，并將相關性研究結果納入到前面建立的多維死亡率模型中。

由于一組人群可以按不同指標分為不同組，作為整體生存人數預測實例，本文按照性別將相同年齡人群分為兩組。在展開具體問題研究時，與前面提及的邏輯順序不同，本文首先對不同性別死亡率變動過程中表現出的相關性進行深入研究：然后，將得到的相關性度量結果納入多維Lee-Carter動態死亡率模型中，進而得到按性別分組的整體生存人數預測模型；最后對現有研究方法和本文方法的預測結果進行對比研究。

二、男性和女性死亡率的相關性

剔除了人口再生產引發的成員增加和人口遷移引發的成員數的變動，此時封閉人群生存人數變動主要來自成員由于死亡而引發的退出。本節將對引發成員退出的（男性和女性）死亡率變動過程中體現出的相關性進行研究。為了后面陳述方便，先對需要使用的符號、數據和死亡率模型進行簡要的

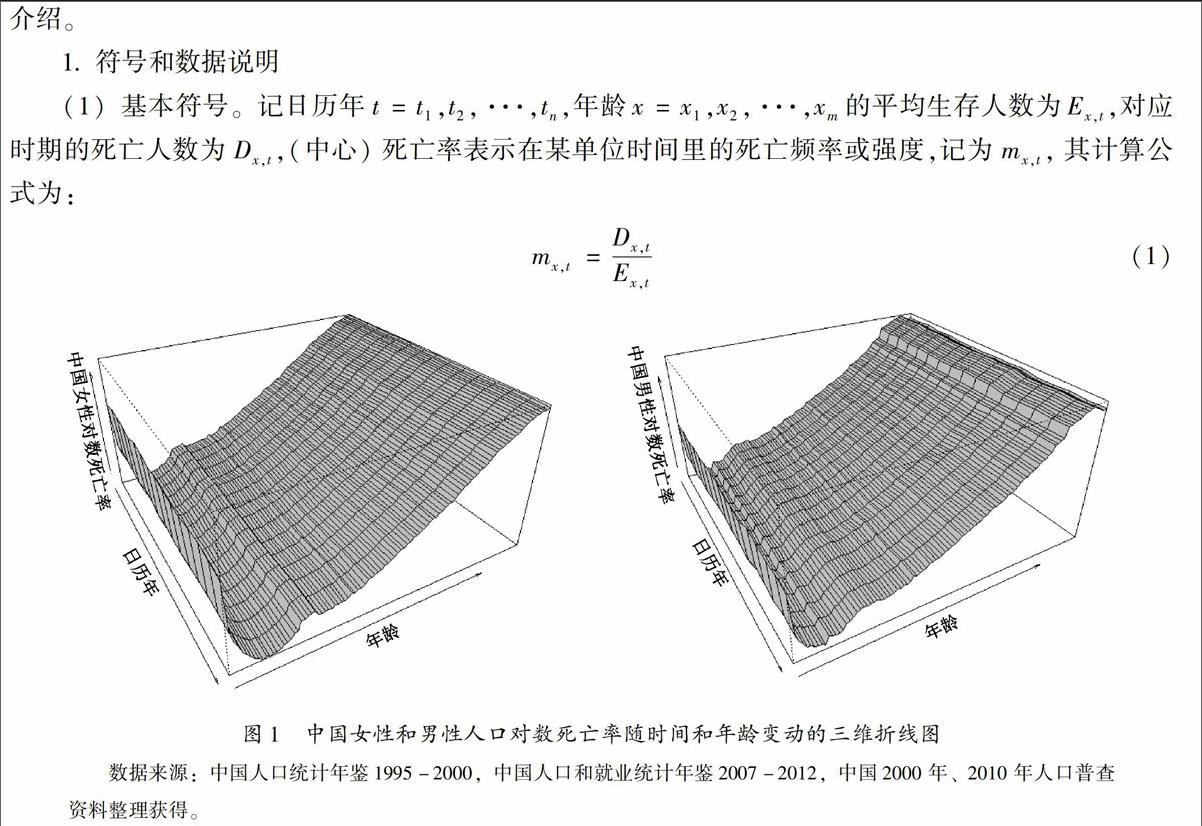
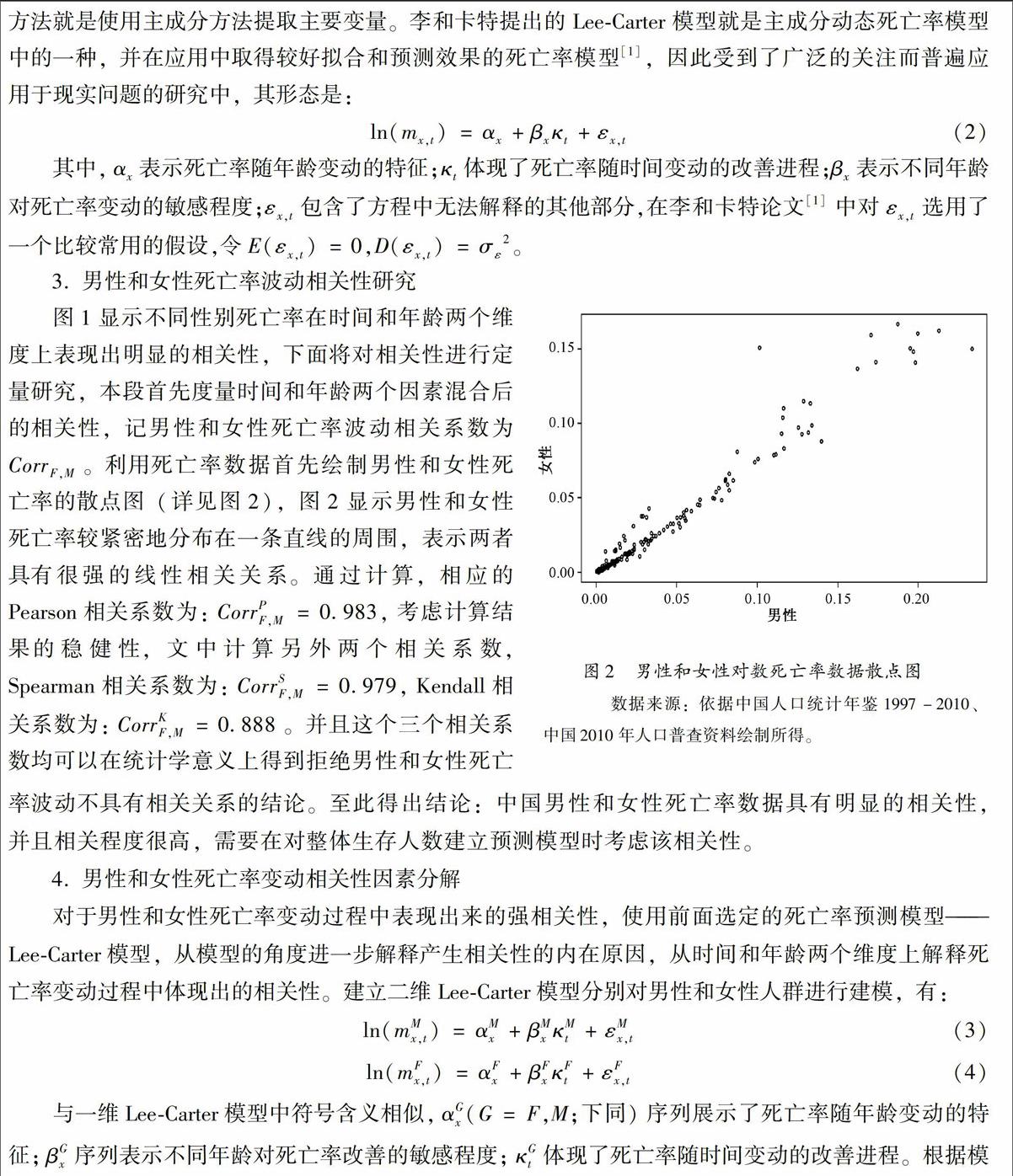
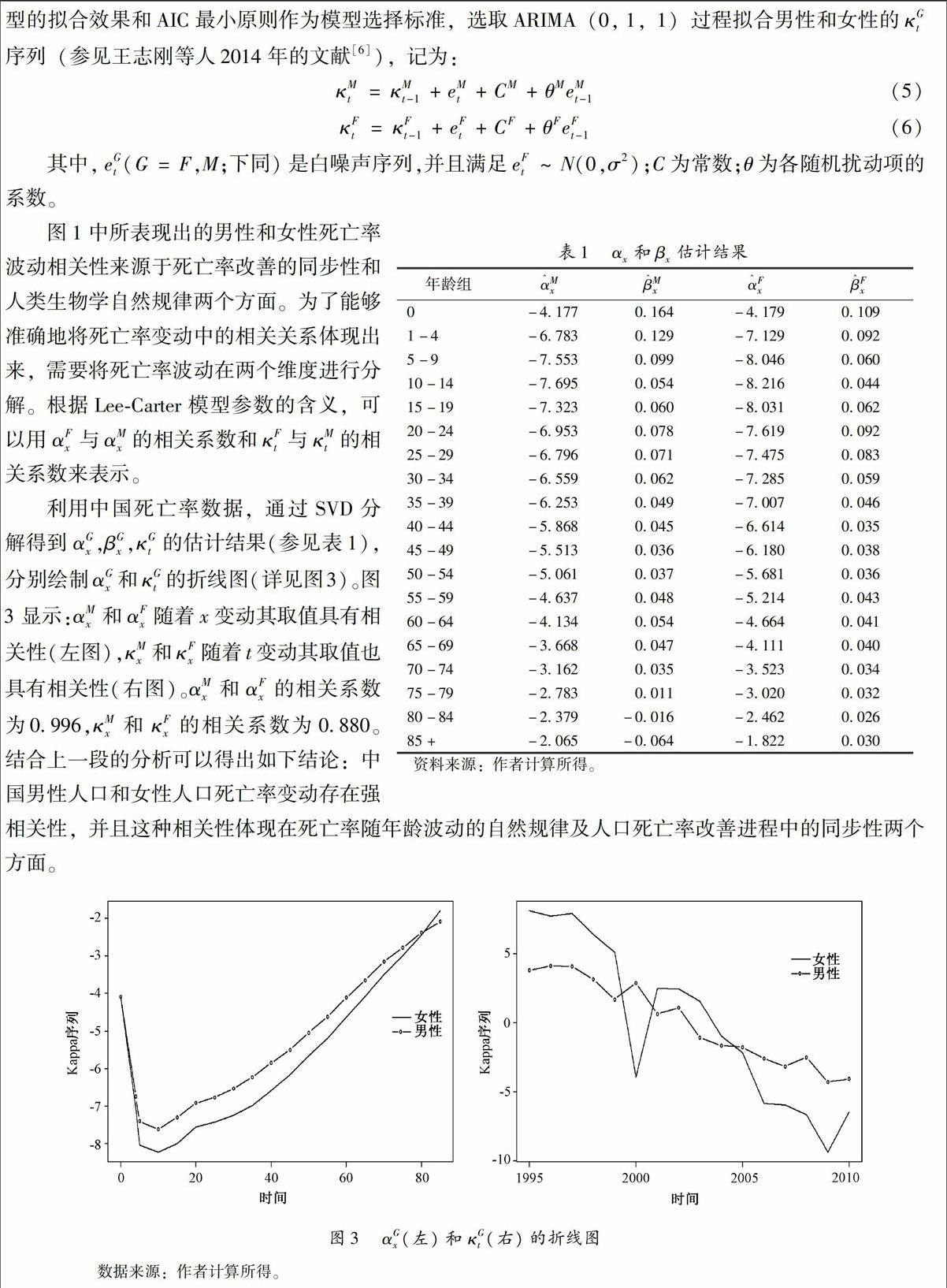
（2）數據。本文建模使用的數據來源于國家統計局公布的1995-2006年《中國人口統計年鑒》、2007-2012年《中國人口和就業統計年鑒》和2010年人口普查數據中的全國分年齡、分性別死亡人口狀況表，進而根據式（1）計算得到1995-2012年各年度分年齡（0-85歲五歲一組）、分性別的中心死亡率。為了更清晰地描述這些數據，圖1給出了我國1995-2012年連續16年0-85歲的男性和女性對數死亡率的三維圖。圖1顯示中國男性和女性對數死亡率變動具有很強的相似性，這種相似性體現了內在相近的生理特征和共同的社會、醫療水平對男性和女性死亡率改善的內在規律，這提示我們在建立整體生存人數估計時應該考慮相關性的影響。

2.動態死亡率預測模型

在將男性和女性死亡率波動過程中的相關性納入死亡率模型之前，首先需要選取一個合適的死亡率模型。常用的死亡率模型可以分為靜態和動態死亡率模型兩種，由于靜態死亡率模型不包含時間項所以無法用于預測，因此為了能夠對未來的生存人數進行預測，需要使用動態死亡率模型。

近30年來，動態死亡率模型在理論上取得了豐富的研究成果，其中包括：李（Lee）和卡特（Carter）1992年提出的Lee-Carter模型，倫肖（Renshaw）和哈伯曼（Haberman）2006年提出的Lee-Caner改進模型——RH模型，以及凱恩斯（Cairns）等人2006年提出的CBD模型。王曉軍、黃順林匯總介紹了包括以上模型在內的8個動態死亡率模型。王志剛指出一個較為理想的形態應該包含年齡項、時間和年齡交互影響項，以及出生年因素項。為了減少待估參數，一個較好的

動態死亡率模型中雖然沒有將社會、醫療等變量直接納入到模型中，但死亡率的變動綜合體現了這些因素對死亡率的影響，因此模型中的三組參數（α_x，β_x，K_t）估計結果體現了多種因素對不同年份、年齡人群的影響合力。間接體現了社會、醫療等因素變動的影響，并且在實際問題中取得了較好的擬合效果，其參數含義清晰。因此，動態死亡率模型受到了廣泛關注，其中Lee-Carter模型就被聯合國人口署和美國人口普查局等眾多機構使用，后面就以Lee-Carter模型為例，建立能夠反映男性和女性死亡率變動相關性的封閉人群生存人數整體預測模型。

三、建立生存人數預測模型

1.建立男性和女性整體死亡率預測模型

李和卡特提出的一維Lee-Carter模型最早用于美國男性人口死亡率建模，之后學者在引用該方法時，也都只限于對某一組別人群進行研究。國內研究也體現出相同特點。本文需要使用二維Lee-Carter模型對男性和女性生存人數進行整體建模，這就需要對前面選取的一維Lee-Carter模型進行擴展，建立一個能夠體現死亡率變動內在相關性的死亡率聯合模型，以使模型能夠更好體現中國男性人口和女性人口死亡率隨年齡波動的自然規律及人口死亡率改善進程中的同步性。

根據二維Lee-Carter模型中參數含義可知，式（3）和（4）中的α_xG項取值序列已經體現了死亡率隨年齡變動的規律和相關性，此時直接在模型中使用估計值便可以滿足要求，不需要在模型中再引入新的約束。

建立新舊兩種方法的預測模型后，作為實例，下面以社會養老保障和（養老）保險公司關注的老年群體為例，假設2012年初始年齡為60歲的男性和女性各10000人為例，使用前面給出的整體生存人數預測方法，對未來45年生存人數進行預測，并建立分布函數，計算均值、標準差和分位數。

（1）均值估計比較。圖4中分別繪制了使用分性別估計和整體估計得到的未來45年內男性、女性和總體生存人數均值預測值（共計6個預測值）。但在圖4中，只能清晰辨別出三條曲線，這是因為使用兩種不同方法分別得到三個期望的估計值完全一致，所以其繪制出的曲線黏合在一起，無法清晰辨別。其中（由下向上第一、二）兩（實際是四條線）條曲線，分別體現了兩種方法估計得到的男性和女性期望的預測結果，由于相關性對不同組別生存人數的估計是不產生影響的，所以兩個估計結果一致是情理之中的。另一條曲線描述了整體生存人數的期望值，由于相關性對于期望求和不產生影響，所以兩個計算結果也是一樣的，圖形上也顯示為兩條曲線黏合在一起（由下向上第三條線）。

（2）標準差和分布函數估計結果比較。對于期望估計結果，兩種方法完全一致的效果，可能會讓使用者誤認為原有方法是有效的工具（但事實上這只是一個巧合，而不是正確的路徑）。在需要生存人數的方差等相關數值時，現有的方法就沒有這樣幸運了。圖5中依然分別繪制了使用分性別估計和整體估計得到未來45年內男性、女性和總體生存人數方差的估計值（共計6個估計值）。但在圖5中，能夠清晰辨別出四條曲線，比圖4中多一條可以辨識的曲線。

圖5中（由下向上第一、二）兩條曲線，分別體現了兩種方法估計得到的男性和女性方差的預測結果（共計4條線）。由于相關性對單個組別的估計并不產生影響，所以使用兩種不同方法得到男性和女性生存人數預測值的波動方差相同，據此繪制出的四條曲線黏合在一起，只能清晰辨別出兩條。另外的兩條曲線就體現了使用兩種不同方法對整體方差估計結果的不同，其中使用獨立估計得到的男性和女性方差估計結果之和（由下向上第三條線）明顯低于對整體生存人數進行預測得到的方差值（由下向上第四條線），體現了分別估計方法對方差可能產生低估的負面影響。

標準差的不同也會引發兩種方法對生存人數分布函數的預測結果的不同，在獨立假設下較小的標準差意味著生存人數預測結果更加集中，體型更加“輕盈”；相對應的，整體生存人數預測模型的標準差較大，得到的分布函數則會更加“豐滿”（詳見圖6）。

依據模擬得到的結果還可以進一步估計該組人群的余壽，計算結果參見表3。估計結果顯示：兩種情形假設下余壽估計值是相同的，但是現有方法對于余壽波動方差的估計是明顯低于考慮相關情形下的估計結果。在兩種不同假設下，表3中給出的余壽90%置信區間分別為（14.28，15.36）和（14.05，15.54），現有方法得到的估計區間更窄，區間上限和下限差為1.18歲，而在考慮相關情形下得到的區間寬度為1.49歲，比現有方法高0.41歲。可見，現有的方法低估了余壽的波動范圍。

五、結論

通過上述分析可以得到以下結論，現有方法和本文介紹的建模方法內含了兩種不同的假設條件，本文介紹的整體生存人數預測方法更符合實際情況。雖然以Lee-Carter為代表的動態死亡率模型并沒有明確包含人口生理特征和社會、醫療條件等因素項，但體現了這些因素對死亡率變動的綜合影響。現有方法中在分別對男性和女性死亡率波動進行建模，并進而通過加總得到男性和女性生存人數之和的預測值時，對男性和女性死亡率分別獨立建模，隱含假設這些因素是分別獨立作用于男性和女性的。而現實生活中，由于內在相近的生理特征和社會、醫療等條件發生的改變同時影響男性和女性人群，使得男性和女性人群死亡率波動具有內在的關聯性，因此，在進行整體生存人數建模時，假設生理特征和社會、醫療條件對男性和女性死亡率影響具有相關性，更加符合實際。本文介紹的方法能夠很好地將這種相關性納入到模型中，所以使用整體的生存人數模型進行建模將更接近實際情況。

同時理論和數值計算結果顯示：本文給出的方法能夠更加有效地估計整體生存人數的期望、方差和分布函數。人口估計的期望值，可以理解為在未來社會和醫療條件中性變動條件下預測生存人數。此時現有方法和本文介紹的方法將基于相同的假設條件下進行計算，所以得到的結果是一致的，但這種一致應該理解為一種巧合性的一致，不能代表現有的方法是正確的。標準差體現了死亡率改善中受到社會和醫療等因素的影響，而引發的生存人數的平均波動。分別對男性和女性死亡率波動進行建模，就意味著假設這些因素是分別作用于男性和女性。這就有可能獲得假設男性人口發生死亡率改善而女性死亡率惡化的模擬結果，或是男性人口發生死亡率惡化而女性死亡率改善的模擬結果。當將男性和女性人口加總獲得整體人口研究結果時，就會對沖掉生存人數的波動，使得整體波動偏差變小，從而低估風險。本文給出的研究框架，有效地納入了死亡率變動中體現的相關性，能夠更加準確地預測生存人數的變動幅度和分布函數。

本文以性別分組為例，給出了利用動態死亡率模型構建生存人數整體預測路徑和實例，該框架也可以適用于其他二維分組和多維情況。死亡率變動體現的相關性不僅體現在一個地區內的不同組別的人群上。根據HMD（世界人口死亡率）數據庫中的數據顯示，不同地區的人群死亡率也具有很強的相關性，因此在對整體人群生存人數進行預測時，不同地域、組別人群間具有的相關性是必須應該考慮的問題，在研究這些問題時，可以參考本文的研究框架構建相應的整體生存人數預測模型。

由于經典的Lee-Carter模型被世界上多個政府、金融機構作為死亡率預測模型，本文以Lee-Carter模型為例給出的生存人數整體預測模型，有助于和國外現有相關研究成果銜接。但本文所討論的研究思路并不局限于該模型，可以擴展到其他動態死亡率模型中，以建立相應的生存人數整體預測模型。