隔膜泵用磁致伸縮致動器的設計與實驗研究

芮驥才,謝榮建,王仕越,張 添,董德平

(1.中國科學院上海技術物理研究所,上海200083;2.中國科學院大學,北京100039)

0 引 言

以磁晶各向異性補償合金TbxDy1-xFe2為代表的超磁致伸縮材料(以下簡稱GMM)在交變磁場中可發生周期性的應變,實現電磁能-機械能的轉換,GMM在室溫下的飽和應變值可高達1 500～2 000 ppm,同時具有響應速度快(μs級別)、能量密度高、輸出力大等特點,因此在微型動作元件以及流體機械中有著極強的應用優勢[1-2]。

磁致伸縮致動器是通過給GMM施加合適的交變磁場使其產生預期的位移或力的輸出的機構,本文介紹的致動器以隔膜泵作為負載,通過導桿將材料的振動傳遞至金屬隔膜從而實現驅動,設計時考慮軛鐵材料的真實物性,對整個致動器進行了有限元仿真,比較不同結構參數下的磁場分布,以形狀因數作判據選取最優值,從而實現較高的驅動效率。

1 超磁致伸縮致動器的理論分析

1.1 超磁致伸縮材料工作特性

超磁致材料的工作特性由磁致伸縮方程式(1)、式(2)表示,其應變由應力場、磁場與溫度場的共同作用引起[3]:

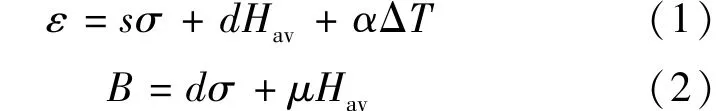
式中:ε為材料的應變;s為超磁致伸縮材料的柔順系數;σ為內部應力;d為磁致伸縮應變系數;Hav為平均磁場強度;α為熱膨脹系數;ΔT為材料的平均溫度變化;B為磁感應強度;μ為材料的磁導率。

典型的磁致應變如圖1所示。偏置壓力與磁場強度對材料的變形量影響很大,合適的偏置壓力會讓材料有更大的應變,機電耦合系數更高。同時無論磁場方向正負,磁致應變均為正值,直接導致材料工作在交變磁場中會產生“倍頻現象”,通常加入偏置磁體或直接由線圈提供偏置磁場使材料工作于線性工作區,從而避免該現象發生。

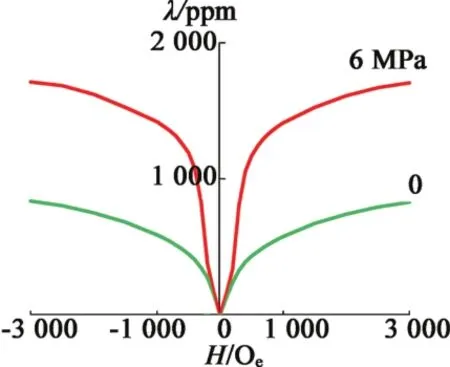
圖1 不同壓力偏置下磁致伸縮曲線

1.2 磁致伸縮隔膜泵

隔膜泵屬于容積式泵,通過活塞或者隔膜的往復運動引起泵腔內部容積變化同時配合單向閥門完成流體的吸入與排出。與常規的旋轉動力泵的不同在于,其流量輸出相對比較穩定,同時在壓縮比較大的情況下具有較強的自吸能力與抗氣泡能力[4-6]。

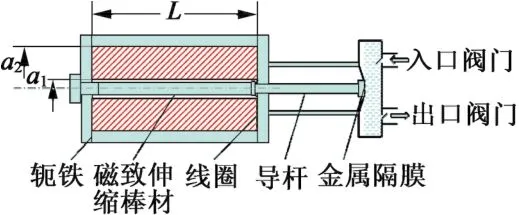
圖2 磁致伸縮隔膜泵結構示意圖

本文介紹的磁致伸縮膈膜泵工作于流體傳熱回路,通過泵送低溫流體工質通過換熱器來冷卻高溫部件,其結構簡圖如圖2所示。線圈內部通交流電產生交變磁場,超磁致材料棒在磁場中產生周期形變,通過導桿推動金屬隔膜往復運動完成吸入和排出沖程,進出口均植入單向閥門確保流動方向一致。泵體設計頻率為50 Hz,設計流量為1.8 mL/s,需要超磁致材料提供0.1 mm以上的峰峰值位移輸出,同時導桿結構在傳遞位移的同時起到減少漏熱的作用。

1.3 致動器磁路結構設計

由圖2的結構可以看出,對于提供驅動磁場的線圈來講,其主要參數為內半徑a1,外半徑a2,以及長度L,設計思路是在不超過一定的外徑時,存在一個最優的參數搭配使GMM棒材磁場達到80 kA/m時系統的發熱量最低。為描述該線圈的效率定義形狀因數

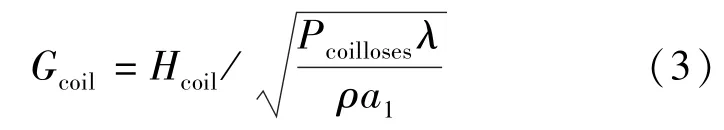
同時對于均勻密繞的線圈,其銅損:

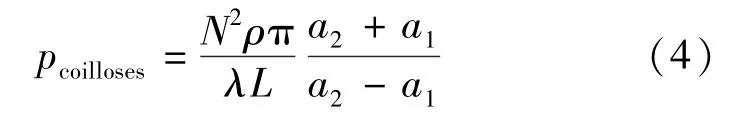
因此:

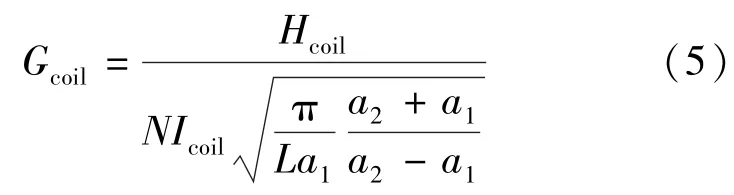
式中:Hcoil為線圈軸線中心磁場強度;λ為導線的填充因數,對于圓形截面的密繞導線一般取值π/4;pcoilloses為線圈銅損;ρ為導線電阻率;N為線圈匝數;Icoil為線圈內電流。

根據式(5)可知,在相同的安匝數NIcoil輸入下,最優的線圈應該具有最大的磁場強度Hcoil。對于帶軛鐵的致動器,其磁力線分布與在空氣中區別很大,而且由于材料磁導率的非線性,其中心場強Hcoil并不具有解析解,因此采用有限元軟件MAXWELL對整個致動器進行建模,并通過參數化分析來尋找幾何結構的最優值。

2 有限元分析

致動器的主要組成部分均為軸對稱回轉體,考慮到磁致應變上限約為總長度1‰,該形變量相對于其余部件尺寸來講非常小,因此將整個致動器視為靜態,求解器設置為軸對稱穩態問題,采用二維柱坐標系建模,超磁致棒材與兩端頂頭以及外圍軛鐵構成封閉磁路包圍線圈,磁軛材料均為電工純鐵,牌號為DT4E。系統關鍵參數如表1所示。

表1 系統關鍵參數

超磁致棒材的形狀是固定的,線圈的內徑和長度必須不小于棒材,其3個形狀參數(a1,δ,h)取值與步長見表1,邊界條件設置為氣球邊界,非結構網格的最小長度設置為0.2 mm,網格劃分如圖3所示。

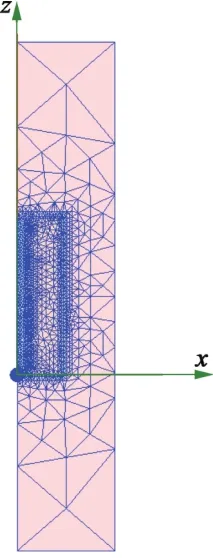
圖3 致動器網格劃分

對于每一組參數均求解出收斂后的磁場分布,圖4為a1,δ分別為8 mm和25 mm時的磁場分布。由圖4可見,僅僅在軛鐵接觸處和拐角邊界,磁感應強度的值達到最大值,接近1 T,低于電工純鐵的飽和磁密度,在磁路外部分B值較小,即軛鐵起到了很好的磁屏蔽作用;同時封閉的軛鐵磁路結構使磁力線聚攏到棒材內部,有利于在其中產生更強的磁場。取棒材中心磁場強度為Hcoil,代入到式(5)中計算當前的形狀因數Gcoil,并且作出云圖,自變量分別為a1,δ,如圖5所示。在一定范圍內形狀因數Gcoil

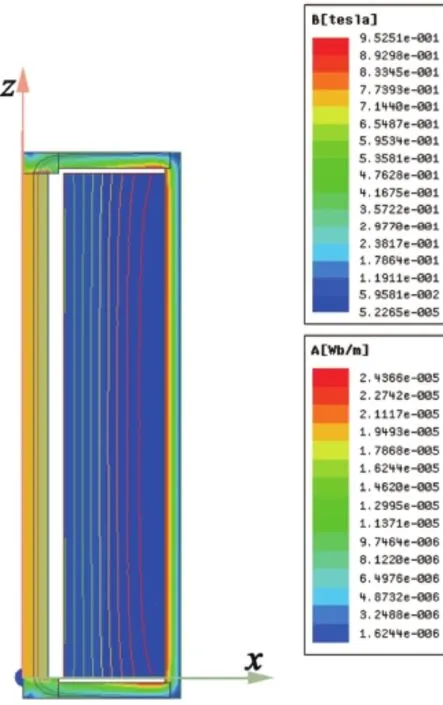
圖4 a1=8 mm,δ=25 mm時內徑磁力線和磁通密度分布

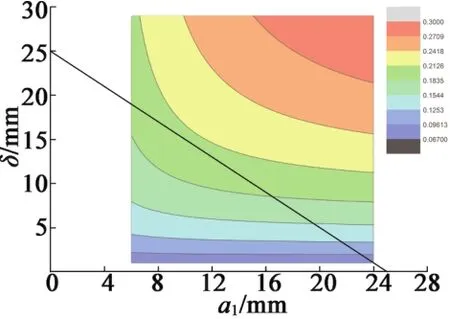
圖5 形狀因數Gcoil隨a1,δ變化云圖

隨著a1和δ的增大而增大,并且存在最優點,但要達到這個最優點,致動器的外徑會非常大,考慮實驗環境接口以及致動器重量的限制,將線圈外徑限定在50 mm以內,即在本致動器的設計中線圈外半徑不可超過25 mm,即有如下關系式:

該限定區域在圖5中為直線以下部分,提取原始數據得到a1和δ滿足要求的最優取值組合:

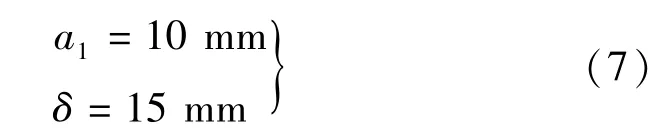
磁場的均勻性可以通過增加補償線圈或者改變軛鐵的形狀來實現。本文從后者入手,保持磁路封閉情況下,線圈越長,頂頭越長,以線圈比材料棒多出的長度h為變量,單獨進行參數化模擬并得到沿軸線場強分布如圖6所示。可見,隨著線圈超出棒材部分長度的增大,沿軸線場強的均勻度逐步惡化,不均勻度從3%發展到90%,磁場的過度不均勻會導致材料的性能變差,降低棒材的輸出力和位移,因此采用h=0時的方案,即線圈長度等于棒材長度100 mm。

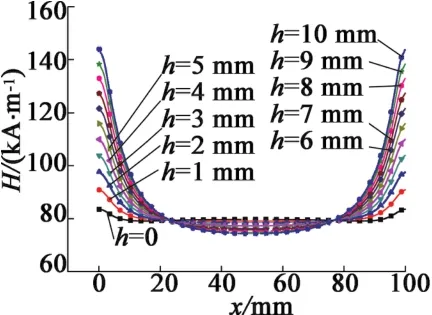
圖6 不同線圈長度下沿軸場強分布

3 實驗研究

3.1 超磁致致動器實驗研究

根據前文所述的致動器參數如表2所示。實驗測試平臺如圖7所示,考慮棒材需要在合適的壓應力偏置下工作,通過預緊螺釘以及植入稱重傳感器來監視棒材受力情況;變頻電壓源可以提供不同幅值的AC+DC電壓;激光位移傳感器來測量輸出頂頭的位移值;整個致動器外圍包裹水冷,將其溫度控制在25℃±2℃之內。

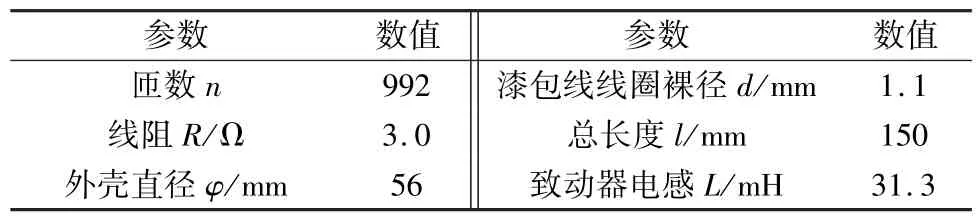
表2 致動器參數

圖7 位移測試系統

在不同預緊力情況下對致動器輸入不同直流電得到相應的變形值結果如圖8所示。磁致應變ΔS隨著電流的增加而增加,磁致伸縮系數d經歷了由大變小的過程,在電流低于4 A時應變跟電流呈較強的線性關系,并且應變系數很大,隨后趨于平緩;電流為8.5 A時達到最大應變1 100 ppm,此時偏置壓力為400～700 N,對應壓應力為5～9 MPa。

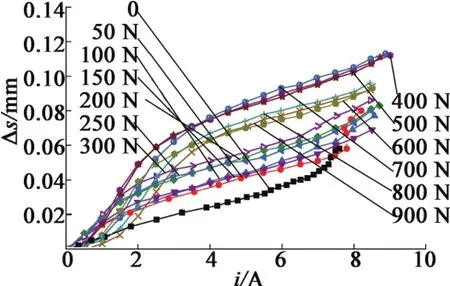
圖8 不同偏置壓力下靜態磁致應變

固定預緊力5 MPa,線圈通4 A的偏置直流電,在此基礎上疊加50 Hz不同幅值的交流電壓,得到一系列不同的位移振幅,其峰-峰值Ap-p隨電壓變化如圖9所示。隨著疊加的交流電壓幅值的增大,輸出位移近似線性增長,當電壓超過20 V,輸出位移增長幅度減小;超過25 V后交流電幅值超過直流偏置,導致輸出波形波峰變平現象,這是因為超磁致材料在H=0附近應變值非常小,反映在輸出波形上即隨著電流的變化,位移基本不變的情況。

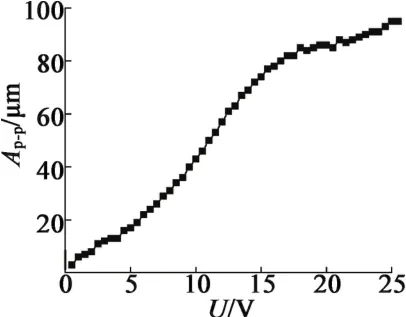
圖9 4 A直流偏置時位移-電壓曲線

保持直流偏置電壓不變,交流電壓固定為25 V,頻率從10 Hz變化至150 Hz得到致動器的位移-頻率響應曲線,如圖10所示。致動器可以看成是電阻電感串聯,隨著頻率升高,其總阻抗Z～=R+jωL的幅值|Z～|會增加,導致內部電流峰-峰值減小,另一方面,超磁致材料本身具有的“磁滯”現象也會隨著頻率的增高而逐漸使輸出位移變小。

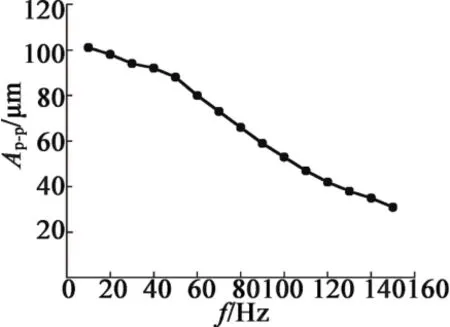
圖10 振幅峰-峰值隨頻率變化曲線

3.2 隔膜泵的實驗研究

將金屬隔膜泵體接到致動器的后端,通過導桿將振動傳遞到隔膜上,配合單向閥片來實現流體工質的單向輸運并對泵進行性能測試。實驗測試平臺如圖11所示,整個實驗在大氣環境中進行,管路中植入壓力傳感器和體積流量傳感器,通過閥門手動調節泵的背壓。

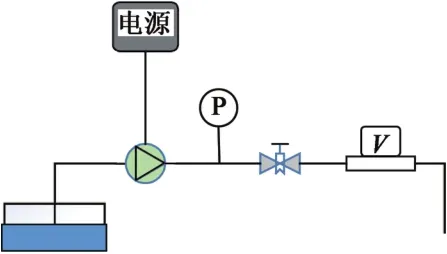
圖11 隔膜泵性能測試平臺示意圖

測試得到一系列的壓頭與流量的輸出關系曲線,如圖12所示,流動工質為乙醇。在11.8 V(DC)和25 V(AC),50Hz的電壓驅動下,金屬隔膜泵具有最大流量2 mL/s,最大壓頭接近202.650 kPa。在此基礎上固定電壓幅值,改變輸入頻率得到泵的流量-頻率曲線,如圖13所示。其中流量的理論值計算如下:

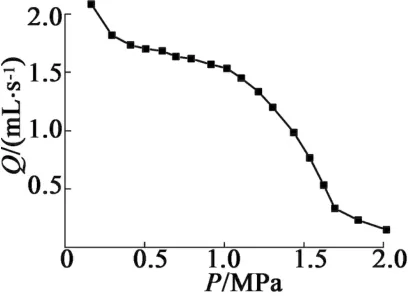
圖12 壓頭-體積流量曲線

圖13 不同頻率下的理論-實驗流量對比

實際隔膜泵工作頻率為10～100 Hz,遠小于金屬隔膜的共振基頻(模態分析結果為2 950 Hz),因此可以認為致動器對隔膜的驅動為準靜態驅動,隔膜并未發生共振,單沖程的流量即為隔膜變形的掃

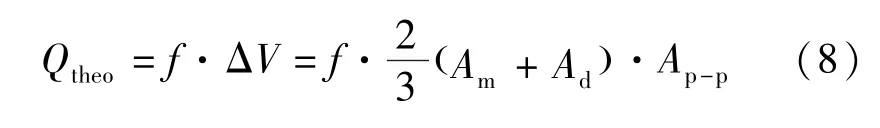
式中:f為驅動頻率;Am為隔膜面積,直徑為34 mm的圓;Ad為導桿與隔膜接觸面積,直徑12 mm;Ap-p為該頻率下致動器的最大位移輸出,具體數值如圖9所示。

由圖13可見,流量的實驗值與計算值在實際運行頻率范圍內基本吻合,均是在頻率較低時線性上升,到一定程度后基本保持不變。過圓臺體積,因此理論流量估算:

4 結 語

本文介紹了用于驅動金屬隔膜泵的超磁致伸縮致動器的磁路設計以及實驗驗證,主要包括以下內容:

基于有限元軟件MAXWELL對致動器磁路進行了仿真,通過真實結構的形狀因數來衡量磁路結構的合理性,從而得到了最優的線圈內外徑參數以及合適的長度;

對致動器的靜態與動態位移輸出進行了測試,結果為最大磁致應變達到1 100 ppm,最大振動輸出值為 100 μm;

搭載隔膜泵進行了性能測試,50 Hz下該泵具有最大2 mL/s的流量輸出,頻率變化下的流量輸出與計算值符合得一致。

參考文獻

[1] 王博文.超磁致伸縮材料制備與器件設計[M].北京:冶金工業出版社,2003.

[2] 王傳禮,丁凡,張凱軍.超磁致伸縮執行器及其在微小流體泵中的應用[J].液壓與氣動,2002(11):26-28.

[3] ANJANAPPA M,BI J.A theoretical and experimental study of magnetostrictive mini-actuators.Smart Materials and Structures[J].1994,3(2):83-91.

[4] LASER D,SANTIAGO J.A review of micropumps.Journal of micromechanics and microengineering[J].2004,14(6):37-64.

[5] RICHTER M,LINNEMANN R,WOIAS P.Robust design of gas and liquid micropumps[J].Sensors and Actuators A Physical,1998,68(1-3):480-486.

[6] LIU D H,LIU L W,TANG G,et al.A design and research on GMM precision flow pump[J].Applied Mechanics&Materials,2014(8):117-121.

[7] ENGDHL G.Handbook of giant magnetostrictive materials[M].LosAngele:Academic Press,2000,.