永磁同步電動機(jī)神經(jīng)元PID控制設(shè)計與仿真
于 淼,婁 鵬,孫 偉
(中國電子科技集團(tuán)公司第二十一研究所,上海200233)
0 引 言
對于永磁同步電動機(jī)而言,矢量控制技術(shù)的出現(xiàn)使得交流電動機(jī)的控制性能得到了質(zhì)的提升[1],矢量控制的核心是勵磁電流和轉(zhuǎn)矩電流的解耦控制,并解決了交流電機(jī)自身耦合的不足。直接轉(zhuǎn)矩控制技術(shù)也是基于磁場與轉(zhuǎn)矩分別獨(dú)立控制的思想,但采用的是比較巧妙的技術(shù)——具有繼電器特性的砰砰控制和電壓矢量查詢表[2]。
永磁同步電動機(jī)控制不僅要調(diào)節(jié)的變量多,且模型還有復(fù)雜的非線性、強(qiáng)耦合等特點(diǎn),工作情況復(fù)雜,諸多電動機(jī)參數(shù)都會發(fā)生著一定程度的變化,從而影響著交流電動機(jī)的實際控制性能[3]。隨著自動控制技術(shù)的飛速發(fā)展,一些先進(jìn)的控制方法不斷涌現(xiàn),參數(shù)辨識技術(shù)、自適應(yīng)控制技術(shù)、基于神經(jīng)網(wǎng)絡(luò)和模糊控制等先進(jìn)的控制控制算法逐步融入到電動機(jī)控制技術(shù)中,一定程度提高電機(jī)控制的快速穩(wěn)定性和魯棒性[4]。
1 永磁同步電動機(jī)轉(zhuǎn)子磁場定向矢量控制
為了建立一個可以從0°到360°可控的磁場,需要利用α-β坐標(biāo)系和d-q坐標(biāo)系,以方便系統(tǒng)模型變量解析,iABC-iαβ變換與iαβ-idq變換如圖 1 所示[5]。
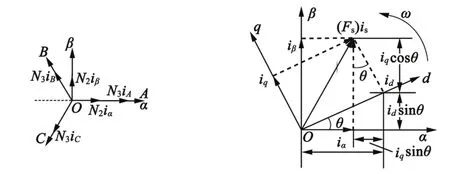
圖 1 iABC-iαβ變換與變換
電磁轉(zhuǎn)矩Te對能夠使定子和轉(zhuǎn)子產(chǎn)生相對運(yùn)動,永磁同步電動機(jī)的調(diào)速控制,即是控制電機(jī)內(nèi)部的電磁轉(zhuǎn)矩Te[6]。永磁同步電動機(jī)在dq轉(zhuǎn)子坐標(biāo)系中的轉(zhuǎn)矩公式:
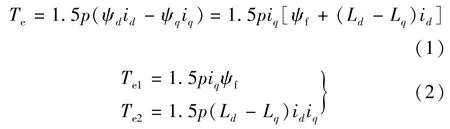
可見轉(zhuǎn)矩分量都與iq成正比,因此若要控制永磁同步電動機(jī)磁場轉(zhuǎn)矩,實現(xiàn)轉(zhuǎn)矩伺服或者速度伺服,可以通過調(diào)節(jié)定子電流轉(zhuǎn)矩分量來實現(xiàn)。
2 神經(jīng)元解耦控制
神經(jīng)元解耦算法具有在線學(xué)習(xí)整定系統(tǒng)參數(shù)、消除耦合的優(yōu)勢,成熟的神經(jīng)元解耦器不斷運(yùn)用在控制系統(tǒng)中[7]。單神經(jīng)元網(wǎng)絡(luò)可以由一個或者多個神經(jīng)元組成,X定義輸入模式的元素,T定義目標(biāo)相關(guān)聯(lián)的元素,利用單輸入神經(jīng)元樣本,求取最小偏差值y,可以用來實現(xiàn)系統(tǒng)的解耦控制問題,其對應(yīng)的解耦過程如圖2所示。

圖2 解耦過程圖
圖2對應(yīng)的解耦過程可以理解為如下的數(shù)學(xué)公式:
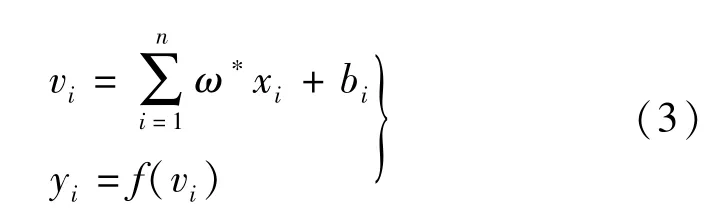
其向量形式可以表示成:

式中:xi為給定輸入信號變量;bi為神經(jīng)元i的閾值;ω是神經(jīng)元i連接權(quán)值;f(·)稱為激發(fā)函數(shù)或響應(yīng)函數(shù)。MATLAB中算法實現(xiàn)如圖3所示。

圖3 算法流程圖
永磁同步電動機(jī)的控制模型對應(yīng)輸入輸出可以表示:
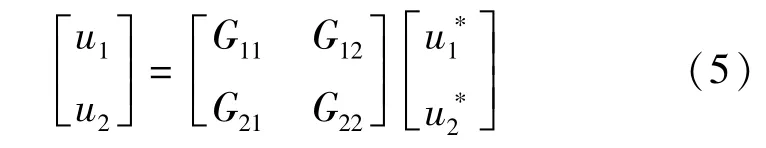
將單神經(jīng)元解耦控制器融入到永磁同步電動機(jī)控制模型后,式(5)便可以得到一個廣義對象,可以表示:
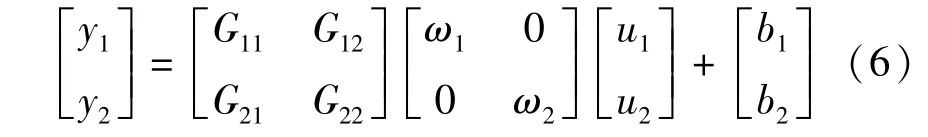
采用W-H學(xué)習(xí)規(guī)則修訂正權(quán)矢量,即采用最小均方和作為網(wǎng)絡(luò)收斂的準(zhǔn)則。神經(jīng)網(wǎng)絡(luò)的目標(biāo)訓(xùn)練公式:
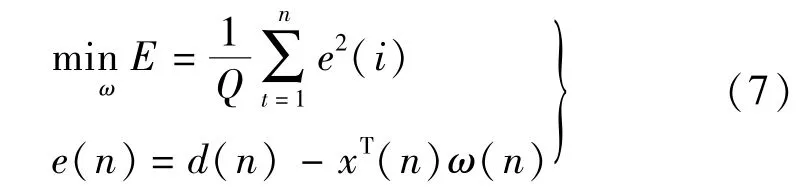
Q是給定模型的取樣數(shù)目,神經(jīng)網(wǎng)絡(luò)調(diào)整的過程是找到最優(yōu)的權(quán)值ω,使得模型誤差結(jié)果均方差達(dá)到最小。通過用對權(quán)值ω求偏導(dǎo),令該偏導(dǎo)的表達(dá)式等于零,即可求解得出的極值。
建立永磁同步電動機(jī)單神經(jīng)元解耦控制系統(tǒng)模型如圖4所示。電機(jī)控制系統(tǒng)動態(tài)結(jié)構(gòu)圖中包含兩個閉環(huán)控制,一個是轉(zhuǎn)速的外環(huán)控制,另一個是電流的內(nèi)環(huán)控制。電流調(diào)節(jié)器和轉(zhuǎn)速調(diào)節(jié)器模型的輸入端均加上PI模塊和神經(jīng)元解耦模塊,目的在于消除控制模型的系統(tǒng)誤差和變量解耦。
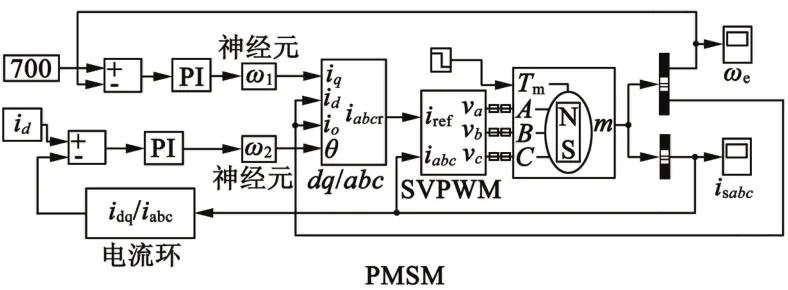
圖4 模型結(jié)構(gòu)圖
在MATLAB仿真模塊中建立單神經(jīng)元永磁同步電動機(jī)控制系統(tǒng)模型,神經(jīng)元解耦控制器外部接入多個延遲節(jié)拍,映射相應(yīng)的控制算法。針對神經(jīng)元解耦算法研究,圖4中永磁同步電動機(jī)本體模型使用仿真模型庫中現(xiàn)有的模型,這種理想的線性模型對應(yīng)的輸入輸出也存在耦合情況。
權(quán)值ω是一個在線學(xué)習(xí)且不斷整定的值,在系統(tǒng)啟動后開始自學(xué)習(xí),最終收斂,如圖5所示。系統(tǒng)誤差收斂且趨于0后,ω收斂于定值。

圖5 單神經(jīng)元解耦控制器ω調(diào)整過程
輸入速度指令并使電機(jī)運(yùn)轉(zhuǎn)在此轉(zhuǎn)速下,瞬間施加25 N·m轉(zhuǎn)矩,此時電機(jī)對應(yīng)的轉(zhuǎn)速波動波形如圖6所示。
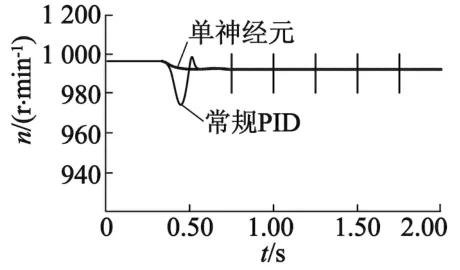
圖6 突加力矩載荷響應(yīng)曲線比對比
單神經(jīng)元解耦控制模型轉(zhuǎn)速響應(yīng)明顯比常規(guī)PID控制快,且轉(zhuǎn)速上下跳變值低。瞬間施加轉(zhuǎn)矩前,這兩類不同策略模型對應(yīng)的轉(zhuǎn)速波動為4 r/min。瞬間施加轉(zhuǎn)矩后,采用神經(jīng)元的控制模型電機(jī)轉(zhuǎn)速未出現(xiàn)明顯振蕩,受到突加轉(zhuǎn)矩的影響,轉(zhuǎn)速略微掉至996 r/min,然后在2 r/min內(nèi)波動,最后穩(wěn)定到996 r/min。采用常規(guī)PID的控制模型在突加載荷瞬間轉(zhuǎn)速掉至975 r/min,突變較大,在轉(zhuǎn)速996 r/min穩(wěn)定之前出現(xiàn)了明顯的波動。
3 PID控制器設(shè)計
PID中加大kp值能提高系統(tǒng)調(diào)整速率,同時可能會使控制系統(tǒng)振蕩現(xiàn)象加劇,調(diào)整ki值的目的在于削弱系統(tǒng)穩(wěn)態(tài)誤差,但使模型過渡時間增加,添加kd值能夠避免調(diào)節(jié)對象溢出,卻會使系統(tǒng)在一定程度上響應(yīng)速度降低。因此傳統(tǒng)的PID控制方法對于轉(zhuǎn)矩和轉(zhuǎn)速控制精度要求高的永磁同步電動機(jī)伺服控制系統(tǒng)難以滿足。在控制系統(tǒng)中發(fā)揮神經(jīng)網(wǎng)絡(luò)的在線學(xué)習(xí)優(yōu)勢,根據(jù)階躍區(qū)間信號和系統(tǒng)所能承受的“能力”來調(diào)整優(yōu)化PID參數(shù)值。本文根據(jù)電機(jī)系統(tǒng)控制特性設(shè)計一種PID控制器,在不同的控制區(qū)間整定出最優(yōu)的控制參數(shù),快且無超調(diào),使控制器的適應(yīng)性大大改善。
一般的控制系統(tǒng)都具有如圖7所示的響應(yīng)波形。按特征階段分為4個區(qū)間,可以根據(jù)圖7中的波形整定PID調(diào)節(jié)器在不同的階躍區(qū)間系數(shù)。
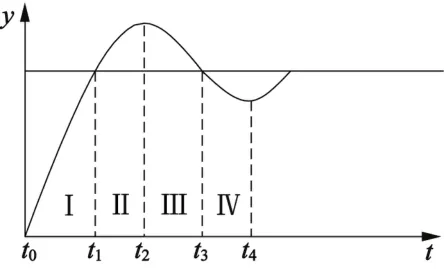
圖7 控制系統(tǒng)分區(qū)間階躍響應(yīng)波形
(1)比例增益系數(shù)kp
Ⅰ區(qū)間,控制系統(tǒng)作用初始階段,響應(yīng)速度要求快,應(yīng)增加kp值,但kp過大會引起系統(tǒng)出現(xiàn)超調(diào),因此在控制系統(tǒng)接近輸入值時適當(dāng)減小kp值。Ⅱ區(qū)間,為了加快向下調(diào)節(jié)作用,使控制系統(tǒng)調(diào)整速度加快,kp值應(yīng)緩慢增加。Ⅲ區(qū)間,降低控制系統(tǒng)輸出滯后,使控制量平穩(wěn),kp應(yīng)該緩慢降低;Ⅳ區(qū)間,kp應(yīng)緩慢加大,效果與Ⅱ區(qū)間類似。另外kp主要是加快響應(yīng)速度,獲得較小的超調(diào)量,因此可以設(shè)計kp值與e(t)絕對值成正比。根據(jù)上述整定趨勢,把kp與系統(tǒng)偏差e(t)的對應(yīng)關(guān)系描述為如下函數(shù)模型:
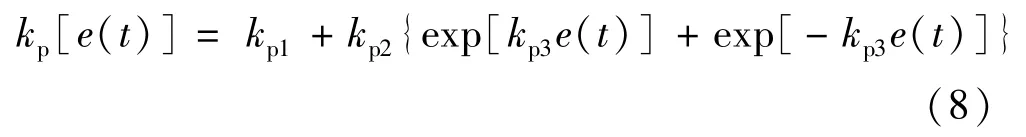
(2)積分增益系數(shù)ki
在控制系統(tǒng)誤差變大階段,減小ki值可以降低系統(tǒng)超調(diào)效果,避免控制系統(tǒng)出現(xiàn)振蕩響應(yīng)結(jié)果;在控制系統(tǒng)誤差變小后,增大ki值可以削弱穩(wěn)態(tài)誤差。因此,把ki與系統(tǒng)偏差e(t)的對應(yīng)關(guān)系描述為如下函數(shù)模型:
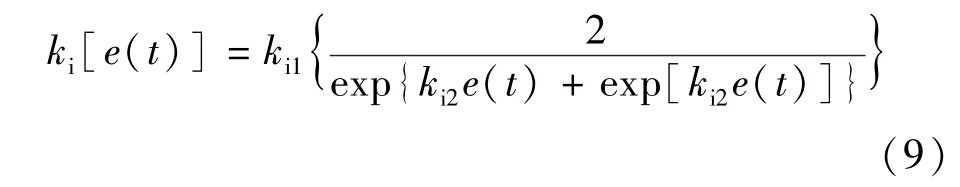
式中:ki2調(diào)整ki的變化速率。
(3)微分增益系數(shù)kd
Ⅰ區(qū)間,控制系統(tǒng)作用初始階段,給定一個較小的kd值,并使其緩慢增加,可以避免出現(xiàn)超調(diào),同時不會干擾控制系統(tǒng)響應(yīng)靈敏度;Ⅱ~Ⅳ區(qū)間,進(jìn)一步加大kd可以增強(qiáng)系統(tǒng)的向下能力,降低超調(diào)幅值。但隨著響應(yīng)延長,kd值應(yīng)該鎖定在一段區(qū)間內(nèi)。
ev(t)為偏差e(t)的變化速率,其符號需要被考慮,把kd與系統(tǒng)偏差e(t)和ev(t)的對應(yīng)關(guān)系描述為如下函數(shù)模型:
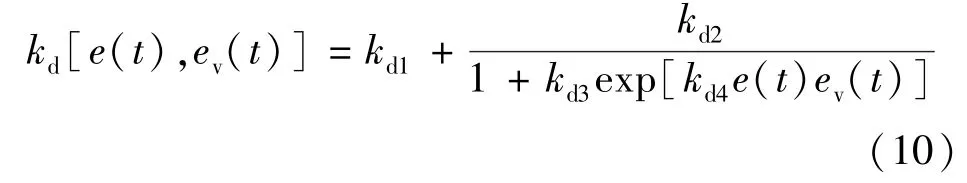
式中:kd4調(diào)整kd的變化速率。
4 仿真結(jié)果
在控制模型中給定電機(jī)載荷為30 N·m轉(zhuǎn)矩,分別使用常規(guī)的PID控制模型和本文設(shè)計的單神經(jīng)元解耦PID模型,電機(jī)起動從零轉(zhuǎn)速增加至1 000 r/min,對應(yīng)的速度曲線如圖8所示。
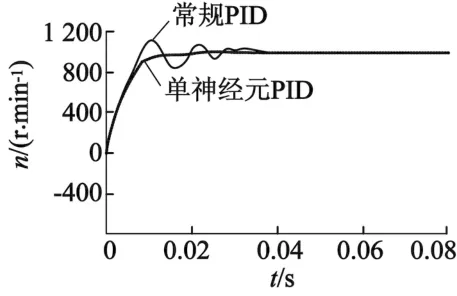
圖8 轉(zhuǎn)速波形對比
在控制模型中卸掉負(fù)載,重新起動電機(jī),在速度穩(wěn)定在998 r/min情況下,瞬間施加30 N·m負(fù)載,對應(yīng)的速度響應(yīng)曲線如圖9所示。
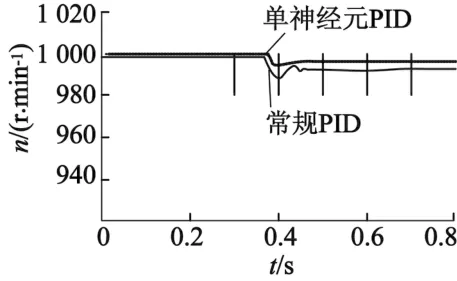
圖9 神經(jīng)元解耦與常規(guī)PID控制方式擾動響應(yīng)曲線
分析仿真結(jié)果可知,本文的神經(jīng)元PID控制雖然在一定程度上削弱了電機(jī)控制系統(tǒng)的響應(yīng)速度,但是使控制系統(tǒng)沒有超調(diào),且增強(qiáng)了電機(jī)轉(zhuǎn)速的穩(wěn)定精度。對比常規(guī)的PID控制策略,電機(jī)轉(zhuǎn)速穩(wěn)態(tài)誤差為2 r/min,轉(zhuǎn)速超調(diào)量降低為3%,但系統(tǒng)的穩(wěn)態(tài)誤差接近0,被控量沒有超出期望值,且調(diào)節(jié)過程中沒有來回波動。瞬間施加轉(zhuǎn)矩負(fù)載30 N·m時,轉(zhuǎn)速最大偏差為6 r/min,對比分析可得本文的神經(jīng)元PID使電機(jī)控制系統(tǒng)的抗干擾能力增加。
5 結(jié) 語
通過分析永磁同步電動機(jī)控制模型的被控對象與調(diào)節(jié)量,結(jié)合磁場定向矢量控制坐標(biāo)變換數(shù)學(xué)原理,在MATLAB中建立永磁同步電動機(jī)仿真控制模型。在控制模型的速度環(huán)和電流環(huán)加入單神經(jīng)元解耦器,以消除系統(tǒng)控制量與被控量相互耦合作用,根據(jù)控制系統(tǒng)分區(qū)間階躍響應(yīng)波形,設(shè)計一種PID控制器。通過仿真結(jié)果對比發(fā)現(xiàn),神經(jīng)元PID控制方法系統(tǒng)響應(yīng)速度依然較快,且對比常規(guī)PID控制方式,超調(diào)和振蕩效果被消除,且突加載荷,速度波動更小,驗證了這種模型的正確性和可行性。
參考文獻(xiàn)
[1] 秦憶.現(xiàn)代交流伺服系統(tǒng)[M].武漢:華中理工出版社,1995:37-42.
[2] 黃守道.電機(jī)瞬態(tài)過程分析的MATLAB建模與仿真[M].1版.北京:電子工業(yè)出版社.2013.
[3] 袁登科.永磁同步電動機(jī)變頻調(diào)速系統(tǒng)及其控制[M].北京:機(jī)械工業(yè)出版社,2015.
[4] 徐邦荃.直流調(diào)速系統(tǒng)與交流調(diào)速系統(tǒng)[M].武漢:華中理工大學(xué)出版社,2000:156-287.
[5] 吳利剛.基于模糊邏輯的永磁同步電機(jī)控制算法研究[D].長沙:湖南大學(xué),2012.
[6] 覃甫軍.永磁同步電機(jī)伺服控制系統(tǒng)設(shè)計與仿真驗證[D].成都:電子科技大學(xué),2012.
[7] 孫冠群,于少娟.控制電機(jī)與特種電機(jī)及其控制系統(tǒng)[M].北京:北京大學(xué)出版社,2011:147-151.

