一種外伸梁式彈簧定子超聲波電動機的設計

董迎暉,趙言安,顧雅春

(合肥工業大學,合肥230009)

0 引 言

超聲波電動機是一種利用壓電元件的逆壓電效應、彈性體超聲頻域內的諧振和定、轉子之間的摩擦傳動實現致動輸出的新型電機[1]。與傳統的電磁電機相比,超聲波電動機具有結構簡單緊湊、響應快、控制精度高、轉速低、能量密度大、無電磁干擾、無噪聲污染等優點[2-3]。目前,超聲波電動機已應用于航空航天、汽車工業、生物醫學、精密儀器等領域[4]。

毫米量級的微型彈簧定子超聲波電動機由于更為短小輕薄的結構,在微尺寸領域更具優勢。微型超聲波電動機按定子形狀可分成三類:管式定子超聲波電動機、柱式定子超聲波電動機和彈簧定子超聲波電動機。管式超聲波電動機國外研究較多,典型的有T.Morita等[5]研制的壓電薄膜管式超聲波電動機;S.X.Dong等[6]研制的管式壓電陶瓷超聲波電動機。國內方面,朱華[7]和王天華[8]等對上述幾種管式超聲波電動機進行優化改進。柱式超聲波電動機以國內研究為主,但是這種超聲波電動機采用管式定子,結構較為復雜,進一步微小化存在較大的難度。Tadashi Moriya[9]等人于2005年提出一種用Lamb波驅動的彈簧定子超聲波電動機,取一個直徑為0.3 mm的不銹鋼絲作轉子,將另一直徑為0.25 mm的不銹鋼絲繞在轉子上形成螺旋狀的定子。該電機結構簡單,尺寸微小,被應用于血管超聲波掃描儀中。但此種電機需要較長的波導,占用空間,而且輸出扭矩較小,能量損耗大,應用受限。為解決采用Lamb波驅動的彈簧定子超聲波電動機存在的問題,我們曾提出一種采用彎曲行波驅動的彈簧定子超聲波電動機,電機的結構如圖1所示[10]。將兩組壓電陶瓷粘貼在彈簧定子的兩端面上,施加電壓以激發定子的兩相彎振模態,利用模態疊加法將這兩相彎振模態合成驅動行波。由于彈簧定子兩端面是曲面,壓電陶瓷的粘接不可靠,影響電機的實際工作性能。在此基礎上,本文提出一種改進結構的外伸梁式彈簧定子超聲波電動機,用一塊外伸梁跟彈簧定子固連,將壓電陶瓷固定在外伸梁上,解決了壓電陶瓷粘接不可靠的問題。

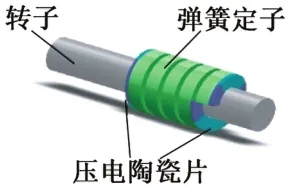
圖1 彈簧定子超聲波電動機結構示意圖

1 電機的基本結構和驅動原理

超聲波電動機的基本結構示意圖如圖2所示。定子由壓電陶瓷、外伸梁、連接板和彈簧4部分組成。轉子、彈簧定子、外伸梁與連接板的材料均為不銹鋼,其中彈簧截面為正方形;外伸梁結構通過兩片連接板焊接在彈簧左右端的螺圈上;在外伸梁的3個外表面上粘貼3片壓電陶瓷,粘貼位置如圖2所示。

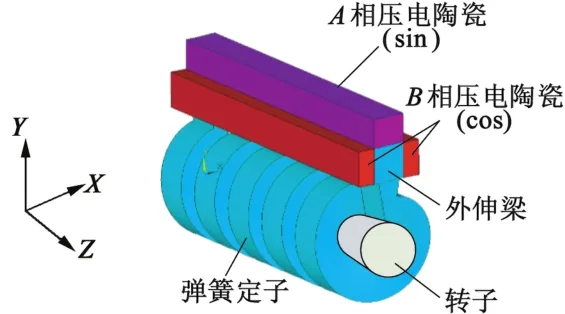
圖2 外伸梁式彈簧定子超聲波電動機結構示意圖

本文所提出的外伸梁式彈簧定子超聲波電動機采用模態疊加法產生行波,壓電陶瓷的極化方向如圖3所示。為使超聲波電動機能夠安全的使用,故將3片壓電陶瓷的內表面接地;上方壓電陶瓷沿Y軸正向極化,并在壓電陶瓷外表面施加正弦激勵電壓,以激發彈簧沿Y軸方向的一階彎曲振動;左右兩塊壓電陶瓷沿X軸正向極化,并在壓電陶瓷外表面施加余弦激勵電壓,以激發彈簧沿X軸方向的一階彎曲振動。這兩相一階彎曲振動各在時間上相差π/2相位、空間上相互垂直,由模態疊加可知,當這兩相一階彎曲振動被同時激發出來時,在彈簧定子中就會疊加合成為一列行波,使定子內表面的各個質點做橢圓運動。

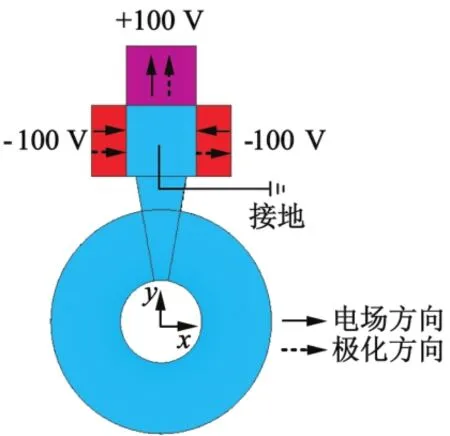
圖3 壓電陶瓷的極化方式

2 定子結構參數的優化設計

由超聲波電動機的驅動原理可知,讓定子產生同頻同型的兩相彎曲振動模態是決定定子內表面各質點能否做橢圓運動的關鍵。但因定子的結構并不是對稱的,所以這兩相一階彎曲振動模態也不是完全相同,如果這兩相一階彎曲振動頻率差異較大就會使超聲波電動機的輸出功率發生波動,從而影響電機的輸出性能,所以必須對彈簧定子的各個結構做相應的優化設計,以達到電機的X,Y相的特征頻率相近的目的。取彈簧定子的中徑(d)、螺距(t)、邊長(b)和外伸梁的長(l)、寬(w)、高(h)6個結構參數為優化變量,對彈簧定子的兩相一階彎曲頻率進行優化,使頻率及其差值滿足要求。

利用標準正交表L8(27)設計正交試驗,結合有限元軟件ANSYS,找出兩相一階彎振頻率及其差值與各設計變量之間的關系。試驗結果如表1所示。

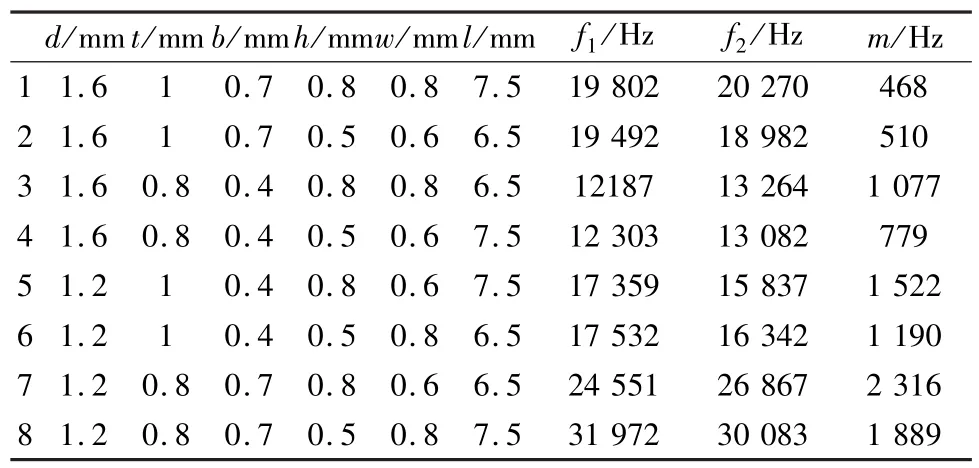
表1 彈簧定子設計變量正交試驗

對正交試驗的結果數據采用多元線性回歸計算處理。

以x向彎振頻率為指標y1,通過計算回歸方程如下:

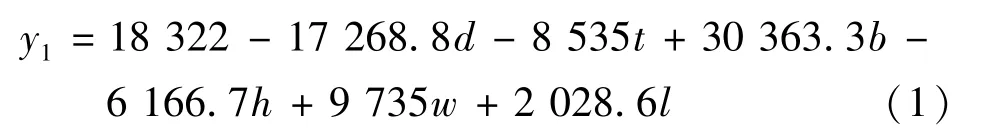
由式(1)可以看出,影響x向彎振頻率的主要因素是彈簧截面邊長b,其次是內徑d與外伸梁寬w。

以y向彎振頻率為指標y2,回歸方程如下:

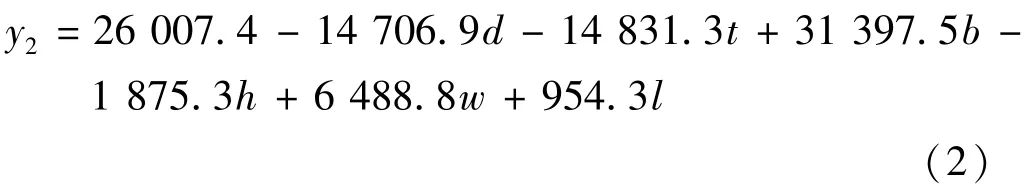
由式(12)可以看出,影響y向彎振頻率的主要因素是彈簧截面邊長b,其次是內徑d與螺距t。

通過多元線性回歸分析可知:彈簧的邊長b、中徑d和螺距t對兩相彎振頻率的影響最大,因此在對彈簧定子各個結構進行優化時優先考慮彈簧的這3個參數的調整。彈簧的邊長b、中徑d和螺距t3個參數對頻率的影響趨勢如圖4所示。

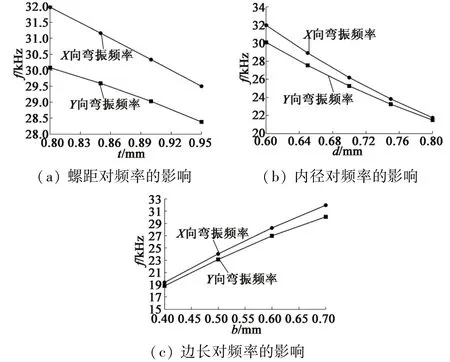
圖4 彈簧參數對頻率的影響圖

綜合以上彈簧定子參數對頻率的影響趨勢與彈簧定子自身幾何尺寸的約束,利用有限元分析軟件ANSYS對彈簧定子各個結構參數進行調整,找到一組綜合性能較好的彈簧定子結構參數的組合,具體尺寸如表2所示。由表2可以看出,優化后,彈簧定子x,y方向的一階彎曲振動模態的固有頻率分別增大至22 396 Hz和22 368 Hz,而頻率差僅為28 Hz,故優化效果明顯。

表2 彈簧定子尺寸優化結果

3 優化后定子運動特性分析

根據表2中的優化后的彈簧定子各個結構參數重新對定子進行建模,并對定子進行模態分析。分析結果如圖5所示,圖5分別表示的是彈簧定子的X,Y相一階彎振模態,即定子的工作模態。由超聲波電動機工作原理可知,只要彈簧定子中激勵出兩相一階彎曲振動,則定子內表面上與轉子相接觸的各個質點就能形成橢圓運動,由此便可通過摩擦力來驅動定子轉動。

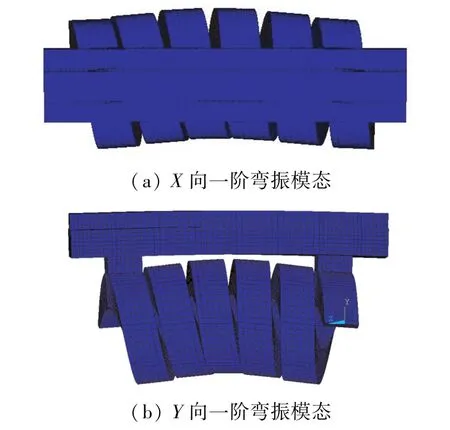
圖5 彈簧定子兩相彎振模態圖

對彈簧定子進行諧響應分析,選取彈簧左端面一個節點作為定子諧響應的分析點,如圖6所示可選取圖中的P4點,繪制該節點的位移隨頻率響應曲線,如圖7所示。

分析可知,由于彈簧結構并不是完全對稱的,導致Y向一階彎曲振動的振幅大于X向振幅,但在頻率為22.37 kHz左右處,定子的兩相振幅基本相同,振幅約1.6 μm,達到驅動轉子的要求。

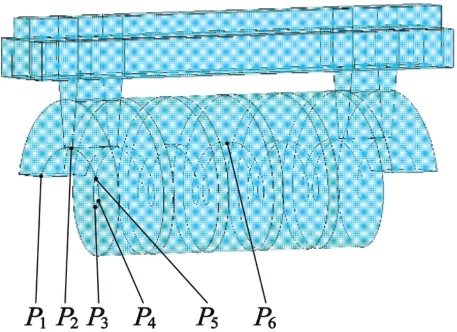
圖6 定子節點選取示意圖

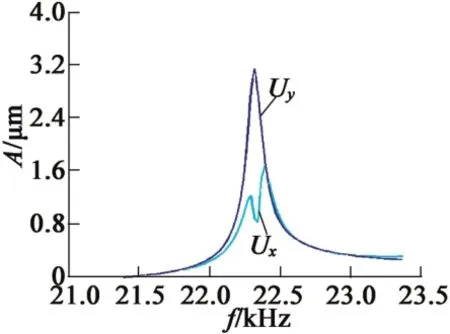
圖7 優化后定子的位移響應曲線

對定子進行瞬態動力學的分析,繪制圖6中的6個節點的運動軌跡,如圖8所示。從圖8中可以看出,6個節點的運動方向均為逆時針,從而確保彈簧定子內表面上各個質點對轉子驅動力方向的一致性。但由于彈簧定子的結構存在不對稱性,橢圓軌跡相對于正橢圓有一定程度的傾斜。其中,P1和P2節點處的橢圓運動發生4處畸變,對轉子的驅動效果有所影響;其余4個節點的橢圓軌跡相比于P1和P2節點更加光滑,并且振幅更大,對轉子的驅動效果好。對行波在定子中的傳播路徑分析可知,因連接板與定子和外伸梁與連接板均是獨立結構彼此連接在一起,行波傳播至這兩個部位時會產生一定突變,并會增大這兩個部位的局部剛度,因此更靠近定子內表面處的4個節點的行波傳播質量更好,振動幅度也更大,橢圓運動軌跡也更加光滑。

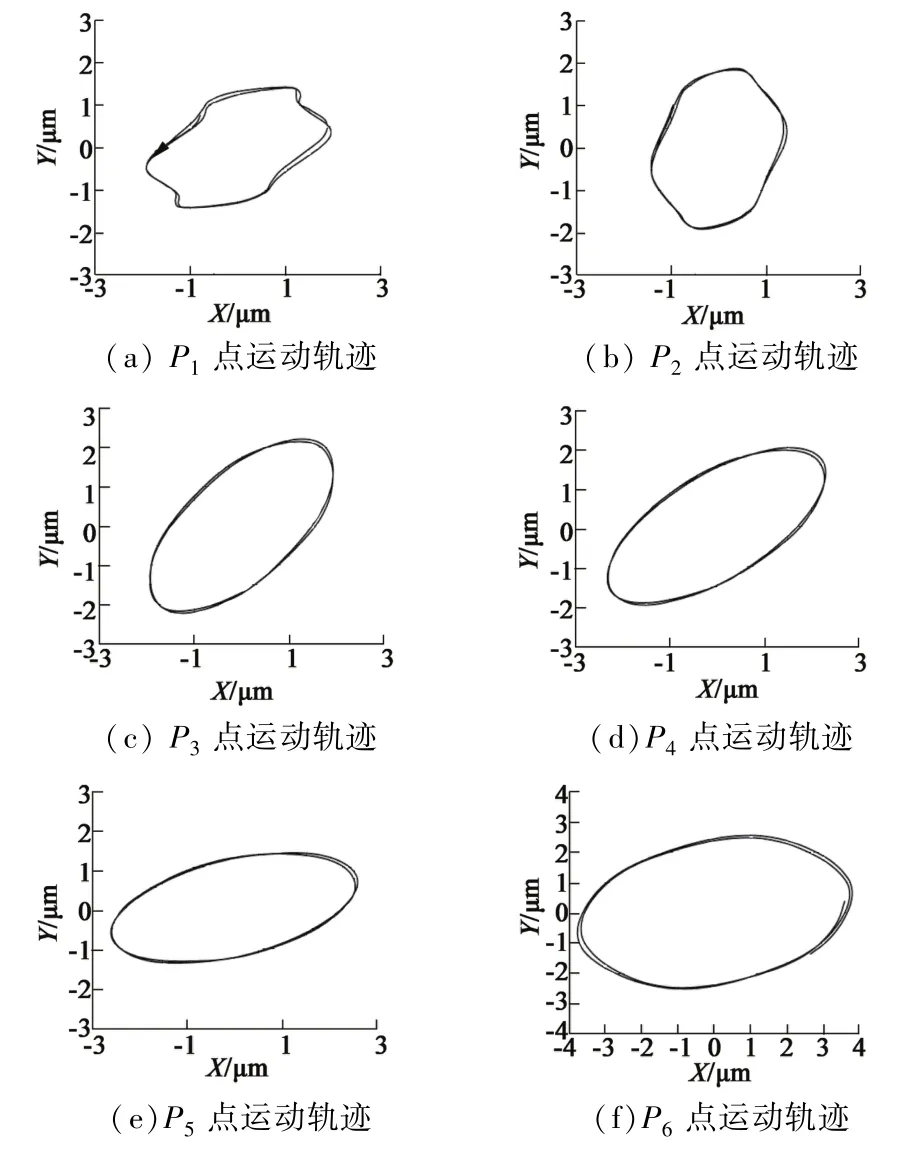
圖8 定子的橢圓運動軌跡

總結:雖然行波在傳播過程中由于定子結構的不規則產生了一定的突變,導致外伸梁附近的一些節點橢圓運動軌跡發生內凹,但定子內表面處的節點橢圓運動軌跡都比較光滑,X與Y向振動的振幅也能達到2 μm,能夠滿足驅動要求。

4 結 語

本文在此前研究的基礎上提出了一種改進結構的彈簧定子超聲波電動機,通過外伸梁結構來解決壓電陶瓷與定子粘接不可靠的問題。設計了該電機的驅動方式,并從理論上分析了驅動面質點有效橢圓運動的存在性;采用正交試驗和ANSYS軟件對定子的結構參數進行優化設計,通過對比,優化后彈簧定子的動力學特性得到較大的提高。

參考文獻

[1] 趙淳生.超聲電機技術與應用[M].北京:科學出版社,2007:1-25.

[2] 趙淳生.21世紀超聲電機技術展望[J].振動、測試與診斷,2000,20(1):7-11.

[3] 陳超,任金華,石明友,等.旋轉行波超聲電機的沖擊動力學模擬及實驗[J].振動、測試與診斷,2014,34(1):8-14.

[4] 趙淳生.世界超聲電機技術的新進展[J].振動、測試與診斷,2004,24(1):1-5.

[5] MORITA T,KUROSAWA M,HIGUCHI T.An ultrasonic motor using a bending cylindrical transducer based on PZT thin film[J].Sensors and actuators,1995,50(1-2):75-80.

[6] DONG S X,LIM S P,LEE K H,et al.Piezoelectric ultrasonic micromotor with 1.5mm diameter[J].IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control,2003,50(4):361-367.

[7] 朱華,陳超,趙淳生.一種微型柱體超聲電機的研究[J].中國電機工程學報,2006,26(12):128-133.

[8] 王天華,張輝.1mm管式懸臂梁結構微型超聲馬達研究[J].南京大學學報學報,2007,43(4):419-425.

[9] MORIYA T,AKANO Y,FURUKAWA Y,NAKAJIMA A.Development of a miniature ultrasonic motor using a helical coil as a stator[C]//IEEE Ultrasonic Symposium,2005:1546-1549.

[10] 董迎暉,顧雅春,湯開元,等.采用彎曲振動模態的彈簧定子超聲電機[J].振動、測試與診斷,2013,33(157):13-16.