汽車驅動橋系統模態綜合動力學建模與分析

周 馳， 丁煒琦， 桂良進， 范子杰

(1.清華大學 汽車工程系 汽車安全與節能國家重點實驗室，北京 100084； 2.陜西漢德車橋有限公司，西安 710201)

汽車驅動橋系統模態綜合動力學建模與分析

周 馳1， 丁煒琦2， 桂良進1， 范子杰1

(1.清華大學 汽車工程系 汽車安全與節能國家重點實驗室，北京 100084； 2.陜西漢德車橋有限公司，西安 710201)

提出一種汽車驅動橋系統的模態綜合動力學建模與分析方法，采用非線性軸承單元實現傳動系模型與橋殼模型的耦合建模，采用模態綜合法對驅動橋各部件的有限元模型進行縮維變換，能夠在準確模擬驅動橋系統動力學特性的同時大大縮減系統模型規模，從而快速準確地實現驅動橋系統的靜力學非線性求解和動力學分析。以準雙曲面齒輪有限元接觸分析求得的動態嚙合力作為系統激勵，計算驅動橋系統的動力學響應，并進行試驗驗證，數值計算結果能夠準確體現準雙曲面齒輪動態嚙合力激勵下的驅動橋系統動力學特性，有效指導驅動橋的減振降噪設計。

驅動橋；模態綜合法；準雙曲面齒輪；動力學分析

驅動橋是汽車的核心動力總成和主要的振動噪聲源，驅動橋系統的振動噪聲會影響汽車的可靠性、乘員的舒適性和運輸的安全性[1]。準雙曲面齒輪廣泛用于驅動橋主減速器傳動系統，齒輪嚙合過程中產生的動態激勵是驅動橋系統振動噪聲的主要原因[2]。現有研究大多采用集中參數模型對準雙曲面齒輪系統進行動力學建模與分析[3-5]，對橋殼和軸承等部件的模擬過于簡化，無法準確體現驅動橋系統的動力學特性。有學者采用有限元接觸分析方法計算驅動橋系統的動態響應，但驅動橋有限元模型包含大量接觸關系，建模過程十分復雜，系統模型的規模巨大，接觸分析需要消耗大量的計算資源，分析效率和收斂性很低[6]。另有學者在驅動橋系統有限元建模時對滾動軸承模型進行了簡化，無法準確體現滾動軸承的非線性剛度特性[7-8]。

周馳等提出了一種基于空間梁單元理論的驅動橋系統動力學建模分析方法，并采用非線性滾子軸承單元實現了傳動系與橋殼模型的耦合建模，能夠快速實現驅動橋系統的動力學分析，但空間梁單元模型對齒輪輪齒和十字軸等局部特征進行了等效，且采用的傳統等效嚙合模型求得的準雙曲面齒輪嚙合參數沒有考慮齒面摩擦的影響，動力學分析時采用的單位諧波傳動誤差激勵較為簡化，建模和分析的精度有待進一步提高。本文在文獻[9]的基礎上，提出一種更準確和通用的汽車驅動橋系統模態綜合動力學建模和分析方法，建立更為準確的驅動橋系統動力學分析模型，并以準雙曲面齒輪有限元接觸分析求得的動態嚙合力作為系統的激勵源，準確計算驅動橋系統的動力學響應，并進行試驗驗證。

1 驅動橋系統部件有限元建模

圖1為典型商用車后驅動橋的幾何模型，發動機后置，規定前進方向為全局坐標系X軸的正向，左側為Y軸的正向，豎直向上為Z軸的正向，坐標原點O取在輪間差速器的十字軸中心位置。圖2為驅動橋傳動系的二維示意圖。

圖1 驅動橋幾何模型

1-差速器左側圓錐滾子軸承；2-左半軸；3-左車輪；4-左輸出轉矩；5-左輸出端扭轉剛度；6-左輸出端轉動慣量；7-左車輪外側圓錐滾子軸承；8-左車輪內側圓錐滾子軸承；9-左太陽輪；10-行星輪；11-小輪軸；12-輸入端扭轉剛度；13-輸入端轉動慣量；14-輸入轉矩；15-傳動軸凸緣；16-小輪軸后端圓錐滾子軸承；17-小輪軸中部圓錐滾子軸承；18-小輪軸前端圓柱滾子軸承；19-右太陽輪；20-右半軸；21-右車輪內側圓錐滾子軸承；22-右車輪；23-右車輪外側圓錐滾子軸承；24-右輸出端轉動慣量；25-右輸出端扭轉剛度；26-右輸出轉矩；27-差速器右側圓錐滾子軸承；28-差速器殼；29-大輪；30-十字軸

圖2 驅動橋傳動系示意圖

Fig.2 Schematic of drive axle transmission system

1.1 傳動系部件有限元模型

建立傳動系部件的體單元有限元模型，如圖3～圖9所示，單元類型為四節點四面體單元，材料參數為部件的真實材料參數。為了實現后續模態綜合縮維計算和模型之間的連接，需要在有連接關系的位置建立邊界節點，以邊界節點作為主節點，采用剛性連接單元(RBE2)與部件有限元模型的體單元節點耦合。傳動系各部件的邊界節點建立如下：

(1) 傳動軸凸緣模型建立兩個邊界節點，如圖3所示，1號節點為花鍵連接節點，2號節點為輸入轉矩加載點；

(2) 小輪軸模型建立5個邊界節點，如圖4所示，1號～3號節點為軸承連接點，4號節點為齒輪等效嚙合節點，5號節點為花鍵連接節點；

(a) 有限元模型

(b) 邊界節點

(a) 有限元模型

(b) 邊界節點

(a) 有限元模型

(b) 邊界節點

圖5 大輪及差速器殼模型

Fig.5 Finite element models of wheel and differential case

(a) 有限元模型

(b) 邊界節點

(a)有限元模型(b)邊界節點

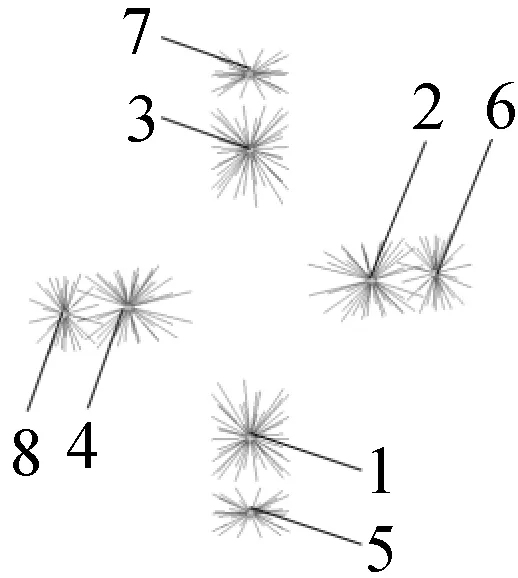
(3) 大輪與差速器殼模型采用共用節點的方法連接，用來模擬螺栓連接，建立9個邊界節點，如圖5所示，1號和2號節點為軸承連接節點，3號節點為準雙曲面齒輪等效嚙合節點，4號和5號節點為墊片連接節點，6號～9號節點為差速器殼十字軸孔連接節點；

(4) 十字軸模型建立8個邊界節點，如圖6所示，1號～4號節點為行星輪旋轉副連接節點，5號～8號節點為差速器殼十字軸孔連接節點；

(a)有限元模型(b)邊界節點

圖8 太陽輪模型

圖9 半軸及輪轂模型

Fig.9 Finite element models of half shafts and hubs

(5) 差速器共有4個行星輪，每個行星輪模型建立3個邊界節點，如圖7所示，1號和2號節點為等效嚙合節點，3號節點為旋轉副連接節點；

(6) 每個太陽輪模型建立6個邊界節點，如圖8所示，1號～4號節點為等效嚙合節點，5號節點為花鍵連接節點，6號節點為差速器殼墊片連接節點；

(7) 半軸與車輪模型采用共用節點的方式連接，用來模擬螺栓連接，左右兩側模型均建立4個邊界節點，如圖9所示，1號和2號節點為軸承連接節點，3號節點為花鍵連接節點，4號節點為輸出轉矩加載點。

1.2 橋殼有限元模型

橋殼有限元模型如圖10所示，在9個滾動軸承的中心位置均建立邊界節點，并分別通過剛性連接單元與軸承座表面的節點耦合。為了與試驗對比，在加速度測點位置也建立邊界節點。約束板簧位置的節點自由度，模擬振動試驗臺對橋殼的支承。

圖10 橋殼有限元模型

1.3 非線性滾動軸承模型

滾動軸承是連接傳動系和橋殼的關鍵部件，采用非線性軸承單元[10]耦合對應的傳動系模型邊界節點自由度與橋殼邊界節點自由度，如圖11所示。

圖11 滾動軸承模型示意圖

1.4 齒輪嚙合模型

本文驅動橋為準雙曲面齒輪傳動，齒輪參數如表1所示，采用有限元分析軟件ABAQUS建立準雙曲面齒輪有限元接觸分析模型[11-13]，如圖12所示，對5對齒輪進行接觸分析即可求得準雙曲面齒輪一個嚙合周期的等效嚙合參數[14]。根據試驗轉矩工況，在小輪模型中心施加轉矩Tp=-1 257 N·m，齒面摩擦因數取0.1[15]，求得的準雙曲面齒輪等效嚙合參數如表2所示。

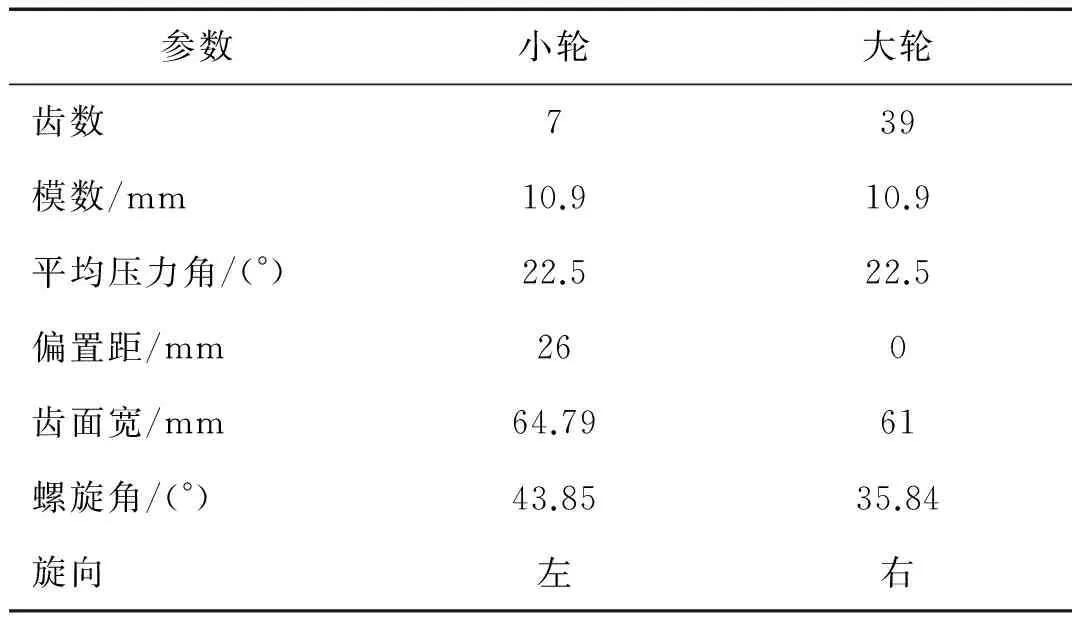
表1 準雙曲面齒輪參數

圖12 準雙曲面齒輪有限元模型

參數X分量Y分量Z分量等效嚙合點坐標/mm-180.97-14.2417.67等效嚙合力方向向量0.535-0.5640.629等效嚙合剛度/(MN·mm-1)1.628

差速器齒輪的等效嚙合參數采用文獻[9]中的方法求得。基于齒輪等效嚙合參數，可以進一步計算齒輪的嚙合剛度矩陣。

有限元接觸分析求得的大輪動態嚙合力如圖13所示，小輪動態嚙合力與大輪大小相等，方向相反，該動態嚙合力即為驅動橋系統動力學分析的激勵源。

圖13 準雙曲面齒輪等效嚙合力

1.5 連接部件模型

對傳動系部件之間的連接關系進行模擬，包括：傳動軸凸緣與小輪軸之間的花鍵連接、太陽輪與半軸之間的花鍵連接、十字軸與差速器殼十字軸孔之間的連接、十字軸與行星輪之間的旋轉副連接、太陽輪與差速器殼之間的墊片連接。上述連接關系均采用線性彈簧單元模擬，剛度矩陣表示為式(1)的形式

Kc=diag([kδXkδYkδZkθXkθYkθZ])

(1)

式中:kδX、kδY和kδZ為各方向的平動剛度；kθX、kθY和kθZ為各方向的轉動剛度。

2 驅動橋系統模態綜合動力學建模

采用固定界面模態綜合法[16]對各部件的有限元模型進行縮維，僅保留邊界節點自由度和體現內部節點自由度振動特性的主模態自由度，有限元模型縮維后的模態綜合剛度矩陣KM和模態綜合質量矩陣MM如式(2)和式(3)所示

(2)

(3)

式中:KFE和MFE分別為原始有限元模型的剛度矩陣和質量矩陣；kcc為邊界自由度對應的剛度矩陣；knc和kcn為邊界自由度與主模態自由度之間的剛度耦合項；knn為主模態自由度對應的剛度矩陣；mcc為邊界自由度對應的質量矩陣；mnc和mcn為邊界自由度與主模態自由度之間的質量耦合項；mnn為主模態自由度對應的質量矩陣；Φ為模態綜合變換矩陣，如式(4)所示

(4)

假設部件A與部件B的模態綜合模型之間存在連接關系，連接單元的剛度矩陣為KC，則邊界節點自由度剛度項KA和KB的耦合關系如式(5)所示

(5)

由式(5)的方法將各部件的剛度矩陣和質量矩陣按照連接關系組集，獲得驅動橋系統的剛度矩陣K和質量矩陣M，完整驅動橋系統模態綜合模型的動力學方程如式(6)所示

(6)

由于滾動軸承單元具有非線性特性，將對應轉矩工況靜平衡時的軸承切線剛度矩陣作為動力學模型的線性軸承剛度。

完整驅動橋系統的有限元模型共包含235 150個節點，而本文建立的驅動橋系統模態綜合動力學模型共有1 034個自由度，自由度大幅度減小，對比模態綜合模型與有限元模型求得的驅動橋系統2 000 Hz以內的固有振動頻率，最大相對誤差為4.99%，大部分在2%以內，說明驅動橋模態綜合動力學模型良好地保留了原有限元模型的動力學特性。

3 驅動橋系統動力學分析與試驗驗證

采用有限元接觸分析方法求得的主減速器齒輪動態嚙合力在一個周期內的離散數據可以表示為式(7)所示傅里葉級數形式

(7)

(8)

式中:zp為小輪齒數；np為小輪轉速,r/min；頻率的單位為Hz。

60 km/h車速試驗工況對應的輸入轉速np=1 671 r/min，由式(8)求得準雙曲面齒輪基頻f0=195 Hz。對圖13中的一個周期嚙合力數據進行式(7)所示的傅里葉級數變換，求得各階齒輪激振頻率對應的嚙合力幅值A和相位B如圖14和圖15所示，傅里葉變換求得的直流分量即為等效嚙合力的平均值，X、Y、Z三個方向的直流分量分別為32.28 kN、34.04 kN和37.96 kN。

圖14 準雙曲面齒輪等效嚙合力幅值

圖15 準雙曲面齒輪等效嚙合力相位

(9)

式中:ω和φ分別為驅動橋系統的固有振動圓頻率和正則振型；ωdk為齒輪嚙合力第k階激振圓頻率；ωi為驅動橋系統的第i階固有振動圓頻率；λi=ωdk/ωi為第i階頻率比；ξi為第i階模態阻尼比，計算時取0.02；n為模態疊加法保留的驅動橋系統模態階數。

驅動橋系統總位移響應即為式(9)各階響應的疊加，如式(10)所示

(10)

式中，NF為動態嚙合力包含的頻率階數。

測量驅動橋在穩定運轉過程中橋殼上的加速度響應，在橋殼頂部和后蓋分別布置加速度傳感器，如圖16所示，試驗工況為60 km/h車速滑行工況，輸入轉矩Tp=-1 257 N·m，輸入轉速np=1 671 r/min。

圖16 驅動橋振動響應試驗

對比本文數值計算與試驗測得的時域法向振動加速度曲線如圖17和圖18所示，結果較為一致。

圖17 橋殼上方測點法向振動加速度

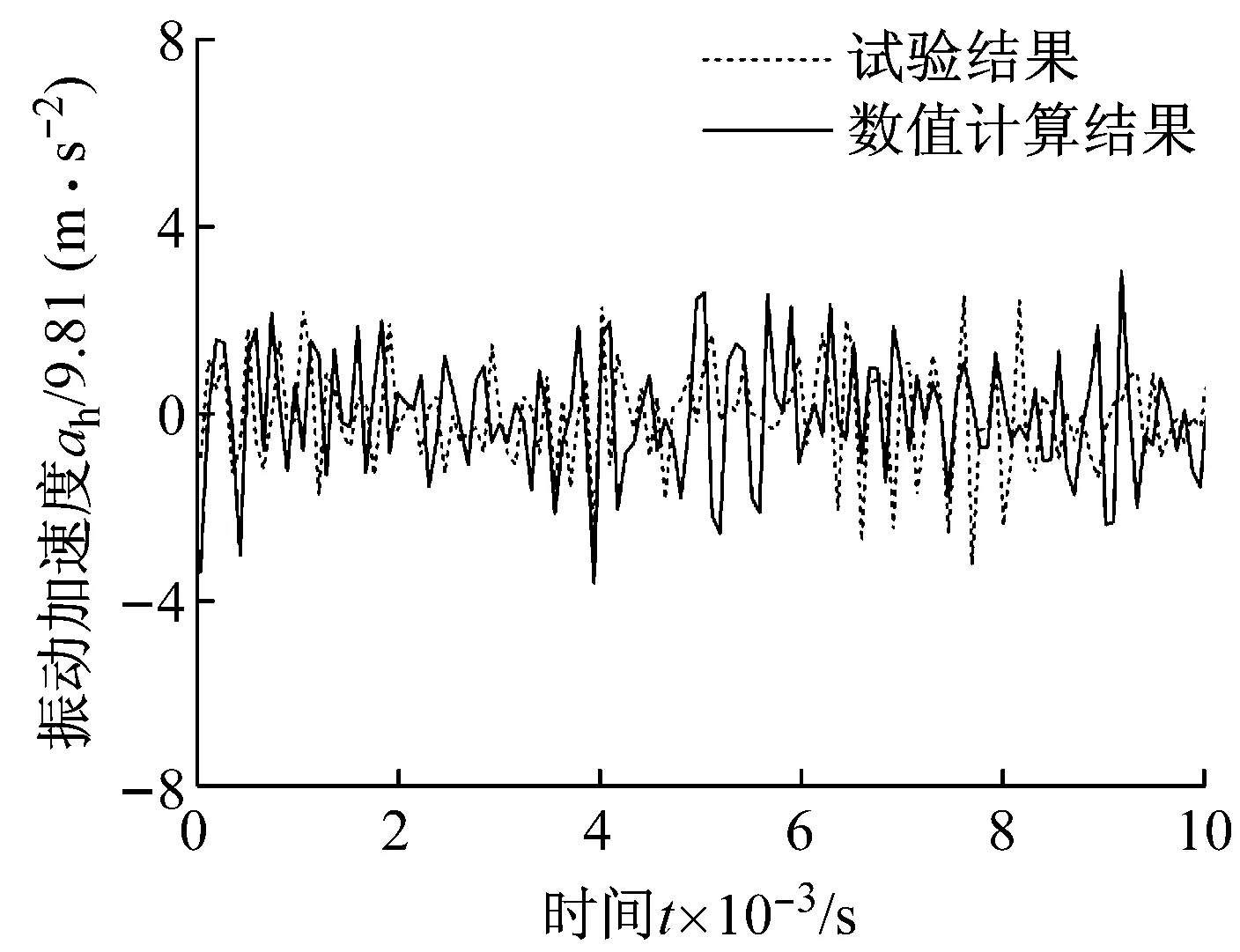
圖18 后蓋測點法向振動加速度

進一步對比上述時域振動加速度的均方根值，如表3所示，數值計算結果與試驗結果的相對誤差在15%左右，吻合程度較為理想，驗證了本文驅動橋系統動力學建模和分析方法的正確性。

表3 振動加速度均方根值

振動加速度的幅值譜分析結果如圖19和圖20所示， 因為主減速器齒輪的動態嚙合激勵是驅動橋系統振動噪聲的最主要原因，數值計算與試驗結果均較為明顯地體現出準雙曲面齒輪嚙合激勵的基頻和倍頻成分，且一致性良好。

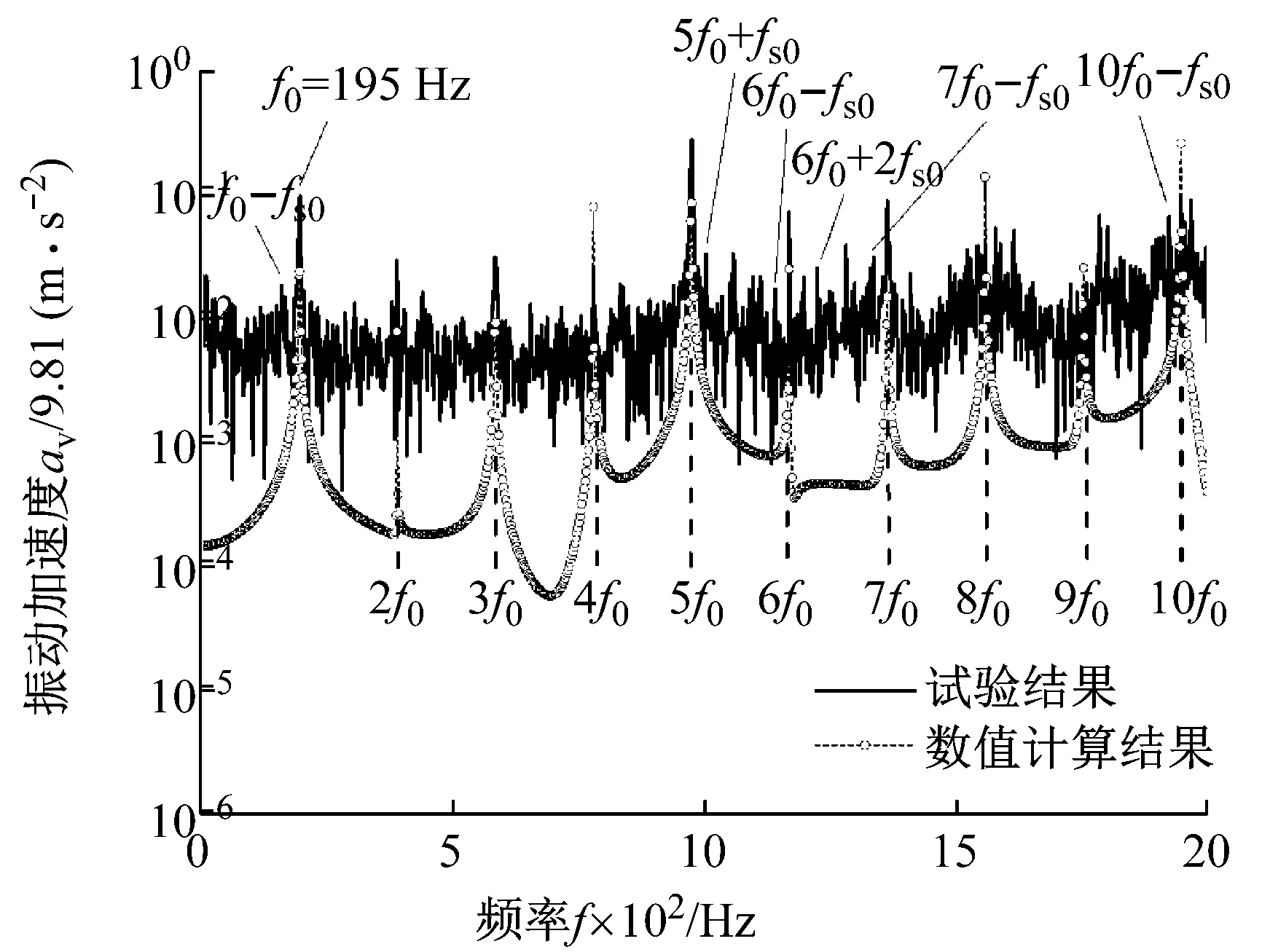
圖19 橋殼上方法向振動加速度幅值譜

Fig.19 Vibration acceleration amplitude spectrum on the top of the housing

圖20 后蓋測點法向振動加速度幅值譜

Fig.20 Vibration acceleration amplitude spectrum on the rear cover

在試驗過程中，如果輸入軸不平衡，也會對驅動橋系統產生動態激勵，輸入軸不平衡激振的基頻fs0如式(11)所示，ns為輸入軸的轉速，r/min，60 km/h車速工況對應的fs0為27.85 Hz。

(11)

在圖19和圖20中的試驗振動加速度幅值譜分析結果中，輸入軸不平衡激勵主要以齒輪激振頻率和輸入軸激振頻率的組合形式體現，圖19中可以觀察到f0-fs0、5f0+fs0、6f0-fs0、6f0+fs0、6f0+2fs0、7f0-fs0和10f0-fs0等組合頻率峰值，圖20中可以觀察到f0-fs0、2f0+fs0、2f0+2fs0、4f0+fs0、5f0+fs0、6f0-fs0、6f0+fs0、6f0+2fs0和10f0-fs0等組合頻率峰值。

4 結 論

本文通過汽車驅動橋系統的模態綜合動力學建模與分析，獲得如下結論：

(1) 提出了一種驅動橋系統模態綜合動力學建模和分析方法，能夠在準確模擬驅動橋系統動力學特性的同時大大縮減系統模型規模，以有限元接觸分析方法求得的準雙曲面齒輪動態嚙合力作為驅動橋系統的激勵源，能夠準確實現驅動橋系統的動力學分析。

(2) 驅動橋殼體測點的振動加速度數值計算結果與試驗結果吻合良好，驗證了本文方法的正確性，振動加速度幅值譜的峰值頻率能夠良好地體現出準雙曲面齒輪嚙合激勵特性。

(3) 本文方法基于可靠的理論基礎，且易于通過商用軟件和編程實現，具有較高的計算效率，能夠準確快速地實現驅動橋系統的動力學建模與分析，有效指導驅動橋的減振降噪設計，并可廣泛用于其他齒輪傳動系統的設計建模與計算分析。

[1] 劉惟信. 汽車車橋設計[M]. 北京: 清華大學出版社，2004:5-22.

[2] DONLEY M G, LIM T C, STEYER G C. Dynamic analysis of automotive gearing systems[C]// Detroit： SAE International Congress and Exposition, 1992:77-87.

[3] LIM T C, CHENG Y. A theoretical study of the effect of pinion offset on the dynamics of hypoid geared rotor system[J]. Journal of Mechanical Design, 1999, 121(4):594-601.

[4] CHENG Y, LIM T C. Vibration analysis of hypoid transmissions applying an exact geometry-based gear mesh theory[J]. Journal of Sound and Vibration, 2001, 240(3):519-543.

[5] CHENG Y, LIM T C. Dynamics of hypoid gear transmission with nonlinear time-varying mesh characteristics[J]. Journal of Mechanical Design, 2003, 125(2):373-382.

[6] 郭年程, 史文庫, 劉文軍, 等. 驅動橋的整體有限元動態模擬[J]. 西安交通大學學報, 2012, 46(9):91-95.

GUO Niancheng, SHI Wenku, LIU Wenjun, et al. Dynamic simulation of driving axle based on finite element method[J]. Journal of Xi’an Jiaotong University, 2012, 46(9):91-95.

[7] 張健. 汽車驅動橋振動噪聲研究[D]. 重慶: 重慶大學, 2005.

[8] 晏慧. 重型商用車驅動橋振動噪聲預測研究[D]. 重慶: 重慶大學, 2010.

[9] 周馳, 丁煒琦, 桂良進, 等. 一種驅動橋齒輪傳動系統動力學建模與分析方法[J]. 振動與沖擊, 2015, 34(15):188-194.

ZHOU Chi, DING Weiqi, GUI Liangjin, et al. Dynamic modeling and analysis for drive axle gear transmission system[J]. Journal of Vibration and Shock, 2015, 34(15):188-194.

[10] 田程, 周馳, 桂良進, 等. 考慮軸承剛度耦合性和非線性的多支撐軸系有限元分析方法[J]. 機械工程學報，2015, 51(17):90-95.

TIAN Cheng, ZHOU Chi, GUI Liangjin, et al. A method of finite element analysis for multi-support shaft system base on the coupling and nonlinearity of bearing stiffness[J]. Journal of Mechanical Engineering, 2015, 51(17):90-95.

[11] LITVIN F L, ZHANG Y. Local synthesis and tooth contact analysis of face-milled spiral bevel gears: ARL-CR-312[R]. Illinois: University of Illinois at Chicago, 1991.

[12] LITVIN F L, FUENTES A. Gear geometry and applied theory[M]. 2nd ed. Cambridge: Cambridge University Press, 2004:679-696.

[13] Stiffness calculations based on the finite element method[J]. Journal of Mechanical Engineering, 2011, 47(11): 23-29.

[14] PENG T. Coupled multi-body dynamic and vibration analysis of hypoid and bevel geared rotor system[D]. Cincinnati: University of Cincinnati, 2010.

[15] HARRIS T A, KOTZALAS M N. Essential concepts of bearing technology[M]. 5th ed. Beijing: CRC Press, 2006:86.

[16] CRAIG R R, BAMPTON M C C. Coupling of substructures for dynamic analyses[J]. AIAA Journal, 1968, 6(7):1313-1319.

Modal synthesis dynamic modeling and analysis for an automotive drive axle system

ZHOU Chi1, DING Weiqi2, GUI Liangjin1, FAN Zijie1

(1. State Key Laboratory of Automotive Safety and Energy, Department of Automotive Engineering, Tsinghua University, Beijing 100084, China; 2. Shaanxi Hande Axle Co., Ltd., Xi’an 710201, China)

A modal synthesis dynamic modeling and analysis method for an automotive drive axle system was proposed. The transmission system model and the housing model were coupled with nonlinear bearing elements. In order to realize static nonlinear solving and dynamic analysis of the drive axle system quickly and accurately, finite element models of its components were condensed with the modal synthesis method. Meshing forces of a couple of hypoid gears were calculated based on the finite element contact analysis method. The dynamic responses of the drive axle system excited by the meshing forces of the couple of hypoid gears were calculated and verified with tests. The numerical analysis results revealed the dynamic characteristics of the drive axle system under the excitation of the meshing forces of the couple of hypoid gears correctly and guided the vibration and noise reduction design of the drive axle effectively.

drive axle; modal synthesis method; hypoid gear; dynamic analysis

校企合作項目(20142000237)

2016-01-15 修改稿收到日期：2016-03-15

周馳 男，博士，1986年生

范子杰 男，教授，博士生導師，1958年生

TH132.46；U463.218

A

10.13465/j.cnki.jvs.2017.09.002