基于性能的相鄰結構間Maxwell阻尼器優化布置研究

吳巧云， 朱宏平， 陳旭勇

(1.武漢工程大學 資源與土木工程學院，武漢 430073; 2.華中科技大學 土木工程與力學學院，武漢 430074)

基于性能的相鄰結構間Maxwell阻尼器優化布置研究

吳巧云1,2， 朱宏平2， 陳旭勇1,2

(1.武漢工程大學 資源與土木工程學院，武漢 430073; 2.華中科技大學 土木工程與力學學院，武漢 430074)

對連接Maxwell模型的兩相鄰鋼筋混凝土框架結構進行了基于性能的阻尼器優化布置研究。以使兩相鄰結構總超越概率最小為優化目標，對確定阻尼器數目下的相鄰結構進行了阻尼器優化布置位置的研究，得出了相鄰結構間Maxwell阻尼器的優化位置的一般布置規律。通過連接不同優化布置位置的Maxwell阻尼器的相鄰結構地震易損性分析，得出了相鄰結構間連接Maxwell阻尼器的優化數目。所得相鄰結構間阻尼器的優化布置，可以使相鄰結構在不同性能目標的地震作用下均能得到較優的控制效果，為實際工程的應用作出了有益探討。

相鄰結構；Maxwell阻尼器；優化位置；優化數目；地震易損性；超越概率

為了防止間距較近的相鄰結構在強震作用下發生碰撞，許多學者提出了在相鄰結構之間安裝被動控制裝置的思想，利用相鄰結構之間的相對振動來消耗或吸收部分能量，以達到減振的目的。朱宏平等[1]提出了一種利用主從結構間的相互作用來減小地震響應的控制方法，推導了在平穩白噪聲激勵下被動耗能單元的優化剛度和優化阻尼的一般表達式，并分析了不同結構參數對控制效果的影響；隨后,朱宏平等[2]將相鄰結構簡化為兩單自由度體系，用Voigt黏彈性阻尼模型表示被動連接單元，運用Kuhn-Tucker優化原理導出了在地面隨機激勵下被動連接單元的優化剛度和阻尼值的一般表達式；此后，朱宏平等[3-5]又基于能量統計原理分別推導了雙體單自由度體系間Kelvin型和Maxwell型阻尼器優化參數的解析表達式。后來，Zhu等[6]將基于相鄰單自由度結構體系推導的阻尼器優化參數表達式推廣到了相鄰多自由度結構體系，得出阻尼器的優化參數與相鄰結構的第一階自振頻率和總質量有關的推論。Zhang等[7]用Maxwell模型模擬液體阻尼器連接相鄰結構，通過解決不對稱矩陣特征值來分析動力特性，將狀態空間法和虛擬激勵法相結合確定隨機地震響應，指出通過選擇合適的阻尼系數可以提高模態阻尼比，并有效降低結構的地震響應。Bhaskararao等[8]將基底加速度模擬成簡諧振動和平穩高斯白噪聲隨機激勵，對連接黏滯阻尼器的兩相鄰線性單自由度體系的動力響應進行了研究。推導了結構的運動方程并求出了相鄰結構的相對位移和絕對加速度響應。結果表明當黏滯阻尼器具有合適的阻尼時可以減小相鄰結構間的地震響應。Quinonero等[9]提出了一種基于靜態輸出反饋控制的控制器，可以使相鄰結構得到有效的振動控制，并且該控制器可以由線性被動控制裝置實現。數值模擬結果表明了該控制器的有效性。Park等[10]提出了一種優化混合控制方法減小相鄰結構的地震響應：被動控制裝置布置在相鄰結構之間；主動控制裝置布置在結構中的兩塊連續樓板之間。通過數值算例證實所提混合控制策略可同時實現控制性能和控制成本的最優化。

振動控制的效果不僅取決于相鄰結構間阻尼器的設置參數，也取決于阻尼器在相鄰結構中的布置方式，對控制裝置進行布置優化是非常有必要的。然而，以往眾多振動控制的研究將重點放在控制裝置的參數優化上，即便文獻[11-12]進行過控制裝置的優化布置研究，但主要局限在線彈性分析狀態，所提出的控制裝置的優化布置能否使得相鄰結構在不同性能目標的地震作用下均具有良好的控制效果，值得進一步深入研究。

本文對連接Maxwell型阻尼器的兩相鄰鋼筋混凝土框架結構進行了基于性能的阻尼器優化布置研究。以使兩相鄰結構總超越概率最小為優化控制目標，首先提出了確定數目下阻尼器的優化布置位置；然后對連接不同數目、采用優化布置的阻尼器的相鄰結構進行了地震易損性分析，得到了合理的阻尼器優化布置數目。通過本文研究，提出了相鄰結構間連接Maxwell阻尼器的優化布置的一般規律，為實際工程的應用作出了有益探討。另外，本文所建議的Maxwell阻尼器的優化布置能使得相鄰結構在各性能目標的地震作用下均具有優良的控制效果，可以使相鄰結構滿足多目標抗震設防的需要，這是優于以往其它關于阻尼器優化布置研究的。

1 相鄰結構計算模型及地震記錄的選取

1.1 相鄰結構計算模型

本文算例所選模型為文獻[13]中的相鄰結構計算模型。結構1為10層鋼筋混凝土框架，結構2為6層鋼筋混凝土框架，結構平立面布置均勻，為簡化計算，兩結構各取其中一榀建立二維模型。相鄰結構計算模型如圖1所示。兩結構主要設計參數如下：建筑場地II類，抗震設防烈度為8度，設計基本地震加速度為0.20g，設計地震分組第二組，框架抗震等級結構1為一級，結構2為二級,基本風壓0.35為kN/m2，基本雪壓為0.25 kN/m2,混凝土強度等級柱、梁、樓板均為C35,梁、柱主筋HRB335級，箍筋HPB300級,結構層高均為3.6 m,結構1截面尺寸為梁300 mm×800 mm,柱750 mm×750 mm,結構2截面尺寸為梁300 mm×800 mm,柱800 mm×800 mm,各結構樓板厚100 mm。相鄰結構計算簡圖見圖1。圖1亦給出了相鄰結構底層柱的配筋情況。

(a)(b)

圖1 相鄰結構計算模型

Fig.1 Calculation model of the adjacent structures

采用OpenSees程序對該結構建立二維模型并進行增量動力分析(Incremental Dynamic Analysis, IDA)。Maxwell阻尼器材料選用uniaxialMaterial Maxwell模擬。梁、柱及Maxwell阻尼器選用基于位移的非線性纖維梁柱單元模擬。采用OpenSees分析得到結構1的第一階自振頻率ω1=8.418 rad/s，結構2第一階自振頻率ω1=17.525 4 rad/s。結構1總質量為303.070 5 t，結構2總質量為203.802 1 t。

1.2 地震記錄的選取

Shome[14]曾研究過，對于中等高度的建筑，選取10～20條地震記錄進行增量動力分析可以得到較為精確的地震需求估計。參見文獻[15]的地震動選取原則，算例所處場地為《建筑抗震設計規范》(GB 5011—2010)[16]中所規定的II類場地，故通過美國太平洋地震研究中心的數據庫，本文選取了相當于II類場地的20條震級在6.5～6.9的實際遠場地震記錄。分析中不考慮地震動的空間差動效應且僅考慮水平向地震動。

2 被動控制單元及優化問題的描述

2.1 被動控制單元

選擇Maxwell型阻尼器作為被動控制單元。Maxwell阻尼器由阻尼元件與彈簧串聯組成，當阻尼裝置表現出具有依賴頻率的性質時，選用Maxwell模型可以得到較為精確的結果。Maxwell阻尼器產生的控制力計算公式為

(1)

Maxwell模型具有非線性特性，可以模擬相鄰結構在進入彈塑性變形階段時控制裝置的非線性行為，本文采用非線性纖維梁柱單元模擬Maxwell阻尼器，阻尼器材料選用uniaxialMaterialMaxwell模擬。

2.2 控制單元優化參數

文獻[13]的研究中曾指出，若使相鄰結構在不同性能目標的地震作用下均具有良好的控制效果，所連接的Maxwell阻尼器優化參數的設置不宜采用文獻[6]中優化參數解析表達式計算出的控制裝置參數值。本文參考文獻[13]選取Maxwell阻尼器阻尼優化參數值1.5×105N·s/m。此外，因Maxwell阻尼器的剛度系數對相鄰結構控制效果的影響很小，因此剛度系數仍采用文獻[6]中優化參數解析表達式計算出的值5.914×105N/m進行基于性能的相鄰結構間阻尼器的優化布置研究,阻尼指數值取0.5。

2.3 優化布置問題的描述

控制目標為盡可能的減小兩結構總的地震響應，將目標函數取為兩結構總的超越概率，并將該目標函數以P表示，則Maxwell阻尼器的優化布置問題可表達為

(2)

(3)

式中，Pi(EDPi>y|IM=im)(i=1,2)為結構i在任意給定地震動強度IM=im水平下,地震工程需求參數EDP超越性能目標y的概率。

分兩步對Maxwell阻尼器進行優化布置研究：第一步為Maxwell阻尼器布置位置的優化；第二步為Maxwell阻尼器布置數目的優化。

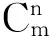
在第二步中，將連接不同數目且采用優化布置阻尼器的相鄰結構在不同性能目標下的總超越概率進行比對，選取相鄰結構總超越概率最小所對應的阻尼器數目，即為Maxwell阻尼器的最優布置數目。

通過這兩步，Maxwell阻尼器在任何性能目標下的布置位置和數目均進行了優化，同時也得出了Maxwell阻尼器在相鄰結構振動控制體系中優化布置的一般規律。

3 算例分析

3.1 結構性能目標y的確定

選取可以表征結構整體破壞指標的最大層間位移角作為工程需求參數(Engineering Demand Measure, EDP)，選取峰值加速度為地震動強度指標(Intensity Measure, IM)，將結構的極限狀態劃分為立即使用(Immediately Occupation, IO)、輕微破壞(Slightly Damage, SD)、生命安全(Life Safety, LS)和防止倒塌(Collapse Prevention, CP)四個狀態，各極限狀態對應的性能目標見表1[17]。

表1 各性能極限狀態下的性能目標y

3.2 Maxwell阻尼器布置位置的優化

3.2.1 不同布置位置組合下相鄰結構的超越概率

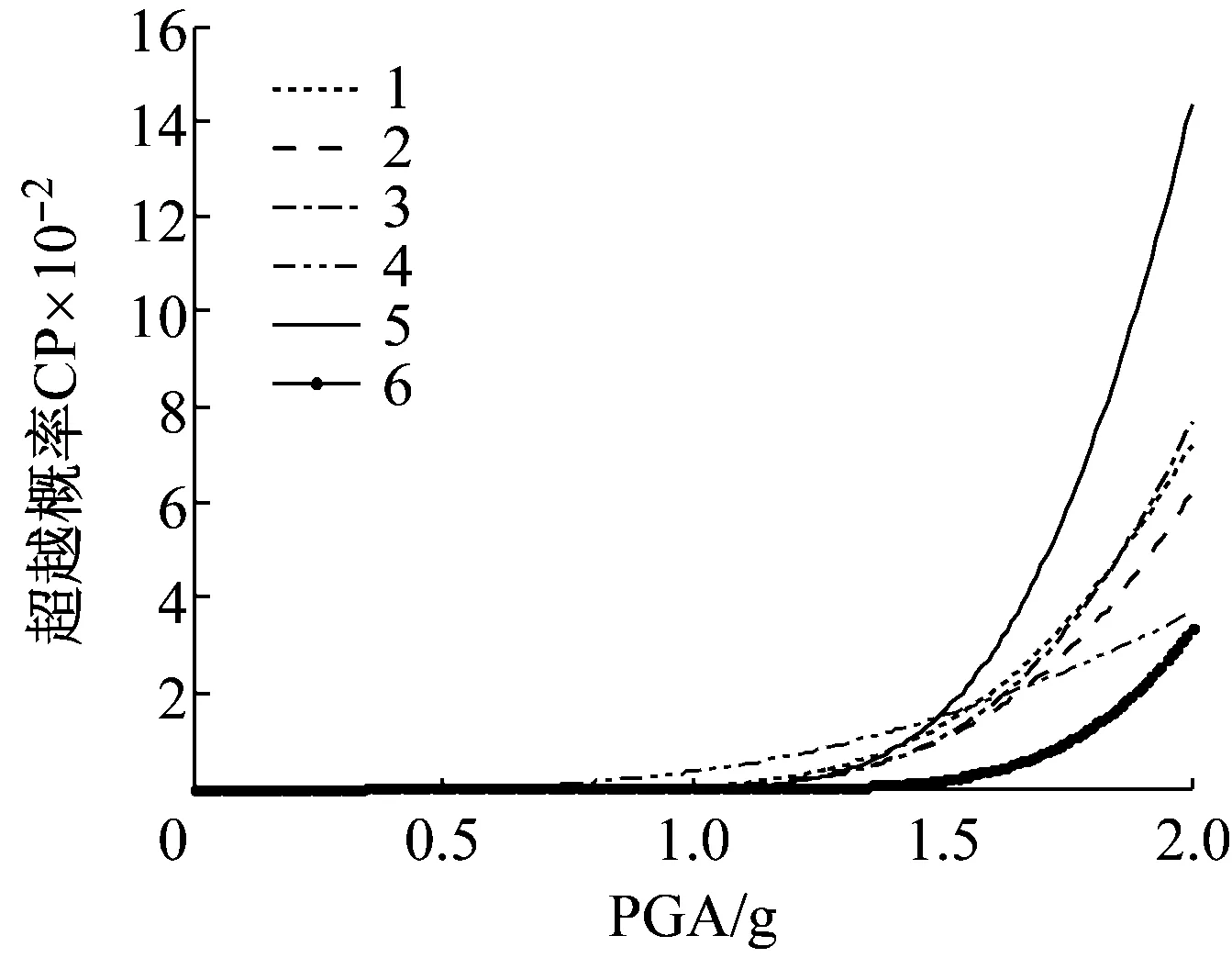
由圖2～圖5可知，當僅布置1個Maxwell阻尼器時，阻尼器的優化布置位置主要取決于結構2的響應，不同的阻尼器布置位置對結構1的超越概率的影響差異較小；應盡量將阻尼器布置在相鄰結構的頂層，這樣可以使兩結構在不同的性能目標下均具有較小的超越概率，并應避免將阻尼器布置在相鄰結構的底層。

(a) 結構

(b) 結構

圖2 IO性能目標下相鄰結構的超越概率曲線(布置1個阻尼器)
Fig.2 Exceeding probability of the adjacent structures under IO performance level (with one damper)

(a) 結構

(b) 結構

圖3 SD性能目標下相鄰結構的超越概率曲線(布置1個阻尼器)
Fig.3 Exceeding probability of the adjacent structures under SD performance level (with one damper)

(a) 結構

(b) 結構

圖4 LS性能目標下相鄰結構的超越概率曲線(布置1個阻尼器)
Fig.4 Exceeding probability of the adjacent structures under LS performance level (with one damper)

(a) 結構

(b) 結構

圖5 CP性能目標下相鄰結構的超越概率曲線(布置1個阻尼器)
Fig.5 Exceeding probability of the adjacent structures under CP performance level (with one damper)

(a) 結構

(b) 結構

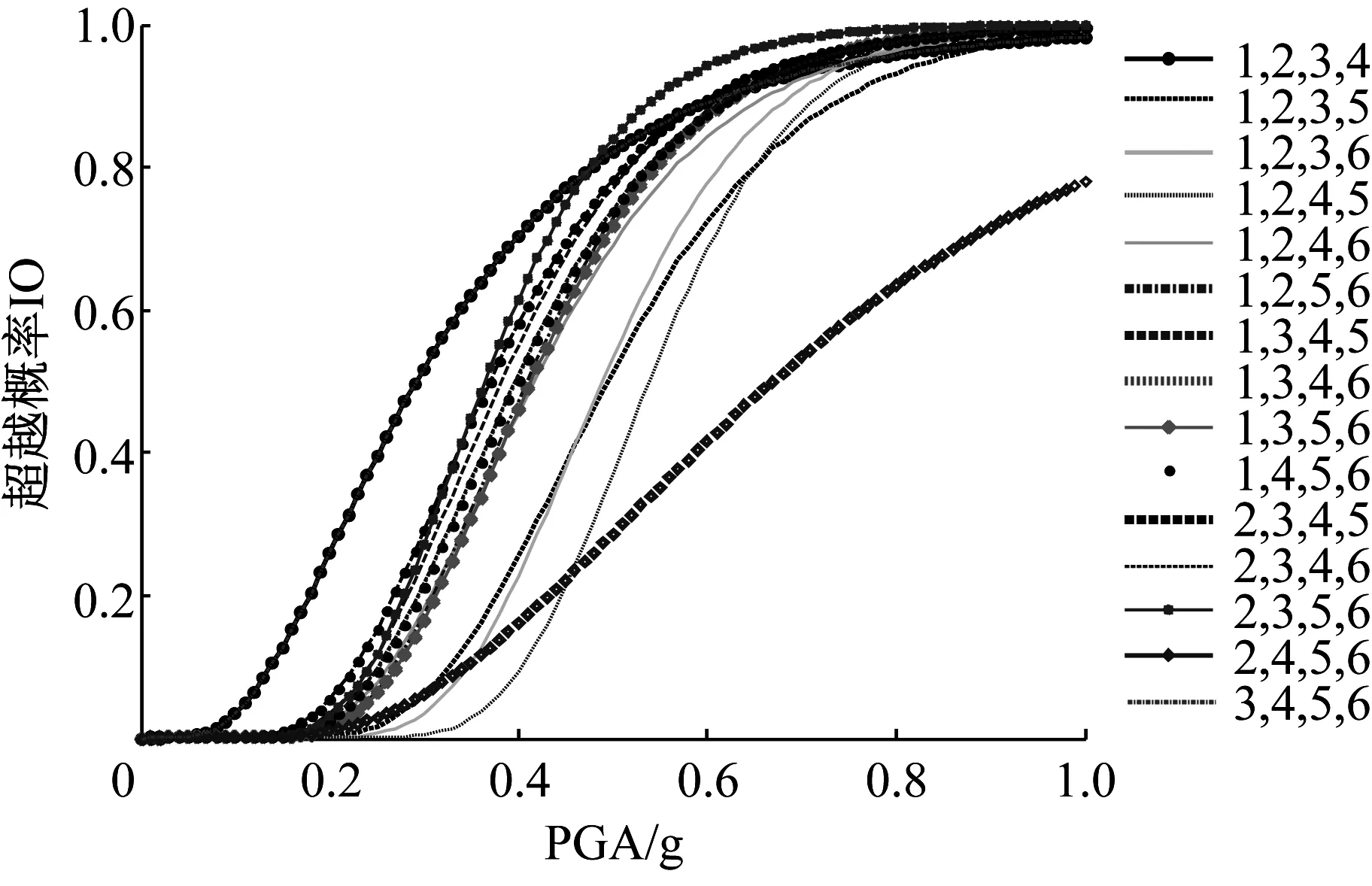
圖6 IO性能目標下相鄰結構的超越概率曲線(布置4個阻尼器)
Fig.6 Exceeding probability of the adjacent structures under IO performance level (with four dampers)

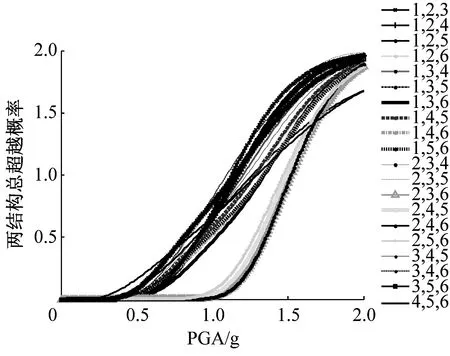
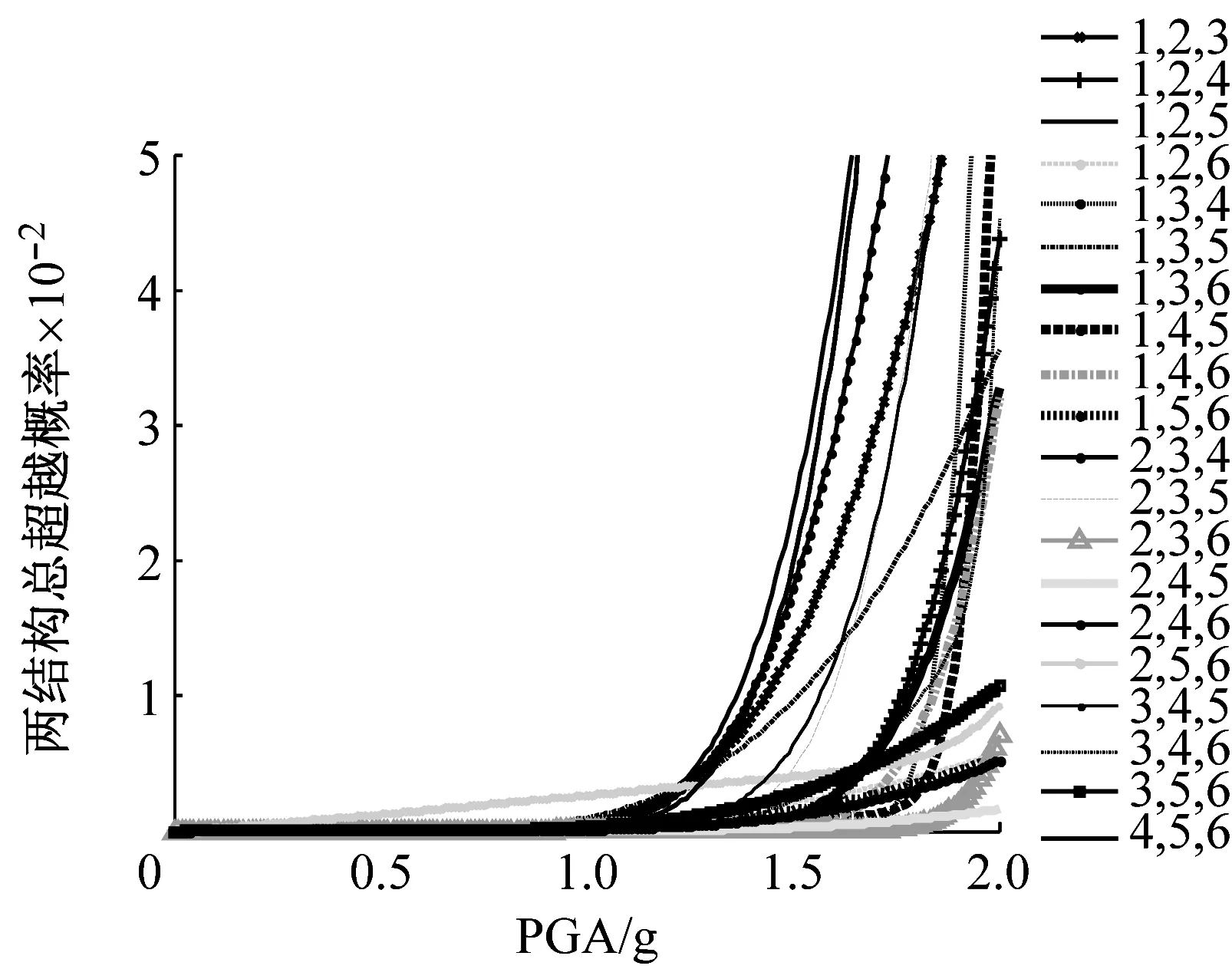
由圖6～圖9可知，當布置4個Maxwell阻尼器時，相鄰結構在不同阻尼器布置位置組合下的超越概率差異較大，這表明進行阻尼器的優化布置是很有必要的。當4個阻尼器分別布置在“1,2,3,5”、“1,2,3,6”、“1,2,4,5”及“2,4,5,6”時，兩結構在不同性能目標下的超越概率明顯小于其它布置組合的情況，尤其是在IO、SD及LS性能目標下，可以將“2,4,5,6”作為阻尼器的最優布置位置；在CP性能目標下可以將“1,2,3,6”作為阻尼器的最優布置位置。應避免將阻尼器集中布置在相鄰結構的某些部位，如IO、SD性能目標中“1,2,3,4”、“3,4,5,6”的阻尼器布置組合下，相鄰結構的超越概率較大；LS、CP性能目標中“2,3,4,5”的阻尼器布置組合下相鄰結構的超越概率較大。因此，無論將阻尼器集中布置在相鄰結構的底部、中部還是頂部，均不能得到較好的控制效果。另外，在“2,3,5,6”布置組合下，兩相鄰結構在各性能目標下的超越概率均較大，尤其是LS、CP性能目標，應避免將阻尼器布置在該位置組合。

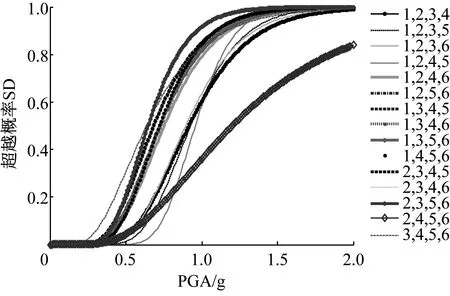
(a) 結構

(b) 結構

圖7 SD性能目標下相鄰結構的超越概率曲線(布置4個阻尼器)
Fig.7 Exceeding probability of the adjacent structures under SD performance level (with four dampers)

由于篇幅有限，本文只給出了布置1個阻尼器和布置4個阻尼器時(分別代表布置較少阻尼器和布置較多阻尼器的情況)相鄰結構在不同性能目標下的超越概率曲線。

(a) 結構

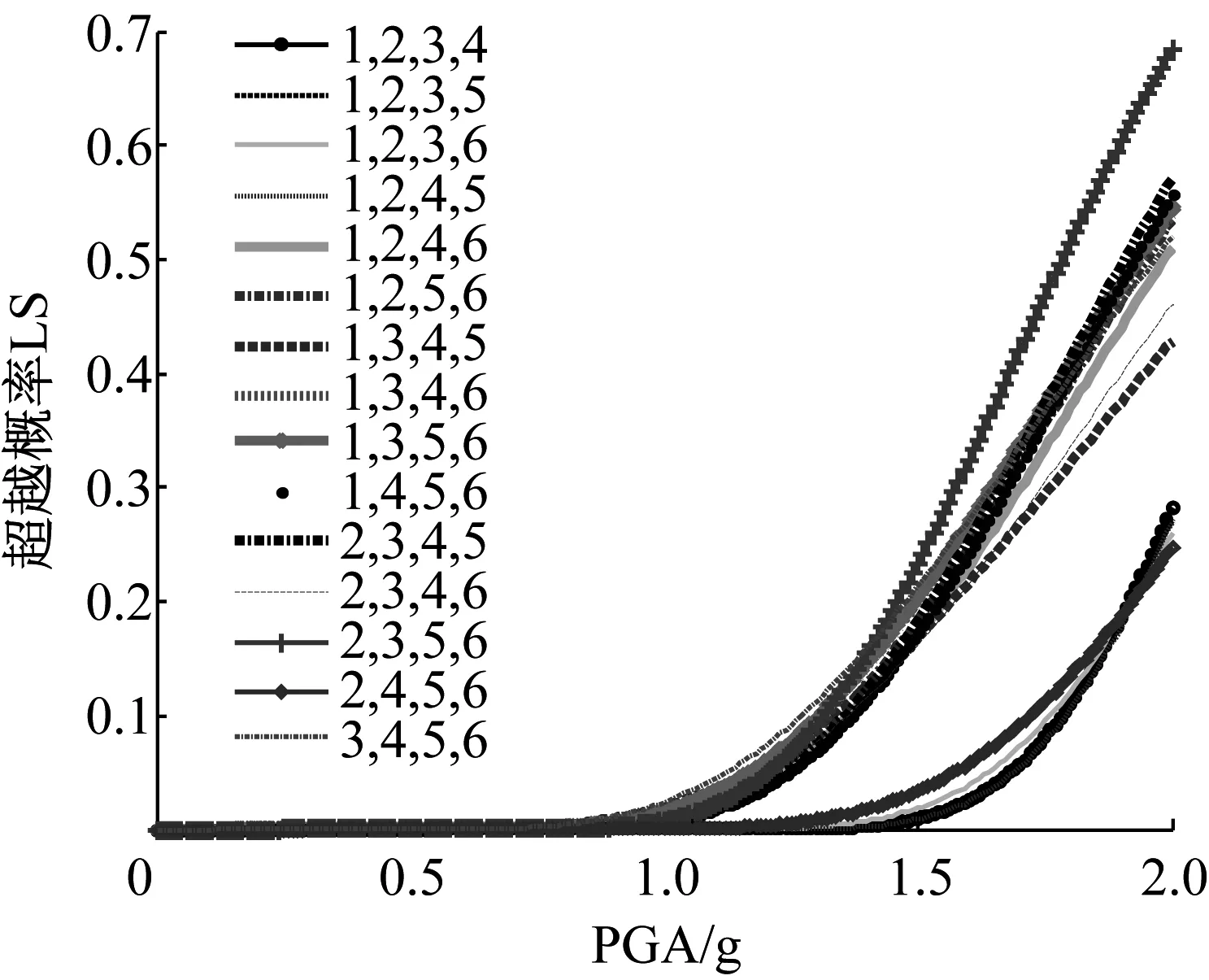
(b) 結構

圖8 LS性能目標下相鄰結構的超越概率曲線(布置4個阻尼器)
Fig.8 Exceeding probability of the adjacent structures under LS performance level (with four dampers)

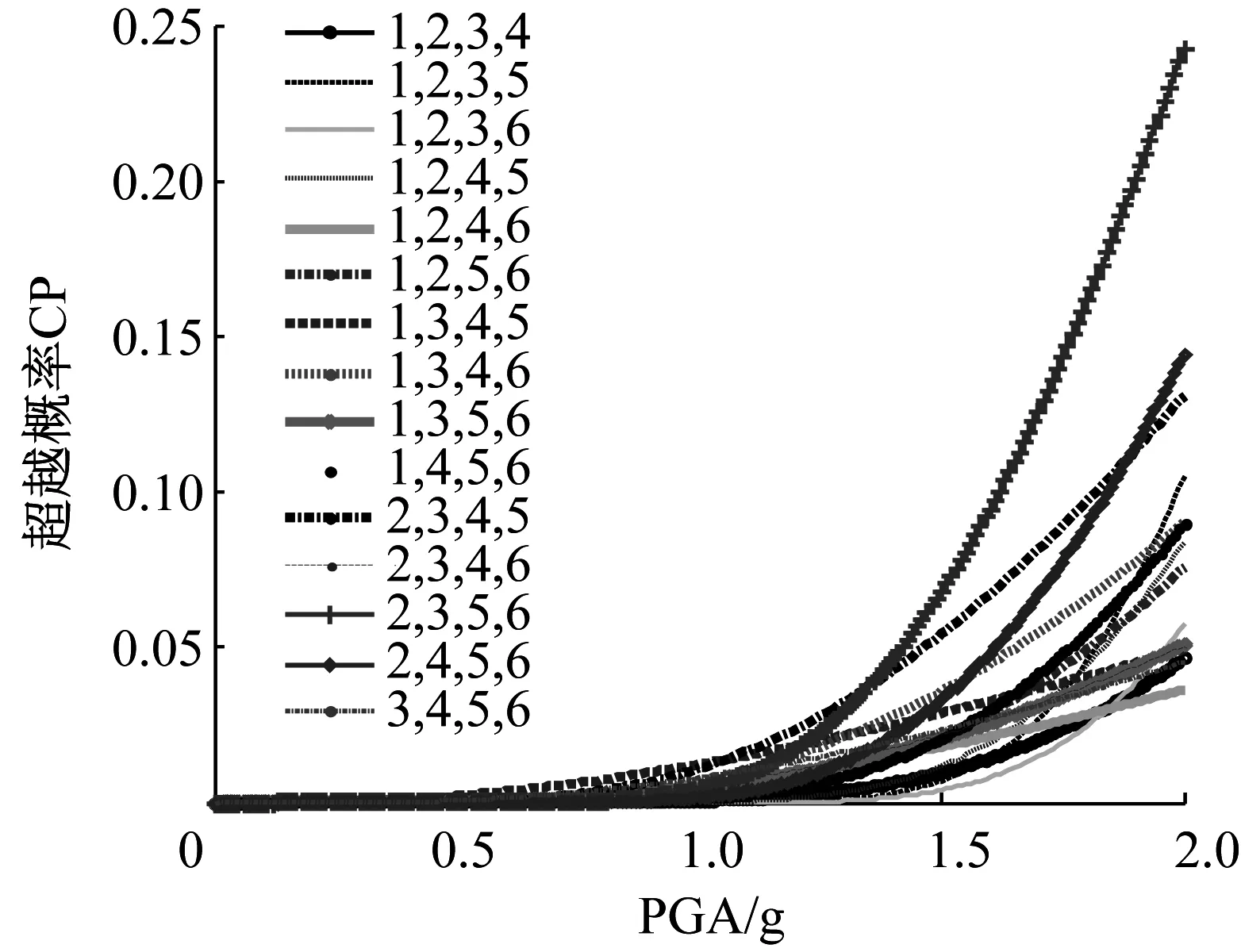
(a) 結構

(b) 結構

圖9 CP性能目標下相鄰結構的超越概率曲線(布置4個阻尼器)
Fig.9 Exceeding probability of the adjacent structures under CP performance level (with four dampers)

3.2.2 不同布置位置組合下相鄰結構的總超越概率

為了給出布置2個、3個及4個阻尼器時，相鄰結構在各性能目標下同時滿足較好控制效果的Maxwell阻尼器優化布置方式，以相鄰結構總超越概率最小為最優控制目標，圖10～圖12給出了不同布置組合下，相鄰結構布置不同阻尼器數目時的總超越概率曲線。

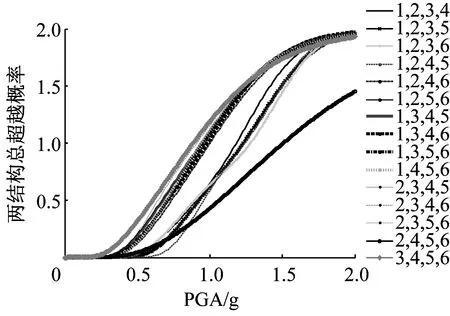
由圖10可知，當在兩結構間布置2個Maxwell阻尼器時，在地震動強度水平較低時(PGA<1.0g)，不同布置組合下，相鄰結構總超越概率差異較小；隨著地震動強度水平的提高，在各性能目標下，“1,6”為最優布置組合，“1,2”為最差布置組合。

由圖11可知，當在兩結構間布置3個Maxwell阻尼器時，在不同性能目標下，相鄰結構在“2,3,6”、“2,4,5”、“2,4,6”、“2,5,6”布置組合下，有明顯低于其它布置組合時的總超越概率。而若在結構某些部位集中布置阻尼器，兩結構的總超越概率較大。

由圖12可知，當在兩結構間布置4個Maxwell阻尼器時，在IO、SD和LS性能目標下，相鄰結構有明顯的最優布置組合即“2,4,5,6”；在CP性能目標下，除“2,3,5,6”布置組合外，相鄰結構在其它布置組合下的總超越概率差別不大。“2,3,5,6”和“3,4,5,6”為較差布置組合形式。

(a) IO

(b) SD

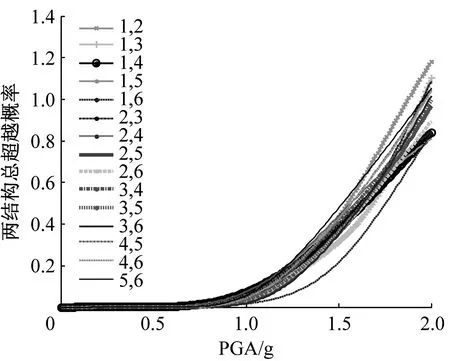
(c) LS

(d) CP

3.2.3 Maxwell阻尼器最優布置位置

以相鄰結構總超越概率最小為優化目標，表2列出了不同布置組合下，相鄰結構在各性能目標下總超越概率的均值，并由此給出了建議的優化布置位置。

由表2可知，不同性能目標下，相鄰結構的最優布置位置的組合不盡相同，為使Maxwell阻尼器對相鄰結構在不同的性能目標下均具有較優控制效果，選取LS或CP性能目標對應的阻尼器最優布置組合，可以實現這一目的。

3.3 Maxwell阻尼器布置數目的優化

將前文建議的Maxwell阻尼器優化布置位置下、相鄰結構在不同性能目標下的總超越概率曲線各繪制在同一圖中，可以更加直觀地比選出Maxwell阻尼器的最優布置數目，如圖13所示。

由圖13可知，當相鄰結構僅布置3個阻尼器時(布置在“2,4,5”)，Maxwell阻尼器在各性能目標下均具有優于其它布置數目下的控制效果。由表2更加可以定量得出，在布置3個阻尼器時，相鄰結構在各性能目標下均具有較小的總超越概率均值。同時，由圖13和表2可知，阻尼器并不是布置的越多越好，當阻尼器滿布時，在各性能目標下，兩結構總的超越概率(均值)幾乎是最大的。

3.4 最優布置驗證

圖14給出了相鄰結構在前文建議的Maxwell阻尼器優化布方式(布置3個阻尼器，且布置在結構的第2層、4層、5層)下的地震易損性曲線，并與未控時的易損性曲線作對比(圖中“-1”表示最優控制；“-2”表示未控)。

由圖14可知，采取最優布置方式布置Maxwell阻尼器的兩結構在各性能水平下的超越概率均遠小于未控時的超越概率，尤其是結構2的控制效果更好：經最優控制后的結構2的超越概率至少可以降低一個性能水平，如經最優控制后的“IO”性能水平的超越概率甚至小于未控時“SD”性能水平的超越概率；經最優控制后的“SD”性能水平的超越概率甚至小于未控時“LS”性能水平的超越概率；經最優控制后的“LS”性能水平的超越概率小于未控時“CP”性能水平的超越概率，證明了本文所提最優布置方案的有效性。

(a) IO

(b) SD

(c) LS

(d) CP

(a) IO

(b) SD

(c) LS

(d) CP

(a) IO

(b) SD

(c) LS

(d) CP

表2 相鄰結構間Maxwell阻尼器的優化布置位置

Tab.2 Results of optimized positions of the Maxwell dampers between the adjacent structures

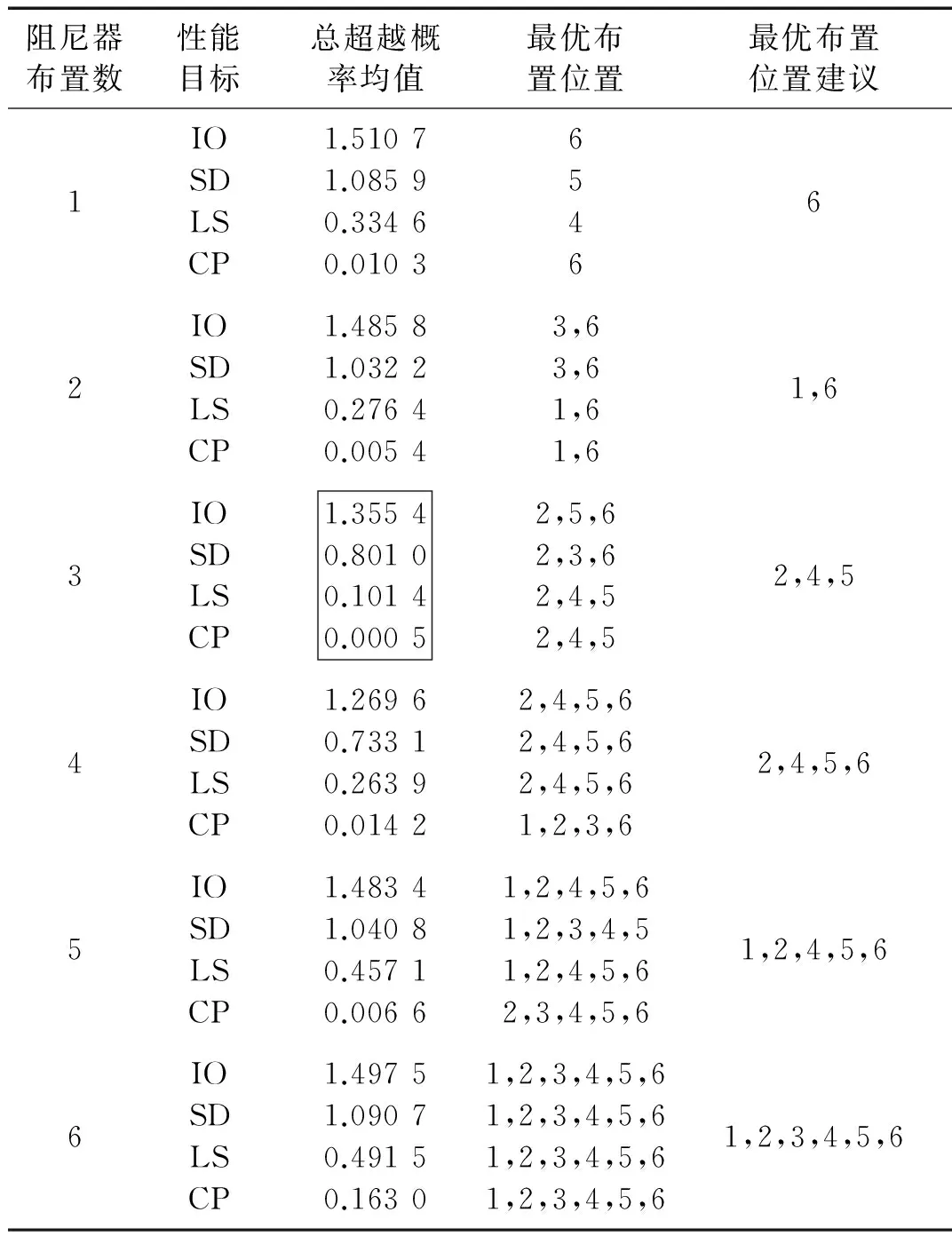
阻尼器布置數性能目標總超越概率均值最優布置位置最優布置位置建議1IOSDLSCP1.51071.08590.33460.0103654662IOSDLSCP1.48581.03220.27640.00543,63,61,61,61,63IOSDLSCP1.35540.80100.10140.00052,5,62,3,62,4,52,4,52,4,54IOSDLSCP1.26960.73310.26390.01422,4,5,62,4,5,62,4,5,61,2,3,62,4,5,65IOSDLSCP1.48341.04080.45710.00661,2,4,5,61,2,3,4,51,2,4,5,62,3,4,5,61,2,4,5,66IOSDLSCP1.49751.09070.49150.16301,2,3,4,5,61,2,3,4,5,61,2,3,4,5,61,2,3,4,5,61,2,3,4,5,6

(a) 結構1

(b) 結構2

4 結 論

本文對地震作用下連接兩相鄰結構的Maxwell阻尼器進行了基于性能的優化布置研究。以兩結構的總超越概率最小為優化控制目標，得出了Maxwell阻尼器在各級性能目標下均具有較好控制效果的最優布置位置和最優布置數目。對于本文算例，通過分析得出以下結論，并為此類阻尼器優化布置位置的選擇提供參考依據：

(1) 相鄰結構間阻尼器布置組合方式越多，進行優化布置的必要性越高，且優化布置的組合形式也越多,反之亦然。

(2) 當相鄰結構間僅布置1個阻尼器時，宜將阻尼器布置在結構頂部，不能布置在結構底部。

(3) 當相鄰結構間僅布置2個阻尼器時，宜將阻尼器分別布置在結構頂部和底部，不能只布置在結構底部。

(4) 當相鄰結構間布置多個阻尼器時，應沿結構高度分別在相鄰結構的底部、中部和頂部均勻布置阻尼器，避免在結構的某個部位集中布置。

(5) 阻尼器并不是布置的越多越好，這樣不僅不經濟，而且在所有布置組合下，阻尼器滿布時，控制效果有時是最差的。

(6) 不同阻尼器布置組合下，相鄰結構地震響應的差異較大，表明進行阻尼器布置位置和布置數目的優化很有必要。

[1] 朱宏平, 俞永敏, 唐家詳. 地震作用下主-從結構的被動優化控制研究[J]. 應用力學學報, 2000, 17(2): 63-69.

ZHU Hongping, YU Yongmin, TANG Jiaxiang. Optimal passive control of primary-auxiliary structures under earthquake excitation[J]. Chinese Journal of Applied Mechanics, 2000, 17(2): 63-69.

[2] 朱宏平, 楊紫健, 唐家祥. 利用連接裝置控制兩相鄰結構的地震響應[J]. 振動工程學報, 2003, 16(1): 57-61.

ZHU Hongping, YANG Zijian, TANG Jiaxiang. Control of the seismic response of two adjacent structures using a damped link[J]. Journal of Vibration Engineering, 2003, 16(1): 57-61.

[3] 朱宏平, 梁露. 兩相鄰結構地震動響應被動優化控制的比較研究[J]. 工程力學, 2005, 22(增刊1): 183-187.

ZHU Hongping, LIANG Lu. Comparative study of passive optimum control for reducing seismic responses of adjacent structures[J]. Engineering Mechanics, 2005, 22(Sup 1): 183-187.

[4] 朱宏平, 翁順, 陳曉強. 控制兩相鄰結構地震動響應的Maxwell模型流體減振器優化參數研究[J]. 應用力學學報, 2006, 23(2): 296-300.

ZHU Hongping, WENG Shun, CHEN Xiaoqiang. Optimum parameters of Maxwell-defined dampers for reducing the seismic responses of adjacent structures under earthquake[J]. Chinese Journal of Applied Mechanics, 2006, 23(2): 296-300.

[5] ZHU H P, XU Y L. Optimum parameters of Maxwell model-defined dampers used to link adjacent structures[J]. Journal of Sound and Vibration, 2005, 279(1/2): 253-274.

[6] ZHU H P, GE D D, HUANG X. Optimum connecting dampers to reduce the seismic responses of parallel structures[J]. Journal of Sound and Vibration, 2011, 330(9): 1931-1949.

[7] ZHANG W S, XU Y L. Vibration analysis of two buildings linked by Maxwell model-defined fluid dampers[J]. Journal of Sound and Vibration, 2000, 233(5): 775-796.

[8] BHASKARARAO A V, JANGID R S. Optimum viscous damper for connecting adjacent SDOF structures for harmonic and stationary white noise random excitations[J]. Earthquake Engineering and Structural Dynamics, 2007, 36(4): 563-571.

[9] QUINONERO P F, MASSEGU J R, ROSSELL J M, et al. Vibration control for adjacent structures using local state information[J]. Mechatronics, 2014, 24: 336-344.

[10] PARK K S, OK S Y. Hybrid control approach for seismic coupling of two similar adjacent structures[J]. Journal of Sound and Vibration, 2015, 349: 1-17.

[11] 易凌, 吳從曉. 黏滯阻尼器連接的相鄰隔震與非隔震建筑地震反應分析[J]. 工程抗震與加固改造, 2012, 34(4): 61-72.

YI Ling, WU Congxiao. Seismic response analysis of linking viscous dampers connecting base-isolated structure with adjacent building[J]. Earthquake Resistant Engineering and Retrofitting, 2012, 34(4): 61-72.

[12] 閤東東. 利用主從結構相互作用的被動控制研究[D]. 武漢：華中科技大學，2010.

[13] 吳巧云, 朱宏平, 陳楚龍. 連接Maxwell模型的兩相鄰結構地震易損性分析[J]. 振動與沖擊, 2015, 34(21): 171-178.

WU Qiaoyun, ZHU Hongping, CHEN Chulong. Seismic fragility analysis of two adjacent structures connected with Maxwell dampers[J]. Journal of Vibration and Shock, 2015, 34(21): 171-178.

[14] SHOME N, CORNELL C A. Probabilistic seismic demand analysis of nonlinear structures: RMS-35[R]. Stanford: Stanford University, 2004.

[15] 吳巧云, 朱宏平, 樊劍. 基于性能的鋼筋混凝土框架結構地震易損性分析[J]. 工程力學, 2012, 29(9): 117-124.

WU Qiaoyun, ZHU Hongping, FAN Jian. Performance-based seismic fragility analysis of RC frame structures[J]. Engineering Mechanics, 2012, 29(9): 117-124.

[16] 建筑抗震設計規范:GB 5011—2010[S]. 北京: 中國建筑工業出版社, 2010.

Performance-based optimal arrangement of Maxwell dampers between two adjacent structures

WU Qiaoyun1,2, ZHU Hongping2, CHEN Xuyong1,2

(1. School of Resource and Civil Engineering, Wuhan Institute of Technology, Wuhan 430073, China;2. School of Civil Engineering and Mechanics, Huazhong University of Science and Technology, Wuhan 430074, China)

Performance-based optimal arrangement of Maxwell dampers between two adjacent reinforced concrete frame structures was studied. The minimum total exceeding probability of two adjacent structures was taken as the optimization objective. The optimal arranging positions of Maxwell dampers between two adjacent structures under the conditions of some certain numbers of dampers were firstly studied. The general arranging laws for optimal positions of Maxwell dampers between two adjacent structures were obtained. Through the seismic fragility analyses of two adjacent structures connected using Maxwell dampers with different optimal arranging positions, the optimal numbers of Maxwell dampers used to connect two adjacent structures were determined. The results showed that the proposed optimal arrangements of Maxwell dampers between two adjacent structures has better control effects for two adjacent structures under earthquakes with different performance targets; the results provide a helpful reference for further engineering applications.

adjacent structures; Maxwell damper; optimum position; optimum number; seismic fragility; exceeding probability

國家自然科學基金資助項目(51408443)；湖北省教育廳科研項目(Q20141503)；中國博士后科學基金資助項目(2013M542024)

2015-08-05 修改稿收到日期：2016-01-22

吳巧云 女，博士后，副教授，1985年生

朱宏平 男，博士，教授，博士生導師，1965年生

TU311.3; TU375.4

A

10.13465/j.cnki.jvs.2017.09.006