L∞范數擬合正則化方法在飛行器動態載荷識別中的應用
高 偉, 于開平, 蓋曉男
(哈爾濱工業大學 航天學院,哈爾濱 150001)
L∞范數擬合正則化方法在飛行器動態載荷識別中的應用
高 偉, 于開平, 蓋曉男
(哈爾濱工業大學 航天學院,哈爾濱 150001)
基于變限積分理論,構造了響應函數最小二乘意義下的加權變限積分。通過適當次數的積分滑動平均,有效過濾測量噪聲中的高頻噪聲。針對測量響應中殘留的低頻噪聲,使用L∞范數擬合正則化方法識別載荷,提出了一種選取L∞范數擬合正則化方法最優正則化參數的單調性檢驗方法。數值仿真及試驗驗證說明單調性檢驗方法可以有效確定L∞范數擬合正則化方法的最優正則化參數,得到比傳統L2范數正則化方法擬合性質更好精度更高的識別載荷;針對遙測數據中噪聲特點,使用模擬遙測數據利用L∞范數擬合正則化方法對沖擊載荷進行了有效識別。
載荷識別;L∞范數正則化方法;滑動平均;遙測數據
載荷識別問題和系統辨識問題是反問題理論中的兩類問題[1-2]。很多實際工程問題中,直接測量工程結構所受動態載荷非常困難甚至是不可能的,比如火箭點火和分離時飛行器結構所受沖擊載荷、導彈在發射和飛行時某些關鍵部位的動態載荷信息等。飛行器關鍵部位所受動態載荷信息在飛行器模態分析、內力識別、強度校核等領域扮演關鍵角色。所以載荷識別技術越來越受到人們的重視,載荷識別技術是在結構響應及系統模型已知的情況下識別外部動態載荷[3-5]。載荷識別問題往往是不適定的,伴隨正則化方法[6]的提出大量專家投入到載荷識別技術的研究中來。
目前,載荷識別技術主要有頻域和時域兩類[7]。載荷識別頻域方法發展較早,基本思想是在頻域內建立輸入、系統、輸出三者之間的系統模型。頻域方法載荷識別系統模型的建立及求解相對容易,對于周期形式的載荷可以得到較好的識別結果。但是頻域方法也存在自身的局限性,比如在共振頻率附近頻響函數矩陣呈現病態。另外,頻域方法還要求結構響應數據具有一定的長度以便得到高精度的頻譜,所以頻域方法對于瞬態脈沖載荷的識別具有較大的局限性。與頻域方法相比較,載荷識別時域方法對數據長度并無要求,所以時域方法更適用于瞬態脈沖載荷識別問題。Doyle[8]提出的小波反卷積方法識別的沖擊載荷比頻域方法識別結果有更高的精度。載荷識別頻域方法得到的結果為關心頻帶內的載荷譜。而時域方法得到的結果是更加直觀的時域內的載荷時間歷程,所以載荷識別時域方法更容易研究載荷在時域內的表現形式。載荷識別時域方法中,正則化方法是目前使用最普遍的載荷識別方法。Sanchez等[9]總結了一些目前得到充分研究及成功用于載荷識別的L2范數正則化方法,指出系統矩陣的病態性及測量噪聲是引起載荷識別誤差的主要因素。L2范數是高斯白噪聲的最佳最小二乘近似,所以傳統L2范數正則化方法針對高斯白噪聲可以得到理想的載荷識別結果[10]。但是在實際工程應用中存在高斯白噪聲水平較高的情況,積分滑動平均可以有效抑制高水平高斯白噪聲中的高頻噪聲部分,殘留的低水平噪聲部分不再是白噪聲,而是較小幅值的低頻形式的噪聲。另外,在飛行器關鍵部位動態載荷識別所使用的遙測數據采集過程中,由于環境噪聲及數據采集系統噪聲的影響,遙測數據中的噪聲不具有高斯白噪聲特性,而是近似服從均勻分布的隨機噪聲。前面提到的較小幅值的低頻形式噪聲及遙測數據中近似服從均勻分布的隨機噪聲,不是L2范數正則化方法的最佳適用噪聲形式。L∞范數是均勻噪聲的最佳最小二乘近似,Clason[11]提出的L∞范數擬合正則化方法針對均勻噪聲可以得到理想的載荷識別結果,所以本文引入L∞范數擬合正則化方法進行飛行器動態載荷識別并與傳統L2范數正則化方法載荷識別結果相比較。
本文主要研究L∞范數擬合正則化方法在實際工程載荷識別問題中的應用。下文組織如下。第1部分建立用于載荷識別的離散系統方程積分滑動平均模型。第2部分介紹了L∞范數擬合正則化方法;第3部分基于最優化問題的目標函數,提出了用于確定L∞范數擬合正則化方法最優正則化參數的單調性檢驗方法。第4部分通過數值仿真算例及試驗驗證說明了L∞范數擬合正則化方法及單調性檢驗方法的合理性及有效性,并且給出了與L2范數正則化方法的比較結果。第5部分中給出使用新方法基于模擬遙測數據對加載在飛行器結構上關鍵部位沖擊載荷的無量綱化識別結果。最后在第6部分中給出結論。
1 離散系統方程模型
載荷識別離散系統方程模型的建立方法之一是基于Duhamel積分的離散化。

(1)

(2)
式中,n=1,2,…為積分次數。適當進行多次積分以后可以得到方程為
(3)

(4)
再令
(5)
則由(5)式中矩陣可逆有
(6)
由式(6)可得權函數為
hk(t)=u[t+(m-k)Δt]
(7)
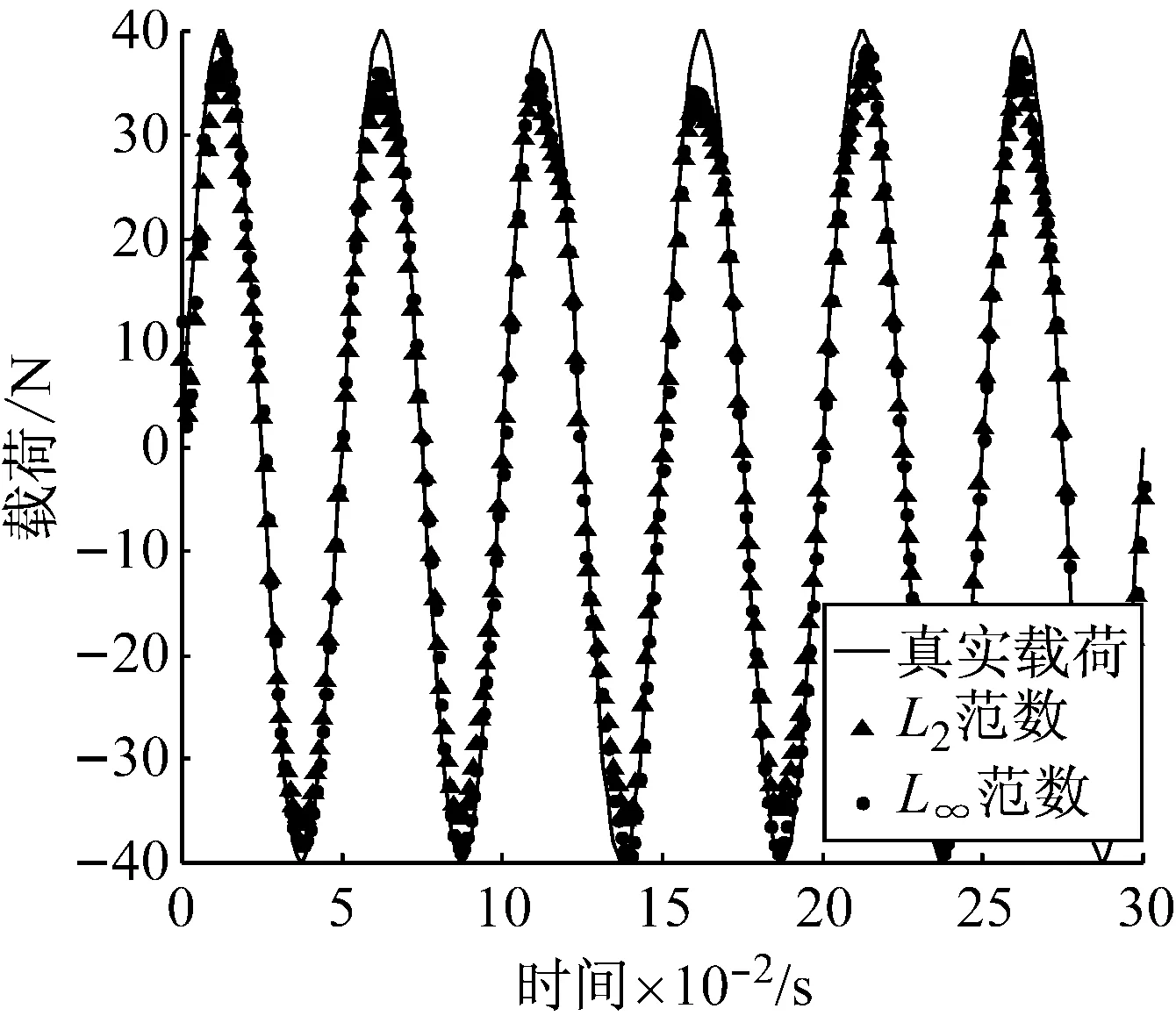
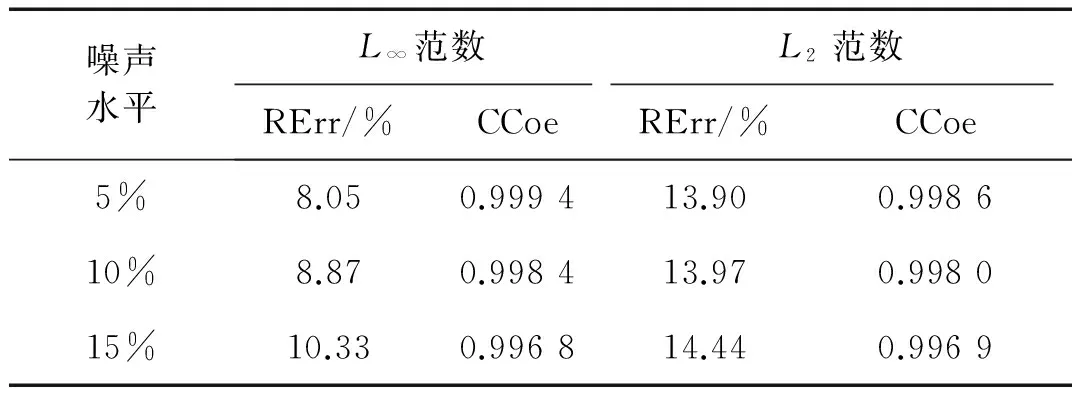
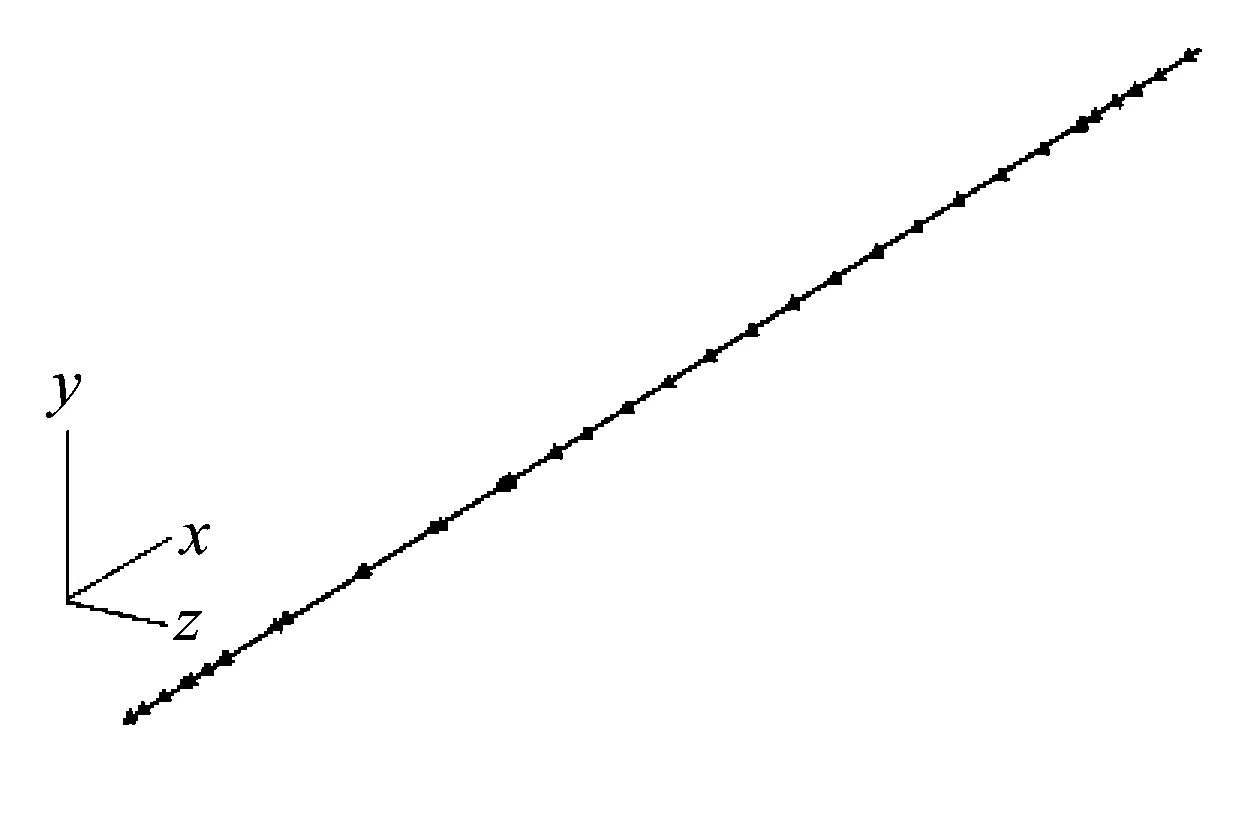
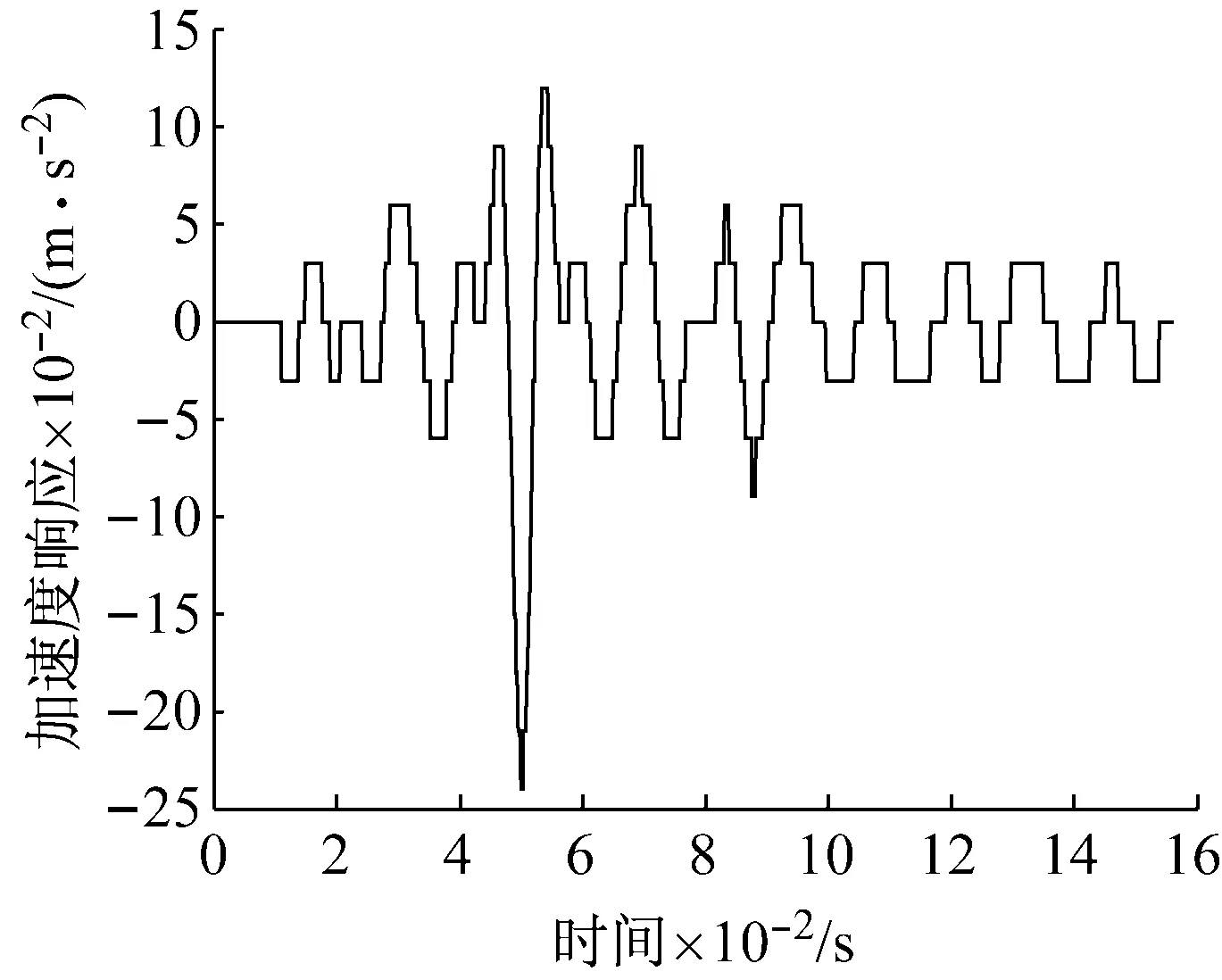
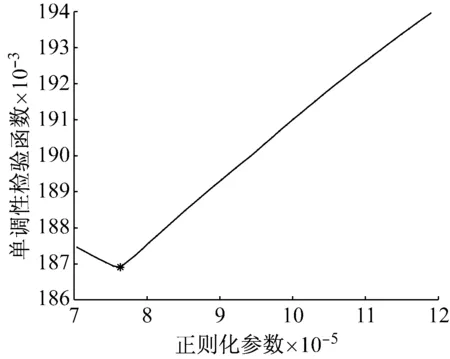
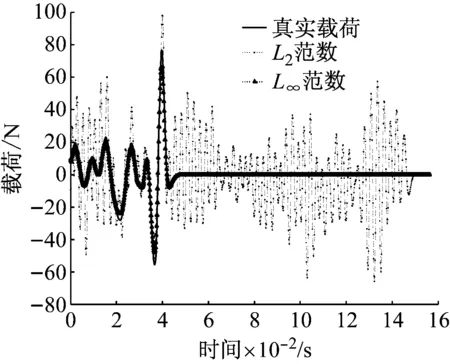
式中:4≤k≤Q-2;(k-1)Δt (8) 同理有 (9) 再利用最小二乘擬合形函數方法[13],基于前面整個時間域的離散化方式可得離散系統方程為yn=Gp,再由5.2次平滑系數令矩陣M為 (10) 由式(9)及式(10)有 yn=Myn-1=…=Mny* (11) 式中,y*=[y*(t1),y*(t2),…,y*(tQ)]T。取定合適的積分次數n=n0,則有離散系統方程模型 Mn0y*=Gp (12) 針對式(12)中離散系統方程,L∞范數正則化方法考察最優化問題 (13) (14) 式中,c∈R為一實數。約束條件中L∞范數是不可導的,所以利用Moreau-Yosida近似來解決這個問題。對于γ>0,式(14)的Moreau-Yosida近似為 (15) 式中,max,min兩個函數均為逐點運算。式(15)中Moreau-Yosida近似所考察最優化問題的解強收斂到式(14)中所考察的最優化問題的解。式 (15)中最優化問題目標函數為嚴格凸及弱下半連續。由式(15)中最優化問題的目標函數可導,可以使用半光滑牛頓法求解式(15)中最優化問題[15-16]。 由式(13)中最優化問題目標函數,我們定義函數為 (16) (2) 當α*≈α時,式(13)中擬合項與正則項處于較好的折中狀態,所以在參數α*附近非常小的范圍內,函數H(α)的值幾乎不變。 (4) 所以我們選定最優正則化參數值αop滿足H(αop)=minH(α)。 單調性檢驗方法算法實現 步驟1 由系統矩陣G的SVD (Singular Value Decomposition)[17]分解得系統矩陣最大奇異值σ1,給出初始參考向量α=[σ1/50, 2σ1/50, …,σ1]。 步驟2 計算H(α)函數值構成的向量H=[H(α1),H(α2),…,H(α50)]。 步驟3 如果H中的最小分量恰為第一個分量,更新參數向量為α1=α/2。 步驟4 重復步驟2、步驟3直到向量H中的第一個分量不再是最小分量(假設此時H中的最小分量為第j個分量,其中2 采用懸臂梁有限元模型用來模擬將在試驗驗證中使用的圖7所示真實鋼制懸臂梁結構。將此懸臂梁劃分為10個單元,10個節點從左到右依次編號1-10。假設懸臂梁結構所對應系統為線性系統,且在載荷加載到結構上之前初始條件為0,如圖1所示。 圖1 懸臂梁有限元模型 另外用于載荷識別的加速度響應數據假設受到環境測量噪聲的污染,所以建立給數值計算的加速度響應中添加噪聲的公式模型為 y*=ytrue+lnonoisestd(ytrue) (17) 式中:y*為用于載荷識別的加速度響應;ytrue為數值計算得到的響應;lno為噪聲水平;noise為均值為0方差為1的白噪聲序列;std(ytrue)為真實響應ytrue的標準差。識別載荷與真實載荷之間的相對誤差及相關系數計算公式為 (18) (19) 圖2 積分滑動平均后殘留低頻噪聲 在數值仿真算例中取基函數向量為q(t)=[1,t,t2]T構造式(12)中離散系統方程,使用L∞范數擬合正則化方法和L2范數正則化方法進行載荷識別,分別使用單調性檢驗和GCV (Generalized Cross-Validation)方法來確定最優正則化參數,最后將兩種正則化方法所得載荷識別結果進行比較分析。 4.1 正弦載荷識別 在第8節點處施加正弦載荷p1(t)=40sin(40πt),載荷作用時間為0.3 s。采樣頻率為1 000 Hz,使用第4節點處的加速度響應分別在5%、10%及15%噪聲水平下進行載荷識別,積分滑動平均次數為30。15%噪聲水平下,函數H(α)圖像,如圖3所示,圖3中星號處表示最優正則化參數所在位置。兩種正則化方法所得識別載荷,如圖4所示。不同噪聲水平下正弦載荷識別相關結果見表1。由圖4可知,在正弦載荷識別過程中,單調性檢驗方法及GCV方法均可以有效確定兩種正則化方法的最優正則化參數,相應識別載荷較好的反映了真實載荷的時間歷程。另外,不難看出在正弦載荷的峰值附近L∞范數擬合正則化方法所得識別載荷與真實載荷有更好的擬合性質。 圖3 15%噪聲水平下函數H(α) 圖4 15%噪聲水平下識別正弦載荷 表1 正弦載荷識別結果 Tab.1 Results of the identified sinusoidal load 噪聲水平L∞范數L2范數RErr/%CCoeRErr/%CCoe5%8.050.999413.900.998610%8.870.998413.970.998015%10.330.996814.440.9969 4.2 沖擊載荷識別 半正弦波可以用來表示典型的沖擊載荷[18],所以在第8節點處施加沖擊載荷 (20) 整個時間歷程為0.03 s。采樣頻率為5 000 Hz,使用第6節點處長度為0.03 s的加速度響應,分別在5%,10%及15%噪聲水平下識別沖擊載荷,積分滑動平均次數為30。沖擊載荷的主要特征為最大幅值[19],所以文中沖擊載荷對應的RErr指的是識別載荷最大幅值與真實載荷最大幅值之間的RErr。 5%噪聲水平下兩種正則化方法所得識別載荷,如圖5所示。不同噪聲水平下對沖擊載荷識別相關結果見表2。由圖5可知,L∞范數擬合正則化方法所得識別載荷較好的反映了沖擊載荷的時間歷程,與真實載荷有較好的擬合性質,識別載荷最大幅值與真實沖擊載荷最大幅值非常接近。L2范數擬合正則化方法對應的識別載荷最大幅值與真實幅值差別相對較大。相關識別結果見表2。經計算真實沖擊載荷最大幅值為39.92。 圖5 5%噪聲水平下識別沖擊載荷 表2 沖擊載荷識別結果 Tab.2 Results of the identified impact load 噪聲水平5%10%15%L∞范數L2范數幅值39.2539.1639.04RErr/%1.671.912.20幅值38.1738.1338.09RErr/%4.394.494.58 綜合數值仿真中使用兩種不同正則化方法針對不同形式載荷的識別結果可得,單調性檢驗方法能夠有效確定L∞范數擬合正則化方法的最優正則化參數,得到理想精度的穩定數值解。利用積分滑動平均有效抑制白噪聲中的高頻噪聲部分,對于殘留的低頻噪聲部分L∞范數擬合正則化方法與L2范數擬合正則化方法相比較有更好的適應性,L∞范數擬合正則化方法能夠得到精度更高光滑性質更好的識別載荷。同時也說明與L2范數正則化方法相比較,L∞范數擬合正則化方法對于結構響應中的測量噪聲有更好的穩定性。 圖6 不同模型誤差下載荷識別結果 由式(12)中離散系統方程模型中系統矩陣G是通過有限元方法計算的形函數響應所構造,形函數響應中可能會包含結構有限元模型建立過程中所帶來的模型誤差。因此,考察兩種正則化方法對于模型誤差的穩定性是非常重要的。初始條件保持不變,模型誤差添加公式為Gerror=G(1+Δ),其中Δ表示模型誤差水平[20]。結果如圖6所示,如果以沖擊載荷識別誤差在10%以內為滿足我們需要的標準,則當模型誤差在7%以內時L2范數正則化方法可以得到理想的載荷識別結果,而L∞范數擬合正則化方法對于10%以內的模型誤差均可以得到理想的沖擊載荷識別結果。圖6中結果說明L∞范數擬合正則化方法對于模型誤差有比L2范數正則化方法更好的穩定性。 4.3 試驗驗證 懸臂梁結構實驗圖片如圖7所示,基本假設及初始條件與數值模擬中相同。懸臂梁左端固定右端自由。規格0.9 m×0.05 m×0.009 m,密度7.8×103kg/m3,彈性模量E=200 Gpa。將此懸臂梁劃分為10個單元,如圖1所示,從左到右依次為節點1~10。在第8節點處施加頻率為20 Hz的正弦形式載荷并同時測量真實載荷數據,載荷作用時間為0.5 s,在第3~第6節點處放置加速度傳感器測量結構響應,采樣頻率為1 024 Hz。 圖7 懸臂梁結構 使用第6節點處加速度響應識別載荷,如圖8所示。L∞范數正則化方法識別載荷RErr及CCoe分別為 圖8 試驗驗證識別載荷 17.46%及0.986 2。L2范數正則化方法識別載荷RErr及CCoe分別為17.51%及0.986 0。識別載荷初始時刻附近的波動原因為載荷的突然加載產生的瞬態脈沖響應造成的干擾。實驗室環境下,環境帶來的測量噪聲及數據采集系統噪聲都處于非常低的水平,所以使用兩種正則化方法進行載荷識別所得結果的誤差及精度幾乎沒有差別。 飛行器結構在點火、分離瞬間關鍵部位所受沖擊載荷可能導致飛行器結構嚴重損傷,所以飛行器結構沖擊載荷識別問題是一類典型的非常重要的載荷識別問題。建立飛行器的三維集中質量梁模型,如圖9所示,集中質量三維梁模型共34個質量站點,建立34個0D單元屬性,mass_1到mass_34,分別賦給相對應的站點建立34個point單元。按照給定的艙段劃分,再建立12個1D單元屬性,liang_1~liang_7及liang_9~liang_13分別賦給相對應的艙段建立33個bar單元。構造形如圖13中實線所代表的模擬沖擊載荷,用此模擬沖擊載荷來模擬飛行器級間分離時刻結構y方向所受典型沖擊載荷。將模擬沖擊載荷作用于飛行器級間分離位置所對應的質量站點,使用飛行器模擬遙測加速度響應來識別模擬沖擊載荷。 圖9 集中質量梁模型 遙測數據采集過程中,由于數據采集系統精度的限制導致采集到的響應數據只能分布在一些特定的數值上,如圖10所示。所以遙測數據中所包含的噪聲主要來源就是數據采集系統帶來的系統噪聲。由于受到環境噪聲及采集系統噪聲的綜合影響,導致遙測數據中所包含的噪聲并不是高斯白噪聲,而是一種水平較高的近似服從均勻分布的隨機噪聲,如圖11中概率密度分布所示。實際情況中飛行器載荷識別問題所使用的響應數據是遙測數據。既往的飛行器沖擊載荷識別問題研究中所考慮的噪聲基本為高斯白噪聲,鮮有考慮噪聲為均勻分布或者近似服從均勻分布情況下的飛行器沖擊載荷識別問題研究。由Clason提出的L∞范數擬合正則化方法適用與均勻分布的噪聲情形,所以我們使用L∞范數擬合正則化方法及模擬遙測數據進行載荷識別。模擬遙測數據采樣頻率為6 400 Hz,類似數值仿真算例中方法計算形函數響應。使用第17質量站點處y方向的形函數響應及模擬遙測數據構造形如式(12)中離散系統方程。 圖10 模擬遙測數據 圖11 系統噪聲概率密度分布 這里由于系統噪聲并非高斯白噪聲,而是水平較高的近似服從均勻分布的隨機噪聲。對于此種噪聲積分滑動平均并不能有效的抑制噪聲,所以取積分滑動平均次數n0=0,也即不對模擬遙測數據進行積分滑動平均。分別用兩種正則化方法進行載荷識別。單調性檢驗函數H(α)圖像,如圖12所示,圖12中星號代表最優正則化參數所在位置。兩種正則化方法識別模擬沖擊載荷,如圖13所示,L∞范數擬合正則化方法識別沖擊載荷在兩處最高峰值處的相對誤差由左至右分別為9.9%和10.4%。L2范數正則化方法識別結果不理想,說明對于此種近似均勻分布噪聲L2范數正則化方法并不適用。L∞范數擬合正則化方法可以有效識別動態載荷,所以與L2范數擬合正則化方法相比較L∞范數擬合正則化方法對于噪聲形式有更大的適用范圍。 圖12 沖擊載荷識別單調性檢驗函數H(α) 圖13 識別模擬沖擊載荷 在飛行器動態載荷識別問題中,針對較高水平高斯白噪聲情形下載荷識別問題,L∞范數擬合正則化方法結合積分滑動平均可以有效識別動態載荷。針對遙測數據中主要由數據采集系統帶來的近似服從均勻分布的較高水平系統噪聲,L2范數擬合正則化方法具有自身的局限性。然而,L∞范數擬合正則化方法可以有效識別沖擊載荷并得到擬合性質較好精度較高的識別結果,所以與L2范數擬合正則化方法相比較L∞范數擬合正則化方法對于結構響應中的測量噪聲有更好的適用范圍及穩定性。與L2范數擬合正則化方法相比較,L∞范數擬合正則化方法同樣對于系統模型誤差有更好的穩定性。因此,綜合數值模擬及試驗驗證中動態載荷識別結果,與L2范數擬合正則化方法相比較L∞范數擬合正則化方法具有更大的適用范圍及更好的穩定性。 [1] 郭榮, 房懷慶, 裘剡, 等. 基于Tikhonov正則化及奇異值分解的載荷識別方法[J]. 振動與沖擊, 2014, 33(6): 53-58. GUO Rong, FANG Huaiqing, QIU Shan, et al. Novel load identification method based on the combination of Tikhonov regularization and singular value decomposition[J]. Journal of Vibration and Shock, 2014, 33(6): 53-58. [2] 楊武, 劉莉, 周思達, 等. 前后向時間序列模型聯合估計的時變結構模態參數辨識[J]. 振動與沖擊, 2015, 34(3):129-135. YANG Wu, LIU Li, ZHOU Sida, et al. Modal parameter identification of time-varying structures using a forward-backward time series model based on joint estimation[J]. Journal of Vibration and Shock, 2015, 34(3):129-135. [3] 馬超, 華紅星. 基于改進正則化方法的狀態空間載荷識別技術[J]. 振動與沖擊, 2015, 34(11): 146-149. MA Chao, HUA Hongxing. State space load identification technique based on an improved regularized method[J]. Journal of Vibration and Shock, 2015, 34(11): 146-149. [4] GHAJARI M, SHARIF-KHODAEI Z, ALIABADIL M H, et al. Identification of impact force for smart composite stiffened panels[J]. Smart Materials and Structures, 2013, 22(8): 085014-085026. [5] 馬超, 華紅星. 一種基于新的正則化技術的沖擊載荷識別方法[J]. 振動與沖擊, 2015, 34(12): 164-168. MA Chao, HUA Hongxing. Impact force identification based on improved regularization technique[J]. Journal of Vibration and Shock, 2015, 34(12): 164-168. [6] INNOUE H, HARRIGAN J J, REID S R. Review of inverse analysis for indirect measurement of impact force[J]. Applied Mechanics Reviews, 2001, 54(6): 503-524. [7] THITE A N, THOMPSON D J. The quantification of structure-borne transmission paths by inverse methods, Part1: improved singular value rejection methods[J]. Journal of Sound and Vibration, 2003, 264(2): 411-431. [8] DOYLE J F. A wavelet deconvolution method for impact force identification[J]. Experimental Mechanics, 1997, 37(4): 403-408. [9] SANCHEZ J, BENAROYA H. Review of force reconstruction techniques[J]. Journal of Sound and Vibration, 2014, 333(14): 2999-3018. [10] MAO Y M, GUO X L, ZHAO Y. A state space force identification method based on Markov parameters precise computation and regularization technique[J]. Journal of Sound and Vibration, 2010, 329(15): 3008-3019. [11] CLASON C.L∞fitting for inverse problems with uniform noise[J]. Inverse Problem, 2012, 28(10): 104007. [12] GORRY P A. General least-squares smoothing and differentiation by the convolution (savitzky-golay) method[J]. Analytical Chemistry, 1990, 62(6): 570-573. [13] LIU J, SUN X S, HAN X, et al. A novel computational inverse technique for load identification using the shape function method of moving least square fitting[J]. Computers and Structures, 2014, 144: 127-137. [14] CLASON C, CHRISTIAN, KUNISCH K, et al. Minimal invasion: an optimalL∞state constraint problem[J]. ESAIM: Mathematical Modelling and Numerical Analysis, 2010, 45(3): 505-522. [15] HINTERMüLLER, LIER M, ITO K, et al. The primal-dual active set strategy as a semi-smooth Newton method[J]. Journal on Optimization, 2003, 13(3): 865-888. [16] ULBRICH M. Semi-smooth Newton methods for operator equations in function space[J]. Journal on Optimization, 2003, 13(3): 805-842. [17] GOLUB G H, HEATH M, WAHBA G. Generalized cross-validation as a method for choosing a good ridge parameter[J]. Technometrics, 1979, 21(2): 215-223. [18] CHOI K, CHANG F K. Identification of impact force and location using distributed sensors[J]. AIAA Journal, 1996, 34(1): 136-142. [19] YAN G, ZHOU L. Impact load identification of composite structure using genetic algorithms[J]. Journal of Sound and Vibration, 2009, 319(3/4/5): 869-884. [20] ZHOU K, DOYLE J C, GLOVER K. Robust and optimal control[D]. New Jersey: Prentice Hall, 1996. Application ofL∞norm fitting regularization method in dynamic load identification of space-crafts GAO Wei, YU Kaiping, GAI Xiaonan (Department of Astronautic Science and Mechanics,Harbin Institute of Technology,Harbin 150001, China) Based on the variable limit integral theory, the weighted variable limit integral of response function was constructed with the least squares estimation technique. By performing the integral moving average method several times, the high-frequency noise in the measured noise was filtered effectively. Aiming at the residual low-frequency noise in the measured response, theL∞norm fitting regularization method was used for load identification. In order to realize this regularization method, a monotonicity validation method was proposed to select the optimal regularization parameters. The numerical simulation and the test verification showed that the proposed monotonicity validation method can determine the optimal regularization parameters of theL∞norm fitting regularization method effectively; in addition, the identified load is more accurate and more reliable than that using the traditionalL2norm regularization method; aiming at the characteristics of noise in telemetry data, the impact load is identified effectively by using theL∞norm fitting regularization method and simulated telemetry data. load identification;L∞norm regularization method; moving average; telemetry data 國家自然科學基金資助(11372084) 2015-11-13 修改稿收到日期:2016-02-25 高偉 男,博士生,1981年生 于開平 男,教授,1968年生 O327 A 10.13465/j.cnki.jvs.2017.09.0162 L∞范數擬合正則化方法

3 最優正則化參數選取方法


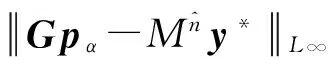
4 數值仿真及試驗驗證







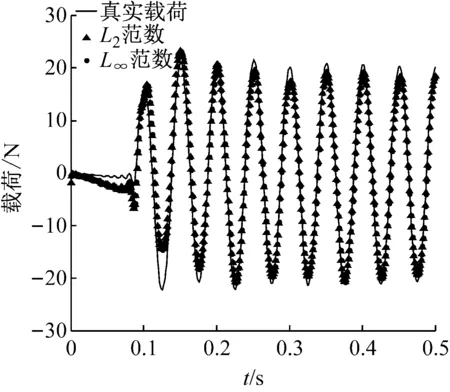
5 模擬遙測數據沖擊載荷識別

6 結 論

