變曲率FGM拱的面內自由振動分析

李萬春， 滕兆春

(蘭州理工大學 理學院，蘭州 730050)

變曲率FGM拱的面內自由振動分析

李萬春， 滕兆春

(蘭州理工大學 理學院，蘭州 730050)

基于Euler-Bernoulli曲梁理論，考慮材料沿拱厚度方向呈梯度分布時中性層的改變，將變曲率功能梯度材料(Functionally Graded Materials, FGM)拱在弧線方向離散成多個曲拱單元。視每個曲拱單元為半徑一定的圓弧拱單元，根據Hamilton變分原理推導出FGM圓弧拱單元的面內自由振動方程，進而求得了單元傳遞矩陣。利用傳遞矩陣法(Transfer Matrix Method, TMM)推導出變曲率FGM拱的面內自由振動特征方程，求解兩端固定邊界條件下變曲率FGM拱面內自由振動的固有頻率，并將得到結果與現有文獻作了比較，證明TMM對求解該問題的有效性。分析了曲率變化系數和材料體積分數變化系數對變曲率FGM拱的面內自由振動頻率的影響。

變曲率； FGM拱； 面內自由振動； 頻率； 傳遞矩陣法

近年來，功能梯度材料(Functionally Graded Materials，FGM)以具有較高的力學性能越來越多的被應用和研究，其一般是由陶瓷和金屬按指定的方向以一定的分布規律復合而成。對FGM性能的研究也成為結構設計及優化的重要內容，當然研究FGM結構的自由振動特性也有著十分重要的意義。Chakraborty等[1]基于一階剪切變形理論研究了FGM直梁的自由振動問題，論證了FGM與均勻材料在動力問題上的差異。Goupee等[2]應用差分法通過對FGM材料組份的調整，進一步優化了FGM結構的自由振動特性。Malekzadeh等[3]根據層合理論和微分求積法研究了層合圓弧拱的面內自由振動，得出拱的幾何參數和材料性能對自由振動結果的影響。Lü等[4]基于二維彈性理論、利用狀態空間法研究了層合圓弧拱的固有頻率與拱型幾何參數和材料疊加順序之間的關系。Tseng等[5]以Timoshenko曲梁為模型，在考慮剪切變形和轉動慣量等因素的條件下對變曲率復合材料層合梁的自由振動進行了研究，求得了變曲率層合曲梁面內自由振動頻率的精確解。Lim等[6]使用Fourier級數展開的方法分析了溫度場中FGM圓弧拱的面內振動，討論了功能梯度指數、溫度和幾何參數對振動頻率的作用。Carlos等[7]結合FGM曲梁中性軸的變化推導出運動方程，通過冪級數法揭示了FGM曲梁的動力特性。Zeng等[8]采用二維彈性法對Mori-Tanaka和自洽兩種FGM模型的拱進行了分析，評估功能梯度指數和拱型幾何參數在兩種模型中所得的不同自由振動頻率。Ugurcan[9]通過梁理論方法，考慮軸向變形、剪切變形、轉動慣量以及材料特性受溫度的影響等因素，給出了熱環境中FGM圓弧梁的面內自由振動規律。

本文基于Euler-Bernoulli曲梁理論，考慮材料沿拱厚度方向呈梯度分布時中性層的改變，將變曲率FGM拱沿弧線方向離散成多個曲拱單元。對每個曲拱單元，將其視為半徑一定的圓弧拱單元，根據Hamilton變分原理[10]推出FGM圓弧拱單元做面內自由振動時徑向位移所滿足的微分方程，用傳遞矩陣法(Transfer Matrix Method，TMM)[11]建立變曲率FGM拱的面內自由振動特征方程，相對于上述研究方法，TMM能夠通過小型矩陣解決大型結構的動力分析，并且還兼具求解思路清晰、計算過程簡單等優勢。最后通過算例計算總張角固定、曲率沿張角呈線性變化的變曲率FGM拱的面內自由振動頻率，分析了曲率變化系數和材料體積分數變化系數對自由振動頻率的影響。同時，將變曲率FGM拱退化到均勻材料圓弧拱，并和文獻[12]的有限元計算結果作了對比，結果完全吻合，說明應用TMM研究變曲率FGM拱的面內自由振動問題有效。

1 計算模型及控制方程

1.1 計算模型的建立

(a)(b)

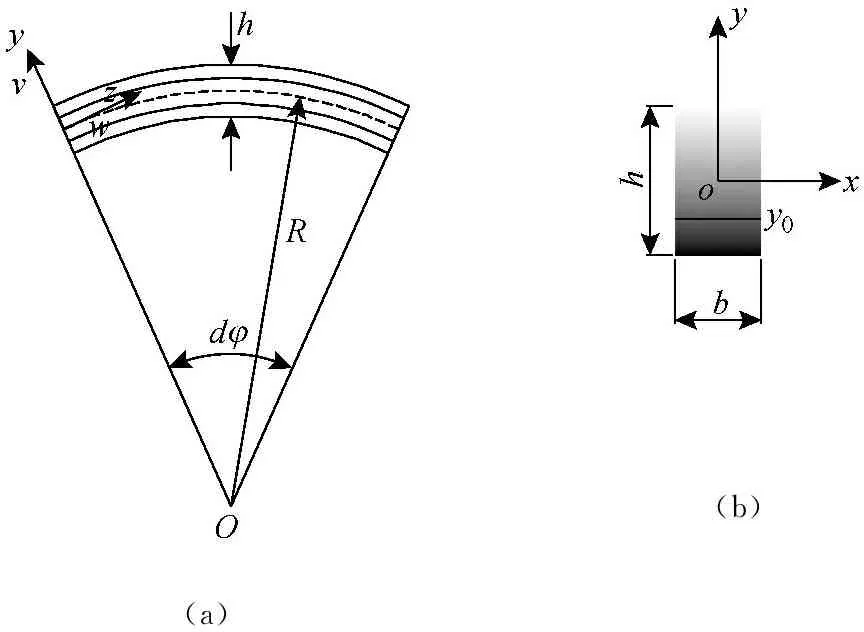
圖1 FGM圓弧拱的曲線坐標系

Fig.1 The curvilinear coordinate system of a FGM circular arch

圖1中R為拱單元幾何中面的曲率半徑，dφ為拱單元所對應的張角，h，b為拱單元截面的幾何尺寸，v，w為拱單元做面內自由振動時的徑向、周向位移，y0為拱單元橫截面中性層的位置。

1.2 曲率及材料梯度變化規律

考慮曲率沿張角呈線性變化，FGM由陶瓷和金屬復合而成，其中金屬相的體積分數沿拱厚度方向呈冪律分布，即

κ=κ0+k·φ

(1)

(2)

式中：κ、κ0、k和φ分別為拱軸線任一點處的曲率、初曲率、曲率變化系數和拱軸線任一點的張角，且k的單位為(rad·m)-1；p為金屬相體積分數變化系數。

1.3 橫截面中性層位置的確定

對沿拱厚度方向呈冪律分布的FGM橫截面，其中性層[13]隨梯度指數的變化而變化，如圖1所示，若中性層為y=y0，根據平面假設，拱的應變為

ε=(y0-y)/R*

(3)

式中,R*=R+y0為中性層的曲率半徑。根據線彈性材料的本構關系，有

陶瓷的應力

σc=Ecε

(4)

金屬的應力

σm=Emε

(5)

式中,Ec、Em分別為陶瓷和金屬的彈性模量。

由復合材料力學得，拱上任一點的總應力為

σ=[1-f(y)]σc+f(y)σm

(6)

由此可得平衡方程

(7)

結合式(3)～式(6)，由式(7)可得中性層的位置

(8)

1.4 控制方程的推導

如圖1所示FGM圓弧拱單元，對沿拱厚度呈式(2)分布的FGM拱單元，其材料性質有如下規律[14]

(9)

(10)

式中，ρc、ρm分別為陶瓷和金屬的質量密度。取徑向坐標為y，厚度為dy的橫截面，將其視為均勻材料的圓弧拱層，設其為圓弧拱的第K層，對均勻材料圓弧拱，其兩端彎矩和軸力有如下關系[15]

(11)

(12)

根據Hamilton變分原理，在時間區段[t1,t2]上有

(17)

將式(15)和式(16)代入式(17)中，而后對各項進行分部積分計算，其中有位移在時刻t1、t2上的變分為0，即

(18)

并結合邊界條件，有

簡支邊界

(19)

(20)

固定邊界

(21)

(22)

這樣，對式(17)進行化簡，經整理可得簡支或固定邊界條件下FGM圓弧拱的面內自由振動控制方程

(23)

(24)

對式(23) 進行弧長s的一階微分，式(24) 兩邊同時除以R*，而后兩式相加，經化簡可得

(25)

考慮FGM圓弧拱軸向不可伸長，即

(26)

故式(25)進一步得到簡化，得

(27)

在忽略切向慣性力的影響時，有

(28)

根據文獻[12]得到拱軸不可壓縮，忽略剪力、轉動慣量和切向慣性力影響時FGM圓弧拱做面內自由振動時徑向位移滿足的微分方程，即控制方程

(29)

又根據圓弧拱ds=R*dφ，故式(29)又可化為

(30)

2 傳遞矩陣及特征方程

2.1 單元傳遞矩陣

式中,U、V、θ、M、Q、N分別為對應節點處的軸向位移、徑向位移、轉角、彎矩、剪力和軸力。

根據控制方程(30)，假設該拱做簡諧振動，有

v=Vcosωt

(33)

將式(33)代入式(30)中，得

(34)

式(34)中

(35)

若設式(35)中

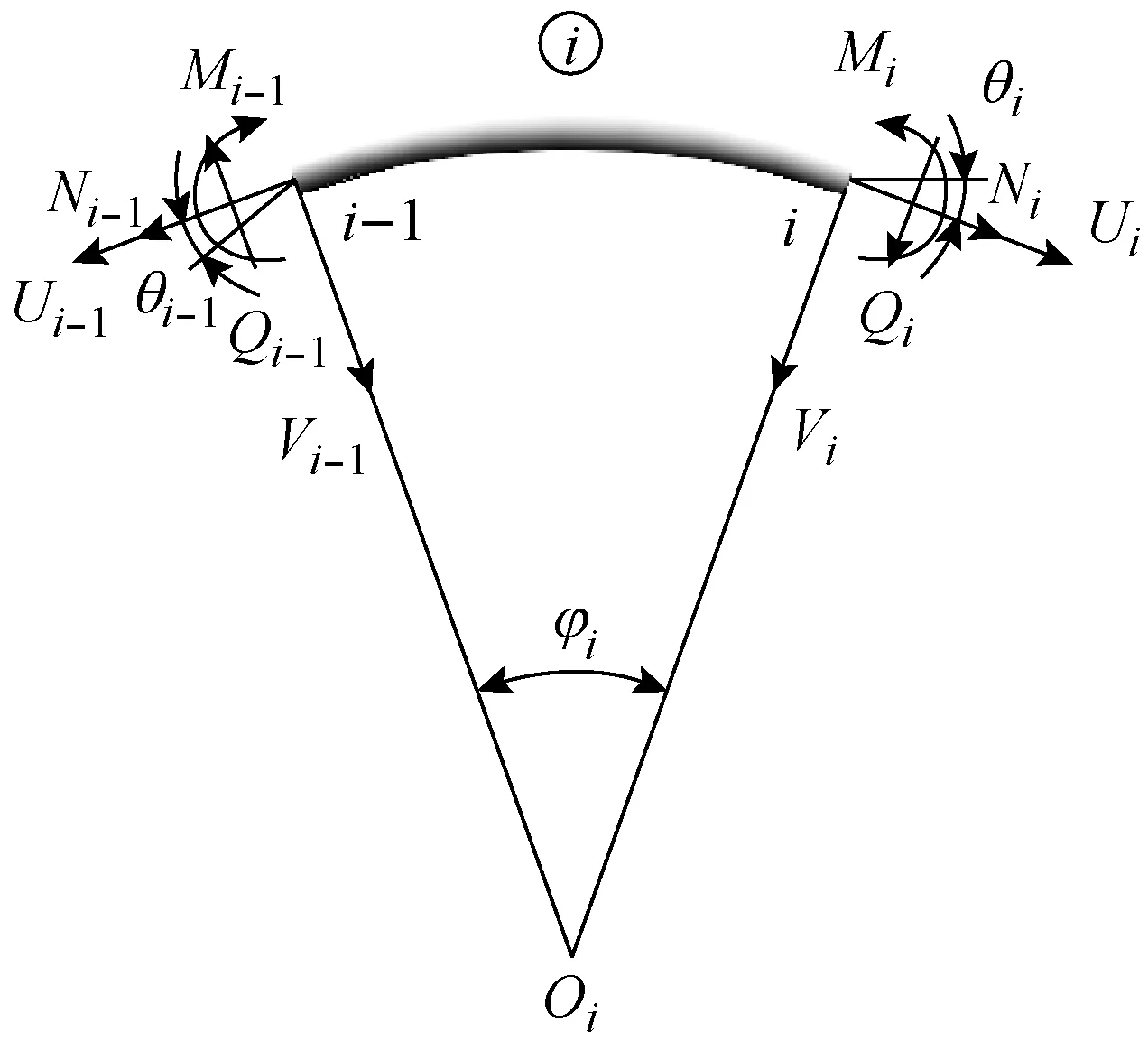
圖2 單元○i狀態模量分析

(36)

求解式(34)，有

(1) 當λ≥1時，令

(37)

則式(34)的解為

V=C1+C2ch(βφ)+C3sh(βφ)+C4cos(αφ)+C5sin(αφ)

(38)

由式(38)可進一步求得U、θ、M、Q和N分別為

(39)

(40)

(41)

(42)

(43)

(2) 當0<λ<1時，令

(44)

同理可解得式(34)，進一步得出U、θ、M、Q和N分別為

V=C1+C2cos(αφ)+C3sin(αφ)+C4cos(βφ)+C5sin(βφ)

(45)

(46)

(47)

(48)

(49)

(50)

Si-1=Ti-1C

(51)

Si=TiC

(52)

式中,C=[C1,C2,C3,C4,C5,C6]T。由此得

(53)

將式(53)代入式(52)中，得

(54)

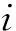
(55)

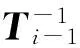
(56)

對節點i處，有φ=φi，同理將其代入式(38)～式(43)中， 并將這6組方程寫成矩陣形式，可得Ti

(57)

由式(55)即可以得出λ≥1時的單元傳遞矩陣Hi。同理當0<λ<1時有

(58)

(59)

由式(55)又得出0<λ<1時的單元傳遞矩陣Hi。

2.2 總傳遞矩陣

Ri=Rφi/2

(60)

根據各相鄰FGM拱單元間的連續性，即任一單元左端的狀態模量是與其相鄰上一單元右側的狀態模量，任一單元右側的狀態模量是與其相鄰下一單元左側的狀態模量，若設變曲率FGM拱單元始端的狀態模量為S0，則任一端的狀態模量Si與始端狀態模量S0有如下關系

Si=Hi·Hi-1·Hi-2…H2·H1·S0

(61)

整個變曲率FGM拱劃分為n段，則末端狀態模量與始端狀態模量之間的關系有

Sn=Hn·Hn-1…Hi…H2·H1·H0=H·S0

(62)

式中,H為變曲率FGM拱的總傳遞矩陣，且

H=Hn·Hn-1…Hi…H2·H1·H0

(63)

求得了各FGM圓弧拱單元的單元傳遞矩陣，根據式(63)即可求得變曲率FGM拱的總傳遞矩陣。

2.3 特征方程

對于拱型結構的邊界條件，在式(31)、式(32)中所設狀態模量均能找到3個元素為0，這樣，結合線性代數[16]中關于齊次線性方程組有非零解的充要條件的相關知識，在H中的對應元素所構成的行列式要等于0，即

Δ(α,β,λ)=0

(64)

將式(37)或式(44)代入式(64)中，結合式(35)得變曲率FGM拱面內自由振動的特征方程

Δ(ω)=0

(65)

求解式(65)，即可求得變曲率FGM拱的面內自由振動的頻率和相應的振型。

3 算例分析

曲率按式(1)、材料按式(2)連續變化的矩形截面變曲率FGM拱，其張角φ=5π/9rad，截面尺寸b×h=0.3 m2×0.8 m2，拱的左端點處的半徑、即初始半徑R0=60 m，約束為兩端固定。材料相關物理參數如表1所示。

表1 陶瓷和金屬的物理參數

當取曲率變化系數k=0、金屬相體積分數變化系數p→+∞時，變曲率FGM拱便退化到各向同性均勻材料金屬圓弧拱。

表2給出了在曲率固定，即κ=κ0=1/60的金屬圓弧拱在分段數為20時的前五階面內自由振動頻率ω的計算結果，并和文獻[12]的有限元計算結果作了比較。由表2可以看出，即使在分段數較少的情況下(這里n=20)，本文得出的結果與文獻[12]的有限元計算結果比較吻合，相對誤差在0.4%以內，顯示了利用TMM解決此類問題的適用性和精確性。

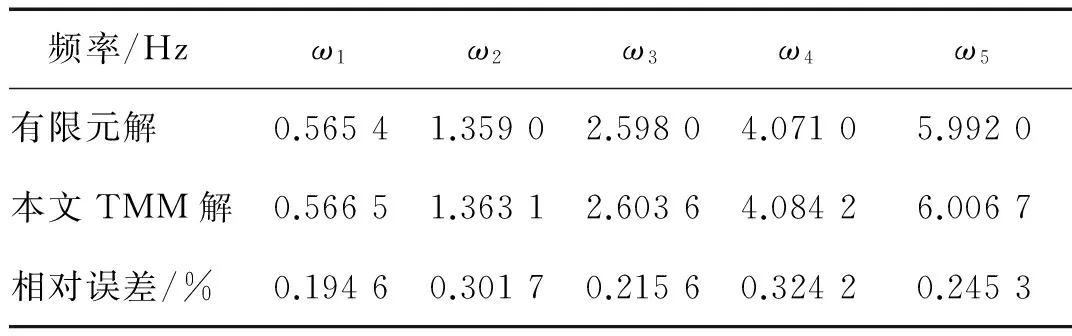
表2 金屬圓弧拱的面內自由振動頻率ω

變曲率FGM拱的前四階面內自由振動頻率ω與曲率變化系數k對應的關系曲線如圖3，其中曲率變化系數k∈[-1/6 000,1/6 000]，p∈[0,+∞),n=20。由圖3(a)～圖3(d)看出，在體積分數變化系數p一定時，變曲率FGM拱的前四階面內自由振動頻率ω與曲率變化系數k基本都呈線性變化關系，ω值隨著k值的增大而增大，且p值越小，這種線性比例關系越明顯。

變曲率FGM拱的前四階面內自由振動頻率ω隨材料體積分數變化系數p對應的關系曲線如圖4，其中p∈[0,100]。由圖4(a)～圖4(d)可以看出，在曲率變化系數k一定時，變曲率FGM拱的前四階面內自由振動頻率都隨體積分數變化系數p的增大而減小，且在p∈(0～10)時遞減最為劇烈。當p足夠大時，隨p繼續增大，ω的值趨于穩定，也反映了變曲率FGM拱的面內自由振動頻率是從陶瓷材料向金屬材料過渡的特點。

4 結 論

本文基于Euler-Bernoulli曲梁理論，考慮材料沿拱厚度方向呈梯度分布時中性層的改變，利用TMM研究變曲率FGM拱的面內自由振動問題。首先將變曲率FGM拱沿弧線方向離散成多個FGM曲拱單元，視每個FGM曲拱單元為半徑一定的FGM圓弧拱單元，根據變分原理推導出FGM圓弧拱單元的面內自由振動方程，進而用TMM導出了FGM圓弧拱單元兩端狀態模量的單元傳遞矩陣和變曲率FGM拱的總傳遞矩陣，最后結合邊界條件及線性代數中關于齊次線性方程組有非零解的充要條件的相關知識，求得變曲率FGM拱面內自由振動的各階頻率。將所得到的解退化到各向同性均勻材料圓弧拱情況下的結果，與已有的有限元解一致。結果表明本文所建立的拱結構力學模型可靠，理論公式推導正確。由適用條件和精度要求可見，本文所采用的方法是適用于解決變曲率FGM拱的面內自由振動問題的，是分析變曲率FGM拱面內自由振動特性的一種行之有效的方法。

(a) 一階頻率

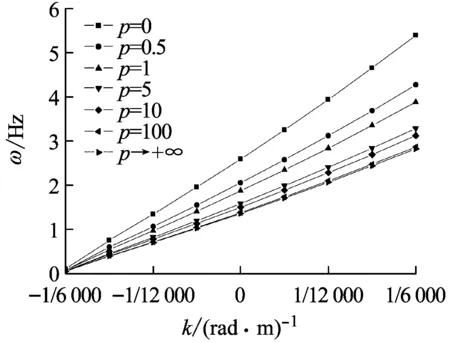
(b) 二階頻率

(c) 三階頻率

(d) 四階頻率

Fig.3 Dependence of the curvature coefficientkof variation on the first four in-plane free vibration frequencies of FGM arches variable curvature

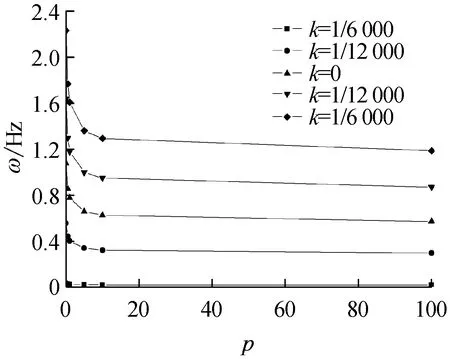
(a) 一階頻率

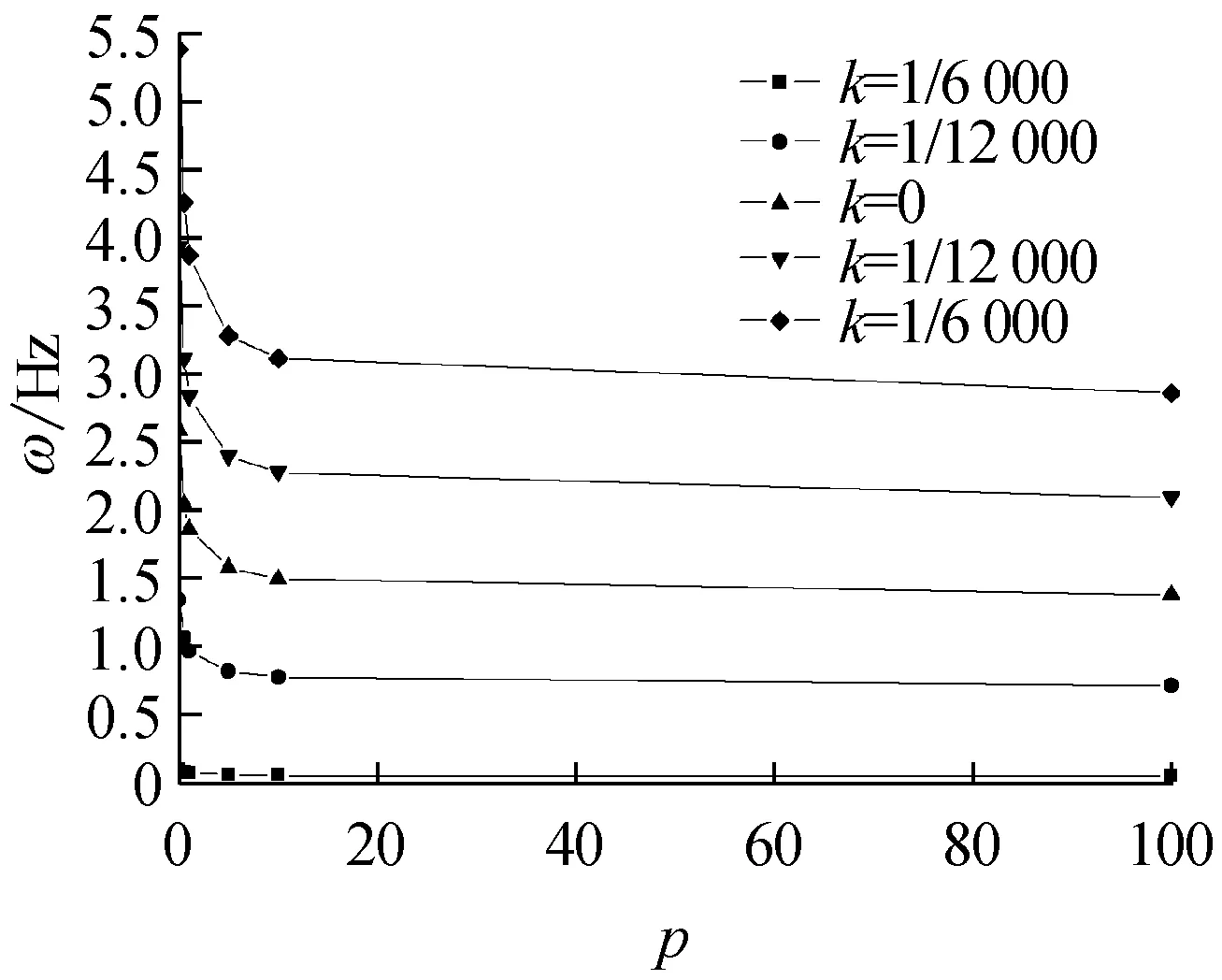
(b) 二階頻率

(c) 三階頻率

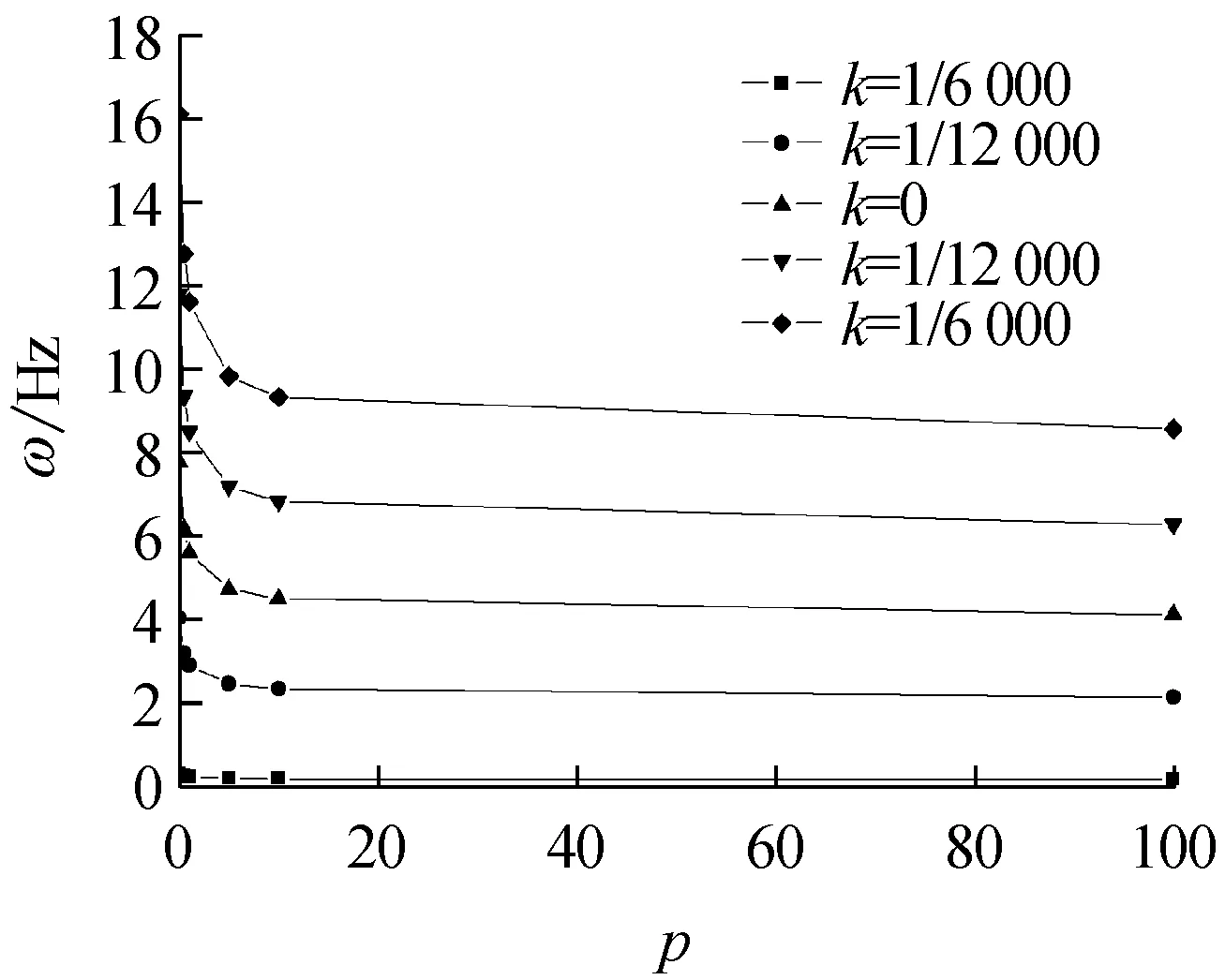
(d) 四階頻率

Fig.4 Dependence of material volume fractionpof variation on the first four in-plane free vibration frequencies of FGM arches with variable curvature

[1] CHAKRABORTY A, GOPALAKRISHNAN S, REDDY J N. A new beam finite element for the analysis of functionally graded materials[J]. International Journal of Mechanical Sciences， 2003, 45(3):519-539.

[2] GOUPEE A J, VEL S S. Optimization of natural frequencies of bidirectional functionally graded beams[J]. Structural and Multidisciplinary Optimization, 2006, 32(6):473-484.

[3] MALEKZADEH P, SETOODEH A R, BRRMSHOURI E. A hybrid layerwise and differential quadrature method for in-plane free vibration of laminated thick circular arches[J]. Journal of Sound and Vibration, 2008, 315(1/2): 212-225.

[4] Lü Q, Lü C F. Exact two-dimensional solutions for in-plane natural frequencies of laminated circular arches[J]. Journal of Sound and Vibration, 2008, 318(4/5): 982-990.

[5] TSENG Y P，HUANG C S，KAO M S. In-plane vibration of laminated curved beams with variable curvature by dynamic stiffness analysis[J]. Composite Structures, 2000, 50(2): 103-114.

[6] LIM C W, YANG Q, Lü C F. Two-dimensional elasticity solutions for temperatire-dependent in-plane vibration of FGM circular arches[J]. Composite Structures, 2009, 90(3): 323-329.

[7] CARLOS P F, MARCELO T P. The dynamics of thick curved beams constructed with functionally graded materials[J]. Mechanics Research Communications, 2010,37(6):565-570.

[8] ZENG Q C, LIM C W, Lü C F, et al. Asymptotic two-dimensional elasticity approach for free vibration of FGM circular arches[J]. Mechanics of Advanced Materials and Structures, 2012, 19(1/2/3):29-38.

[9] UGURCAN E. In-plane free vibrations of circular beams made of functionally graded material in thermal environment: Beam theory approach[J]. Composite Structures, 2015, 122:217-228.

[10] 胡海昌. 彈性力學的變分原理及其應用[M]. 北京: 科學出版社, 1982.

[11] 向天宇, 鄭建軍. 變截面圓拱的自由振動[J]. 振動與沖擊, 2000, 19(2):59-63.

XIANG Tianyu, ZHENG Jianjun. Free vibration of circular arches with variable cross-section[J]. Journal of Vibration and Shock, 2000, 19(2):59-63.

[12] ZHAO Y Y, KANG H J. In-plane free vibration analysis of cable-arch structure[J]. Journal of Sound and Vibration, 2008, 312(3): 363-379.

[13] 孫訓方, 方孝淑, 關來泰. 材料力學[M]. 北京: 高等教育出版社, 1982.

[14] LI S R, SU H D, CHENG C J. Free vibration of functionally graded material beams with surface-bonded piezoelectric layers in thermal environment[J]. Applied Mathematics and Mechanics (English Edition), 2009, 30(8): 969-982.

[15] VIOLA E, ARTIOLI M, DILENA M. Analytical and differential quadrature results for vibration analysis of damaged circular arches[J]. Journal of Sound and Vibration, 2005, 288(4/5): 887-906.

[16] 同濟大學數學教研室. 線性代數[M]. 北京: 高等教育出版社, 1999.

In-plane free vibration analysis of FGM arches with variable curvature

LI Wanchun， TENG Zhaochun

(School of Science, Lanzhou University of Technology, Lanzhou 730050, China)

Based on the theory of Euler-Bernoulli curved beam, the shifting of neutral layer was considered when materials were gradually distributed trapezoidally along the arch thickness, and functionally graded material (FGM) arches with variable curvature were discretized into a number of curved arch elements along the arc direction. Every curved arch element was considered as a circular arch element with a constant radius, according to Hamilton variational principle, the in-plane free vibration equation of a FGM circular arch element was derived, then the element transfer matrix was deduced. Furthmore, using TMM, the in-plane free vibration characteristic equation of the FGM arch with variable curvature was derived, the in-plane free vibration natural frequencies of the FGM arch with variable curvature under two-clamped end boundary condition were solved, the results were compared with those previously reported. It was shown that TMM is effective to solve this problem. The influences of curvature varying coefficient and material volumn fraction varying coefficient on the in-plane free vibration frequencies of the FGM arch with variable curvature were analyzed.

variable curvature; functionally graded materials arches; in-plane free vibration; frequency; transfer matrix method

國家自然科學基金(11662008)；甘肅省自然科學基金(148RJZA017)

2016-01-08 修改稿收到日期：2016-03-16

李萬春 男，碩士生，1984年生

滕兆春 男，副教授，1969年生

O343

A

10.13465/j.cnki.jvs.2017.09.030