讀懂計算教學的價值所在

【摘要】運算能力是數學能力的核心要素，是數學學科獨有的能力。在數學計算教學中，教師應突出學習計算的價值，幫助學生理解運算的算理，尋求合理簡潔的運算途徑解決問題。

【關鍵詞】數學計算教學；運算能力；價值

【中圖分類號】G623.5 【文獻標志碼】A 【文章編號】1005-6009（2017）25-0074-02

【作者簡介】荊亞琴，江蘇省常州市新北區龍虎塘實驗小學（江蘇常州，213000）教師，一級教師，常州市數學學科帶頭人。

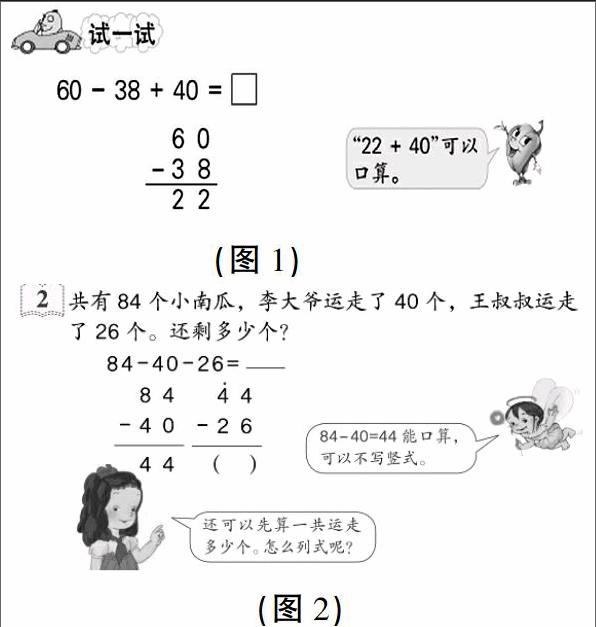
近日，筆者所在年級的同事在備課蘇教版二上第5頁“試一試：60-38+40”時出現了不同意見，原因是教材中提到“22+40”可以口算（如圖1），有的教師認為學生剛接觸連加連減豎式，還沒有掌握好就要改變計算方法，很可能掌握不牢，提倡22+40也列豎式計算，提高正確率。也有的教師認為就應該按照教材的要求，22+40能口算的，就口算。那么這道算式該如何教？如何處理筆算與口算之間的關系呢？

“數與運算”是小學數學教材中的重要內容，其對象是自然數、分數和小數，包括數的認識與數的運算。我國傳統的數學教學強調的是數運算的快速性與準確性，在新課標實施以前，教學大綱對學生運算能力的要求是：“正確、迅速、合理、靈活”，尤其以準確率和速度作為衡量運算能力的標準。正因此，說到運算，很多教師立刻想到“熟能生巧”，認為數學運算能力無非就是依靠多練習，練速度，練正確率。

新課改以來，與運算能力密切相關的數感、符號感進入數學教育的視野，《義務教育數學課程標準（2011版）》明確提出把“運算能力”作為十大核心詞之一。運算能力主要是“能夠根據法則和運算律正確地進行運算的能力，培養運算能力有助于學生理解運算的算理，尋求合理簡潔的運算途徑解決問題。”能夠按照一定的程序進行運算只能稱之為運算技能；“運算能力”不僅是數學操作技能，還包括觀察、記憶、思維、聯想等有關的從低級到高級的綜合能力，是一種數學思維能力。

筆者查閱了其他相關版本的教材，發現蘇教版和人教版（如圖2）在教學連加、連減和加減混合的筆算時，都不約而同提到了“能口算的可以不寫豎式”。

蘇教版和人教版都將100以內的連加、連減和加減混合的計算教學，安排在了小學二年級上學期進行。首先：教材將筆算教學與解決問題的教學有機結合，先從現實情境中提出要解決的計算問題，突出學習計算的價值。不論是蘇教版中的“38+42+33”，還是人教版中的“28+34+32”，讓學生明確連加、連減或加減混合運算的一般方法是按照同級運算從左往右，依次計算。此外，不論是蘇教版的試一試，還是人教版的例2，都努力幫助學生在挖掘信息的基礎上，選擇解決問題的最佳運算方法，如能口算的就不寫豎式，從而使運算過程更簡單；這恰恰是在幫助學生養成根據參與運算的數據特點靈活選擇算法的自覺意識，能口算的應該大膽口算。該內容的教學，指向的是對數的認識與數的運算的“理解”，而不是指向快速準確計算的目標。“理解”強調的是對數之間關系的認識，是對算理的把握，而快速計算側重的是對算法的熟悉乃至自動化操作，二者有著截然不同的價值取向。因此，將合理選擇算法滲透到筆算教學中，不僅有利于突出運算思維的推理成分，更有利于提升學生的運算策略水平。

事實上，平時的數學教學，教師為了追求口算的速度和筆算的正確率，往往習慣將口算與筆算“割裂”教學。正因如此，教學到二年級《加減混合》這一內容時，即使意識到要讓學生掌握靈活的計算方法，但為了追求計算的準確性，教師認為還是選擇豎式計算更為穩妥。其實，筆算僅僅是記錄計算過程與結果的書面形式，一味地強調豎式筆算，雖然能較快實現技能目標，卻也容易造成學生算法認知上的缺陷，以及由此帶來的運算程序僵化。再如看到“靈活運算”，教師往往把靈活運算等同于簡便計算。傳統的簡便運算局限于根據運算定律、運算性質將算式變形，這與問題解決策略多樣化和尋求合理簡潔的運算途徑解決問題，還存在較大差距。靈活運算不僅涵蓋簡便計算的任何一道題，更要讓學生在解決問題的過程中運算簡便。

這不禁讓筆者聯想到一次對全校五年級學生調研時的運算題“3.07-0.19×2-1.62”，大約有36%的學生采用以下的方法進行計算。

從追求運算的正確性來說，該題答案正確，學生按照兩級運算規則來答題，先算乘除，再算加減。再細細思考，學生在簡化運算能力方面卻暴露了薄弱之處。簡化運算能力，是學生解決問題過程中的優化手段，是在正確合理的方法指導下，使運算過程變得更簡潔。如果教師在運算教學中一味追求運算結果的正確率，偏重準確的結果，必然會對題目缺少深入的理解與思考，難以選擇解決問題的最佳運算方法，從而會將學生的思維禁錮在機械模仿和記憶的初級水平上。

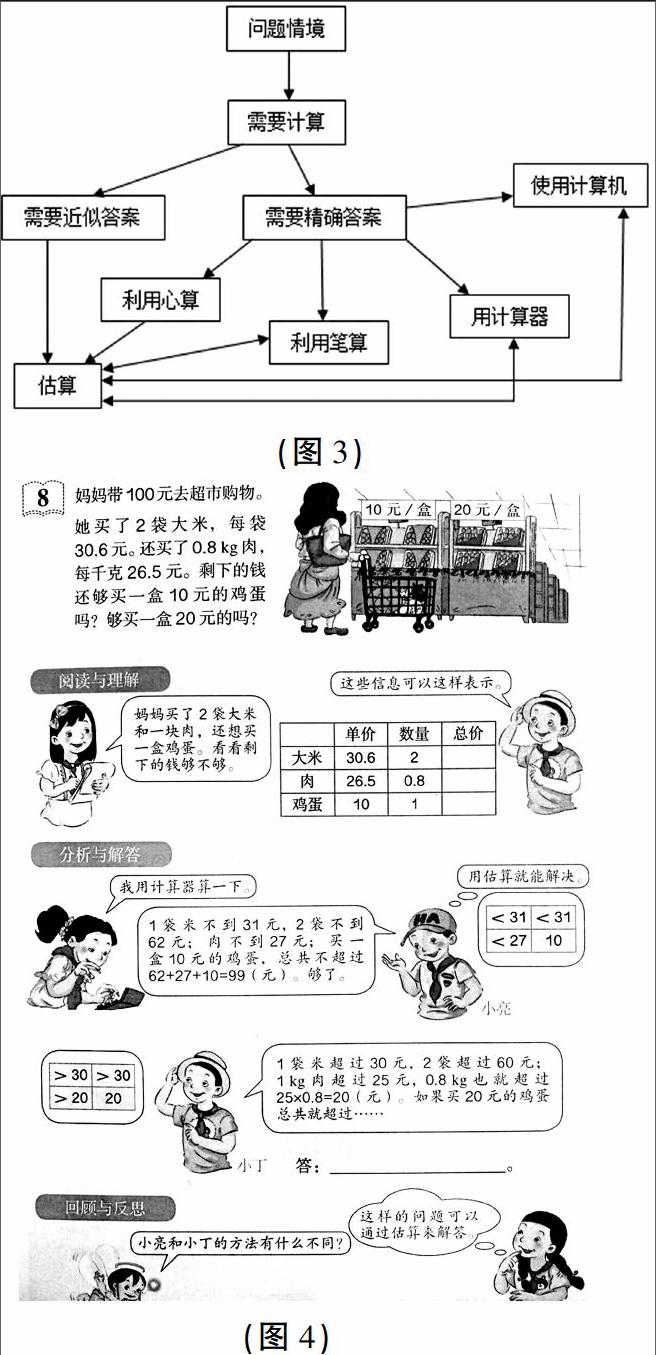
關于運算，美國數學教師學會在1989年編寫的《學校數學課程與評價標準》中有一段論述（如圖3），反映了其對運算基本概念的理解。當面臨實際問題進行計算時，首先應當考慮需要近似答案還是精確答案：如果一個近似答案就足夠了，那就估算；如果需要精確答案，那就要依次選擇口算、筆算，是否需要使用計算器算等。也就是說，選擇計算方法，應在確定了計算方式之后進行。

人教版五上的一道例題（如圖4）就較好地詮釋了面對實際問題時如何選擇適合的方法來解決。

隨著課程改革的實施與深化，計算已不再作為獨立的內容進行教學。教師要把學習計算與解決問題的過程結合起來，凸顯計算是解決問題的手段，解決問題是計算的目的。通過計算教學培養數感，包括借助計算器探索規律，發展數與運算的概念，都是為了提升人的數學素養與運算能力。