一種用于異步電機無速度傳感器控制的自適應滑模觀測器

高艷霞， 陳靜， 范應鵬， 宋文祥

(上海大學 機電工程與自動化學院，上海 200072)

一種用于異步電機無速度傳感器控制的自適應滑模觀測器

高艷霞， 陳靜， 范應鵬， 宋文祥

(上海大學 機電工程與自動化學院，上海 200072)

針對異步電機無速度傳感器中存在的對參數變化魯棒性差的問題，研究了一種基于自適應滑模觀測器的異步電機無速度傳感器的矢量控制方案。自適應滑模觀測器根據電機靜止坐標系下的數學模型構造了轉子磁鏈觀測器，定子電流觀測值與實際值的誤差構成觀測器的滑模面，在滑模運動下該觀測器的觀測值最終趨近于實際值，從而實現轉子磁鏈的估計。電機轉速由自適應方法估算得到，滑模觀測器的穩定性可由李雅普諾夫穩定性證明。與其他方案相比，該方法的優點在于實現簡單，對參數變化具有魯棒性。仿真和實驗對控制方案的正確性和可行性給出了驗證，該觀測器可以實現對轉子磁鏈和轉速的觀測，且在負載擾動和給定轉速變化的情況下該滑模觀測器具有魯棒性。

異步電機；自適應滑模觀測器；無速度傳感器；矢量控制；魯棒性

0 引 言

異步電機的低成本、高可靠性，使其有廣泛的應用。矢量控制尤其是轉子磁場定向矢量控制是當前應用廣泛的一種經典異步電機驅動控制策略。在此基礎上，無速度傳感器矢量控制技術因其去除了編碼器，從而大大提高了交流傳動系統的可靠性,降低了系統的實現成本。準確計算轉子磁鏈和辨識電機轉速是實現無速度傳感器矢量控制的關鍵。

由于異步電機轉子磁鏈的直接測量十分困難，通常需要通過間接觀測計算獲得。目前，計算磁鏈的方法大致分為兩類，理想模型和非理想模型。非理想模型中，有齒諧波法和信號注入法[1]。文獻[1]在低速和零速運行狀態下，提出了磁場凸極反應理論。這些方法是依賴于電機對高頻信號注入的響應，其中的凸極效應依賴于磁場飽和和電機的幾何結構。這對測量的精準度要求很高，增加了矢量控制系統的軟硬件的復雜度。而且，當電機的凸極效應不明顯時，不足以使電機產生恰當的響應，需要合適的機械設計構造以增強凸極效應。理想模型中，有開環模型法和閉環模型法。開環模型分為電流模型法和電壓模型法[2]。其中，電流模型法受電機參數變化的影響較大，一般僅用于低速階段；而電壓模型法，因其存在積分運算問題，一般用于中高速運行階段。有時為提高準確度，把這兩種模型結合起來，在低速時采用電流模型，在中高速時采用電壓模型[3]。閉環模型中，分為模型參考自適應、全階觀測器[4]、擴展卡爾曼濾波器[5]、擴展龍伯格法以及滑模觀測器等。文獻[4]利用極點配置的方法對全階觀測器的反饋增益矩陣進行設計，加快了估計誤差的收斂速度。文獻[5]提出了一種基于抗差擴展卡爾曼濾波器的磁鏈和轉速估計方法,探討了在應用于感應電機轉速估計時抗差擴展卡爾曼濾波器能否同樣取得良好的估計精度,以期提高磁鏈和轉速觀測的準確性。文獻[6]從穩態精度、動態性能、低速運行、參數敏感性、噪聲敏感性和復雜性等方面對龍貝格觀測器，滑模觀測器和擴展卡爾曼濾波器進行了綜合分析和比較，三種觀測器在高速時穩態性能指標相差不大，其中，擴展卡爾曼濾波器具有最好的噪聲敏感性，龍貝格觀測器實用性最佳，但在參數敏感性和魯棒性方面，滑模觀測器性能明顯優于龍貝格觀測器和擴展卡爾曼濾波器。在這些方案中，滑模觀測器由于自身具有實現簡單，對系統干擾、參數變化和系統噪音具有魯棒性的特點，近些年來成為轉子磁鏈觀測的研究熱點[7-13,15]。

本文研究了一種轉速自適應滑模觀測器(sliding mode observer,SMO)，用于異步電機的矢量控制系統中。通過檢測電機定子電流和定子電壓作為觀測器的輸入，構造以定子電流估算誤差為滑模面的滑模觀測器，實現對電機轉子磁鏈的估算。電機轉速則通過自適應方法得到。最后，該觀測器通過仿真和實驗驗證了其可行性和有效性。

1 異步電機的數學模型

在靜止參考坐標系αβ下，選擇電機定子電流、轉子磁鏈作為狀態變量，異步電機的狀態方程可表示為：

px=Ax+Bvs。

(1)

式中，x，A，B三個量表示如下：

系統矩陣A，B表示如下：

A11=aI,A12=cI-dJ,A21=cI,

其中：p為微分算子；is為定子電流，is=(isαisβ)T；vs為定子電壓，vs=(vsαvsβ)T；ψr為轉子磁鏈，ψr=(ψrαψrβ)T；Rs，Rr為定子電阻和轉子電阻；Ls，Lr，Lm為定子電感，轉子電感和互感；σ為定子漏磁通系數；σr為轉子時間常數；ωr為電機轉子角頻率。

2 自適應滑模觀測器設計

轉子磁鏈估測的滑模觀測器建模如下：

(2)

其中,帶有“^”的量均為估算值，K為矩陣增益，sgn()表示符號函數。

當存在參數變化時，誤差方程表示如下：

(3)

所構造的滑模面為

(4)

由李雅普諾夫穩定性，可得

(5)

ei=pei=0。

(6)

式(3)化為

(7)

(8)

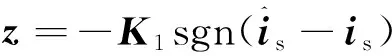
由式(7)和式(8)得，在滑模條件下，轉子磁鏈的誤差方程如式(9)所示：

(9)

當轉速已知且其他參數不變，則在滑模條件下的轉子磁鏈觀測器的誤差方程為

peψ=(A22+LA12)eψ。

(10)

當轉速為變參數時，則矩陣ΔA中各元素可表示為：

由此構造李雅普諾夫方程如下：

(11)

其中，W是修正項，其作用是保證在李雅普諾夫穩定理論下參數估測的收斂性。

假設：

pV=pV1+pV2。

(12)

其中：

(13)

(14)

且Λ=L-εI。

如果pV1<0并且pV2=0，則pV<0，顯然，在這種條件下滿足李雅普諾夫穩定性定理。

對于pV1<0，可選擇

ΛT=-γA12，γ>0。

(15)

在此基礎上，pV2=0使

(16)

由式(16)，函數W確定為

(17)

比較式(16)和式(17)，得到轉速自適應估算方程如下所示：

(18)

這就是李雅普諾夫穩定定義下轉速的自適應收斂律，為改善自適應律收斂速度，將自適應律改為比例積分形式[14]。式(19)中，kp，ki分別為比例和積分系數。

(19)

3 轉子磁鏈的收斂性分析

分析轉子磁鏈的收斂性，就是要分析磁鏈觀測誤差eψ能不能在有限的時間內收斂到零。重寫式(10)為

peψ=Aψeψ。

(20)

其中,Aψ=A22+LA12。

當磁鏈觀測誤差的初始值eψ(t0)≠0時，式(20)在時域的解為

eψ(t)=eAψteψ(t0)。

(21)

由式(21)可知，轉子磁鏈的觀測誤差eψ(t)的衰減速度取決于矩陣Aψ的特征值[14]。如果僅考慮使eψ盡快趨近于零，則應把特征值配置在s平面的左半平面且距虛軸很遠的地方。然而這樣配置特征值，會使觀測器的頻帶變得很寬，從而降低它對高頻噪音的抑制能力。因此，對矩陣Aψ特征值的設計，也即矩陣L的設計，應兼顧到觀測器的響應速度和抗干擾的要求。

由式(15)可知，矩陣L滿足l11=l22，l12=-l21,即對角線上的元素相等，副對角線的元素為相反數，則矩陣Aψ的元素也具有這樣的特征。因此，可以令Aψ為如下形式，其中α和β為實數。

(22)

矩陣Aψ的特征值λ求取如式(23)所示：

(-α-λ)2+β2=0。

(23)

則特征值λ也即磁鏈誤差的閉環特征根為

λ1,2=-α±jβ。

(24)

為滿足磁鏈觀測的收斂性，必須滿足

α>0。

(25)

所以在設計矩陣L時，要選擇合適的參數，滿足式(25)，使得觀測器的磁鏈收斂。

由式(15)，可知

(26)

(27)

因為式(15)中的約束條件為γ>0，故滿足α>0。此時磁鏈誤差系統有兩個相同的負實根λ1,2，為

當有兩個相異的負實部共軛虛根時，磁鏈誤差趨近于零的過程中呈衰減振蕩的形式，響應速度比有兩個相同的負實根時快，為此，重新定義矩陣L為式(28)，且仍滿足李雅普諾夫函數的要求即pV1<0。

(28)

此時，

故特征值如下:

上式滿足α>0，即保證了磁鏈誤差系統的特征根分布在左半平面，說明磁鏈具有收斂性。

保證磁鏈的收斂性，就是令磁鏈誤差系統的閉環特征根即矩陣的特征根分布在系統的左半平面，且越遠收斂速度越快，但同時也會使抗高頻干擾能力下降。在參數選取時，要在兩者之中折中處理。

在這里，需要確定6個參數，分別是q，γ，kp，ki，k1，k2。其中，q，γ的選取決定磁鏈估算的性能，而式(19)中的kp，ki決定轉速估算的性能，式(5)中的k1，k2決定電流估算的性能。文中4.1節給出了具體的參數選取和仿真結果。

圖1即異步電機的自適應滑模觀測器的原理框圖。

圖1 異步電機的自適應滑模觀測器Fig.1 Adaptive sliding mode observer of induction motor

觀測器輸入量為定子電壓和實際定子電流，在電機靜止坐標系下的狀態方程基礎上，利用估算定子電流和實際定子電流的誤差作為滑模面，構成狀態估算方程，實現對電機轉子磁鏈的估算。電機轉速則由自適應理論的李雅普諾夫函數得到。整個電機矢量控制系統框圖如圖2所示。

圖2 異步電機無速度傳感器矢量控制系統框圖Fig.2 Diagram of sensorless vector control of induction motor

4 仿真結果

為驗證本文的自適應滑模觀測器的性能，在Matlab/SIMULINK環境中建立了系統仿真模型。異步電機參數如表1所示。

表1 電機參數表Table 1 Parameters of induction motor

4.1 磁鏈收斂性仿真

為說明磁鏈具有收斂性，本節選取了三組參數q=0.1,γ=0.0001ε;q=0.2,γ=0.0001ε;q=0.2,γ=0.001ε進行仿真。圖3為磁鏈誤差系統的閉環特征根分布圖，圖(b)是圖(a)的局部放大圖。由圖3看出，特征根分布在左半平面，說明磁鏈誤差具有收斂性。

在4.2節和4.3節的仿真中，具體的參數選取為：q=0.2，γ=0.0001ε，kp=0.4，ki=30，k1=-100，k2=-100。

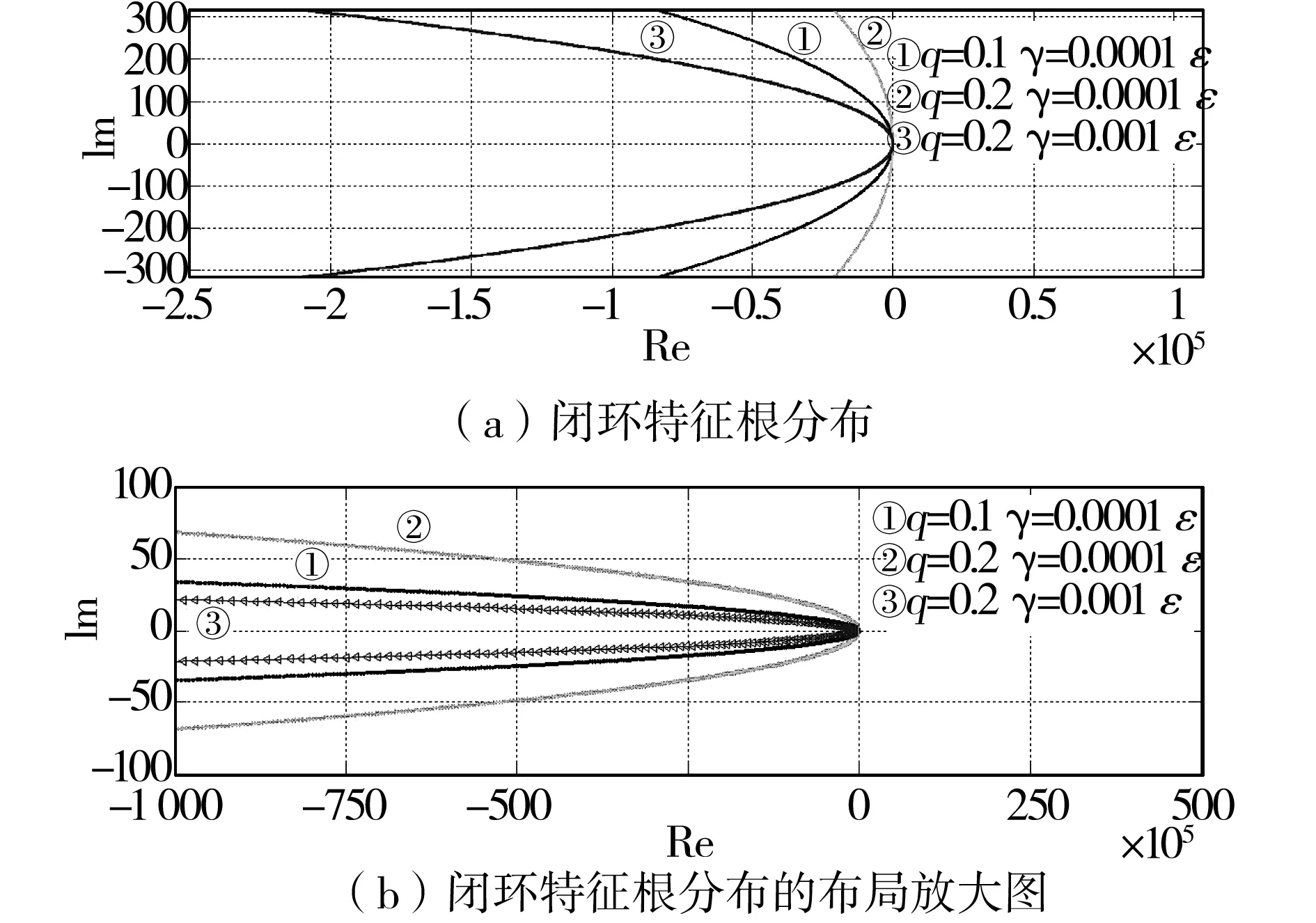
圖3 磁鏈誤差系統的閉環特征根分布Fig.3 Eigenvalues distribution of the flux error system

4.2 動態仿真結果

在t=0 s時空載啟動，給定轉速為1 200 r/min，仿真時間為0.8 s。文中分別給出了給定轉速突變和突增負載兩種情況下的動態仿真波形。

4.2.1 給定轉速突變

在t=0.5 s時轉速突減為600 r/min，定子電流，轉子磁鏈，轉子磁鏈角，轉速的仿真波形如圖4所示。轉子磁鏈，轉子磁鏈角，轉速三者的估算誤差的仿真波形如圖5所示。

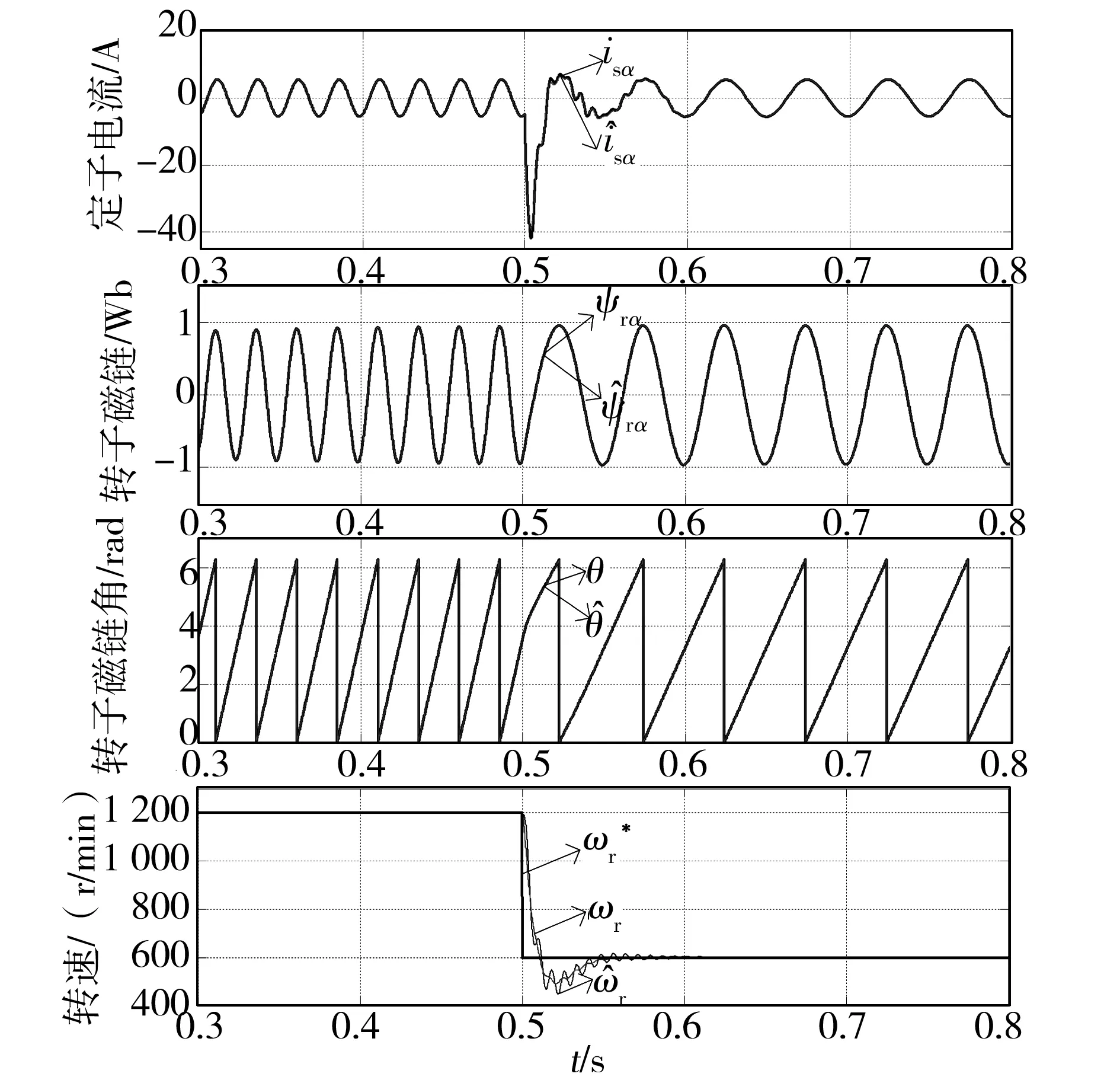
圖4 給定轉速突變時的定子電流，轉子磁鏈，轉子磁鏈角和轉速波形Fig.4 Waveforms of stator current, rotor flux,rotor flux angle and speed when the given speed is changed

圖5 給定轉速突變時的轉子磁鏈，轉子磁鏈角和轉速的估算誤差Fig.5 Error of rotor flux，rotor flux angle and speed when the given speed is changed

從圖4可以看出，定子電流，轉子磁鏈，轉子磁鏈角，轉速的跟蹤效果很好，估算值基本和實際值重合。圖5中轉子磁鏈，轉子磁鏈角，轉速的估算誤差分別為2.0%、0.4%、1.7%，均在可接受的誤差范圍內。

4.2.2 突增負載

在t=0.5 s時，負載由空載突增為額定負載25 N·m，定子電流，轉子磁鏈，轉子磁鏈角，轉速的仿真波形如圖6所示。轉子磁鏈，轉子磁鏈角，轉速三者的估算誤差的仿真波形如圖7所示。

從圖6可以看出，定子電流，轉子磁鏈，轉子磁鏈角，轉速的跟蹤效果同樣很好，估算值基本和實際值一樣。轉速在突增負載的動態過渡過程中略有偏差，但平穩之后跟蹤狀況良好。圖7中轉子磁鏈，轉子磁鏈角，轉速的估算誤差分別為1.0%、0.1%、1.1%，均在可接受的誤差范圍內。

從上述兩種情況的波形可以看出，電機在給定轉速突變和加載運行的情況下，無論是在動態過程還是穩態過程，各個估測量可以實時跟隨實際值，且估算誤差很小，均在可接受的范圍內。

4.3 參數魯棒性仿真結果

基于4.2節的仿真測試，在t=0.8 s改變電機的定子電阻和轉子電阻，仿真時間設置為1.1 s。觀察滑模觀測器對參數變化的魯棒性的適應性。

圖8(a)是Rs增加30%，Rr增加50%的轉子磁鏈及其誤差波形。圖8(b)是Rs增加50%，Rr增加70%的轉子磁鏈及其誤差波形。圖8(c)是Rs增加70%，Rr增加100%的轉子磁鏈及其誤差波形。圖8三種情況下轉子磁鏈的估算誤差分別為0.12%，0.17%，0.20%。可以看出，定子和轉子電阻的變化，對觀測器的精度有一定影響，但影響幾乎可以忽略，其估算誤差對觀測器的性能來說在可以接受的范圍內，證明該觀測器對參數變化具有較好的魯棒性。

圖6 突增負載時的定子電流，轉子磁鏈，轉子磁鏈角和轉速波形Fig.6 Waveforms of stator current, rotor flux,rotor flux angle and speed when the load is added

圖7 突增負載時轉子磁鏈，轉子磁鏈角和轉速的估算誤差Fig.7 Error of rotor flux，rotor flux angle and speedwhen the load is added

圖8 改變Rs，Rr時轉子磁鏈，轉子磁鏈角和轉速的估算誤差Fig.8 Error of rotor flux，rotor flux angle and speed when Rs and Rr are changed

5 實驗驗證

為充分驗證滑模觀測器的性能，在定點型DSP芯片TMS320F2812實驗平臺上進行了空載和加減載實驗。系統控制周期為250 μs。負載為與異步電機同軸連接的直流發電機。在加減載試驗中，通過調節直流發電機的勵磁電流，改變步電機的負載大小。異步電機安裝有測速編碼器，以得到電機真實轉速，便于與估測轉速進行對比。定子電流由霍爾傳感器測量得到，并在示波器上顯示，作為負載參考和相位參考。實驗中采用的電機參數如表1所示。

空載試驗中，給定轉速為750 r/min，空載電流為3.08 A。圖9為空載時滑模觀測器的定子電流，轉子磁鏈，轉子磁鏈角和轉速的波形。其中，iA為霍爾傳感器測得的定子A相電流。

圖9 空載時定子電流，轉子磁鏈和磁鏈角和轉速波形Fig.9 Waveforms of stator current，rotor flux，rotor flux angle and speed under no-load

為驗證滑模觀測器磁鏈觀測的正確性，圖10給出了滑模觀測器與全階觀測器[14](full-order observer, FO)在空載時的估算轉子磁鏈和轉子磁鏈角的對比圖。

圖10 兩種磁鏈觀測器結果對比Fig.10 Waveforms of actual and estimated rotor flux and rotor flux angle with SMO and FO under no-load

圖11為給定轉速突變的實驗波形。圖12為突增突減負載時的估算轉速和實際轉速波形。圖9給出了給定轉速為750 r/min時的定子電流，轉子磁鏈，轉子磁鏈角和轉速四個量的估算波形(以A相電流作為參考基準)。可以看出，相位和幅值跟蹤良好。圖10(a)給出了轉速為750 r/min時的滑模觀測器和全階觀測器的估算轉子磁鏈，圖10(b)則給出了兩種觀測器的估算轉子磁鏈角波形。從波形圖10可以看出，兩種觀測器的估算值基本相同，從而證明了該滑模觀測器觀測磁鏈的正確性。圖11為給定轉速由750 r/min突減到150 r/min,后又突增到750 r/min的實驗波形。估測轉速與實際轉速的波形對比表明，轉速的動態性能很好，估算轉速能夠快速準確地跟蹤實際轉速。加減載實驗中定子電流和估測轉速的波形如圖12所示，轉速為750 r/min，負載電流由空載3.08 A增加到5.5 A后又減載為3.08 A。轉速在動態過程中略有超調后又很快恢復到750 r/min。實驗結果驗證了該自適應觀測器轉速觀測的魯棒性。

圖11 給定轉速突變時的實際轉速和估算轉速波形Fig.11 Waveforms of actual speed and estimated speed when the given speed is changed

圖12 突增突減負載時的估算轉速波形Fig.12 Waveform of estimated speed when the load is changed

5 結 論

本文研究了一種估算異步電機的轉子磁鏈和轉速的自適應滑模觀測器。該觀測器在電機靜止坐標系下的狀態方程的數學模型上，利用估算電流和實際電流的誤差構造滑模面，建立了狀態估算方程，從而估算出電機轉子磁鏈。電機轉速通過自適應理論估算。整個觀測器的穩定性由李雅普諾夫穩定性理論保證。該觀測器的方案實現簡單，對參數變化的魯棒性較好。研究表明，該觀測器可以實現對磁鏈和轉速的觀測，并對參數的變化具有較好的魯棒性。仿真結果和實驗波形驗證了該方案的有效性和可行性。

[1] Tursini M, Petrella R, Parasiliti F.Adaptive sliding-mode observer for speed-sensorless control of induction motors[J].IEEE Transactions on Industry Applications, 2000, 36(5):1380-1387.

[2] 陳伯時.電力拖動自動控制系統[M].第3版.北京：機械出版社，2008.

[3] 張永昌,張虎,李正熙.異步電機無速度傳感器高性能控制技術[M].北京：機械工業出版社,2015.

[4] 張永昌,趙爭鳴，張穎超,等.基于全階觀測器的三電平逆變器異步電機無速度傳感器矢量控制系統[J].電工技術學報,2008, 23(11):34-40. ZHANG Yongchang, ZHAO Zhengming, ZHANG Yingchao, et al.Sensorless vector control system of induction motor fed by three-level inverter using a full order observer[J].Transactions of China Electrotechnical Society, 2008, 23(11):34-40.

[5] 尹忠剛,趙昌,鐘彥儒,等.采用抗差擴展卡爾曼濾波器的感應電機轉速估計方法[J].中國電機工程學報, 2012(18):152-159. YIN Zhonggang,ZHAO Chang,ZHONG Yanru, et al.A speed estimation method of induction motors using the robust extended kalman filter[J].Proceedings of the CSEE, 2012(18):152-159.

[6] ZHANG Y,ZHAO Z,LU T,et al.A comparative study of Luenberger observer, sliding mode observer and extended Kalman filter for sensorless vector control of induction motor drives[C]//Energy Conversion Congress and Exposition,IEEE，2009:2466-2473.

[7] 廖永衡,馮曉云,王珍.基于定子磁鏈滑模觀測器的異步電機空間矢量調制直接轉矩控制[J].中國電機工程學報, 2012(18):88-97. LIAO Yongheng, FENG Xiaoyun, WANG Zhen.Induction motor direct torque control based on stator flux sliding mode observer and space vector pulse width modulation[J].Proceedings of the CSEE, 2012(18):88-97.

[8] Sangwongwanich S, Doki S, Yonemoto T, et al.Adaptive sliding observers for direct field-oriented control of induction motor[C]// Industrial Electronics Society, 1990.Proceedings of the 16th Annual Conference on.IEEE,1990:915-920 vol.2.

[9] 王高林，陳偉，楊榮峰,等.無速度傳感器感應電機改進轉子磁鏈觀測器[J].電機與控制學報，2009，13(5)：638-642. WANG Gaolin,CHEN Wei,YANG Rongfeng, et al.Improved rotor flux estimator for sensorless induction motor[J].Electric Machines and Control, 2009，13(5)：638-642.

[10] 路強,沈傳文,季曉隆,等.一種用于感應電機控制的新型滑模速度觀測器研究[J].中國電機工程學報, 2006, 26(18):164-168. LU Qiang,SHEN Chuanwen,JI Xiaolong, et al.A novel sliding-mode observer for speed-sensorless induction motors[J].Proceedings of the CSEE, 2006, 26(18):164-168.

[11] ZHAO L,HUANG J,LIU H,et al.Second-order sliding-mode observer with online parameter identification for sensorless induction motor drives[J].IEEE Transactions on Industrial Electronics, 2014, 61(10):5280-5289.

[12] 趙德宗，張承進，郝蘭英.一種無速度傳感器感應電機魯棒滑模控制策略[J].中國電機工程學報，2006，26(22)：122-127. ZHAO Dezong,ZHANG Chengjin,HAO Lanying.A novel sliding-mode observer for speed-sensorless induction motors[J].Proceedings of the CSEE, 2006, 26(22)：122-127.

[13] Vieira R P, Gastaldini C C, Azzolin R Z,et al.Discrete-time sliding mode speed observer for sensorless control of induction motor drives[J].Iet Electric Power Applications, 2012, 6(9): 681-688.

[14] 鄒伯敏.自動控制理論[M].第3版.北京：機械工業出版社，2007.

[15] 宋文祥,周杰,尹赟.感應電機轉速自適應全階磁鏈觀測器的離散化[J].上海大學學報(自然科學版), 2012,18(6):582-588. SONG Wenxiang,ZHOU Jie,YIN Yun.Discretization of speed adaptive full-order flux observer for induction motors[J].Journal of Shanghai University(Natural Science Edition),2012, 18(6):582-588.

(編輯：邱赫男)

Adaptive sliding mode observer based sensorless control system of induction motor

GAO Yan-xia， CHEN Jing， FAN Ying-peng， SONG Wen-xiang

(School of Mechatronics Engineering and Automation，Shanghai University，Shanghai 200072，China)

For the problem of poor robustness to parameter change of induction motor speed sensorless control, an adaptive sliding mode observer based sensorless vector control method is presented for induction motor in this paper.The rotor flux observer was constructed on the basis of the state equation in static coordinate system.The sliding mode surface of the observer was derived by the error of the estimated stator current and the actual stator current.With the sliding motion, the estimated values were reaching the actual values finally, thus realizing the estimation of the motor rotor flux.The motor speed was obtained by adaptive theory.The Lyapunov stability theory guarantees the stability of the presented observer.Compared with other methods, adaptive sliding mode observer in this paper is superior in implementation easily and better robustness to the motor parameters deviations.The method has been simulated and implemented using the TMS320F2812 fixed-point DSP controller.Simulation and experiment results verify its feasibility and effectiveness, and under the condition of the load disturbance and the given speed change the sliding mode observer has certain robustness.

induction motor; adaptive sliding mode observer ; speed sensorless ;vector control; robustness

2016-05-04

國家自然科學基金(51377102)；國家重大科學儀器設備開發專項資助項目(2012YQ15008703)

高艷霞(1958—)，女，副教授，研究方向為電機驅動控制及應用、電力電子變換； 陳 靜(1991—)，女，碩士研究生，研究方向為異步電機的無速度傳感器控制； 范應鵬(1991—)，男，碩士研究生，研究方向為異步電機的無速度傳感器控制； 宋文祥(1973—)，男，教授，博士生導師，研究方向為電機驅動控制及應用、電力電子變換。

高艷霞

10.15938/j.emc.2017.04.002

TM 343

A

1007-449X(2017)04-0008-09