基于無網格方法的環境溫度對乒乓球運動軌跡影響研究

丁勤衛，李 春，張俊偉，任 杰，施之皓，郝文星

乒乓球作為一項極具觀賞性和競技難度的運動，具有質量輕、速度快、旋轉高以及戰術多變性等特點[1-3]。乒乓球運動已成為我國普遍性運動且具有極為廣泛的群眾基礎，并作為我國國球，繼1996年奧特蘭大奧運會以來已多次包攬奧運會冠軍[2]。國內外學者對于乒乓球做了大量研究[4]，其中多數研究為戰術理論研究[5]、球員打法研究[6-7]以及心理分析、乒乓球管理和教學管理研究[8]。

計算機技術及數值計算發展，為乒乓球運動學及動力學數值仿真提供了技術保證。例如:計算機仿真技術在乒乓球拍的強度研究、乒乓球碰撞研究以及乒乓球運動軌跡預測研究的應用等[9-13]。文獻[9]基于ODE的交互式可視化仿真環境，著重于旋轉球，考慮旋轉過程中受到重力、Magnus升力以及空氣阻力，借鑒網球升阻力系數，不考慮旋轉速度的變化，求解運動方程得到乒乓球運動軌跡，驗證了運動模型的準確性，為揭示乒乓球運動軌跡、乒乓球機器人的發展提供了科學依據。文獻[10]基于模型參數學習和自適應模型的調整的乒乓球運動狀態估計和軌跡預測算法，實驗驗證了算法的實時性和高效性。文獻[11]采用改進的運動學模型的算法，考慮空氣阻力對乒乓球速度的影響，將其速度作為動態反饋參數，結果表明效果準確性，并采用OPENGL的3D仿真平臺直觀分析預測軌跡。A NAKASHIMA等[12]實驗研究了旋轉乒乓球與球拍的碰撞模型，通過水平和垂直方向恢復力系數確定碰撞后乒乓球速度變化，并通過了其他實驗數據驗證碰撞模型和各方向的恢復力系數的可行性。

然而，乒乓球在空氣中運動，實質上是一種流體的繞流過程，空氣的粘性會影響著球體的升力和阻力，進而影響乒乓球的速度、旋轉、軌跡及落點。在上述乒乓球軌跡預測仿真研究中為便于求解或因計算資源限制，多將乒乓球運動過程中的升、阻力系數作為常數以及乒乓球旋轉速度作為定值。顯然這與實際情況存在較大差距。為更加真實地研究乒乓球復雜的氣動流場，OU KUI等[14]采用計算流體力學方法（CFD）對乒乓球軌跡進行數值模擬，得到乒乓球運動軌跡并分析其流場，僅求解了旋轉速度大小及方向對乒乓球軌跡影響。

根據專業教練帶隊經驗以及自身體驗，乒乓球作為球員之間的快速回往復運動，不僅需要考慮乒乓球運動速度及旋轉大小方向對乒乓球運動軌跡的影響，更需要研究環境因素對乒乓球運動軌跡影響。為此必須對乒乓球運動的三維非定常流場開展數值模擬，以便從流動機理角度研究球體不同運動狀態的內在機理。1985年，R D MEHTA[15]提出環境溫度對棒球、足球及網球的運動存在影響，但未涉及乒乓球。顯然，輕而小的乒乓球比棒、足、網球輕得多的乒乓球受溫度影響更大。因此，本文采用無網格格子Boltzmann方法（LBM）數值求解乒乓球三維非定常流場，研究不同溫度對乒乓球運動軌跡的影響，分析乒乓球運動軌跡及運動參數隨時間變化曲線，并且通過乒乓球運動過程中的瞬態流場細微結構得到影響球體運動諸參數的流動機理。

1 乒乓球分析基礎

1.1 乒乓球理論基礎

國際乒聯規定比賽使用乒乓球質量m=2.7 g，半徑為0.02 m，乒乓球桌尺寸分別為:長2.74 m、寬1.525 m、高0.76 m以及網高0.152 5 m[16-17]（見圖1）。

根據乒乓球旋轉所繞旋轉軸不同可分為6大旋轉[18]:上旋、下旋、左旋、右旋、順旋以及逆旋（見圖2）。圖中，ω為乒乓球旋轉角速度，單位是rad/s；v為乒乓球運動速度，單位是m/s。

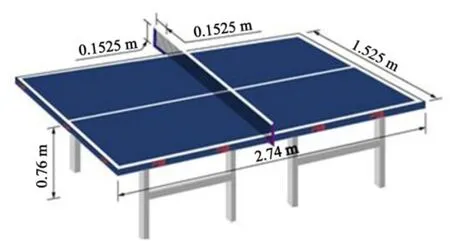
圖1 乒乓球球桌尺寸Figure1 Geometry Parameters of Table

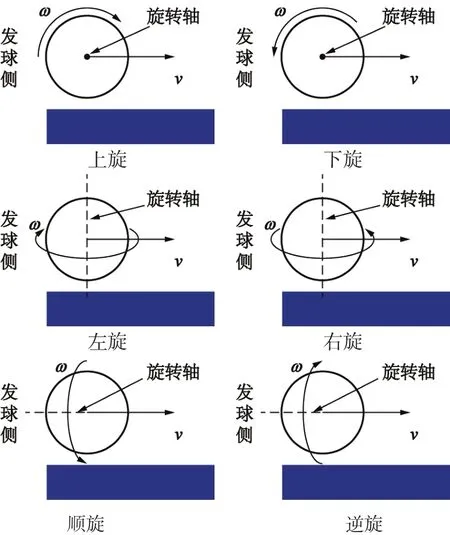
圖2 6大旋轉Figure2 Six Spin

1.2 受力分析

Magnus效應是普遍存在的，在工程各方面都具有重要的作用[19-23]。在粘性流體中，旋轉運動的球體會帶動周圍流體做旋轉運動，當存在繞流時，球體表面將出現壓力差，從而產生作用力即Magnus力。飛行中的乒乓球，自身旋轉導致的Magnus效應可使其偏離原有軌跡。

在乒乓球比賽過程中，對于上旋球在Magnus效應下，乒乓球產生向下的Magnus作用力，對于下旋球則呈現相反的作用，同樣側向球旋轉會導致球體產生側向偏離[1，24]（見圖3）。對于運動過程中的乒乓球，不同旋轉方向因Magnus效應導致不同的軌跡偏離（見圖4），圖中，vx及vy分別為x及y軸方向速度，單位是m/s。

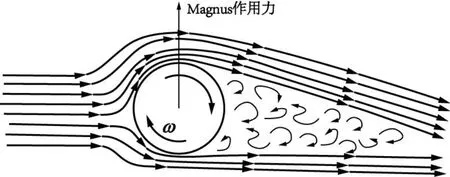
圖3 下旋球Magnus效應Figure3 Magnus Effect of Back Spin

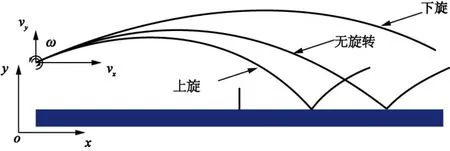
圖4 不同旋轉方向乒乓球運動軌跡Figure4 Trajectory of Table Tennis in Different Spin Direction

乒乓球在運動過程中受到自身重力、空氣阻力以及Magnus力等綜合作用。對不同旋轉方向下乒乓球運動過程進行受力分析（見圖5）。圖中，Fg、FL以及FD分別為自身重力、Magnus力以及空氣阻力。

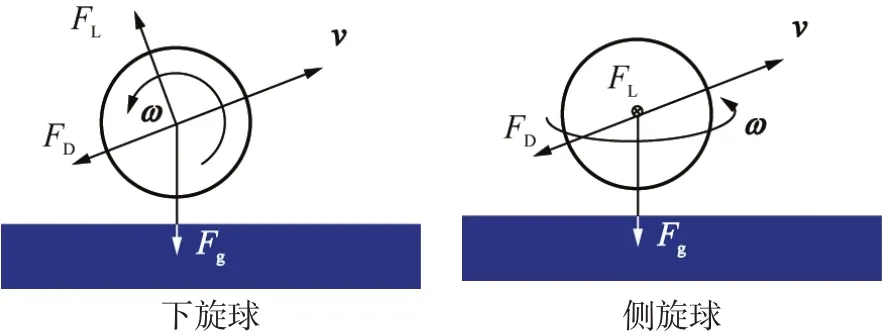
圖5 不同旋轉方向乒乓球受力分析Figure5 Force of Table Tennis in Different Spin Direction

2 計算方法[25]

本文采用基于粒子和具有完整拉格朗日函數的方法對格子Boltzmann-BGK方程和不可壓縮的Navier-Stokes方程進行求解。此方法無需對流體區域進行網格劃分，可較好地體現乒乓球外形特性。對于運動中的乒乓球模擬免去了網格變形的問題，極大地提高了計算的可靠性。計算采用大渦模擬（LES）的方法對乒乓球流場中不同尺度的渦進行處理，對流速梯度較大的區域自動增加粒子數，提高了對乒乓球運動尾渦的捕捉精度。

2.1 格子Boltzmann-BGK方程

格子Boltzmann方法是以介觀動理學模型為基礎的無網格方法，通過求解描述粒子運動方程從而獲得宏觀信息，包括:速度、壓力以及溫度等，方程1為Boltzmann方程:

式中，r為自封閉系統內格子的一個格點；ei為流體第i個粒子的離散速度集合；δt為離散時間步長；t為當前時間步；fi是以速度ei運動的速度分布函數；Si(r,t)為碰撞算子項，表示分子碰撞對速度分布函數的影響。

碰撞算子反映了微觀流體粒子的相互作用，對模型能否準確表示處流體系統的物理規律有著關鍵作用。由于碰撞算子涉及高度非線性積分以及分子間具有耦合作用，因此GROSS等[26]引入方程（2）所示的BGK簡化線性化碰撞算子:

式中，τ稱為松弛時間是平衡態分布函數。

格子Boltzmann-BGK方程是采用BGK線性碰撞算子簡化的Boltzmann方程的一種離散形式，包括空間、速度以及時間的離散[25]。

2.2 基本格子Boltzmann模型

完整的格子Boltzmann模型包含:平衡態分布函數、離散速度模型以及分布函數的演化方程[27]。1992年，QIAN等[28]提出的DdQb系列模型作為格子Boltzmann方法的基本模型，如二維D2Q9[29]及三維D3Q27[30]。本文采用D3Q27模型（見圖6）。

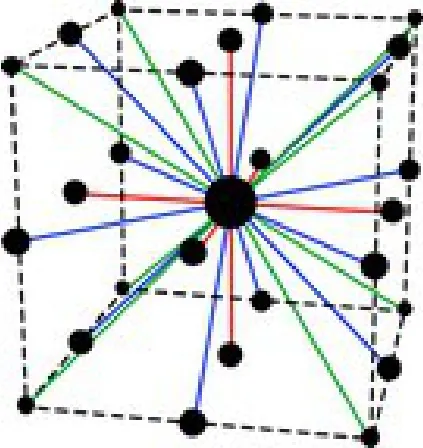
圖6 D3Q27模型Figure6 D3Q27 Model

方程（3）為D3Q27系列模型的平衡態分布函數，方程（4）為其對應的三維離散速度矢量[30]:

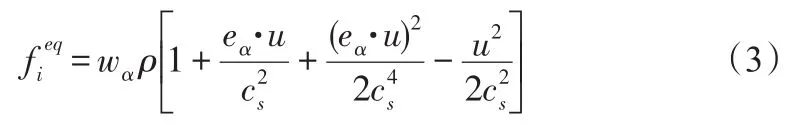
式中，cs為離散系統的聲速；u為宏觀運動速度；wα為權系數，定義為:

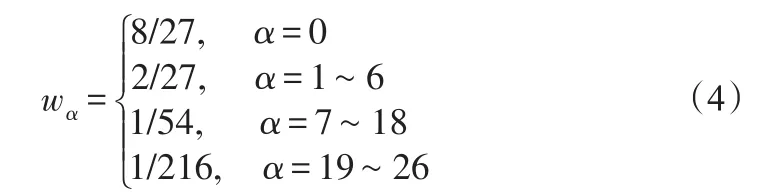
eα為三維離散速度矢量，定義為:

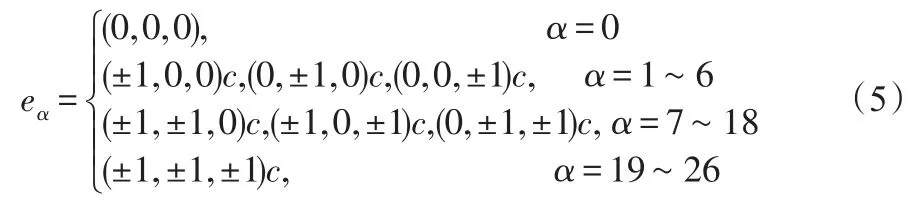
式中:c為離散系統對應的格子速度。

3 參數與建模

圖7為球桌及乒乓球的計算域，其大小為:3.5m×1.5m×2.5m。乒乓球在x軸方向（長度方向）的速度vx=6.0 m/s，在y軸方向（高度方向）的速度vy=1.6 m/s，在z軸方向（寬度方向）vz=0；乒乓球旋轉速度:ωx=ωy=ωz=0 rad/s，乒乓球初始位置（0，0.2，0.7）m。

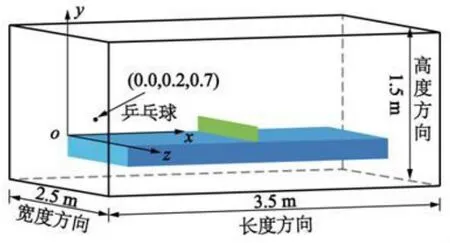
圖7 計算域Figure7 Computational Domain

本文綜合考慮環境溫度變化導致空氣粘性及密度的改變對乒乓球空氣啟動作用的影響，采用格子Boltzmann方法，研究不同環境溫度對乒乓球軌跡影響。圖8為環境溫度對空氣粘性及密度的影響曲線，表1為3種不同溫度時相對應的空氣密度粘度[31]。

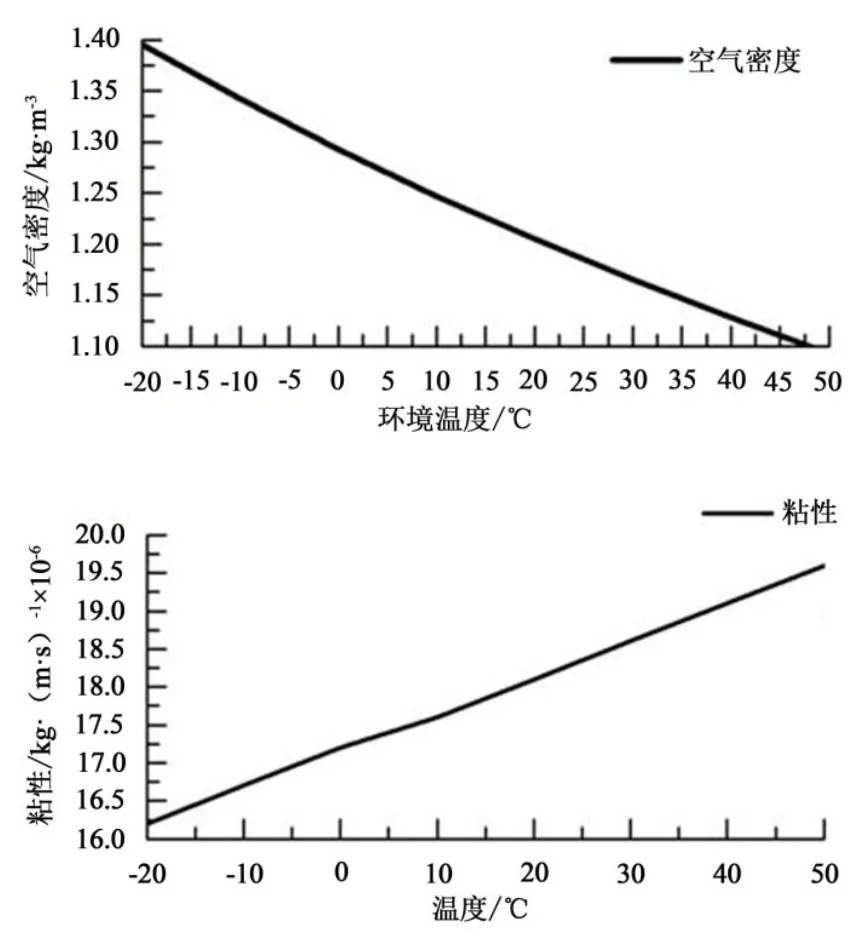
圖8 空氣密度、粘性隨溫度變化Figure8 The Air Density and Viscosity Changes with Temperature

表1 不同環境溫度對應的密度及粘度Table1 The Air Density and Viscosity in Different Temperature

4 結果與分析

圖9為0、15和30℃3種不同情況下的乒乓球運動軌跡圖。圖9（a）和（b）分為xoy和xoz平面軌跡圖，圖9（c）和（d）分別為xoy和xoz平面軌跡局部放大圖。

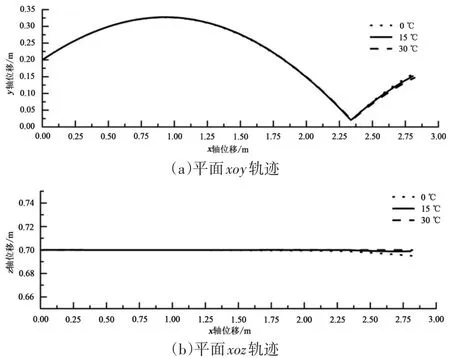
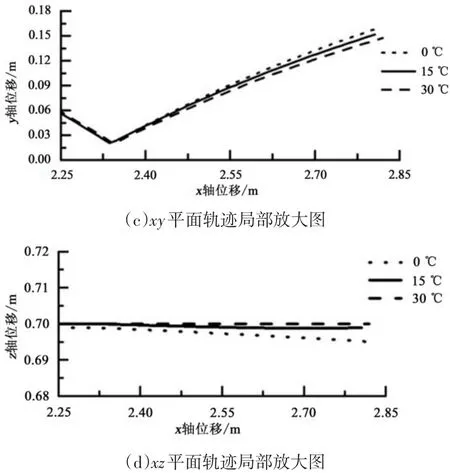
圖9 乒乓球軌跡圖Figure9 Trajectory of Table Tennis

圖9 （a）及圖9（c）可見在軌跡上升段，3種溫度下乒乓球運動軌跡差別很小；在軌跡下降段，3種不同溫度下軌跡出現微小差別；在乒乓球與桌面發生碰撞后，乒乓球軌跡產生較大偏差。乒乓球軌跡隨溫度升高，其最終點越低，分別為:（2.814 17，0.159 83）、（2.805 82，0.151 67）及（2.820 25，0.147 55），以乒乓球半徑為基準，0℃與15℃軌跡x軸方向偏差為41.75%，在y軸方向偏差為40.8%；15℃與30℃軌跡x軸方向偏差為72.15%，在y軸方向偏差為20.6%。

圖9（b）及圖9（d）中可知在軌跡上升段，0、15以及30 ℃在z軸方向沒有明顯的偏轉；但在軌跡下降段，三者相比產生微小的偏差；在與桌面碰撞后，乒乓球軌跡在3種不同溫度情況下產生明顯的偏差，并且隨著乒乓球繼續運動偏轉距離越來越大。乒乓球在z軸方向的偏轉隨著溫度升高而降低，軌跡最終點分別為:（0.159 83，0.695 08）、（0.151 67，0.698 93）及（0.147 55，0.699 9），相對于乒乓球半徑，0℃與15℃軌跡z軸方向偏差為19.53%；15℃與30℃軌跡z軸方向偏差為4.85%。

圖10及圖11表明乒乓球運動速度及旋轉速度在運動過程中隨時間變化，各方向運動速度及旋轉速度變化趨勢相同，但數值有較大的差別。沿x軸方向，即球體前進方向速度因受到空氣阻力作用在運動過程中逐漸減小，與桌面碰撞后速度發生突降；y軸運動速度因重力及Magnus作用力等多重作用力綜合作用在運動過程中先減小后增大，在與桌面碰撞后乒乓球速度方向瞬時發生變化，并產生一定的速度損失；z軸運動速度有較小的變化，與桌面碰撞過程三者速度都發生突變。乒乓球旋轉速度在x及y軸方向有一定變化，并與桌面碰撞后都發生突變。

雖然環境溫度不同乒乓球的運動參數隨時間和空間尺度變化的趨勢基本相同，但隨著時間或飛行距離的變化，尤其是與桌面碰撞反彈后其參數變化有著很大的差異。x軸方向運動速度在軌跡運動過程中3種不同溫度條件下無明顯差別，碰撞后，速度變化產生明顯差別，15℃條件下乒乓球運動速度最小，其他兩者無明顯區別；在y軸方向運動速度碰撞前無明顯差別，碰撞后乒乓球速度隨溫度升高而增大；在z軸方向運動速度因三者空氣粘性阻力不同從而有著巨大的差別，運動速度大小隨著溫度增大而增大，但在碰撞后因碰撞復雜性，三者速度就很大的差別；旋轉速度在時間t=0.15 s之前，在3個方向上不同溫度情況下旋轉速度無明顯差別；旋轉速度在時間t=0.15～0.41 s，3個方向有著巨大的差別，并隨溫度升高而減小；在時間t=0.41 s之后即碰撞后，乒乓球旋轉速度發生突變，x、y軸方向隨溫度增大旋轉速度突變量越小，在z軸方向0℃時其旋轉速度相對于15℃和30℃條件下突變后的旋轉速度較小以及15℃和30℃條件下突變后的旋轉速度無明顯差別。

乒乓球在空氣中運動及與桌面碰撞，其運動軌跡和落點主要受速度和旋轉速度的影響，如較之于15℃和30℃，0℃條件下乒乓球運動參數的變化較大，因此其軌跡相比于其他兩種情況有很大差別；乒乓球碰撞后的運動參數的突變的差別使得乒乓球在不同溫度條件下其軌跡在碰撞之后出現明顯的差別。TANAKAK等[32]實驗研究球體在不同速比SP（SP=ωr/v）下的升力系數CL（CL=2FL/πρr2v2）及阻力系數CD（CD=2FD/πρr2v2），研究結果表明具有不同的速比SP的乒乓球具有不同的升阻力系數；如圖12所示為不同溫度下運動過程中的乒乓球速比隨時間變化曲線。

由圖12可知在同一溫度條件下，不同時刻下，乒乓球運動過程中其速比隨時間發生變化。對于同一時刻下，乒乓球運動過程中速比隨著溫度減小而增大；時間t=0.2 s之前，速比差別小，時間t=0.2 s之后，速比差別大。

乒乓球運動中速度和旋轉速度的變化，與其在不同時刻的瞬態流場密切相關。宏觀上，空氣分子的運動因溫度升高速度加快，使得密度隨溫度升高而減小，粘性隨溫度升高而增大，空氣中運動著的乒乓球的升力和阻力與密度和粘性系數成一定關系。因此，必須得到乒乓球運動中周圍瞬態流場到微觀結構，才能找到流體（空氣）影響其各參數變化的流動機理。圖13、圖14以及圖15分別為15℃條件下不同時刻乒乓球流場渦量、速度云圖以及乒乓球表面壓力圖。

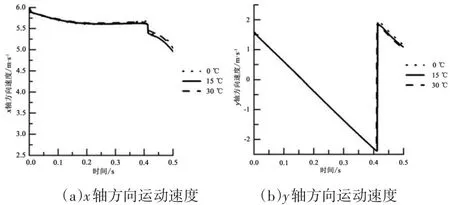
圖10 乒乓球運動過程中速度隨時間變化圖Figure10 Velocity in Movement of Table Tennis

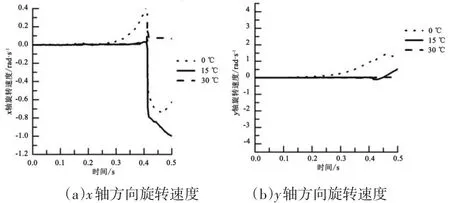
圖11 乒乓球運動過程中旋轉速度隨時間變化圖Figure11 Spin in Movement of Table Tennis

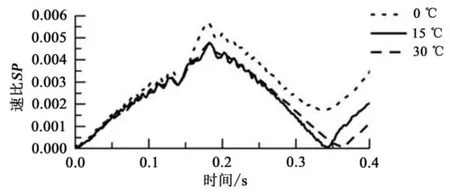
圖12 不同溫度下乒乓球速比SP隨時間變化Figure12 SPChanges with Time in Different Temperature

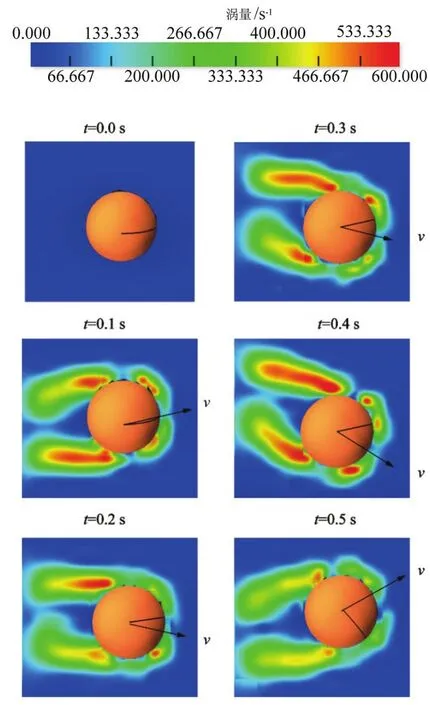
圖13 乒乓球xoy平面渦量場Figure13 Vorticity Field inxoyFace of Table Tennis

圖13 為xoy平面內z軸方向渦量云圖，時間t=0.1～0.4 s為碰撞前，t=0.5 s為碰撞后，圖中給出的速度v表示該時刻乒乓球瞬時速度方向。由圖可見，渦量分布的對稱性取決于球體速度的方向，渦量大小決定運動速度。渦量為速度梯度，直接反應球體周圍的壓力變化。由各時間點的渦量圖可看出，原不具有旋轉作用的乒乓球由于其周圍壓力變化從而受到流場粘性阻力的作用產生了旋轉作用，同時乒乓球運動速度因周圍壓力變化受到流場的作用其產生變化，不同溫度下具有不同的密度和粘性作用使得乒乓球在運動過程中受到流場作用不同，與圖10及圖11所表現出球體在運動過程中不同溫度下運動速度及旋轉速度隨時間變化相吻合。

圖13表明原不具有旋轉的乒乓球由于球體在運動過程中受到流場作粘性阻力作用產生一定的旋轉，導致其上下部分周向速度與球體運動速度方向不同，造成乒乓球速度流場的不對稱性，因此，如圖14時間t=0.1～0.4 s為碰撞前，t=0.5 s為碰撞后，乒乓球因流場不對稱性（關于瞬時速度方向）從而受到流場作用力，不同溫度具有不同的粘性作用，造成這與圖9所表現出不同溫度下球體宏觀軌跡發生變化相吻合。

圖15為不同時刻下乒乓球表面靜態壓力分布，對于初始沒有旋轉的乒乓球在運動過程中其上、下側存在壓力差，且在乒乓球上、下側表面分布不均；乒乓球前、后、上以及下側的表面壓力分布隨著時間的變化產生巨大的變化，表明乒乓球在運動過程中其受到的空氣阻力及升力發生變化的，并與圖12及相關實驗研究相吻合。

不同溫度具有不同的密度以及粘性對乒乓球的作用能在軌跡特別是碰撞后的軌跡中明顯表現出來，20℃和30℃兩者在碰撞后z軸方向旋轉速度突變量相當，但因密度便顯出很大差別進而影響其碰撞后軌跡。在空氣動力粘度方面粘性隨溫度升高而增大，并能在旋轉速度中表現出來:在x軸方向溫度小的即動力粘度小的總是先出現變化的，這也就是0℃運動參數特別其旋轉速度變化相對于15℃和30℃較為提前，而后兩者空氣粘度相對差別不大也就是后兩者變化具有相似性。

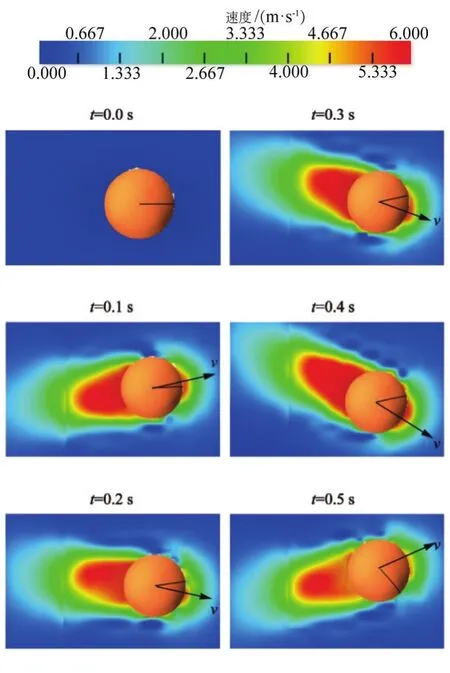
圖14 乒乓球xoy平面速度場Figure14 Velocity Field inxoyFace of Table Tennis

圖15 不同時刻下乒乓球表面壓力圖（xoy平面）Figure15 Pressure in Face of Table Tennis at Different Time（xoy Face）

5 結論與建議

5.1 結論

采用格子Boltzmann方法的數值算法，不同環境溫度對乒乓球運動軌跡的影響，獲取乒乓球運動軌跡、速度及旋轉速度隨時間的變化規律，并分析乒乓球運動過程中速度場、渦量場以及乒乓球表面壓力分布，得到如下結論。

（1）環境溫度影響空氣粘性及密度；乒乓球在運動過程中因空氣粘性作用其旋轉速度及運動速度產生巨大的變化，進而影響運動過程中乒乓球氣動力系數的變化，由乒乓球運動過程中受力分析可知氣動力系數的變化會導致乒乓球在運動過程中受力是發生變化的。因此，運動學方法不能過于簡化運動過程的受力作用，需考慮空氣粘性作用。

（2）不同溫度對乒乓球軌跡存在很大的影響。以乒乓球半徑作為參考，在長度方向上，0℃與15℃偏差為41.75%，15℃與30℃偏差為72.15%；在高度方向，0℃與15℃偏差為40.8%，15℃與30℃偏差為20.6%；在寬度方向，0℃與15℃偏差為19.53%，15℃與30℃偏差為4.85%.

（3）不同溫度對乒乓球運動參數具有很大的影響。0℃條件下其三個方向的運動速度和旋轉速度與15℃和30℃有著很大的差別，而15℃與30℃在個別的方向上或與桌面發生碰撞才產生較大差別。

（4）乒乓球的流場結構及其表面壓力分布隨時間變化，對乒乓球的作用效果與乒乓球運動參數變化及軌跡偏轉相吻合。研究乒乓球運動過程中流場細微結構的變化探究乒乓球流動機理，為乒乓球運動提供一定的理論指導。

5.2 建議

基于以上研究，提出以下建議:（1）乒乓球與桌面碰撞時間短，但碰撞后運動參數運動軌跡都有很大的變化，故球員要具有很敏捷的判斷及擊球反應；（2）就本文乒乓球運動軌跡而言，當環境溫度較高，球員應當對于擊球點做出稍向下移動且稍向右移動的微小動作；當環境溫度較低時，球員應當對擊球點做出稍向上移動且一定的右移動的較小動作。

[1]余萬，李春，朱玲，等.不同比賽氣候條件對乒乓球飛行軌跡影響研究[J].運動，2016，138（10）:23-24.

[2]竇遠行.中國乒乓球隊歷屆奧運戰績:里約第5次包攬金牌[EB/OL].（2016-08-18）[2016-12-17]http://news.sohu.com/20160818/n464841 590.shtml.

[3]曹犇，雷正方.中國乒乓球賽事產業化發展前景規劃[J].西安體育學院學報，2017，34（3）:295-299.

[4]余萬，李春，任杰，等.基于計算流體力學方法的乒乓球軌跡仿真[J].上海體育學院學報，2017，41（3）:89-94.

[5]唐建軍.乒乓球技術學習:理論解釋與實際運用[J].北京體育大學學報，2006，29（2）:259-261.

[6]虞麗娟，張輝，凌培亮.乒乓球比賽技戰術分析的系統研究與應用[J].上海體育學院學報，2008，32（6）:39-43.

[7]魏利婕，史桂蘭.乒乓球削球打法的現狀與持續發展的可行性研究[J].北京體育大學學報，2006，29（12）:1709-1711.

[8]宋亞炳，王偉強，劉建進，等.競賽教學模式在乒乓球選項教學中的實驗研究[J].體育學刊，2014，21（2）:90-94.

[9]楊華，關志明.基于ODE的乒乓球運動軌跡仿真研究[J].計算機仿真，2011，28（9）:230-233.

[10]章逸豐，熊蓉.乒乓球機器人的視覺伺服系統[J].中國科學:信息科學，2012，42（9）:1115-1129.

[11]王奇志，楊曉曉.乒乓球軌跡預測的研究與仿真[J].計算機工程與科學，2013，35（2）:164-169.

[12]NAKASHIMA A，KOBAYASHI Y，OGAMA Y，et al.Modeling of Re?bound Phenomenon between Ball and Racket Rubber with Spinning Ef?fect in ICCAS-SICE 2009-ICROS-SICE International Joint Confer?ence[C].Japan:Fukuoka，2009:2295-2300

[13]MANIN L，POGGI M，HAVARD N.Vibrations of table tennis racket composite wood blades:modeling and experiments[J].Procedia Engi?neering，2012，34（2）:694-699.

[14]KUI OU，Patrice Castonguay，Antony Jameson.Computational Sports Aerodynamics of a Moving Sphere:Simulating a Ping Pong Ball in Free Flight in AIAA Applied Aerodynamics Conference[C].Hawaii:HEHTAulu，2011:1-16.

[15]MEHTA R D.Aerodynamics of sports balls[J].Annual Review of Fluid Mechanics，1985，17（1）:151-189.

[16]THE INTERNATIONAL TABLE TENNIS FEDERATION.ITTF Hand?book 2011/2012[EB/OL].（2011-12-25）[2016-12-17]http://www.ittf.com/ittf_handbook/ittf_hb.html.

[17]THE INTERNATIONAL TABLE TENNIS FEDERATION.ITTF Tech?nical Leaflet T1:The Table[EB/OL].（2013-05-12）[2016-12-17]http://ittf.com/stories/pictures/T1_The_Table_BoD2013.pdf.

[18]王正倫.教你打乒乓球[M].南京:江蘇科學技術出版社，2012.

[19]MEININGER R C.ICAR 101[J].Rock Products，2004，（10）:16-16.

[20]BUTLER AMES.Whirling Spools Lift This Plane[N/OL].https://books.google.com/books?id=xSgDAAAAMBAJ&pg=PA26&dq=Popular+Sci?ence+1931+plane#v=onepage&q&f=false，2016-12-17/1930-09-17

[21]G0TTSCJALK M J.Self-steering axle suspension system having a rota?ry stabilizer:US，US7360773[P]:2008-05-13.http://www.google.com/patents/US7360773

[22]龔志斌，李杰，張輝.旋轉圓柱對翼型氣動性能特性影響的數值模擬研究[J].空氣動力學學報，2015，33（2）:254-258.

[23]陳東陽，LAITH K.ABBS，芮筱亭，等.結構誤差對旋轉穩定彈丸氣動特性影響的數值模擬[J].空氣動力學學報，2014，32（5）:705-710.

[24]SARAFIAN H.Impact of the Drag Force and the Magnus Effect on the Trajectory of a Baseball[J].World Journal of Mechanics，2015，05（4）:49-58.

[25]郭照立.格子Boltzmann方法的原理及應用[M].北京:科學出版社，2009.

[26]BHATNAGAR P L，GROSS E P，KROOK M.A Model for Collision Processes in Gases.I.Small Amplitude Processes in Charged and Neu?tral One-Component Systems[J].Physical Review，1954，94（3）:511-525.

[27]何雅玲，李慶，王勇，等.格子Boltzmann方法的工程熱物理應用[J].科學通報，2009，（18）:2638-2656.

[28]QIAN Y H，D'HUMIERES D，LALLEMAND P.Lattice BGK Models for Navier-Stokes Equation[J].Epl，1992，17（6BIS）:479.

[29]冉政，陳建.關于格子Boltzmann方法的幾個問題（I）[J].空氣動力學學報，2016，34（3）:334-339.

[30]張良奇.格子Boltzmann方法基礎理論研究及其在不可壓縮流動中的應用[D].重慶:重慶大學，2014:15-84.

[31]楊世銘，陶文銓.傳熱學[M].北京:高等教育出版社，2006.

[32]TANAKA K，FUKUIU T，Miyazaki T，et al.Aerodynamic Properties of a Table Tennis Ball[J].Journal of Japan Society of Fluid Mechanics，2014，33（1）:37-45.