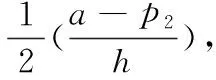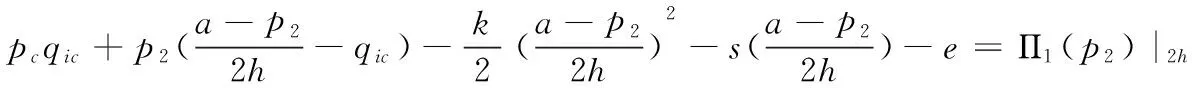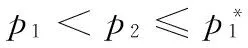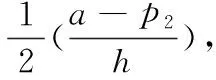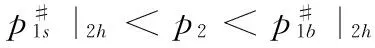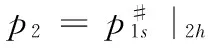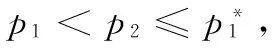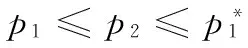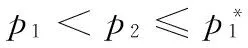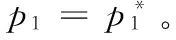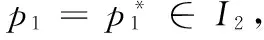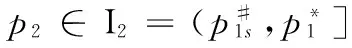差價合約市場力抑制效應的Bertrand博弈模型分析
蒲勇健,孫銜華
(重慶大學經濟與工商管理學院,重慶 400044)
?
差價合約市場力抑制效應的Bertrand博弈模型分析
蒲勇健,孫銜華
(重慶大學經濟與工商管理學院,重慶 400044)
本文通過拓展經典的Bertrand對稱雙寡頭博弈模型,運用勒拿指數測度電力市場絕對電量差價合約對發電商市場力的抑制效應。在發電商二次冪函數成本函數假定下,得到了雙寡頭對稱發電商Bertrand博弈納什均衡的解析表達式,并且發現發電商絕對量差價合約電量的增加會導致發電商均衡狀態勒拿指數的可能取值范圍會下降,因而具有抑制其市場力的效應。本文獲得的拓展Bertrand博弈模型還將經典Bertrand博弈模型加以推廣,得到二次冪函數成本函數條件下存在正均衡利潤Bertrand的充分必要條件,為研究差價合約的其他相關問題提供了工具。
差價合約;勒拿指數;電力市場;伯川德博弈;市場力
1 引言
傳統上電力因被視為自然壟斷行業而一直是各國政府嚴格管制的對象。為了打破壟斷和提高效率,從20世紀80年代開始,各國陸續開始對電力工業進行市場化改革。但在市場成員利益驅動,寡頭壟斷市場結構,以及電力不能大規模儲存等內因以及外因的作用之下,解除管制后的發電商仍具有強大的市場力。市場力的存在會嚴重影響市場有效競爭,從而損害用戶和投資者的利益,甚至引發電力危機。因此針對市場力抑制的研究具有很強的現實價值,對于我國深化電力市場改革,保證市場效率和公平有重要意義。
針對市場力規制措施,國內外學者進行了廣泛研究,主要有增加市場競爭主體,開放需求側市場,簽訂遠期合約,實施價格管制和合理布局電源等措施。其中,購買者和發電公司之間簽訂的差價合約是一種重要的手段。對此有關的文獻大體可以分為四類。一是基于試驗仿真方法分析,通過模擬市場參與者在市場中的可能行為以及包含瓦爾拉斯均衡,納什均衡在內的市場均衡的移動來判定遠期合約對市場力的影響[3-5]。這類研究針對遠期合同,并沒有單獨對差價合約進行研究。二是運用博弈以及均衡理論的市場力分析法,利用博弈理論表明不同類型的差價合約對于發電商市場力的抑制作用。這一類研究利用Cournot或是Bertrand博弈模型進行研究。張洪青和范曉音[6]利用雙發電商的完全信息古諾博弈特殊算例表明絕對電量差價合約可以降低電價,遲正剛[7]認為市場參與者回避價格風險的意圖可作為包括差價合約簽訂實施的動力,其對差價合約的市場力抑制作用進行了定性說明,并提出利用Bertrand以及Cournot模型和勒拿指數分析該問題的分析框架,但未給出任何相關證明,葉澤和喻苗[8]利用雙發電商古諾模型證明了兩階段博弈時差價合約有促進市場競爭的效應。這類研究運用了常見的博弈模型對雙向差價合約的市場力抑制效應進行了研究,但沒有拓展到多廠商的情形。三是通過實證數據研究合約的存在對現貨市場電價的影響。這一類研究多應用在成熟應用差價合約的市場上,如Lucia和Schwartz[9]通過北歐電力市場的數據發現季度遠期合同對現貨市場電價有季節性效應。四是利用供給函數平衡理論SFE(Supply Function Equilibria),如Niu Hui等[10]利用SFE框架下的報價曲線陡度和高度的變化來分析遠期合約的市場力抑制作用。
從理論上看,發電商決策,首先是一個多寡頭競爭博弈,此外,電力作為一種特殊的商品,其具有的不能儲存等特點使得其決策為價格決策,因此應利用Bertrand模型對其進行研究。上述利用博弈理論分析的文獻多集中在經典的Cournot博弈模型,且未拓展到多廠商情形,因此從經濟模型的角度出發存在改進的空間。本文所建立的Bertrand模型,在雙向絕對量差價合約的前提下,即差價合約的合約電量以及合約價格由發電商和購電商共同協商決定,且合約電量為絕對值而非按交易量的固定比例,針對2個寡頭發電商研究差價合約的市場力抑制效應。
與上述基于博弈模型研究的文獻不同(這些模型建立在特殊情形之上或是假設報價參數外生,沒有給出報價參數確定的依據),本文所構建的針對差價合約市場力抑制的理論框架采用經典Bertrand模型并加以拓展,同時采用勒拿指數衡量市場力。本文所建立的針對電力市場的拓展Bertrand模型,針對經典Bertrand模型[11-12]作了如下修改:(1)修改了有關廠商邊際成本(還有平均成本)為常數并且是相同的假定,從而得到具有正利潤的純策略Bertrand博弈模型;(2)模型加入了絕對電量差價合約。同時為了該理論模型更加貼近實際電力市場,文章參考了國內文獻,在模型中借鑒了差價合約在電力市場中的應用分析框架[13-19],考慮了非固定需求量負荷等因素。因此,本文構建了拓展的Bertrand模型,得到其納什均衡表達式,利用其研究了絕對量差價合約電量的變化對于發電量市場力的抑制效應,具有較強的理論意義和現實價值。
2 市場模型與納什均衡
2.1 模型基本假定
1)電力市場中存在2個發電商,它們的成本函數分別為
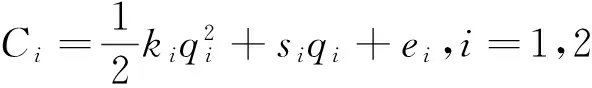
ki≥0,si≥0,ei≥0
(1)
其中Ci,qi,ei分別是第i個發電商的總成本,發電量和固定成本。
2)市場需求曲線
p=a-hQ,a>0,h>0
(2)
其中p,Q分別是市場價格和市場需求電量,a,h是常系數。為了使得下面的分析有意義,假定最高價格高于發電商最低邊際成本,即a>si,i=1,2。
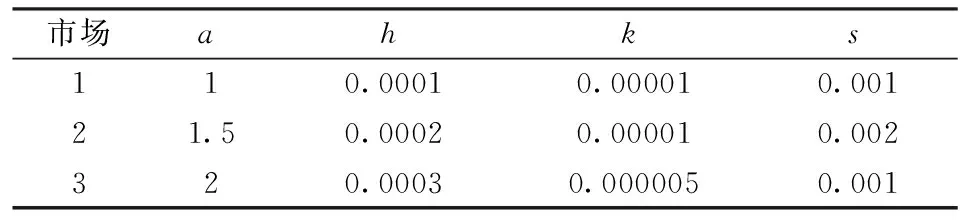
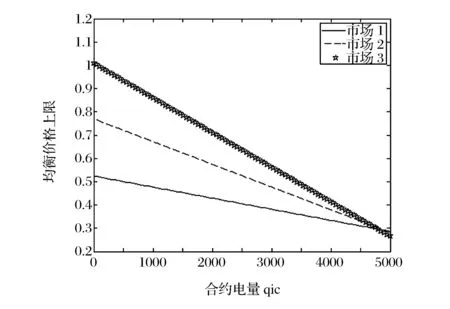
3)文中所考慮差價合約為雙向絕對量差價合約。即企業i與購電方之間簽訂的差價合約規定,如果購電方向企業i(i=1,2)購電量不超過qic,交易價格按照合約規定的固定價格pc執行;超出qic(i=1,2)的購電量以市場價格交易。其中,為保證差價合約有意義,有pc 2.2 完全壟斷廠商利潤函數 定義1假設第i(i=1,…,N)個廠商完全壟斷電力市場,稱此時發電商商i(i=1,2)的利潤與其電價pi之間的數量關系為發電商i(i=1,2)的利潤函數,記為Πi(pi)|ki,si,ei,以下在不引起歧義的情況下簡寫為Πi(pi)。假定發電商i(i=1,2)的支付函數為其獲得的預期利潤。 (3) 最大壟斷利潤的一階條件為: (4) 根據(3),設零利潤價格為p#i(i=1,2),即: Πi(pi)=0 (5) 因此根據(6)可知,發電商i的零利潤價格為: (6) 根據(3),為保證發電商在完全壟斷時的利潤為正,需要假定: (7) 因此,根據(7),(6)式有意義。記: i=1,2 (8) 2.3 最優反應 以下考慮對稱雙寡頭模型,即假定 k1=k2=k,s1=s2=s,e1=e2=e 由于納什均衡是參與人最優反應函數的交集[12]。本節先構建發電商的最優反應函數。 給定發電商2的純策略即價格p2,發電商1的最優反應是發電商1的最優價格。最優反應函數一般是集值函數,即可能有多個最優價格,它們構成一個最優反應集(也可以是空集)。因此最優反應函數是一種映射或者集值函數。 下面將發電商2的策略(p2)分別置于不同的三個區間來求解發電商1的最優反應策略集。這三個區間分別為: 定理1 如果p2∈I1,發電商1的最優反應策略集為: 3)其他情形下,發電商1的最優反應策略是p1>p2。 證明見附錄A。 定理2 如果p2∈I2,則發電商1的最優反應策略是p1=p2,當且僅當π1=Π1(p2)|2h,k1,s1,e1≥Π1(p2)。 證明見附錄B。 定理3 2.4 納什均衡 根據不同情形的最優反應函數交集,納什均衡只可能是前面的兩種情形,并且要求下面的條件成立: 2)π1=Π1(p2)|2h,k,s,e≥Π1(p2),p2∈I2 并且,如果要求均衡利潤大于零,則在上述兩種情形里面都進一步要求有 所有的納什均衡都滿足p1=p2。 證明見附錄C。 由于所有的納什均衡都滿足p1=p2,即不可能存在單一廠商完全壟斷市場的均衡。 記發電商完全壟斷利潤函數非負的價格區間為 D=[p#1s|2h,p#1b|2h] 在p2∈I1存在非負利潤的均衡條件是: I1∩D非空,即下面的條件成立: 根據(4)和(8),該條件為: p2∈I2存在正利潤的均衡條件是: 因為a-p2>0 (9) 是在p2∈I2存在正利潤的充分必要條件。 根據(4)和(8),考察下面不等式成立的 可能性: (10) (10)是可能成立的。 如果h充分大(給定其他參數不變),(10)就成立。在這些場合,在p2∈I2存在正利潤的均衡。這說明,存在使得(9)成立的條件。這樣在p2∈I2就存在正利潤的均衡。 繼而,根據納什均衡,對稱雙寡頭發電商Bertrand模型純策略均衡利潤為非負和正數的條件可由定理4給出。 定理4 對稱雙寡頭發電商Bertrand博弈僅當k=e=qic=0,i=1,2以外的情形,才可能存在正利潤的, 如果存在正的均衡利潤,帶來正均衡利潤的均衡必定是p1=p2∈I2的情形。且在p2∈I2存在正利潤的充分必要條件為式(11)。 (11) 證明見附錄D。 考慮可能的均衡狀態,均衡價格p1=p2=pN qi∈[qs,qb],i=1,2 (12) 其中,式(12)表示發電市場中的安全不等式約束,包括機組的處理上下限、線路傳輸容量極限等約束條件[20-21],其中qs,qb為常數。 假設均衡價格滿足下式: pi∈[a-2hqb,a-2hqs] (13) 根據(4) 此時I2的上限隨著差價合約電量的上升而下降。因為I2的上限也正是所有納什均衡價格的上限,因此存在抑制均衡價格的效應。 勒拿指數為 (12) 由于差價合約電量qic(i=1,2)的增加會導致均衡價格的上限下移,因此抑制均衡價格,從而也有抑制勒拿指數的效應。 由于可能存在多重納什均衡,在這里分析勒拿指數的抑制效應只能夠從這種意義上進行,因為難以判斷由于差價合約電量qic(i=1,2)的增加如何影響均衡的移動。 上節指出在對稱雙寡頭發電商的電力市場中,在拓展Bertrand博弈納什均衡中,每一個發電商的差價合約電量越大,其勒拿指數上限會下移,因而差價合約電量的增加有抑制市場力量的作用。為了更好地說明絕對量差價合約的市場力抑制作用,本節給出一個算例來驗證這個結論。雙寡頭發電商的數據如表1所示。 表1 雙寡頭發電商的各個參數數據 根據(4)可知,可得到圖1和圖2。圖1表示了均衡價格上限的移動,圖2表示了勒拿指數的移動。其中,均衡價格單位為元/KWh,合約電量單位為KWh。由圖1和圖2可以看出,均衡價格上限與絕對量差價合約電量呈負相關關系,勒拿指數上限隨著合約電量增加而下降。因此,上節的結論在這里得到了更好的說明,即在對稱雙寡頭電力市場中,絕對量差價合約電量的增加會抑制發電商的均衡價格,進而抑制市場力。 圖1 均衡價格上限與絕對量合約電量的關系圖 圖2 勒拿指數上限與絕對量合約電量的關系圖 本文通過將經典的Bertrand拓展到非常數 邊際成本的二次冪函數情形,發現存在正均衡利潤的可能性,并導出了出現正均衡利潤的一個充分必要條件。然后運用該拓展Bertrand分析了相對電量差價合約對于發電商市場力量的抑制效應,發現相對電量差價合約存在對于發電商市場力的抑制效應,因為均衡價格存在區間的上限在相對電量差價合約電量增加時下降了,同時也導致勒拿指數分布區間下移。本文的研究限于對稱雙寡頭博弈的情形,結論在非對稱和多發電商的情形可以進行類似的推廣,只不過在數學上更加復雜而已。 附錄A定理1的證明:為得到p2∈I1時發電商1的最優反應策略集,需分情況討論 時的完全壟斷發電商的利潤函數。 2)當p#1s|2h 3)當p2=p#1s|2h或者p2=p#1b|2h發電商1的最優反應策略是p1≥p2 其他情形發電商1的最優反應策略是p1>p2,證畢。 當p1>p2,發電商1的利潤為零,也存在占優其的其他價格策略,所以不是最優策略。只有當p1=p2,π1=Π1(p2)|2h,k1,s1,e1≥Π1(p2)達到發電商1的最大利潤,所以此時發電商1的最優反應策略是p1=p2,證畢。 附錄C納什均衡的證明:下面將發電商2的策略(p2)分別置于不同的三個區間來求解發電商1的最優反應策略集。這三個區間分別為: 其中Π1(p2)|2h表示需求曲線為p=a-2h(q1+q2)時的完全壟斷發電商的利潤函數。 其他情形發電商1的最優反應策略是p1>p2。 當p1>p2,發電商1的利潤為零,也存在占優其的其他價格策略,所以不是最優策略。只有當p1=p2,π1=Π1(p2)|2h,k1,s1,e1≥Π1(p2)達到發電商1的最大利潤,所以此時發電商1的最優反應策略是p1=p2。 納什均衡是所有參與人的最優反應函數的交集。 此時,根據不同情形的最優反應函數交集如下: 1)p2∈I1,注意到此時發電商1的最優反應價格都滿足p1≥p2,在對稱條件下,顯然一定有p1≤p2,所以有p1=p2,因此有前提條件: p#1s|2h≤p2≤p#1b|2h 僅在該條件滿足時才存在均衡。 2)p2∈I2,注意到此時如果有納什均衡,則一定有 p1=p2 并且此時有 π1=Π1(p2)|2h,k,s,e≥Π1(p2) 附錄D定理4的證明: 由于所有的納什均衡都滿足p1=p2,即不可能存在單一廠商完全壟斷市場的均衡。 記發電商完全壟斷利潤函數非負的價格區間為 在p2∈I1存在非負利潤的均衡條件是: I1∩D非空,即下面的條件成立: 根據(4)和(8),該條件為: p2∈I2存在正利潤的均衡條件是: 因為a-p2>0 (13) 是在p2∈I2存在正利潤的充分必要條件。 根據(4)和(8),考察下面不等式成立的可能性: (14) (14)是可能成立的。 如果h充分大(給定其他參數不變),(14)就成立。在這些場合,在p2∈I2存在正利潤的均衡。這說明,存在使得(13)成立的條件。這樣在p2∈I2就存在正利潤的均衡。 [1] 張集. 電力市場的市場力規制理論及應用研究[D]. 北京: 華北電力大學,2007. [2]DavidAK,WenFS.Marketpowerinelectricitysupply[J].IEEETransactionsonEnergyConversion,2001,16(4):352-360. [3]BrandtsJ,Pezanis-ChristouP,SchramA.Competitionwithforwardcontracts:Alaboratoryanalysismotivatedbyelectricitymarketdesign[J].TheEconomicJournal,2008,118 (1):192-214. [4]SmithVL.Anexperimentalstudyofcompetitivemarketbehavior[J].JournalofPoliticalEconomy,1962,70(2):111-137. [5]BowerJ,BunnD.Experimentalanalysisoftheefficiencyofuni-formpriceversusdiscriminatoryauctionsintheEnglandandWaleselectricitymarket[J].JournalofEconomicDynamics&Control,2001,25(3-4):561-592. [6] 張洪青,范曉音. 電力市場中差價合約策略的博弈論分析[J]. 華北電力大學學報(社會科學版), 2008,(5): 11-14. [7] 遲正剛. 單邊開放電力市場的穩定性分析及對策[J]. 電力系統自動化,2002,26(11):5-8. [8] 葉澤,喻苗. 電力市場中差價合約的合謀效應[J]. 長沙理工大學學報(社會科學版),2006,21(3):67-70. [9]LuciaJJ,SchwartzES.Electricitypricesandpowerderivatives:EvidencefromtheNordicpowerexchange[J].ReviewofDerivativesResearch, 2002, 5(1): 5-50. [10]NiuHui,BaldickB,ZhuGuidong.Supplyfunctionequilibriumbiddingstrategieswithfixedforwardcontracts[J].IEEETransactiononPowerSystems,2005,20(4):1859-1867. [11] 蒲勇健. 簡明博弈論教程[M].北京:中國人民大學出版社,2013. [12] 趙耀華,蒲勇健.博弈論與經濟模型[M].北京:中國人民大學出版社,2010. [13] 張新華,葉澤. 考慮價格限制與差價合約的發電容量投資分析[J]. 系統工程理論與實踐,2014,34(9):2220-2227. [14] 李莉,譚忠富,李寧.煤電差價合約及其合作效益優化分配的博弈模型[J]. 中國管理科學,2010,18(4):133-139. [15] 陳曉林,劉俊勇,宋永華,等. 利用差價合同和金融輸電權的組合規避電力市場風險[J]. 中國電機工程學報,25(10):75-81. [16] 張新華,賴明勇,葉澤. 寡頭發電商投資閾值與容量選擇模型及其分析[J]. 中國管理科學,2010,18(5): 106-111. [17] 朱峰. 對沖在電力交易中降低市場經營風險的模擬計算[J]. 中國電機工程學報,2007,27(34):76-83. [18] 馬新順,劉建新,文福拴,等. 計及風險并考慮差價合約的發電公司報價策略研究[J].華北電力大學學報,2005,32(1):37-41. [19]NamYW,YoonYT,DonH,etal.Effectsoflong-termcontractsonfirmsexercisingmarketpowerintransmissionconstrainedelectricitymarket[J].Electricpowersystemsresearch,2006,76(6-7):435-444. [20]EliaE,MaioranoA,SongYH,etal.Novelmethodologyforsimulationstudiesofstrategicbehaviorofelectricityproducers[C]//ProceedingsofthePowerEngineeringSocietySummerMeeting,SeattleJuly16-20,2000. [21] 方陳,李瑞慶,夏清,等. 地區間電力市場互聯互通相關問題(二)基于雙向差價合約的互聯互通市場的納什均衡分析[J]. 電力系統自動化,2009,33(23):42-47. ABertrandModelbasedonContractsforDifferenceforInhibitingMarketPower PUYong-jian,SUNXian-hua (School of Economics and Business Administration, Chongqing University, Chongqing 400044, China) In this paper, the market power inhibiting effects of contracts for differences are studied. Due to oligopolistic characters owned by the electricity market, it is of great importance to focus on methods that could help restricting the market power of generators. The contract for differences is considered an effective way to control market power according to former researches, but the model we propose has the following characters that make our research special and creative. First of all, it is based on Bertrand model, which is properly applied in the electricity market, without adding any exogenous factors suggesting the relationship between the bidding price and the electricity quantity. It provides conditions that guarantee positive profit of generators. Secondly, Lerner index is introduced to the model for assessing market power. The main parts of this paper include the Nash equilibrium of generators in an identical duopoly electricity market (which is gained by analyzing the best responses of each generator), the superior limit of both equilibrium price and Lerner index, the conditions to guarantee positive profit and illustration of identical duopoly electricity market by data simulation. Finally, the conclusion that the absolute electric quantity contract for difference has inhibiting effect on market power in an identical duopoly electricity market is drawn through the movement of the superior limit of Lerner index. This research provides a tool for other researches that consider using Bertrand model for analyzing contractual problems in electricity market, which is not often used in former researches due to the zero profit of classical Bertrand model, though it actually matches the electricity market. contract for difference;Lerner index;electricity market;Bertrand game;market power 1003-207(2017)05-0109-07 10.16381/j.cnki.issn1003-207x.2017.05.013 2015-07-13; 2015-12-22 重慶市“兩江學者”計劃專項經費資助項目; 重慶大學人文社科重點基地創新研究項目(106112015CDJSK02JD04) 蒲勇健(1961-), 男(漢族), 重慶渝中人,重慶大學經濟與工商管理學院, 教授, 博士生導師, 研究方向:能源經濟學、博弈論及數理經濟學,E-mail:puyjan@sina.com. F224.9 A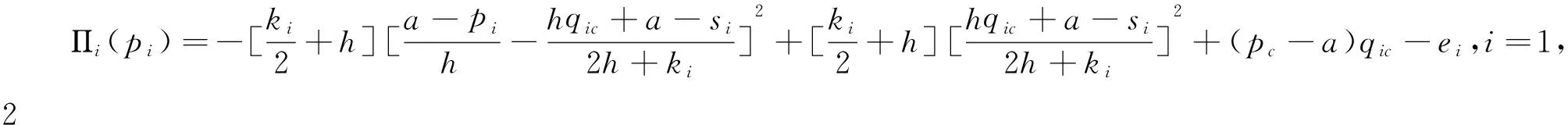

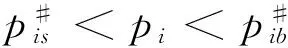
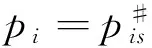
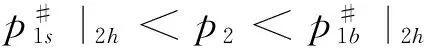

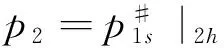
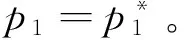
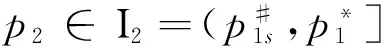
3 均衡狀態的勒拿指數上限

4 算例

5 結語