一種強兼容性的灰色通用預(yù)測模型及其性質(zhì)研究

曾 波，劉思峰，曲學(xué)鑫

(1.重慶工商大學(xué)商務(wù)策劃學(xué)院，重慶 400067; 2.南京航空航天大學(xué)經(jīng)濟與管理學(xué)院，江蘇 南京 210016; 3.重慶工商大學(xué)國家智能制造服務(wù)國際科技合作基地，重慶 400067)

?

一種強兼容性的灰色通用預(yù)測模型及其性質(zhì)研究

曾 波1，劉思峰2，曲學(xué)鑫3

(1.重慶工商大學(xué)商務(wù)策劃學(xué)院，重慶 400067; 2.南京航空航天大學(xué)經(jīng)濟與管理學(xué)院，江蘇 南京 210016; 3.重慶工商大學(xué)國家智能制造服務(wù)國際科技合作基地，重慶 400067)

預(yù)測建模對象的復(fù)雜性導(dǎo)致了灰色模型形式的多樣性與結(jié)構(gòu)的互不兼容性，通過在灰色模型中引入因變量滯后項、線性修正項及常數(shù)修正項，構(gòu)建了一種強兼容性的灰色通用預(yù)測模型(CGPM)，證明了CGPM模型與多變量GM(1, N)模型與GM(0, N)模型及單變量GM(1, 1)模型、DGM(1, 1)模型及NDGM(1, 1)模型的轉(zhuǎn)換條件與等價性質(zhì)，最后通過實例對CGPM模型的有效性進行了驗證；研究成果對優(yōu)化灰色模型結(jié)構(gòu)、提高灰色模型通用性與普適性具有積極意義。

灰色理論；預(yù)測模型；強兼容性；模型轉(zhuǎn)換

1 引言

長期以來，定量預(yù)測研究方法一直為以大樣本數(shù)據(jù)為基礎(chǔ)的數(shù)理統(tǒng)計方法所主導(dǎo)，為了解決“小數(shù)據(jù)、不確定性”系統(tǒng)的分析、預(yù)測、決策與控制問題，上世紀(jì)80年代初，華中工學(xué)院鄧聚龍教授提出了面向“小樣本、貧信息”系統(tǒng)的灰色理論[1]，該理論依據(jù)信息覆蓋，通過序列生成和灰色模型探索事物運動的現(xiàn)實規(guī)律，其特點是“少數(shù)據(jù)建模”。其中，灰色預(yù)測模型是灰色理論的重要組成部分，經(jīng)過三十多年的發(fā)展，它已在農(nóng)業(yè)、工業(yè)、社會、經(jīng)濟、交通、能源、醫(yī)療等眾多領(lǐng)域得到了廣泛地應(yīng)用，成功地解決了生產(chǎn)、科研、管理中的大量重要問題，在該過程中，灰色模型也由原始的GM(1,1)模型擴展出GM(1,N)、GM(0,N)、GM(2,1)、DGM(1,1)、NDGM(1,1)、GM(1,1)冪模型等多種新的預(yù)測模型類別；預(yù)測對象也拓展到數(shù)列預(yù)測、區(qū)間預(yù)測、灰色災(zāi)變預(yù)測、波形預(yù)測、系統(tǒng)預(yù)測[2-3]等。

為了提高灰色預(yù)測模型的模擬與預(yù)測性能，研究人員從初始值[4-5]、背景值[6-7]、光滑度[8-9]、建模對象[10-13]、建模機理[14-18]、模型性質(zhì)[19-21]、模型組合[22]等角度對灰色預(yù)測模型進行了大量深入系統(tǒng)研究，推動了灰色預(yù)測模型理論體系的發(fā)展和完善。然而，由于不同灰色預(yù)測模型通常具有不同的模型結(jié)構(gòu)、建模條件與適用范圍，導(dǎo)致現(xiàn)有灰色模型之間的兼容性較差，然而現(xiàn)實世界的復(fù)雜性導(dǎo)致很多情況下建模對象并不完全滿足某一類模型的建模條件，而是同時兼具多個模型的對象特征，需要通過模型整合才能實現(xiàn)對復(fù)雜系統(tǒng)的客觀模擬，在這樣的情況下如何實現(xiàn)模型結(jié)構(gòu)的集成與兼容是值得深入研究的一個重要內(nèi)容。

本文通過在灰色模型中引入因變量滯后值、線性修正項及常數(shù)修正項，構(gòu)建了一種強兼容性的灰色通用預(yù)測模型(CGPM)，該模型可以通過參數(shù)變化實現(xiàn)與GM(1,N)模型、GM(0,N)模型、GM(1,1)模型、DGM(1,1)模型及NDGM(1,1)模型的等價轉(zhuǎn)換，從理論上證明了CGPM模型能實現(xiàn)對單變量序列與多變量序列的完全兼容；同時由于CGPM模型還可以轉(zhuǎn)化為DGM(1,1)模型及NDGM(1,1)模型，因此CGPM模型同樣可以實現(xiàn)對齊次及非齊次指數(shù)序列的無偏模擬。CGPM模型結(jié)構(gòu)基于不同建模對象的動態(tài)調(diào)整能力，解決了傳統(tǒng)主流灰色預(yù)測模型之間的兼容性問題，對提高灰色模型通用性與普適性具有積極意義。換言之，在運用CGPM模型解決實際管理預(yù)測問題的過程中，不需要首先分析建模數(shù)據(jù)序列的齊次或非齊次指數(shù)特征，也不必考慮因變量序列(系統(tǒng)特征序列)受到何種因素的影響，CGPM模型憑借其強大的兼容能力，能夠根據(jù)建模序列的數(shù)據(jù)特征進而實現(xiàn)其模型結(jié)構(gòu)的動態(tài)優(yōu)化，從而實現(xiàn)對預(yù)測對象的有效模擬及科學(xué)預(yù)測。

2 預(yù)備知識

定義1[2]. 設(shè)X(0)為1-等時距非負(fù)原始數(shù)據(jù)序列：

X(0)=(x(0)(1),x(0)(2),…,x(0)(m))

其中x(0)(k)≥0，D為序列算子，

X(0)D=(x(0)(1)d,x(0)(2)d,…,x(0)(m)d)

X(0)D=X(1)=(x(1)(1),x(1)(2),…,x(1)(m))

X(0)Dr=X(r)=(x(r)(1),x(r)(2),…,x(r)(m))

可見定義1中的變量r代表序列的累加次數(shù)，當(dāng)r=0表示該序列為原始序列，當(dāng)r=1則表示該序列為1次累加生成序列，以此類推。

定義2[2]. 設(shè)序列X(0)、X(1)如定義1所示，則稱序列Z(1)為X(1)的緊鄰均值生成序列：

Z(1)=(z(1)(2),z(1)(3),…,z(1)(m))

其中z(1)(k)=0.5×(x(1)(k)+x(1)(k-1))，k=2,3,…,m。

定義3[2]. 設(shè)序列X(0)、X(1)及Z(1)分別如定義1及定義2所示，則稱：

x(0)(k)+az(1)(k)=b

為含一個變量的一階方程灰色系統(tǒng)預(yù)測模型，簡稱GM(1,1)模型。

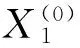
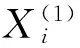
則稱：

(1)

為含N個變量的零階方程灰色系統(tǒng)預(yù)測模型，簡稱GM(0,N)模型。稱：

(2)

為含N個變量的一階方程灰色系統(tǒng)預(yù)測模型，簡稱GM(1,N)模型。

注：在以往關(guān)于多變量灰色系統(tǒng)預(yù)測模型的定義中，通常用N表示變量個數(shù)，而用n表示序列中元素個數(shù)。本文為避免混淆，用字母m代替n表示序列中元素個數(shù)，從而確保對GM(0,N)及GM(1,N)模型的定義更清晰準(zhǔn)確。

定義5[12]. 設(shè)序列X(0)及X(1)如定義1所示，則稱：

x(1)(k+1)=β1x(1)(k)+β2

為GM(1,1)模型的離散形式，或離散GM(1,1)模型，簡稱DGM(1,1)模型。

定義6[2]. 設(shè)序列X(0)及X(1)如定義1所示，則稱：

x(1)(k+1)=β1x(1)(k)+β2k+β3

為近似非齊次指數(shù)離散灰色模型，簡稱NDGM(1,1)模型。

3 模型構(gòu)建與模型性質(zhì)

(3)

P=(BTB)-1BTY

(4)

其中B,Y分別為：B=

根據(jù)定義1，可知CGPM模型的還原式為

(5)

性質(zhì)1：GM(1,N)模型及CGPM模型分別如定義4及定義7所述，則當(dāng)h1≠0，h2=0，h3=0且N>1時，CGPM模型即為GM(1,N)模型。

證明：根據(jù)公式(3)可知， 當(dāng)h2=0且h3=0時

(6)

公式(6)可變形為：

(7)

令h1=(1-0.5a)/(1+0.5a)，則公式(7)可進一步變形為：

(8)

整理公式(8)可得，

(9)

根據(jù)定義1可知，

(10)

(11)

將公式(10)及公式(11)代入公式(9)，可得：

(12)

公式(12)中，a及bt(t=2,3,…N)均為常數(shù)，令ct=bt/(1+0.5a)，則公式(12)可簡化為：

(13)

公式(13)即為含N個變量的一階方程灰色預(yù)測模型，即GM(1,N)模型。 證明結(jié)束。

性質(zhì)2：GM(0,N)模型及CGPM模型分別如定義4及定義7所述，則當(dāng)N>1，h1=0且h2=0時，CGPM模型即為GM(0,N)模型。

證明: 當(dāng)N>1，h1=0且h2=0時，根據(jù)公式(3)可知：

(14)

公式(14)即為含N個變量的零階方程灰色預(yù)測模型，即GM(0,N)模型。 證明結(jié)束。

性質(zhì)3：GM(1,1)模型及CGPM模型分別如定義3及定義7所述，則當(dāng)h2=0，h1·h3≠0且N=1時，CGPM模型即為傳統(tǒng)的GM(1,1)模型。

證明: 根據(jù)公式(3)可知，當(dāng)h2=0，h1≠0，h3≠0且N=1時：

(15)

令h1=(1-0.5a)/(1+0.5a)，則公式(15)可進一步變形為：

(16)

整理公式(16)，可得：

(17)

根據(jù)定義1及定義2，公式(17)可變形為：

(18)

其中b=(1+0.5a)h3，公式(18)即為單變量1階方程灰色模型，即GM(1,1)模型。

證明結(jié)束。

性質(zhì)4：DGM(1,1)模型及CGPM模型分別如定義5及定義7所述，則當(dāng)h1·h3≠0，h2=0且N=1時，CGPM模型即為DGM(1,1)模型。

證明：當(dāng)h1·h3≠0，h2=0且N=1時，根據(jù)定義7可知，

(19)

在上式中，h1及h3均為常數(shù)，令β1=h1，β2=h3則公式(19)變形為：

x(1)(k)=β1x(1)(k-1)+β2

(20)

公式(20)即為DGM(1,1)模型。證明結(jié)束。

性質(zhì)5：NDGM(1,1)模型及CGPM模型分別如定義6及定義7所述，則當(dāng)h1·h2·h3≠0且N=1時，CGPM模型即為NDGM(1,1)模型。

證明：當(dāng)h1·h2·h3≠0且N=1時，根據(jù)定義7可知，

(21)

公式(21)可變形為：

(22)

在上式中，h1、h2及h3均為常數(shù)，令β1=h1，β2=h2，β3=h3-h2，則公式(22)變形為：

x(1)(k+1)=β1x(1)(k)+β2k+β3

(23)

公式(23)即為NDGM(1,1)模型。 證明結(jié)束。

根據(jù)性質(zhì)5，可以進一步得到如下推論。

推論1：CGPM模型定義7所述，則當(dāng)h1·h2·h3≠0且N=1時，CGPM模型能實現(xiàn)對齊次指數(shù)序列及非齊次指數(shù)序列的無偏模擬。

推論2：CGPM模型定義7所述，則當(dāng)h1·h2·h3≠0且N=1時，CGPM模型能實現(xiàn)對線性函數(shù)序列的無偏模擬。

推論1及推論2可通過矩陣運算或克萊姆法則來加以證明，此處略。

根據(jù)CGPM模型的上述性質(zhì)，可得CGPM模型與其他模型之間拓展關(guān)系，如圖1所示。

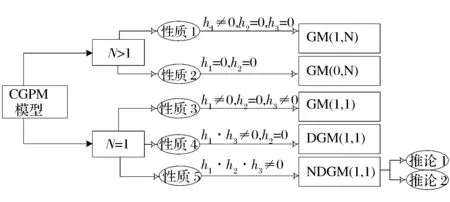
圖1 CGPM模型與其他模型的拓展關(guān)系示意圖

從圖1中可以看出，CGPM模型可以通過模型參數(shù)的變化實現(xiàn)與多變量GM(1,N)模型、GM(0,N)模型及單變量GM(1, 1)模型、DGM(1, 1)模型及NDGM(1, 1)模型的轉(zhuǎn)換，表明CGPM模型更具兼容性、通用性與泛化能力。

4 模型比較分析

從表2可以看出，CGPM模型可以實現(xiàn)對單變量序列的模擬，且其模擬性能優(yōu)于經(jīng)典的GM(1,1)模型，再次說明CGPM具有較強的模擬能力。

表1 GM(0,2)模型與CGPM模型對多變量序列的模擬值與模擬誤差

表2 GM(1,1)模型與CGPM模型對單變量序列的模擬值與模擬誤差

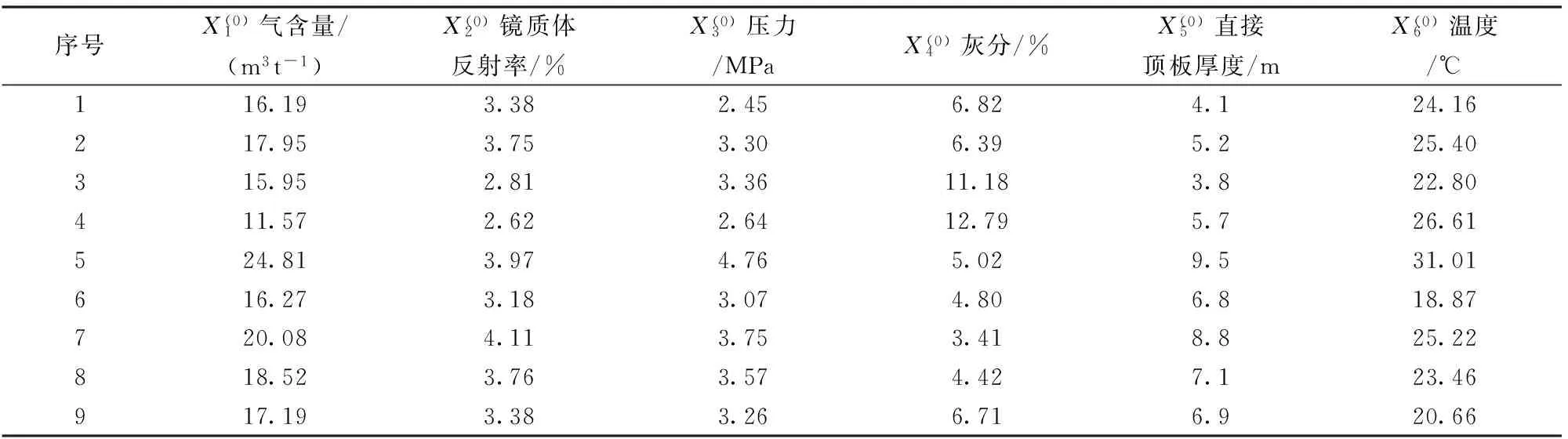
表3 沁水煤田晉城礦區(qū)3號煤層參數(shù)統(tǒng)計表

(a)CGPM模型

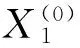
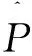
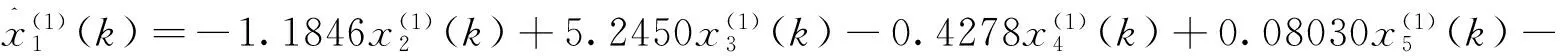
(24)

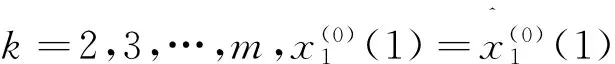
(b)GM(0,6)模型

系統(tǒng)特征序列的GM(0,6)模型為：

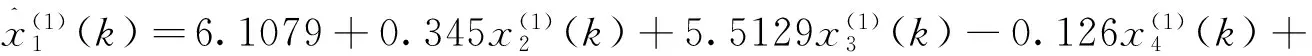
(25)

CGPM模型及GM(0,6)模型的模擬結(jié)果如表4所示。

5 結(jié)語

由于不同灰色預(yù)測模型通常具有不同的模型結(jié)構(gòu)、建模條件與適用范圍，導(dǎo)致了灰色模型之間的兼容性差，本文通過在灰色模型中引入因變量滯后值、線性修正項及常數(shù)修正項，構(gòu)建了一種強兼容性的灰色通用預(yù)測模型(CGPM)，該模型可以通過參數(shù)變化實現(xiàn)與現(xiàn)有主流灰色預(yù)測模型的等價轉(zhuǎn)換，能實現(xiàn)對單變量序列與多變量序列及齊次與非齊次指數(shù)序列的有效模擬。研究成果解決了傳統(tǒng)主流灰色預(yù)測模型之間兼容性差的問題，對提高灰色模型通用性與普適性，促進灰色預(yù)測模型與實際管理問題的有效對接，具有積極意義。如何實現(xiàn)對CGPM模型的初始值、背景值、分?jǐn)?shù)階及病態(tài)性等問題的的系統(tǒng)研究，是本研究團隊下一步的主要工作內(nèi)容。

表4 CGPM模型與GM(0,6)模型的模擬值與模擬誤差

[1] Deng Julong. Control problem of grey systems [J]. System Control Letter, 1982, 1(5): 288-294.

[2] Liu Sifeng, Lin Y. Grey system theory and applications [M]. Berlin Heidelberg: Springer-Verlag, 2010.

[3] Xia Min, Wong W K. A seasonal discrete grey forecasting model for fashion retailing [J].Knowledge-based Systems, 2014, 57: 119-126.

[4] 姚天祥, 劉思峰, 黨耀國. 初始值優(yōu)化的離散灰色預(yù)測模型[J]. 系統(tǒng)工程與電子技術(shù), 2009, 31(10): 2394-2398.

[5] 戴文戰(zhàn). 基于函數(shù)cot(xα)變換及背景值優(yōu)化的灰色建模[J]. 浙江大學(xué)學(xué)報(工學(xué)版), 2010, 44(7): 1368-1372.

[6]WeiYong,ZhangYi.Acriterionofcomparingthefunctiontransformationstoraisethesmoothdegreeofgreymodelingdata[J].TheJournalofGreySystem.2007, 19 (1):91-98.

[7] 熊萍萍, 黨耀國, 姚天祥,等. 灰色Verhulst模型背景值優(yōu)化的建模方法研究[J]. 中國管理科學(xué), 2012, 20(6):155-159.

[8]WeiYong,ZhangYi.Anessentialcharacteristicofthediscretefunctiontransformationtoincreasethesmoothdegreeofdata[J].TheJournalofGreySystem, 2007, 19(3): 293-300.

[9]ZengBo,ChenGuo,LiuSifeng.Anovelintervalgreypredictionmodelconsideringuncertaininformation[J].JournaloftheFranklinInstitute, 2013,350(10): 3400-3416.

[10]XieNainming,LiuSifeng.Intervalgreynumbersequencepredictionbyusingnon-homogenousexponentialdiscretegreyforecastingmodel[J].JournalofSystemsEngineeringandElectronics, 2015, 26(1): 96-102.

[11] 曾波,劉思峰,孟偉. 具有主觀取值傾向的離散灰數(shù)預(yù)測模型及其應(yīng)用[J]. 控制與決策, 2012, 27(9): 1359-1364.

[12]XieNaiming,LiuSifeng.Discretegreyforecastingmodelanditsoptimization[J].AppliedMathematicalModeling, 2009,33(2):1173-1186.

[13] 曾波, 孟偉, 劉思峰,等. 面向災(zāi)害應(yīng)急物資需求的灰色異構(gòu)數(shù)據(jù)預(yù)測建模方法[J]. 中國管理科學(xué), 2015, 23(8): 85-91.

[14] 孟慶良, 何林, 朱慧明,等. 基于GM(1,1)模型的Kano質(zhì)量要素分類動態(tài)預(yù)測方法[J]. 中國管理科學(xué), 2015, 23(9):140-145.

[15]LiuJun,XiaoXinping.TherelationshipofdiscretegreyforecastingmodelDGMandGM(1,1)model[J].JournalofGreySystem, 2014, 26(4): 14-31.

[16]XieNaiming,ZhuChaoyu,ZhengJing.Expansionmodelingofdiscretegreymodelbasedonmulti-factorinformationaggregation[J].JournalofSystemsEngineeringandElectronics, 2014, 25(5): 833-839.

[17]XiaoXinping,GuoHuan,MaoShuhua.Themodelingmechanism,extensionandoptimizationofgreyGM(1,1)model[J].AppliedMathematicalModeling, 2014, 38(5-6): 1896-1910.

[18]ChenCI,HuangSJ.ThenecessaryandsufficientconditionforGM(1,1)greypredictionmodel[J].AppliedMathematicsandComputation, 2013, 219(11): 6152-6162.

[19]ZengBo,LiChuan,ChenGuo,etal.Equivalencyandunbiasednessofgreypredictionmodels[J].JournalofSystemsEngineeringandElectronics, 2015, 26(1): 110-118.

[20] 肖新平, 毛樹華. 灰預(yù)測與決策方法[M]. 北京：科學(xué)出版社, 2013.

[21] 郭曉君, 劉思峰, 楊英杰. 基于自憶性原理的多變量MGM(1,m)耦合系統(tǒng)模型構(gòu)建及應(yīng)用[J]. 中國管理科學(xué), 2015, 23(11):113-118.

[22] 于志軍, 楊善林,章政,等. 基于誤差矯正的灰色神經(jīng)網(wǎng)絡(luò)股票收益率預(yù)測[J].中國管理科學(xué),2015, 23(12):21-26.

ResearchingonAGreyCommonPredictionModelingwithStrongCompatibilityandItsProperties

ZENGBo1,LIUSi-feng2,QUXue-xin3

(1.College of business planning, Chongqing Technology and Business University, Chongqing 400067, China;2.College of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;3.National Research Base of Intelligent Manufacturing Service,Chongqing Technology and Business University, Chongqing 400067, China)

The complicacy of predictive modeling object gives rise to the diversity of form and mutual non-compatibility of structure of grey models. A grey common prediction modeling with powerful compatibility (CGPM) is established through putting the lagged item of dependent variable, corrective terms of linear and constant into grey model. The transformation conditions and equivalence properties between CGPM model and multivariable grey models which include GM(1, N) and GM(0, N) and single variable grey models including GM(1, 1), DGM(1, 1) and NDGM(1, 1) are proved in this paper. The effectiveness of CGPM model is verified by some calculation examples. The study findings have some positive significance for optimizing the structure of grey model and improving the commonality and universality of grey model.

grey theory; prediction model; powerful compatibility; model transformation

1003-207(2017)05-0150-07

10.16381/j.cnki.issn1003-207x.2017.05.018

2016-01-25；

2016-05-24

國家自然科學(xué)基金資助項目(71271226)；重慶市社科規(guī)劃委托項目(2016WT37)；重慶市教育科學(xué)規(guī)劃課題(2012-GX-142)；中國科協(xié)重大招標(biāo)項目(2016ZCYJ06)

曾波(1975-)，男(漢族)，四川威遠(yuǎn)人，重慶工商大學(xué)商務(wù)策劃學(xué)院教授，工學(xué)博士，研究方向：預(yù)測建模方法的研究，E-mail:zbljh2@163.com.

N941.5

A