一種多非完整移動機器人分布式編隊控制方法

李苗，劉忠信，陳增強

(1.南開大學津南校區 計算機與控制工程學院，天津 300353； 2.天津市智能機器人技術重點實驗室，天津 300353)

一種多非完整移動機器人分布式編隊控制方法

李苗，劉忠信，陳增強

(1.南開大學津南校區 計算機與控制工程學院，天津 300353； 2.天津市智能機器人技術重點實驗室，天津 300353)

本文研究了多非完整移動機器人編隊控制算法。在該算法中，參考軌跡被視為虛擬領導者，只有部分機器人可以接收到領導者信息，機器人之間只能進行局部信息交互。利用坐標變換將機器人系統的編隊問題轉化為變換后系統的一致性問題，在持續激勵的條件下，設計了一種分布式控制算法，通過圖論與Lyapunov 理論證明了該分布式控制算法可以使移動機器人隊伍指數收斂于期望隊形，并使隊形的幾何中心指數收斂到參考軌跡。最后，數值仿真驗證了該控制算法的有效性。

非完整移動機器人；編隊控制；一致性；分布式控制

近年來，隨著移動機器人技術的發展，多機器人的協調控制受到了越來越多的關注。多移動機器人通過協作能完成單個機器人不能完成的任務，因此在地理勘測、巡邏偵察、安全救援和運輸大型貨物等領域具有廣闊的應用前景。編隊控制是一個典型的多機器人協調問題，是研究其他協調問題的基礎，其控制算法主要包括基于行為法[1]、領航-跟隨法[2-3]、虛擬結構法[4-8]和人工勢場法[5]等。

移動機器人存在非完整約束和非線性特性，因此對機器人的控制更有難度。文獻[6]研究了非完整移動機器人系統的一致性問題，提出了一個線性時不變連續狀態反饋，使系統狀態變量達到了一致。文獻[7]通過坐標變換將機器人的運動模型變換成鏈式結構，利用反步法設計的軌跡跟蹤控制器達到了期望的效果。文獻[8]采用一致性算法與虛擬結構法研究了自主水下航行器小尺度編隊控制問題，設計的跟蹤控制律使AUV在有限時間內實現了對參考軌跡的跟蹤。文獻[9]將虛擬結構法和反步法相結合，提出的非線性控制算法解決了機器人編隊問題，但該算法要求機器人速度不能為0。

隨著多智能體協同控制理論的發展，它的控制策略已經被應用在多非完整移動機器人編隊控制中。文獻[10]研究了離散模型的多智能體領航跟隨編隊控制算法，在該算法中，通過引入基于鄰居的局部控制律以及基于鄰居的狀態估計規則設計了一種新型控制器，經過理論分析，給出了固定拓撲和切換拓撲時系統穩定編隊的充分條件。文獻[11]在每個移動機器人都知道參考軌跡信息的條件下，提出了一個移動機器人編隊控制器。在持續激勵的條件下，文獻[12-13]利用非自治系統的級聯控制方法和線性智能體的協同控制方法，將非完整約束多個體系統的控制問題轉化為多個線性時變系統的控制問題，文中的控制律可以實現系統K-指數穩定的跟蹤控制。文獻[14]提出了一種新坐標變換，將移動機器人編隊問題轉化為狀態變量實現一致的問題，設計的分布式控制律可以使系統指數收斂于期望軌跡，但是每個機器人個體都要知道參考軌跡的角速度。

在上述工作的基礎上，本文進一步研究了非完整移動機器人編隊控制問題。文中通過引入坐標變換公式，將機器人編隊問題轉化為一致性問題。在持續激勵條件下，利用鄰居信息設計了分布式控制協議，然后用圖論和Lyapunov方法，在理論上證明了該控制協議的正確性。最后，文中通過MATLAB仿真來驗證該控制算法的可行性。不同于文獻[12,14]，本文把參考軌跡視為虛擬領導者，它的狀態信息只有部分跟隨者能接收到。與文獻[11]相比，考慮機器人之間只能進行局部信息交互，利用圖論和Lyapunov方法設計的分布式控制律，可以保證整個機器人隊伍指數收斂于指定隊形，并且隊形幾何中心收斂到參考軌跡。

1 問題的提出

考慮n個非完整約束移動機器人組成的系統，系統中的每個機器人具有相同的結構，有兩個驅動輪和一個自由輪，如圖1所示。用θ={1,2,…,n}表示移動機器人序列，移動機器人i的運動學表達式為

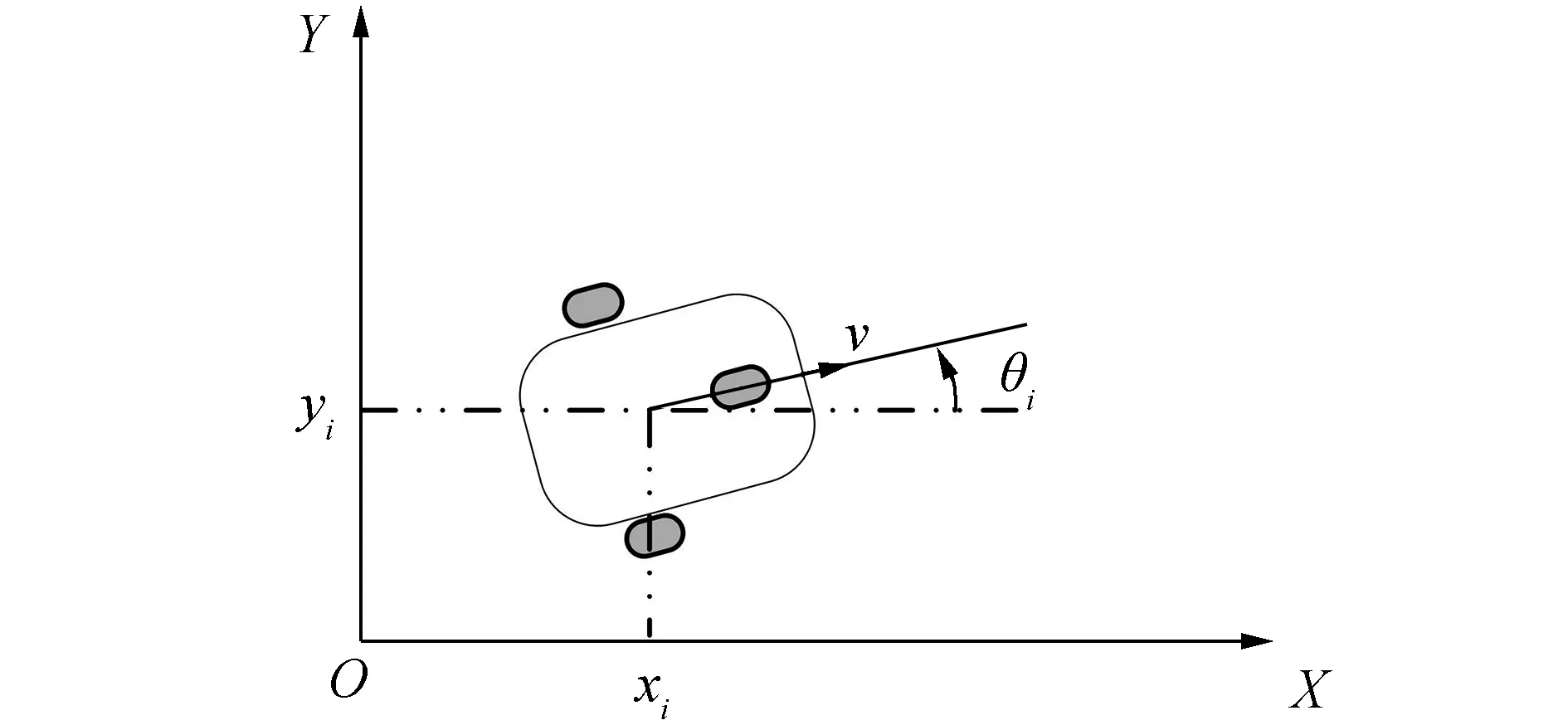
圖1 移動機器人示意圖Fig.1 The sketch of mobile robot

圖論可以清晰完整地模擬移動機器人之間的連接關系，本文利用無向圖來描述多移動機器人之間的通信關系。令G=(V,E)表示一個無向圖，V={v1,v2,…,vn}表示由n個節點構成的節點集，E?V×V表示邊的集合。如果(vi,vj)∈E，則表示機器人i與機器人j可以接收到彼此的信息。

無向圖G的鄰接矩陣為A=[aij]∈Rn×n，其中aij表示(vi,vj)連接權重，即

在無向圖中，(vi,vj)∈E，則(vj,vi)∈E，且aij=aji，?i≠j。如果(vi,vj)∈E，那么vj是vi的鄰居頂點。我們定義頂點vi的鄰居點集合為Ni={j∈V:(vi,vj)∈E,?i≠j}。

無向圖G的度矩陣為D=diag(d1,d2,…,dn)，那么圖G的拉普拉斯(Laplacian)矩陣為L=D-A。

假設n個移動機器人形成編隊隊形F，(p0x,p0y)為編隊隊形F的幾何中心，(pix,piy)表示機器人i相對于隊形F幾何中心的期望位置矢量，即

為了計算簡單，不失一般性，我們假設p0x=0，p0y=0。

整個機器人隊伍的參考軌跡T的運動學模型為

式中:v0、ω0為已知時變函數。在實際應用中，機器人群體完成特定任務時，只有一個或者幾個移動機器人知道任務的信息，其他機器人個體需要通過與鄰居的信息交互，才能完成特定的任務。因此為了符合實際，本文將參考軌跡T視為虛擬領導者0的運動軌跡，假設參考軌跡的信息并不是全局已知的，采用牽制控制的思想，來實現多機器人編隊控制。移動機器人i與虛擬領導者0之間的通信關系用對角矩陣B=diag(b1,b2,…,bn)來表示。如果機器人i能獲得虛擬領導者0的信息，則對角元素bi=1，否則bi=0。

分布式編隊控制的目標是基于鄰居和自己的 狀態信息，為每個機器人設計控制器，使整個機器人隊伍形成編隊隊形F，同時幾何中心實現對虛擬領導者0的軌跡跟蹤，即設計的控制器滿足式(4)～(7)：

在介紹分布式控制算法之前，先給出本文的一些符號表示和多機器人系統滿足的兩個假設，以及后面證明所需要用到的兩個重要引理。

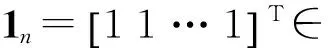
假設1[12-13]ω0是持續激勵信號，即存在正常數α1、α2和δ，使得對于所有的t>0，滿足

假設2 圖G是無向連通的，至少存在一個移動機器人和虛擬領導者0是直接連通的，且這種連通是單向的。

引理1[15]如果實數矩陣A∈Rn×n正定對稱，那么對于任意向量x∈Rn都滿足下面條件

λmin(A)xTx≤xTAx≤λmax(A)xTx

引理2[16]對于矩陣B=diag(b1,b2,…,bn)>0，如果無向圖G連通，那么矩陣L+B是正定的。

2 分布式控制算法

2.1 控制器的設計

為了便于控制器的設計，我們將移動機器人的運動學模型進行坐標變換，使用如下的坐標變換[13]：

同時，控制輸入的變換方程為

通過上述變換，機器人i運動學模型變為

式中：0≤i≤n；k0>0；x1i,x2i,x3i表示系統坐標變換后的狀態量；u1i,u2i表示系統坐標變換后控制輸入。

通過上面的坐標變換式(8)，多移動機器人編隊問題轉化為新狀態變量x1i,x2i,x3i實現一致的問題。采用誤差控制策略，定義變換后的狀態誤差為

對式(11)求導可得

為了解決多機器人編隊問題，把狀態誤差系統式(12)～(14)分解為一個一階子系統和一個二階子系統，其中一階子系統的運動學方程為式(12)，二階子系統的運動學方程為式(13)和式(14)。考慮只有部分機器人與虛擬領導者0有信息交互，設計u1i，使得一階子系統式(12)在有限時間內收斂于0；設計u2i，使得二階子系統式(13)和式(14)指數收斂于0。構造如下的分布式控制律：

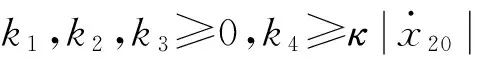
根據控制律式(15)和式(16)，以機器人1為例，控制算法的原理框圖如圖2所示。它由兩部分組成，一部分為機器人坐標變換i∈θ，另一部分為分布式控制器。

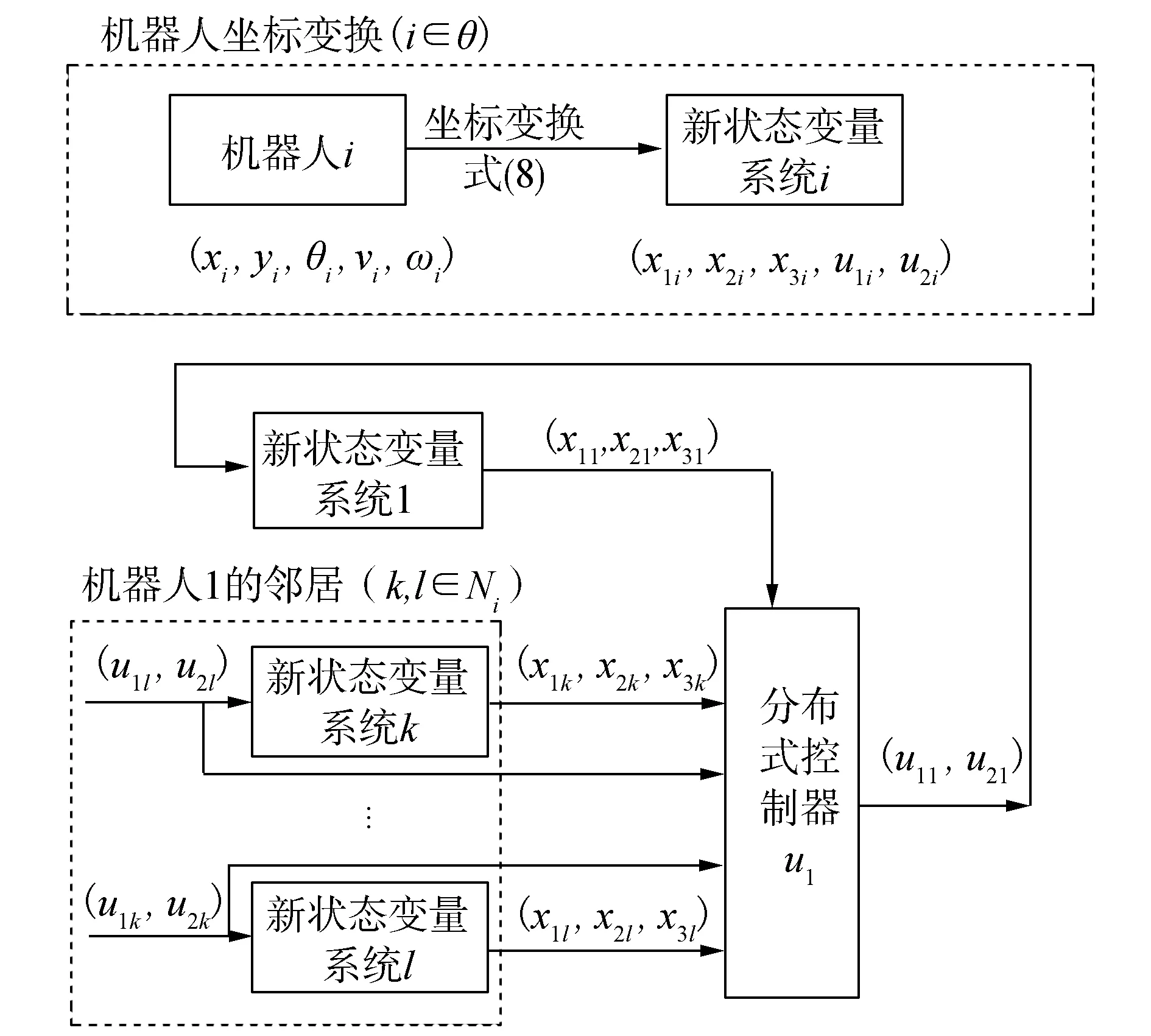
圖2 移動機器人1控制原理框圖Fig.2 The control principle block diagram of mobile robot 1

2.2 穩定性分析

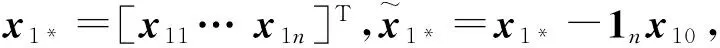
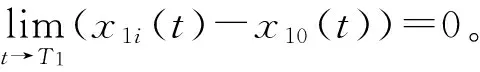
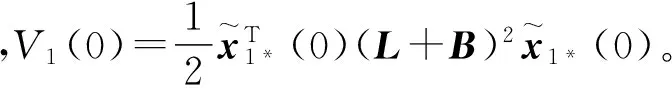
證明 針對系統式(18)，構造如下的Lyapunov函數：

根據引理1，可得到

對V1求導可得

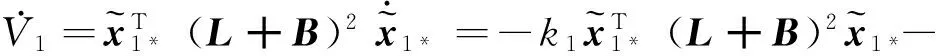
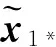
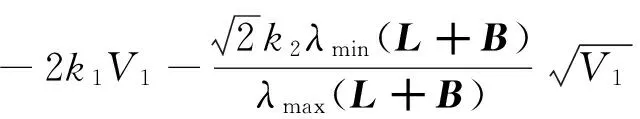
求解上述微分不等式可得：當0≤t≤T1時，

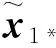
收斂時間T1依賴于初始值V1(0)，滿足下式：

定理1證畢。

從定理1中u1i的收斂時間T1表達式可以看出，k2影響一階子系統的收斂速度，k2越大，收斂速度越快。但是k2越大，由于sign(·)函數不連續所造成的抖振現象對系統穩定性影響越大，所以，選擇k2時，需要綜合考慮控制精度、收斂速度等方面影響。二階子系統表達式(13)和式(14)中存在變量u1i，所以一階子系統的動態特性會影響二階子系統的動態特性，但是一階子系統式(12)穩定性并不受二階子系統中變量的影響。由定理1可知，在控制律式(15)的作用下，x1i,u1i在有限時間T1內收斂于x10,u10。所以下面我們只考慮二階子系統式(13)和式(14)。

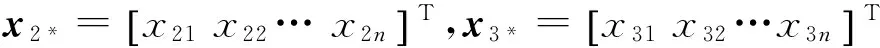
u1*=diag(u11,u12,…,u1n)

基于分布式控制協議式(16)，二階子系統式(13)和式(14)閉環特性可以表示為下面的矩陣形式：

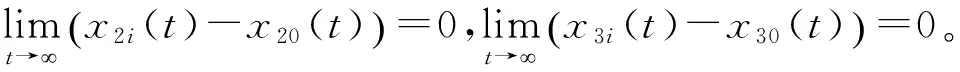
證明 由定理1可知，當t>T1時，u1i(1≤i≤n)收斂到u10，下面分兩步來證明定理2。

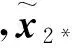
對閉環系統式(19)構造的Lyapunov函數為

根據引理1可以得到

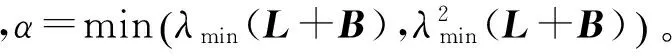
對V2沿著軌跡式(19)求導可得

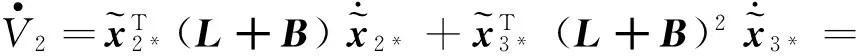
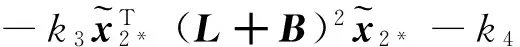
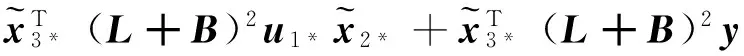
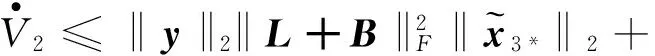
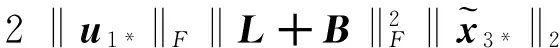
求解上述微分不等式可得

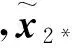
根據定理1，當t>T1時，u1i=u10，x1i=x10，則二階子系統閉環表達式(19)化簡為

則式(22)整理為

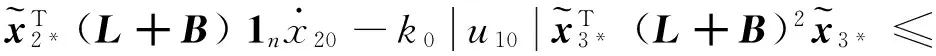
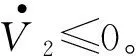
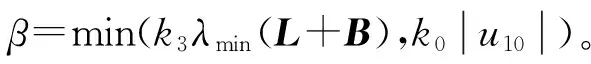
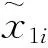
3 仿真結果分析

本節中，我們用MATLAB對移動機器人系統進行了仿真研究，仿真中n=4，移動機器人之間的通信拓撲為

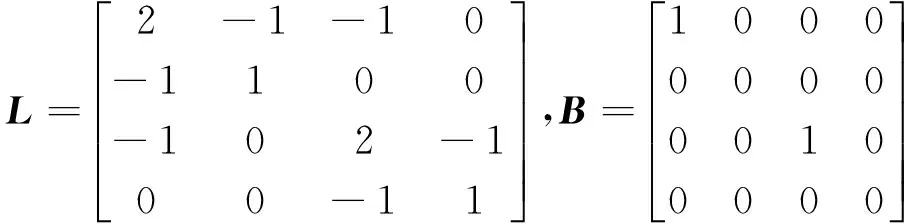
期望的編隊隊形F為一個正方形：

(p1x,p1y)=(1,1)，(p2x,p2y)=(-1,1)

(p3x,p3y)=(-1,-1)，(p4x,p4y)=(1,-1)

在圖3中，每個四邊形中的4個*表示4個跟隨者，實線和虛線分別表示虛擬機器人0和編隊幾何中心的運動軌跡，從圖中可以看出4個跟隨者形成了指定正方形編隊，同時編隊隊形的幾何中心收斂到虛擬領導者0的運動軌跡。圖4和圖5分別給出了3個跟隨者的控制輸入ωi,vi(i=1,2,3,4)，從圖中可以看出，在15 s之后，ωi,vi收斂到ω0,v0。圖6～8分別表示4個跟隨者與虛擬機器人0的航角和位置之間的誤差。在20 s后，4個跟隨者與虛擬領導者0之間的航角誤差為0，x軸和y軸方向的位置誤差分別為pix和piy(i=1,2,3,4)。從上述仿真實驗可以看出，所設計的控制器可以使移動機器人形成期望的編隊。

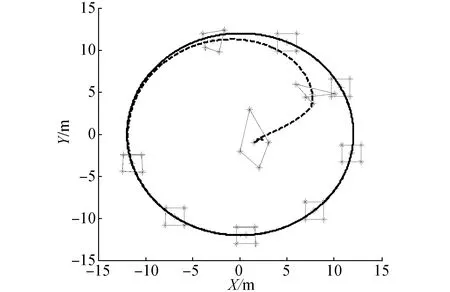
圖3 移動機器人編隊運動軌跡Fig.3 Trajectory of tracking of mobile robots formation

圖4 移動機器人控制輸入 ωFig.4 The control input ω of the mobile robots

圖5 移動機器人控制輸入vFig.5 The control input v of the mobile robots

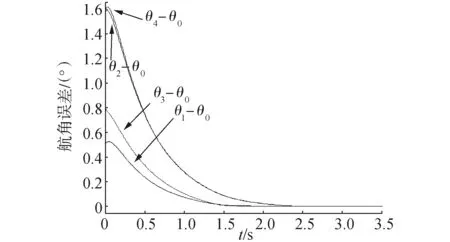
圖6 航角誤差θeFig.6 Heading errors θe

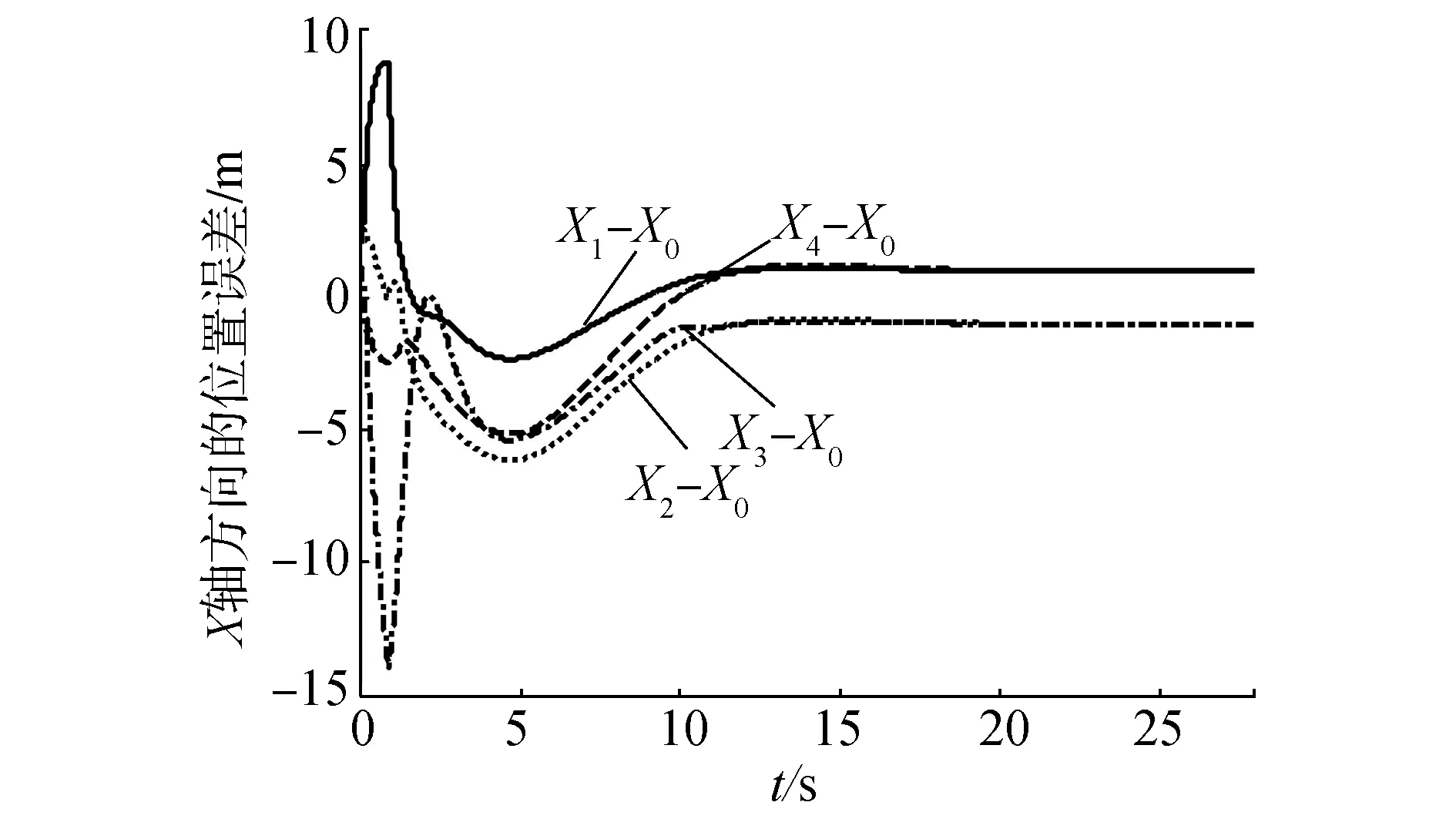
圖7 X軸方向的位置誤差xeFig.7 Position errors in X coordinates

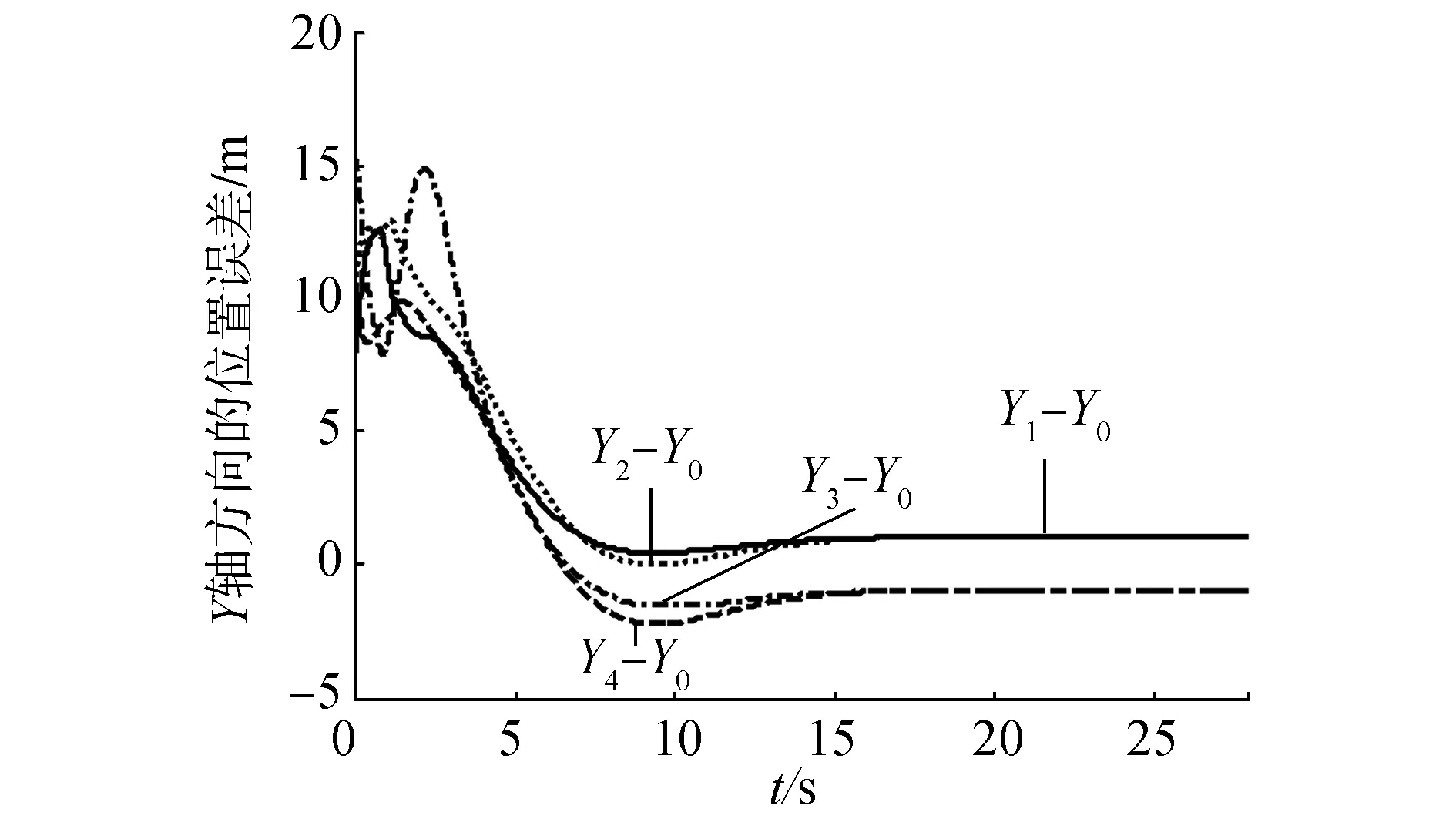
圖8 Y軸方向的位置誤差yeFig.8 Position errors in Y coordinates

4 結束語

本文以多非完整移動機器人為研究對象，通過坐標變換將編隊問題轉化為移動機器人狀態量的一致性問題。在持續激勵信號作用下，利用鄰居狀態信息設計了分布式控制協議，然后用圖論和Lyapunov方法，在理論上證明了該控制協議可以很好地解決機器人編隊問題。最后，通過MATLAB對該控制算法進行了驗證。從仿真實驗結果可以看出，本文提出的控制算法可靠性好，能在較短時間內順利形成編隊。本文假設通信拓撲結構是無向連通的，但在實際應用中，系統之間的通信網絡往往是有向的或者存在時滯，所以，將來的研究工作將圍繞著有向通信拓撲來開展。

[1]BALCH T, ARKIN R C. Behavior-based formation control for multirobot teams[J]. IEEE transactions on robotics and automation, 1998, 14(6): 926-939.

[2]SHAO J, XIE G M, WANG L. Leader-following formation control of multiple mobile vehicles[J]. IET control theory & applications, 2007, 1(2): 545-552.

[3]DESAI J P, OSTROWSKI J P, KUMAR V. Modeling and control of formations of nonholonomic mobile robots[J]. IEEE transactions on robotics and automation, 2001, 17(6): 905-908.

[4]TAN K H, LEWIS M A. Virtual structures for high-precision cooperative mobile robotic control[C]//Proceedings of the 1996 IEEE/RSJ International Conference Intelligent Robots and Systems’96. Osaka, Japan, 1996: 132-139.

[5]KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[J]. International journal of robotics research, 1986, 5(1): 90-98.

[6]ZHAI G, TAKEDA J, IMAE J, et al. Towards consensus in networked non-holonomic systems[J]. IET control theory & applications, 2010, 4(10): 2212-2218.

[7]YUAN Z P, WANG Z P, CHEN Q J. Trajectory tracking control of a nonholonomic mobile robot[C]//Proceedings of the 8th IEEE International Conference on Control and Automation. Xiamen, China, 2010: 2207-2211.

[8]袁健, 唐功友. 采用一致性算法與虛擬結構的多自主水下航行器編隊控制[J]. 智能系統學報, 2011, 6(3): 248-253. YUAN Jian, TANG Gongyou. Formation control of autonomous underwater vehicles with consensus algorithms and virtual structure[J]. CAAI transactions on intelligent systems, 2011, 6(3): 248-253.

[9]CHEN Lei, MA Baoli. A nonlinear formation control of wheeled mobile robots with virtual structure approach[C]//Proceedings of the 34th Chinese Control Conference. Hangzhou, China, 2015: 1080-1085.

[10]王中林, 劉忠信, 陳增強, 等. 一種多智能體領航跟隨編隊新型控制器的設計[J]. 智能系統學報, 2014, 9(3): 298-306. WANG Zhonglin, LIU Zhongxin, CHEN Zengqiang, et al. A kind of new type controller for multi-agent leader-follower formation[J]. CAAI transactions on intelligent systems, 2014, 9(3): 298-306.

[11]DONG Wenjie, FARRELL J A. Decentralized cooperative control of multiple nonholonomic dynamic systems with uncertainty[J]. Automatica, 2009, 45(3): 706-710.

[12]CAO Kecai, YANG Hao, JIANG Bin. Formation tracking control of nonholonomic chained form systems[C]//Proceedings of the 10th IEEE International Conference on Control and Automation (ICCA). Hangzhou, China, 2013: 846-851.

[13]CAO Kecai, JIANG Bin, CHEN Yangquan. Cooperative control design for non-holonomic chained-form systems[J]. International journal of systems science, 2015, 46(9): 1525-1539.

[14]PENG Zhaoxia, WEN Guoguang, Rahmani A, et al. Distributed consensus-based formation control for multiple nonholonomic mobile robots with a specified reference trajectory[J]. International journal of systems science, 2015, 46(8): 1447-1457.

[15]方勇純, 盧桂章. 非線性系統理論[M]. 北京: 清華大學出版社, 2009: 1-151.

[16]HONG Yiguang, HU Jiangping, GAO Linxin. Tracking control for multi-agent consensus with an active leader and variable topology[J]. Automatica, 2006, 42(7): 1177-1182.

A distributed formation control method for multiple nonholonomic mobile robots

LI Miao1,2, LIU Zhongxin1,2, CHEN Zengqiang1,2

(1. College of Computer and Control Engineer, Jinnan Campus, Nankai University, Tianjin 300353, China; 2. Tianjin Key Laboratory of Intelligent Robotics, Tianjin 300353, China)

This paper addresses the algorithm of formation control for multiple nonholonomic mobile robots. The reference trajectory was represented by a virtual leader whose states were available to a subset of the following mobile robots and the robots only interacted with each other locally. Coordinate transformation was proposed to convert the formation control problem for multiple nonholonomic mobile robots into a state consensus problem. Under the restriction of persistent excitation on reference trajectories, distributed control laws were proposed for achieving the formation control objectives. Using the Lyapunov function and graph theory, rigorous proofs show that the group of mobile robots can exponentially converge to a desired geometric formation pattern and its centroid can move along the reference trajectory. The validity of the proposed control method is verified by numerical simulation.

nonholonomic mobile robots; formation control; consensus; distributed control

李苗，女，1991 年生，碩士研究生，主要研究方向為多智能體系統控制、人工智能系統與控制。

劉忠信，男，1975 年生，教授，博士生導師，中國人工智能學會智能空天系統專業委員會委員、中國智能物聯系統建模與仿真專業委員會委員，主要研究方向為多智能體系統、復雜動態網絡、計算機控制與管理。

陳增強，男，1964 年生，教授，博士生導師，主要研究方向為智能預測控制、混沌系統與復雜動態網絡、多智能體系統控制。

10.11992/tis.201512021

http://kns.cnki.net/kcms/detail/23.1538.TP.20170227.2155.018.html

2015-12-12.

日期：2017-02-27.

國家自然科學基金項目(61573200, 61273138)；天津市自然科學基金項目(13JCYBJC17400, 14JCYBJC18700,14JCZDJC39300).

劉忠信. E-mail:lzhx@nankai.edu.cn

TP18

A

1673-4785(2017)01-0088-07

李苗，劉忠信，陳增強.一種多非完整移動機器人分布式編隊控制方法[J]. 智能系統學報， 2017, 12(1): 88-94.

英文引用格式：LI Miao, LIU Zhongxin, CHEN Zengqiang. A distributed formation control method for multiple nonholonomic mobile robots[J]. CAAI transactions on intelligent systems, 2017, 12(1): 88-94.