由一道關于三角函數范圍題目引發的思考
廣東省廣州市華南師范大學 陳銘睿
由一道關于三角函數范圍題目引發的思考
廣東省廣州市華南師范大學 陳銘睿
求范圍問題的應用一直是一個熱門考點,且其中包含的知識很廣泛,比較考驗學生的綜合應用能力。其中三角函數范圍是一個較難突破的點,角的范圍和三角函數的取值相互制約。而學生在三角函數取值中經常會出現漏解和錯解的情況,其原因很有可能是忽略了題中一些條件,將角的范圍擴大化。本文就一道綜合性較強的求解三角函數范圍的題目,探討一下其中可以深究的問題。
一、案例呈現
我們來看題目:如圖是一個三角形,其中A,B,C三個角分別對應的邊長為a,b,c,且過A作BC邊上的高AD,AD長度為a,試求的范圍。
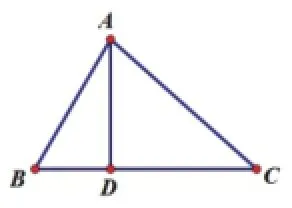
解析:首先觀察我們所要求的式子,發現為兩式之和且互為倒數的形式,又由于b,c都為正實數,能較容易想到使用如均值不等式的形式,在本題中就是時能取等號。
二、完善探究
直到這里原式的范圍就出來了,一些習題冊或試卷中所給的參考答案到這里就結束了,大同小異如此一般。 但是在這里我們不妨來思考一個問題:題中的上限值是否能取到,即A的取值是否能讓成立?
平時遇到類似的問題時,許多人可能做到這一步的時候,理所當然地認為正弦函數能取到1。但由于所用到的角度是在一個三角形中的,是有限制的,所以這里應該還要檢驗取到的值是否符合題目限制條件的要求,下面我們來探究一下角的取值范圍。
由于這里的三角形沒有特殊說明,故我們需要分情況討論。第一種是AD在三角形內,落在BC上,第二種AD是在三角形外,落在BC的延長線上。
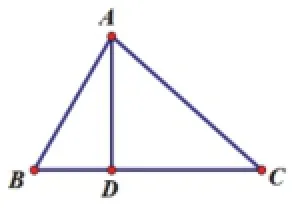
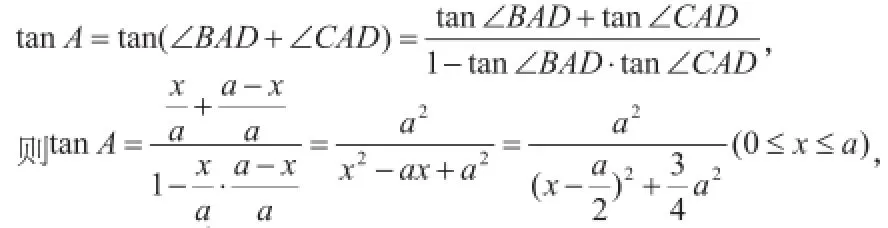
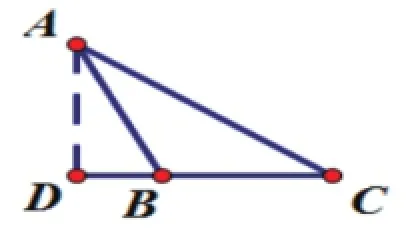
再來看第二種情況,如圖,假設BD長度為x,則DC=a+x,且利用正切函數的差公式有:
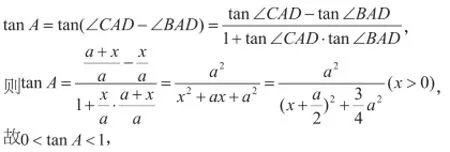
三、反思小結
眾所周知,嚴謹性是數學科學的一個基本特點。所謂數學的嚴謹性,就是指對數學結論的敘述必須精確,結論的論證過程必須嚴格、周密。以這道題為例,許多同學可能只注重結果,對上答案了可能就不會再考慮這個答案是否完整,是否嚴密。現在關于數學的輔導和練習資料眾多,其內容的質量也是參差不齊的。對于一些比較依賴答案、比較缺少自己思考的學生來說,參考一些不嚴謹甚至存在錯誤的資料,會非常不利于他們數學的學習。
像這種類型的題目有很多,學生也常常求出最后的范圍后就以為完成了,而不會去檢驗這個范圍是否合理。教師在進行教學時,首先自身應該做到思維縝密、言必有據,在平時的教學時要注意培養學生思維過程和解題過程的嚴謹性、完整性。 最后,引用數學上一句經典的話:培養學生嚴謹的治學態度不一定是他們學好數學的充要條件,但肯定是一個必要條件。
book=76,ebook=78
陳銘睿,(1996-07-),男,漢族,廣東省珠海市人,華南師范大學學生,本科,研究方向:數學與應用數學)

