高中數學教學中應用向量教學強化學生的建模思路
江蘇省金湖中學 林 煒
高中數學教學中應用向量教學強化學生的建模思路
江蘇省金湖中學 林 煒
高中數學教學中,特別是向量教學中,可以讓學生學會應用向量模型解決各類數學問題,強化學生的建模思路。
高中數學;向量;建模
建模是指找到一個解決問題的模型,能夠批量解決數學問題的方法。高中數學教師要在教學中強化學生的建模能力。向量,是一種與各種數學知識都有直接聯系的知識,學生可以應用向量模型解決各類數學問題,教師可以在向量教學中強化學生的建模思路。
一、應用向量學習建立整體建模思路
部分學生不理解要如何在解決數學問題的過程中建模,數學教師可以引導學生具備整體建模思路,讓學生理解建模思路的意義。向量是一個能夠呈現數學問題的幾何問題與數量問題的方法,學生應用向量的建模方法,可以讓數學問題變得簡潔。教師可以引導學生從向量問題著手,嘗試培養整體建模的能力。
比如以一名數學教師引導學生理解應用向量來建立數學模型為例:現在有一家超市銷售A、B兩種商品,A商品可銷售的總量為x,B商品可銷售的總量為y。A商品的單價是m元/kg,B商品的單價是n元/kg。那么現在有一個人既要購買A,又要購買B,學生能不能應用向量的方式來表示他購物的情況呢?學生經過思考,認為可以應用坐標圖來表示他購物的情況。其中表示他購買商品的數量、表示他購買商品的價格,即為他商品購買的情況。學生在立何幾何圖形上,可以應用向量來探討他購買商品的情況。如果有必要,學生也可以應用代數的方式來詮釋這一模型,即那么他購買商品的情況為學生只要建立了一個探討某一事物變化規律的模型,就能應用這套模型解決與這件事情有關的問題。數學教師可以引導學生理解,商品購買的情況如果為一個數學問題,學生要找到影響這個問題的因素,并把這個因素用數學關系描述出來,就是數學模型,學生只要建立了這個數學模型,就能用這一數學公式來解釋一切與此數學問題有關的因素問題。
二、應用向量學習建立性質建模思路
部分學生在學習建模知識的時候,即使理解了建模思路是解決數學問題的思路之一,也不知道要如何才能建立數學模型,數學教師可以應用向量的建模教學著手,引導學生學會抓住數學問題的性質,讓學生學會建立數學問題的模型。
以數學教師引導學生思考以下數學問題為例:已知非零向量a, b,如果相互垂直,那么等于多少?教師可以引導學生思考:有距離相同但是性質相反的特質,即這兩個數學問題具有“a”、“2b”兩個相同的數量,然而方向一個是“+”,一個是“-”。現在,這兩個數學問題還相互垂直。如果把這個數學問題繪成向量圖形,會是什么呢?學生們可以看到,可以將這個數學問題繪制成一個菱形問題,繪制的圖形如圖1。現學生可以以菱形圖形為模型,解決這個問題,這個數學問題的數學模型為菱形的邊長性質,由該性質可得結合已知條件可得這道習題的關鍵,就是學生要找到數學問題的特征,學生在解決這個數學問題的時候,如果應用數形結合的方法,就能分析出它的數學特征就是一個菱形問題的計算,即學生的數學模型就是菱形邊長的求值問題,學生只要找到影響菱形邊長的因素,計算出菱形的邊長,就能快速獲得數學問題的答案。
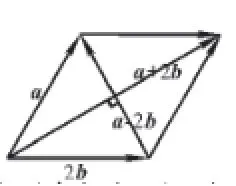
圖1
當學生理解了建立數學模型的整體思路就是找到需要解決的數學問題及影響數學問題的因素以后,還需要了解要如何才能找到與之有關的因素呢?數學教師可以引導學生從抓數學問題的特征著手分析。學生只要學會找到數學問題的特殊特征,了解影響數學問題特殊牲的因素,便能找到解決數學問題的途徑。
三、應用向量學習創新建模材料思路
部分學生在解決數學問題的時候,表示有些數學問題的性質不明顯,難以應用數學性質來建立數學模型,那又該如何解決數學問題呢?數學教師可引導學生結合解題的需要來整合數學材料,完成數學模型建立的方法解決數學問題。向量數學問題的轉換性特別強,教師可以應用向量教學引導學生建立創新建模材料思路。以下面的習題為例:
教師可以引導學生看到兩個數學問題。第一,這一數學問題似乎是可以應用向量公式作為模型來解決的。第二,如果通過整合,可以嘗試把這一數學問題變為具有向量特征的數學問題。學生直接分析時,看不到它數學問題的特征。然而學生經過仔細分析,發現只要巧妙整合這一公式,還是能把它整合成向量公式的,只要把它整合成向量公式,就能把向量公式作為模型解決數學問題。
教師要引導學生理解,學生在具有了抓住數學問題的特征思路以后,還要以數學特征為核心,整合數學公式,為應用數學模型計算做好準備。這是學生建立數學模型能否被創建的關鍵。
向量具有幾何與數量雙重的特征,它適合應用在各種數學問題中。數學教師可通過向量教學引導學生具備這樣的建模思想:第一,引導學生具備抓住解決數學問題核心,分析與數學問題有關因素的建模思想;第二,引導學生具備抓住數學特征,應用數學特征建模的思想;第三,引導學生具備整合數學問題的材料,令適合材料建立模型的思想。只要學生掌握這種建模思路,就能提高解決數學問題的水平。
[1]唐萬敏.淺談高中數學教學中學生創造性思維的激發[J].數學學習與研究(教研版),2009(01).
[2]王劍.高中數學“自主學習”方略組合[J].數學學習與研究,2010(13).
book=75,ebook=77

