初中數學教學中如何培養學生的思維能力
江蘇省濱海縣第一初級中學 陳見昌
初中數學教學中如何培養學生的思維能力
江蘇省濱海縣第一初級中學 陳見昌
數學思維是人們對數學對象的本質、相互關系及其內在規律的概括與間接反映。數學思維作為結果是指數學知識本身,作為過程指的是獲取數學知識和解決數學問題時的思維過程。數學思維有三個特點:其一,連貫性,是指在教學中老師提出某一課題后,學生針對這一課題所進行一系列思考的承前啟后的特征。其二,順序性,是指學生的思維過程必須遵循一定的程序進行。其三,發展性,它體現了學生思維順著課題的難度逐漸增加而積極向前的發展趨勢。在教學中不注意學生這種思維活動的特性,我們的教學過程是無法收到良好的效果的。如不重視學生思維的連貫性,不把學生為某一課題的思維活動當作一個連續過程來看待,就會造成學生思路的紊亂,長久下去,不但會影響學生掌握知識,更重要的是會阻礙學生思維能力的發展。為此,在教學過程中加強學生思維能力的培養,主要有以下幾條途徑:
一、通過概念教學,培養學生的思維能力
在數學概念的教學中,首先要認識到概念引入的必要性,注意創設思維情境,對感性材料進行分析、抽象和概括,講清楚概念的來龍去脈,有利于培養學生創造性的思維能力。其次要進一步對概念定義的結構特征加以分析,明確概念的內涵與外延,在此基礎上再誘導學生歸納其基本性質、應用范圍以及利用性質進行判斷、解題、證題,進而發展學生的思維能力。
二、在數學定理、公式、法則的證明過程中培養學生的思維能力
數學定理、公式、法則的證明過程即是尋求、發現和作出證明的思維過程。數學定理、公式、法則反映了數學對象之間的關系,對于這些關系的認識,要盡量創造條件,從學生已有的知識入手,讓學生了解定理、公式、法則的形成過程,并設法讓學生體會到尋求它們的樂趣。定理、公式、法則的證明方法具有典型性,學生掌握了這些具有代表性的方法后可以舉一反三。通過定理、公式、法則的證明發展學生的創造性思維。當一個定理或公式、法則展現在學生面前時,引導學生從整體上把握它的全貌,憑直覺思維預測其真假,在具有初步確信的基礎上,通過積極的思維活動,從認知結構中提取有關的信息、思路和方法,最后給出嚴謹的邏輯證明。這樣,在證明數學定理、公式、法則的全過程中培養和發展學生的思維能力。
三、在例題教學過程中,培養學生的思維能力
精心選擇講解的例題,在精不在多,要符合典型性、探索性、多解性、拓展性。這就要求對例題進行適當的變換對圖形、條件、結論等進行必要的延伸、拓展。講解例題時,引導學生回憶相關的知識和類似問題,激發學生聯想,留給學生足夠的思考時間,讓學生議、問、答、練。在思維跳躍較大的地方,架設適當的“橋梁”,使學生中斷的思路得以延續。在思維較抽象的地方,要設法幫助他們構成圖形、實例,從中悟出一般性的道理,創設多方位探索情境。當學生面臨多種選擇、多種思路時,幫助學生進行點撥、評價、判斷,引導學生篩選出合理的方案,由此引出新的問題和進一步的思考,同時還要鼓勵學生敢于發表個人的獨特見解。通過例題教學,創設思維情境,引發學生的思維,從而提高學生的思維能力。
四、重視解題教學,培養和發展思維能力
在解題教學過程中,主要從以下幾方面培養和發展思維能力:
(1)精選構思巧妙、概念性強、覆蓋知識面廣、靈活性大的判斷題、選擇題、簡答題進行專項訓練,提高學生的敏捷性和靈活性。
(2)組織學生開展解題思路的討論,剖析各種解題方法的特點。選擇簡捷有創造性的解題思路。拓展學生思維時,要盡可能考慮一題多解、一題多變或多題一解,總結并概括規律,提高學生思維的發散性和變通性。
(3)選擇多層次、思維深刻的綜合題進行審題訓練,要求學生把綜合題分成幾個基本題。分析涉及的基本概念和基本方法,引導學生周密、準確、全面地考慮問題,使他們能發現并找到解題規律,提高學生思維的嚴謹性和綜合性。
(4)在平時練習中有意識地把互逆命題組合在一起交替使用,如多項式的乘法與因式分解、平行線的性質與判定、等腰三角形的性質與判定等在同一題中交替應用,提高學生的辨別能力和逆向思維能力。
(5)多做開放性題。由于開放性題要么條件不全,要么結論不明,因而對思維有更強的鍛煉效果。
五、通過糾錯辨誤教學,培養學生的思維能力
在糾錯辨誤教學過程中,應根據教材和學生的實際,圍繞典型錯誤,做各種有助于學生思考的引導,如:設問、追問、反問、加問或補充必要的舊知識,并隨時根據來自學生反饋的信息來調整引導方式。我認為糾正錯誤的類型和方法主要有以下幾種:
1.糾正因概念混淆引起的錯誤,提高學生思維的批判性
在初中數學中,有些概念如:角平分線與三角形平分線、平方和與和的平方、不大于與小于、解不等式與解方程等,學生容易混淆。例如解不等式x2>1與解方程不易理解“>”與“=”的深刻含義與本質區別,故把x2>1解成x=±1。為此,把方程與不等式解法對比如下:
解法一:兩邊都取算術平方根。
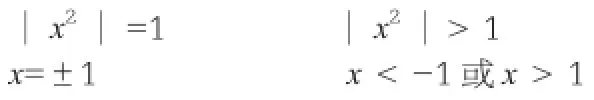
解法二:因式分解法。

通過上述對比分析,學生對于x2>1的正確解答與錯誤解答的本質區別就能深刻理解。此外,常設計一些易錯的問答題、判斷題、選擇題來澄清一些概念性錯誤,從而培養學生辨別正誤的能力,提高其思維的批判性。
2.糾正忽略隱含條件引起的錯誤,提高學生思維的探索性
隱含條件是指題中藏而不露的已知條件,這些條件隱藏在題設背后,不易察覺,易被忽略。
如:二次函數y=ax2+4x+a有最小值了,求a的值。
此解忽略了二次函數有最小值的條件:二次函數系數大于0,而當a=-1時,二次函數有最大值,故應舍去。
在教學過程中可適當安排糾錯的環節,引導學生通過觀察、比較、聯想充分挖掘并利用隱含條件來探尋解題思路,從而提高學生思維的探索性。
3.糾正忽略特例引起的錯誤,提高學生思維的全面性
忽略特例是學生常犯思考不周的毛病,對于特例在教學中的作用不容忽視。
因此,在教學中要經常引導學生注意容易忽視的特例,從而提高學生思維的全面性。
總之,我們應結合數學思維的特點,遵循學生思維的發展規律,在初中數學教學中利用多種渠道培養學生的思維能力,讓學生通過自己的思維來學習數學。
book=79,ebook=81

