“多題一解”例析一類組合數學問題
◎王陸杰
(東北師范大學數學與統計學院,吉林 長春 130024)
“多題一解”例析一類組合數學問題
◎王陸杰
(東北師范大學數學與統計學院,吉林 長春 130024)
多題一解,可以把一道復雜的題和最基本的簡單題建立聯結,從而簡化復雜問題的解決.是轉化與化歸數學思想的重要支柱.本文重點研究從“多題一解”的視角,把看似不同類型組合的問題抽象成一類組合數學問題,并找到一個一般性的程序化解題方法,給出了這一類組合問題的統一公式.
排列組合;分步順序;多題一解
一、引 言
轉化是非常重要的數學思想,多題一解是轉化思想的集中體現.如果能把一道復雜的題和一道簡單的題建立聯結,找到它們有類似的解法,一般可以大大簡化復雜問題的解決.形式上不同的問題往往卻在本質上是一致的,“形不似神似”.
本文借助一道非常基礎的題拋磚引玉,以期能對一類組合數學問題給出程序化的解法,并給出統一的公式,初步揭示了一些表面上有差別的問題其實有著共通的本質的現象.
二、拋磚引玉
有時候玉和磚頭只是外形看上去不同.
(一)拋 磚
一個六位數密碼箱,每一個位置上可以獨立設置0-9十個不同的數字.現有一人隨機輸入一組六位數字,求其能打開箱子的概率.
解:每一個位置互相獨立,每一個位置都有10種選擇.根據分步計數原理:
一共有106種設置方法.
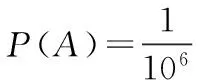
評注:沒有限制條件時,單純的獨立重復試驗問題非常的簡單,如果我們加一點限制條件呢?
(二)換磚再拋
一個六位數密碼箱,每一個位置上可以設置0-9十個不同的數字,但是第一位的數字不能和后面位上的數字相同,問有多少種設置密碼的方法?
分析:和例1非常的像,我們可不可以借助例1的想法來簡化問題呢?新舊磚頭的區別僅僅是第一位數字能不能和后面五位數字相同.我們先考慮第一位,后面的數位都不能屬于第一位所在的分組.我們現在不妨把第一位所在的分組去掉,只留下九個分組.條件沒有對后五位做出任何限制,這和例題是完全一樣的題型,完成了問題的轉化.得到后五位的排法一共有95種,又第一個數位可以屬于10個分組中任意一個.
10×95=590 490(種).
答:一共有590 490種.
評注:在實際教學中,最好引導學生完成這樣的轉化過程,建立題目之間的聯結,滲透轉化的數學思想.數學解題教學中應著重訓練學生一題多解、多題一解的能力.
筆者借助一道形式上與例題完全不同的高考題來完成最后的“引玉”.
(三)引 玉
(2012江蘇20)設集合Pn={1,2,…,n},記f(n)為同時滿足下列條件的集合A的個數:①A?Pn,②若x∈A,則2x?A;若x∈PnA,則2x?PnA.
(1)求f(4);
(2)求f(n).
解:(1)f(4)=4(略去過程).
(2)分析:我們先研究所有的奇數,再研究所有的偶數.
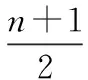
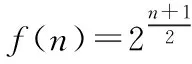
評注:讀者不難感受到玉和磚是如此的形不似神似,每個奇數都可以獨立選擇兩個分組,就像例1中每個數位上都可以獨立選擇十個“分組”.只不過多了能判斷確定位置的偶數.我們把這樣難度的高考題和非常簡單的例1建立聯結,從而大大簡化一道復雜問題的求解,會驚嘆多題一解的威力.兩道看上去風馬牛不相及的題目,卻有著完全相同的實質.這道“簡單”的高考壓軸題其實卻一點不簡單,學生極少有能做出來的.教師平時要注重多題一解的訓練.
三、“三國演義”
說到多題一解,那么對于不同類型的排列組合問題,我們是否能有一種好方法能找到一般的順序呢?
我們假定只有這么三類元素:
①如果把它們按順序取出,后者可以選擇除了前面元素的取法之外的其他所有取法;
②他們之間彼此完全獨立地選擇除了第一類元素選法之外的所有取法;
③前面兩類中的某一個元素一旦確定選法,則該元素只有一種取法.
下面對于只含有如上三類元素的排列組合問題給出一個比較好的順序.
假定有k個第一類元素,p個第二類元素,若干個第三類元素,每個元素最多有m種選擇(k 第一步:按照順序,先把所有的第一類元素取出,再把所有的第二類元素取出,最后把所有的第三類元素取出. 第二步:先按照一種排法把第一類元素先選,一定會占據k個位置,把這些位置去掉繼續考慮. 第三步:考慮第二類元素在剩下m-k個位置中的排法,根據分步計數原理共有(m-k)p. 回過頭來我們驗證前面的兩道題目: 借助多題一解的視角,一些看似不同類型的問題,卻可以有統一的程序化步驟和一般的公式.也許,還有涵蓋范圍更為一般的統一公式值得我們進一步探索. 筆者覺得所謂多題一解最重要的核心是轉化與化歸的數學思想.建議讀者平時可多注意各章節的聯系,打通各章節,也許我們還會有更多類似的發現:原來很多形式上不同的題本質上是一致的,有著類似的,甚至是統一的解法.這樣,一道復雜的題原來和一道簡單的題是“差不多”的.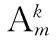
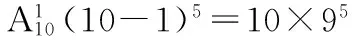
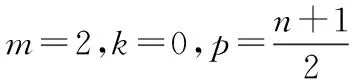

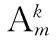
四、結 語

