例談對(duì)數(shù)函數(shù)中的典型錯(cuò)解及教學(xué)建議
◎吳小麗
(西華師范大學(xué),四川 南充 637002)
例談對(duì)數(shù)函數(shù)中的典型錯(cuò)解及教學(xué)建議
◎吳小麗
(西華師范大學(xué),四川 南充 637002)
對(duì)數(shù)函數(shù)是高中數(shù)學(xué)學(xué)習(xí)的一種重要函數(shù),函數(shù)本身就綜合性、抽象性強(qiáng),對(duì)于高一學(xué)生剛接觸到此種新型函數(shù),難免會(huì)出現(xiàn)各式各樣的錯(cuò)誤,研究解題中的錯(cuò)誤、充分發(fā)揮錯(cuò)解的潛在功能,對(duì)于提高教學(xué)質(zhì)量是十分有意義的.
對(duì)數(shù)函數(shù);錯(cuò)解;教學(xué)建議
一、忽視定義域而導(dǎo)致解題出錯(cuò)
(一)利用單調(diào)性解不等式
例1 已知函數(shù)f(x)=lg(x+1),解關(guān)于x的不等式0 (二)復(fù)合函數(shù)中的單調(diào)性與最值 例2 若y=loga(2-ax)在[0,1]上是減函數(shù),則a的取值范圍是________. 錯(cuò)解分析 大部分學(xué)生一看到底數(shù)是字母a,立刻想到分類(lèi)討論,復(fù)雜易錯(cuò),還有很大一部分學(xué)生忽視了定義域?yàn)閇0,1],在[0,1]上要真數(shù)大于0. 正解 ∵a>0,∴-a<0,∴u=2-ax在[0,1]上為減函數(shù).又∵y=loga(2-ax)在[0,1]是減函數(shù),∴y=lgau在[0,1]為增函數(shù),即a>1且2-a×1>0,∴1 例3 已知f(x)=2+log3x,x∈[1,9].求函數(shù)y=[f(x)]2+f(x2)的最大值及y取得最大值時(shí)的x的值. 錯(cuò)解分析 大部分學(xué)生能夠得出y=(log3x+3)2-3,令t=log3x,則y=(t+3)2-3,但直接認(rèn)為定義域就為[1,9],從而得到t∈[0,2],進(jìn)而得到錯(cuò)誤答案.其實(shí)由1≤x≤9且1≤x2≤9得,函數(shù)y的定義域?yàn)閇1,3],從而t∈[0,1].用到換元時(shí),一定要注意新元的取值范圍,因此,正確求得復(fù)合函數(shù)的定義域顯得尤為關(guān)鍵. 例4 (1)已知函數(shù)y=log2(x2-2kx+k)的值域?yàn)镽,則k的取值范圍為_(kāi)_______. (2)已知函數(shù)y=log2(x2-2kx+k)的定義域?yàn)镽,則k的取值范圍為_(kāi)_______. (1)錯(cuò)解 由題意,x2-2kx+k>0在R上恒成立,所以Δ=4k2-4k<0,即0 正解 由題意,在定義域內(nèi),真數(shù)x2-2kx+k能取得所有大于0的值,所以Δ=4k2-4k≥0,即k∈(-∞,0]∪[1,+∞). (1)的錯(cuò)解即為(2)的正解. 錯(cuò)解分析 在R上為增函數(shù),很多學(xué)生考慮不全面,只考慮到每段為增,還要保證整體單調(diào),即要考慮在分段點(diǎn)處的大小關(guān)系.實(shí)際上是學(xué)生對(duì)單調(diào)性的概念沒(méi)有真正理解. 根據(jù)學(xué)生在對(duì)數(shù)函數(shù)相關(guān)習(xí)題中的錯(cuò)解,可以發(fā)現(xiàn)大多數(shù)是因?yàn)閷?duì)數(shù)函數(shù)的相關(guān)概念理解不透,其次,不能運(yùn)用數(shù)形結(jié)合等數(shù)學(xué)思想方法來(lái)分析題意,數(shù)學(xué)思維能力比較薄弱.對(duì)此,提出以下幾點(diǎn)教學(xué)建議.(1)數(shù)學(xué)學(xué)習(xí)中,概念學(xué)習(xí)是基礎(chǔ),教師應(yīng)注重?cái)?shù)學(xué)概念的教學(xué).將抽象的數(shù)學(xué)概念與生活實(shí)際相結(jié)合,做到循序漸進(jìn),一點(diǎn)一點(diǎn)強(qiáng)化.(2)應(yīng)加強(qiáng)學(xué)生作圖的訓(xùn)練.很多題只要能快速畫(huà)出草圖,就能使本身抽象難懂的題目變得簡(jiǎn)潔易懂,思路也會(huì)開(kāi)闊許多,從而使解題更快捷簡(jiǎn)便.(3)應(yīng)加強(qiáng)數(shù)學(xué)思想方法的滲透.讓學(xué)生了解更多數(shù)學(xué)思想方法,可以從多角度去思考問(wèn)題.(4)加強(qiáng)學(xué)生數(shù)學(xué)思維能力的培養(yǎng).很多高一學(xué)生數(shù)學(xué)思維還停留在初中,對(duì)于一些難度稍大的題目便束手無(wú)策,教師應(yīng)適當(dāng)引導(dǎo),加強(qiáng)對(duì)其數(shù)學(xué)思維能力的培養(yǎng),使其能更深地思考問(wèn)題進(jìn)而提高學(xué)習(xí)能力. [1]鄭云霞.對(duì)數(shù)函數(shù)常見(jiàn)解題誤區(qū)[J].中學(xué)生數(shù)理化(高一版),2011(22):17. [2]王海清.發(fā)揮錯(cuò)解潛在功能 提高數(shù)學(xué)教學(xué)質(zhì)量[J].湖州師范學(xué)院學(xué)報(bào),1998(5):74-81.二、混淆定義域與值域而導(dǎo)致解題出錯(cuò)
三、對(duì)分段函數(shù)的單調(diào)性考慮不全而出錯(cuò)
四、不能數(shù)形結(jié)合而導(dǎo)致解題困難
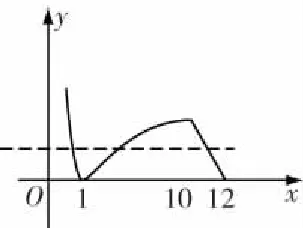
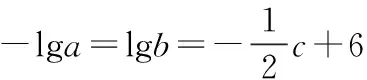
五、教學(xué)建議
 數(shù)學(xué)學(xué)習(xí)與研究2017年9期
數(shù)學(xué)學(xué)習(xí)與研究2017年9期
——從“數(shù)學(xué)悖論”的消除中發(fā)現(xiàn)數(shù)學(xué)潛在的和諧美
——“概率與統(tǒng)計(jì)”
——以證明兩線垂直為例
