從一道高考題談平面向量數(shù)量積問題處理的兩種常見策略

◎朱麗娟

(江蘇揚(yáng)州大學(xué)附屬中學(xué)東部分校，江蘇 揚(yáng)州 225002)

從一道高考題談平面向量數(shù)量積問題處理的兩種常見策略

◎朱麗娟

(江蘇揚(yáng)州大學(xué)附屬中學(xué)東部分校，江蘇 揚(yáng)州 225002)

平面向量是高中數(shù)學(xué)新課程新增內(nèi)容，也是高考重點(diǎn)考查的知識(shí)點(diǎn).在各省及全國(guó)高考中都有出現(xiàn).下面就2016年江蘇高考題第13題為例，談數(shù)量積問題處理的一般策略.

高考題；平面向量數(shù)量積；策略

策略一：基底法

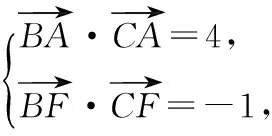
分析 平面向量基本定理告訴我們，平面中兩個(gè)不共線的向量可作為一組基底，對(duì)于平面中的任意一個(gè)向量都可由這兩個(gè)基底向量唯一線性表示.

一般來(lái)說(shuō)，基底的選擇主要有三個(gè)原則：一是已知條件中已經(jīng)出現(xiàn)的向量；二是已知長(zhǎng)度和角度的向量；三是表示所需向量較為容易的向量.

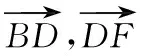
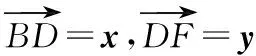
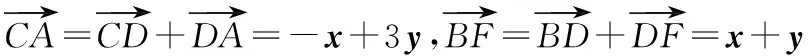
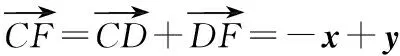
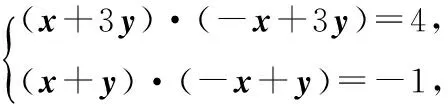
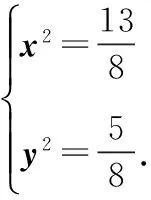
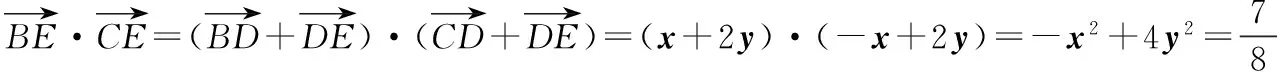
策略二：坐標(biāo)法

分析 對(duì)于規(guī)則圖形如直角三角形以及含直角的多邊形、等腰三角形，學(xué)生易想到用建系設(shè)點(diǎn)的方法表示已知、未知向量，從而解決問題.但有些題目，雖然沒有明顯的直角或?qū)ΨQ關(guān)系，也可以利用坐標(biāo)法，設(shè)出必要參數(shù)解決問題.

本題中，條件是：在△ABC中，D是BC的中點(diǎn)，E，F(xiàn)是AD上的兩個(gè)三等分點(diǎn)，故可以以D為坐標(biāo)原點(diǎn)建系，設(shè)出點(diǎn)A的坐標(biāo)，再表達(dá)出點(diǎn)E，F(xiàn)的坐標(biāo).

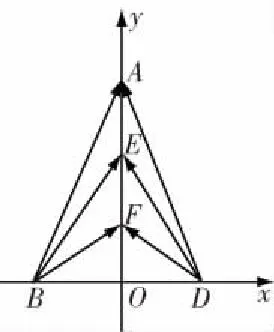
解 以D為坐標(biāo)原點(diǎn)，BC所在直線為x軸，建立如圖所示的直角坐標(biāo)系.

設(shè)B(-a，0)，C(a，0)，A(3x，3y)，則E(2x，2y)，F(xiàn)(x，y).

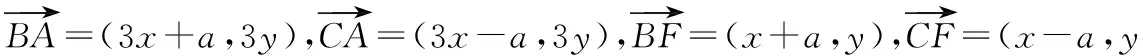
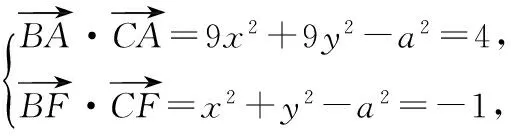
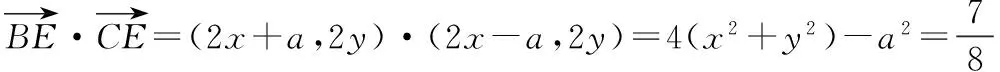
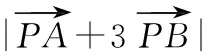
基底法和坐標(biāo)法是處理平面向量數(shù)量積的兩種常見策略，在很多問題求解中，這兩種方式都可以方便地求出結(jié)果.學(xué)生們?cè)诰唧w的解題和臨考發(fā)揮中，選擇什么方法一擊即中，需要在平時(shí)的練習(xí)中多思考和總結(jié).