數學美的和諧性研究之一
——從“數學悖論”的消除中發現數學潛在的和諧美

◎曾瑞海

(汕頭職業技術學院，廣東 汕頭 515041)

數學美的和諧性研究之一
——從“數學悖論”的消除中發現數學潛在的和諧美

◎曾瑞海

(汕頭職業技術學院，廣東 汕頭 515041)

本文借助三個數學悖論，從消除悖論的過程中發現數學潛在的和諧美，進而提高認識數學和諧美的目的.

數學悖論；和諧性；連續；無窮小量

盡管各種數學悖論產生的歷史背景不同，表現形式各異，但它們都是某一數學理論原有體系中蘊藏著矛盾的反應.人們面對數學悖論的產生而著手對數學概念進行重塑，對不完善的理論進行改進，進而產生了新的數學觀念，完善了思維方法，推動了數學理論的發展，在更高的層次上實現了新的和諧統一與完善.因此，數學悖論是促使數學理論不斷追求和諧、不斷趨于完善的一種重要的推動力，是給數學的發展帶來新的生機和希望的火種.

由此可見，數學自身顯然是從不和諧走向和諧的.

一、從“連續悖論”的消除中發現數學潛在的和諧美

我們知道，“連續”是高等數學中一個重要的基本概念，但是它的現代定義的表達卻是經歷了一個從不和諧到和諧的漫長過程.

數學家歐拉曾認為，由一個單獨解析表達式給出的函數是連續的，而由幾個表達式給出的函數即分段函數是不連續的.

但我們又知道，傅立葉已經證明，定義在某個區間上的任意函數都可以表示成該區間上的正弦函數與余弦函數的無窮級數.

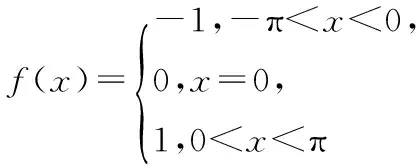
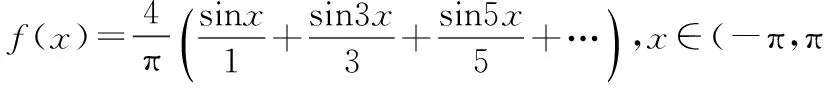
上述函數依照歐拉對連續的定義，既是不連續的，同時，又是連續的.顯然這是一個悖論.

二、從“貝克萊悖論”的消除中發現數學潛在的和諧美

數學史上把貝克萊的問題稱之為“貝克萊悖論”.籠統地說，貝克萊悖論可以表述為“無窮小量究竟是否為0”的問題：就無窮小量在當時實際應用而言，它必須既是0，又不是0.但從形式邏輯而言，這無疑是一個矛盾.

1734年，大主教喬治·貝克萊(George Berkeley)以“渺小的哲學家”之名出版了一本標題很長的書《分析學家；或一篇致一位不信神數學家的論文，其中審查一下近代分析學的對象、原則及論斷是不是比宗教的神秘、信仰的要點有更清晰的表達，或更明顯的推理》.在這本書中，貝克萊對牛頓的理論進行了攻擊.

他指責牛頓，在其理論中，無窮小量一會兒說是零，一會兒又說不是零.

舉例來說，為計算某函數的導數，比如，說x3的導數，先將x取一個不為0的增量Δx，由(x+Δx)3-x3，得到3x2·Δx+3x·(Δx)2+(Δx)3，后再被Δx除，得到3x2+3x·(Δx)+(Δx)2，最后突然令Δx=0，求得導數為3x2.這是“依靠雙重錯誤得到了不科學卻正確的結果”.因為無窮小量在牛頓的理論中一會兒說是零，一會兒又說不是零，因此，貝克萊嘲笑無窮小量是“已死量的幽靈”.貝克萊的攻擊抓住了牛頓理論中的缺陷，是切中要害的.

18世紀粗糙的，不嚴密的工作也導致謬誤越來越多的局面，不諧和音的刺耳開始震動了數學家們的神經.

從1821年開始，柯西陸續出版了幾本具有劃時代意義的書與論文.其中給出了分析學一系列基本概念的嚴格定義.比如，他開始用不等式來刻畫極限，使無窮的運算化為一系列不等式的推導.這就是所謂極限概念的“算術化”.柯西的工作使分析基礎嚴密化邁出了第一大步.

在柯西的努力下，連續、導數、微分、積分、無窮級數的和等概念也建立在了較堅實的基礎上.不過，在當時情況下，由于實數的嚴格理論尚未建立起來，所以柯西的極限理論還不可能完善.

柯西之后，魏爾斯特拉斯、戴德金、康托爾各自經過自己獨立深入的研究，都將分析基礎歸結為實數理論，并于70年代各自建立了自己完整的實數體系.魏爾斯特拉斯的理論可歸結為遞增有界數列極限存在原理；戴德金建立了有名的戴德金分割；康托爾提出用有理“基本序列”來定義無理數.

三、從“蒙提·霍爾悖論”的消除中發現數學潛在的和諧美

問題提出：假設你正在參加一個游戲節目，你被要求在三扇門中選擇一扇.其中一扇后面有一輛車，其余兩扇后面則是山羊.你選擇了一扇門，假設是1號門，然后，知道門后面有什么的主持人開啟了另一扇后面有山羊的門，假設是3號門.然后，他問你：“你想選擇2號門嗎？”那么，改變你的選擇對你來說是一種優勢嗎？

數學少不了悖論，數學公理系統沒有悖論就不是完備的，我們不是去容忍悖論而是去消除悖論，在消除悖論的過程中提高認知水平.數學教學中常常因為悖論的思考復雜性而棄置不用，筆者相信悖論的使用不僅不會增加難度，反而會使問題更富趣味性和研究性，更有利于激發學生對數學學習的興趣；有利于向學生介紹重要的數學思路；有利于開發豐富多彩的數學學習活動；有利于幫助學生洞察數學問題的解題過程；有利于培養學生辯證的、開創性的、批判性的思維方式；有利于提高學生對現代數學所具有的美妙、多樣，甚至幽默性質的鑒賞力.從這個意義上說，沒有悖論的數學學習是危險的，沒有悖論思想的數學教學是蒼白的.數學家同時也是悖論大師，悖論不是目的，以悖論為手段學會創新才是目標.

[1]李雍.數學和諧美[M].大連：大連理工大學出版社，2009.

[2]陶理.關于數學悖論的認識問題[J].東北師大學報(哲學社會科學版)，1993(6):80-84.

[3]王方漢.歷史上的三次數學危機[J].數學通報，2002(5)：42-43.

[4]王秀芳，郝素娥.論數學悖論的思維特色[J].山西大學師范學院學報(綜合版)，1993(2):39-43.

[5]吳振奎，吳旻.數學中的美[M].上海：上海教育出版社，2002.

[6]張媛媛.試論數學的和諧美[J].開封大學學報，2013(2):65-67.