在不同解法的轉換中優(yōu)化學生的思維品質
江蘇省常熟市尚湖高級中學(215500)
江 政●
?
在不同解法的轉換中優(yōu)化學生的思維品質
江蘇省常熟市尚湖高級中學(215500)
江 政●
本文舉例說明了用數(shù)學題的不同解法,可以優(yōu)化學生的思維品質.
不同解法;思維;培養(yǎng)
在培養(yǎng)學生的數(shù)學思維品質方面,除了要重視學生數(shù)學解題能力的培養(yǎng)外,還要通過不的解題方法來優(yōu)化學生的思維品質,使學生在采用不同的解題方法中,能夠運用靈活的方式進行解題,讓學生在思考的過程中,對問題辨析,從而使學生的思維品質得到有效培養(yǎng).
一、重視培養(yǎng)學生的思維廣闊性
對學生進行思維廣闊性的訓練,是培養(yǎng)學生數(shù)學思維能力的有效方法.教師在數(shù)學解題教學過程中提出相應的問題,引導學生對問題進行全方位、深層次的思考,在更廣闊的范圍內(nèi)尋求解題方法,以培養(yǎng)學生的數(shù)學思維廣闊性.
例如:假設△ABC的三邊分別為a,b,c,D位于直線AB上,而且BC=DC.假設AD=d,求證cd=b2-a2,c+d=2bcosA.
分析1 通過上題的提示,學生想到題中的“cosA”時,會利用余弦定理來求證. 在△ABC中,a2=b2+c2-2bdcosA;在△ABC中,a2=b2+c2-2bdcosA.兩式相減得c2-d2(c-d)2bccosA=0③.將③代入可得a2=b2+c2-c(c+d)=b2-cd,因此,cd=b2-a2.
分析2 上題中有“c+d”和“cd”,一些學生會聯(lián)想到采用根與系數(shù)來對結論進行求證.由分析1中的①得出c2-2bcosA·c+(b-a)=0.由上述分析中的②得出d2-2bcosA·d+(b2-a2)=0所以,c和d是方程x2-2bcosA·x+(b2-a2)=0的兩根,由此可得出c+d=2bcosA,cd=b2-a2.

通過以上幾種分析方法,運用三角、幾何和代數(shù)等各種知識,采用不同的解題方法,打開學生的解題思路,使學生的思維視野變得更加開闊,從而培養(yǎng)了學生廣闊的思維品質.
二、從不同解題方法轉換的過程中,培養(yǎng)學生的思維深刻性
在進行數(shù)學解題時,學生思維活動的抽象程度與邏輯水平,能夠充分反映出學生思維活動的廣度和深度.教師在進行數(shù)學課堂教學實踐時,讓學生在解題中進行深度思考,增強思維的參與程度,使學生的思維深刻性得到培養(yǎng).
例如:若f(x)=ax3-3x2+1,且f(x)存在唯一的零點x0,x0>0,求a的范圍.
解法一 先求導f′(x)=3x(ax-2),對a進行分類討論.若a=0,則f(x)=-3x2+1.不合題意,舍去.再對a>0和a<0進行討論,根據(jù)函數(shù)在區(qū)間上的單調(diào)性,并結合圖象,綜上得到a<-2.

通過對這道數(shù)學題的解題環(huán)節(jié)歸納和總結,分析兩種解題方法,第一種是用函數(shù)分類討論求解,第二種是用參數(shù)分離求解.兩種方法雖然不同,但都是將此類問題轉化為函數(shù)與方程問題進行求解.通過分析、總結和歸納,掌握數(shù)學問題的規(guī)律,找到此類數(shù)學題目的共性,根據(jù)這種共性去解決這一類的數(shù)學問題,使學生的思維更具深刻性.
三、采用不同的數(shù)學解題方法,培養(yǎng)學生的思維靈活性
在數(shù)學解題過程中,學生的思維靈活性是其在面對各種數(shù)學問題時,靈活運用各種所學的方法來解答問題的一種思維品質.靈活的思考問題,不僅需要學生具備發(fā)散性思維,還需要教師根據(jù)教學內(nèi)容來靈活的設計一些數(shù)學問題,以此來培養(yǎng)學生的思維靈活性,優(yōu)化學生的思維品質.
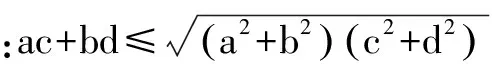


通過以上幾種不同的方法,充分體現(xiàn)了數(shù)學解題方法的多變,以及數(shù)學解題思維所具有的靈活性.而學生在數(shù)學學習中的思維靈活性主要體現(xiàn)在從一種解題途徑,轉為另一種解題途徑時的靈活.除此以外,也可以表現(xiàn)為從已知數(shù)學關系中,發(fā)現(xiàn)新的數(shù)學關系,從數(shù)學題目給出的隱蔽形式中看清數(shù)學問題的實質性特點,而這些能力的獲得都有賴于學生思維靈活性的培養(yǎng).另外,增強學生的思維靈活性,讓學生自如的運用所掌握的思維方法,來分析數(shù)學問題,同時靈活的解決這些數(shù)學問題.
G632
B
1008-0333(2017)15-0005-01

