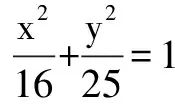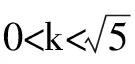數學解題中運用數形結合思想提高創造思維正能量
江蘇省常熟市尚湖高級中學(215500)
孫 丹●
?
數學解題中運用數形結合思想提高創造思維正能量
江蘇省常熟市尚湖高級中學(215500)
孫 丹●
本文指出什么是數形結合思想;數形結合的原則;數形結合的途徑.本文還應用五種題型案例說明數形結合思想在實踐中的應用.
轉化構造;集合中應用;圓錐曲線;三角函數;復數;參數范圍
縱觀科學、藝術和技術發展,它們的共同基礎都是自然的啟示和人類的感情,或被稱作想象力、創造力,兩者缺一不可.藝術,如詩歌、繪畫、音樂等,是創作者將對生命、宇宙、人生的感情通過藝術形式的表現喚起人們的意識或潛意識中深藏著的已經存在的情感;自然科學,如化學、物理、生物等,是用數學公式或自然定律的方式對自然界的現象進行準確的抽象.中國古人常說“文章本天成、妙手偶得之”.古人評價一個好的建筑,講“宛若天成”、“巧奪天工”,評價一個好的手法,叫“神來之筆”,說人的思維在瞬間可以“精鶩八極”、“心游萬刃”、“思接千載”、“視通萬里”,也就是說來源于與宇宙天宇的溝通.北大著名教授朱孝遠說:“我們的創造力,不管它是如何的強大,卻是根基于我們已有的知識和文化中的.也就是蘊藏在我們的歷史之中、時空坐標中,生命的關照總是在最關鍵的時刻,托起人們創新和馴服危機的想象”.
一、數形結合思想
1.所謂數形結合,就是根據數與形之間的對應關系,通過數與形的相互轉化來解決數學問題的一種重要思想方法.數形結合通過“以形助教,以數解形”,使復雜問題簡單化,抽象問題具體化能夠變抽象思維為形象思維,其目的是為了發揮形的生動性和直觀性,數的思路的規范性與嚴密性,二者相輔相成,揚長避短.
數形結合本質:幾何圖形的性質反映了數量關系,數量關系決定了幾何圖形的性質.
2.數形結合的原則
(1)等價性原則.在數形結合時,代數性質和幾何性質的轉換必須是等價的.有時,由于圖形的局限性,不能完整地表現數的一般性,這時圖形的性質只能是一種直觀而淺顯的說明,但它同時也是抽象而嚴格證明的誘導.
(2)雙向性原則.既要進行幾何直觀的分析,又要進行代數抽象的探索,兩方面相輔相成,僅對一方面分析在許多時候是很難行得通的.
(3)簡單性原則.代數問題運用幾何方法,幾何問題尋找代數方法.
3.數形結合的途徑
(1)通過坐標系助解.借助于建立平面直角坐標系、復平面可以將圖形問題代數化.實現數形結合,常與以下內容有關.①實數與數軸上的點的對應關系;②函數與圖象的對應關系;③曲線與方程的對應關系;④以幾何元素和幾何條件為背景,建立起來的概念,如復數、三角函數等;⑤所給的等式或代數式的結構含有明顯的幾何意義.如:等式(x-2)2+(y-1)2=4.
常見方法有:解析法、三角法和向量法.
(2)通過轉化構造數形題解
許多代數結構都有著對應的幾何意義,據此,可以將數與形進行巧妙地轉化,例如,將a>0與距離互化,將a2與面積互化,將a2+b2+a·b=a2+b2-2|a||b|cosθ(θ=60°或θ=120°),與余弦定理溝通,將a≥b≥c>0且b+c>a中的a、b、c與三角形的三邊溝通,將有序實數對(或復數)和點溝通,將二元一次方程與直線、將二元二次方程與相應的圓錐曲線對應,等等,這種代數結構向幾何結構的轉化常常表現為構造一個圖形(平面的或立體的).另外,函數的圖象也是實現數形轉化的有效工具之一,正是基于此,函數思想和數形結合思想經常借助于相伴而充分地發揮作用.
二、數形結合思想在實踐中應用典例
題型一 在集合中應用數形結合思想

例1 設命題甲:0 A.充分不必要條件 B.必要不充分條件 C.充要條件 D.既不充分也不必要條件 解析 將兩個命題用數軸表示,如圖所示,從圖可以看出,命題甲是命題乙的充分不必要條件,故選A. 題型二 在圓錐曲線中應用數形結合思想 題型三 在三角函數、復數中應用數形結合思想 題型四 在解析幾何中的參數范圍中應用數形結合思想 解析幾何中的參數范圍問題,一直是高考的熱門題型.下面以高考解析幾何有關范圍問題為例,給出幾種常用策略. 根據含參數方程表示曲線的幾何特征,數形結合確定參數的范圍. 題型五 常見高考題應用數形結合思想 例5 若過定點M(-1,0)且斜率為k的直線與圓x2+4x+y2-5=0在第一象限內的部分有交點,則k的取值范圍是( ). 除上數形結合外,有沒有其他的解法呢?下面給出本題解答的兩個新視角. 視角一:線性規劃 我們知道,在平面內,一條直線Ax+By+C=0,把平面分成三部分,直線上的點Ax+By+C=0,在直線兩側的點分別使Ax+By+C>0或Ax+By+C<0.因此,若一條線段與已知直線有交點,則線段的兩個端點必在直線的兩側(或有一點在直線上).把兩個端點坐標分別代入直線方程,得積小于等于0(若不交于端點,則不等于0). 視角二:定比分點 直線與線段的交點必是線段AB的內分點,因此,交點P分線段AB的比λ≥0(當P、A重合時取等號).根據λ的取值范圍. 可得以下兩種解法: 從上面的分析可以看出,該高考題不僅考查考生數形結合思想,同時也考查考生對問題的化歸能力和數學知識綜合運用的能力,是一道好題. G632 B 1008-0333(2017)15-0007-02