用“不完全歸納法”解兩道物理高考題
唐山市豐潤區任各莊鎮中學(064012)
董鳳娥 ●
?
用“不完全歸納法”解兩道物理高考題
唐山市豐潤區任各莊鎮中學(064012)
董鳳娥 ●
針對連續作用過程的物理問題用不完全歸納法來解決很有效.本文以全國高考和北京高考試題為例加以說明,以便引起大家的重視.
物理;全國高考;北京高考;不完全歸納法.
眾所周知,對于一個和自然數n有關的命題,如果由n=1命題成立,可推出n=2命題成立;由n=2命題成立,可推出n=3命題成立;依此類推,由n=k-1命題成立,可推出n=k命題成立;這樣就形成了一個無窮的遞推,從而命題對于n≥0或1的自然數都成立.這種推理在數學上叫做“不完全歸納法”(也可以叫做遞推法).有些高考物理試題用這種推理來解決很有效,但必須要有耐心.下面舉例加以說明以便引起大家的重視.

例1 (2007年全國高考)如圖所示,質量為m的由絕緣材料制成的球與質量為M=19m的金屬球并排懸掛.現將絕緣球拉至與豎直方向成θ=60°的位置自由釋放,下擺后在最低點與金屬球發生彈性碰撞.在平衡位置附近存在垂直于紙面的磁場.已知由于磁場的阻尼作用,金屬球將于再次碰撞前停在最低點處.求經過幾次碰撞后絕緣球偏離豎直方向的最大角度將小于45°.
解析 設絕緣小球m的擺線長度為L,由題設可知每次碰撞都發生在最低點且為彈性正碰,規定向左為速度的正方向,第一次碰撞前絕緣小球的速度為v0,碰撞后絕緣小球的速度為v1,金屬球的速度為V1,碰撞前后由動量守恒定律可得:
mv0=MV1-mv1①
碰撞前后由機械能守恒定律可得:

已知M=19m③,
由①②③聯立,解得
根據題意可知,第二次碰撞前絕緣小球的速度為v1,等于第一次碰撞后絕緣小球的速度.設第二次碰撞后絕緣小球的速度為v2,金屬球的速度為V2,
碰撞前后由動量守恒定律可得:
mv1=MV2-mv2
碰撞前后由機械能守恒定律可得:
已知M=19m
同理可得,第三次碰撞前后有,
mv2=MV3-mv3
已知M=19m
以此類推,可求得第n次碰撞后絕緣小球和金屬球的速度分別為
設第一次碰撞前絕緣小球的動能為E0,根據題意可知碰撞前由最高處到達最低處的過程機械能守恒,則有
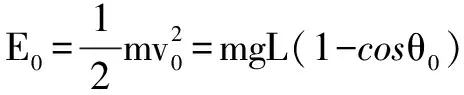
不妨假設,第n次碰撞后絕緣球偏離豎直方向的最大角度等于45°.第n次碰后絕緣球的動能為En,根據題意可知碰撞后由最低處到達最高處的過程機械能守恒,則有
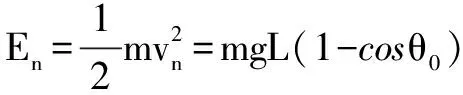


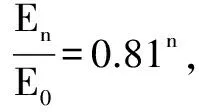
如果經過n次碰撞后絕緣球偏離豎直方向的最大角度小于45°,則有0.81n<0.586
因為,當n=2時,0.586<0.812;當n=3時,0.813<0.586.
所以,經過3次碰撞后絕緣球偏離豎直方向的最大角度將小于450.
例2 (2010年北京高考)雨滴在穿過云層的過程中,不斷與漂浮在云層中的小水珠相遇并結合為一體,其質量逐漸增大.現將上述過程簡化為沿豎直方向的一系列碰撞.已知雨滴的初始質量為m0,初速度為v0,下降距離l后與靜止的小水珠碰撞且合并,質量變為m1.此后每經過同樣的距離l后,雨滴均與靜止的小水珠碰撞且合并,質量依次為m2、m3…mn…(設各質量為已知量).不計空氣阻力.若考慮重力的影響, 求:
(1)第1次碰撞前、后雨滴的速度v1和v1′;

解析 (1)若考慮重力的影響,沿豎直方向(正方向)雨滴下降過程中做加速度為g的勻加速運動,每一次碰撞瞬間(前后)動量守恒.
第1次碰撞后,m0v1=m1v1/

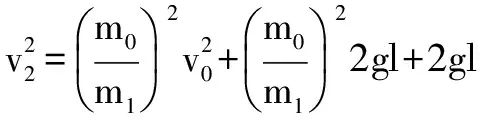

第2次碰撞后,m1v2=m2v2′

結合(2)式可得
依此類推,第n次碰撞后雨滴速度為
所以,第n次碰撞后雨滴的動能為
由以上兩例不難看出,針對連續作用過程的物理問題用不完全歸納法解答很奏效.依托物理問題情景,考查學生運用經典的數學知識和數學思維解決物理問題是今后高考的一種趨勢,希望大家要引起足夠的重視.
[1]http://www.docin.com/p-694276988.html
[2]http://www.docin.com/p-480952069.html
G632
B
1008-0333(2017)13-0079-02

