處理立體幾何問題的常用數學思想

陜西省西安市臨潼區馬額中學(710609)

童永奇●

?

處理立體幾何問題的常用數學思想

陜西省西安市臨潼區馬額中學(710609)

童永奇●

本文擬通過歸類舉例的形式，具體說明處理有關立體幾何問題時經常用到的一些重要的數學思想，旨在幫助讀者拓寬解題思維，進一步提高分析、解決此類問題的實際能力.

類型一、轉化思想

轉化既是一種思想，又是一種策略，也是一種方法.對一個數學問題，經過分析思考后，認為需要轉變成另一個數學問題，這就是轉化思想.轉化思想的實質就是“尋求聯系，實現轉化”.

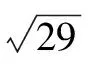
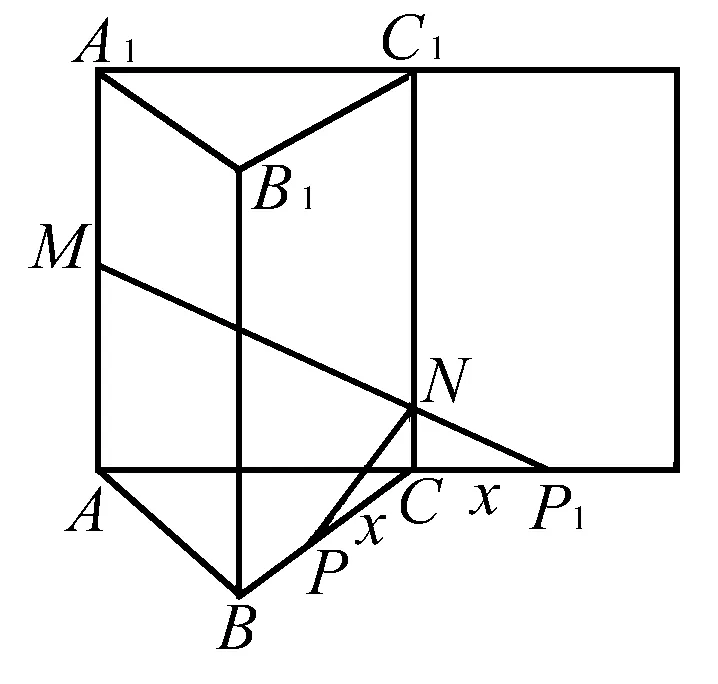
(Ⅰ)求該三棱柱的側面展開圖的對角線長；

(Ⅱ)求PC和NC的長.

分析 第一問比較簡單，根據正三棱柱的側面展開圖為矩形即可獲解；第二問的難點在于，準確分析最短路線對應的具體情景——可借助側面展開圖，將空間中的最小值問題等價轉化為平面中的最小值問題，以便靈活利用平面幾何知識加以思考.

(Ⅱ)如圖，將側面BB1C1C繞棱CC1旋轉120°，使其與側面AA1C1C在同一平面內，此時點P運動到點P1的位置，連接MP1，則易知MP1就是由點P沿棱柱側面經過棱CC1到點M的最短路線.

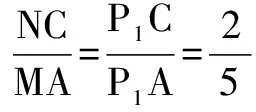
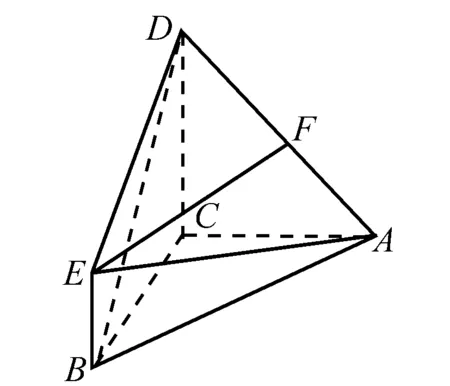
(Ⅰ)求證：EF∥平面ABC；

(Ⅱ)求證：平面ACD⊥平面BCDE；

(Ⅲ)求直線BD與平面AED的夾角θ的正弦值.

分析 第一問考慮直線與平面平行的判定定理可知，欲證直線與平面平行，即證直線與直線平行；第二問考慮平面與平面垂直的判定定理可知，欲證平面與平面垂直，即證直線與平面垂直；第三問考慮空間向量法可知，欲求線面夾角的正弦值，即求直線的一個方向向量與平面的一個法向量的夾角的余弦值.

又EF?平面ABC，BM?平面ABC，故由線面平行的判定定理，得EF∥平面ABC.

∴AC2+BC2=AB2，

∴AC⊥BC.

∵CD⊥平面ABC，AC?平面ABC，∴CD⊥AC.

于是，由BC∩CD=C及線面垂直的判定定理，得AC⊥平面BCDE.

又AC?平面ACD，故由面面垂直的判定定理，得平面ACD⊥平面BCDE.

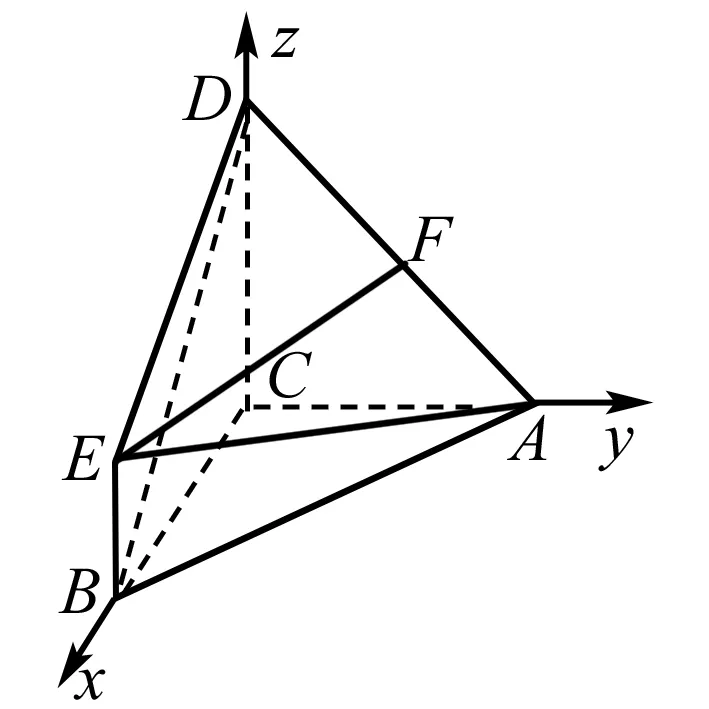
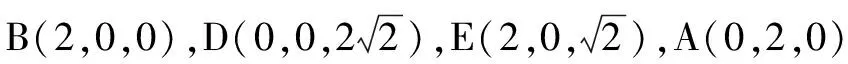
設平面AED的法向量n=(x,y,z)，則

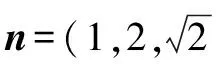
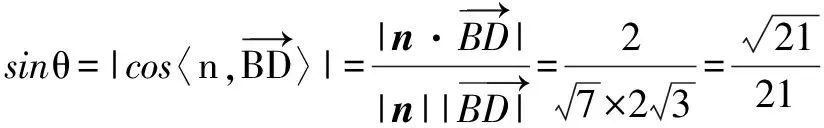
評注 本題主要考查立體幾何中線面平行、面面垂直的判定定理和空間向量法，突出地體現了“轉化思想”在分析、解決問題中的靈活運用.

類型二、分類與整合思想

分類與整合思想是指當問題所給的對象不能進行統一研究時，就需要對研究對象按某個標準進行分類，對每一類分別研究得出每一類的結論，最后綜合各類結果得到整體問題的解答.實質上，分類與整合是“化整為零，各個擊破，再積零為整”的數學解題策略.

分析 由于球心O與正三棱錐A-BCD的位置關系不確定，所以本題應分情況加以討論.為了便于分析求解，在每種情況下需要先畫出圖形，并通過適當作輔助線構造直角三角形.

解析 設正三角形△BCD的中心為H，作截面ABH.

由球心O與正三棱錐A-BCD位置關系的不同可分為以下兩種情況：

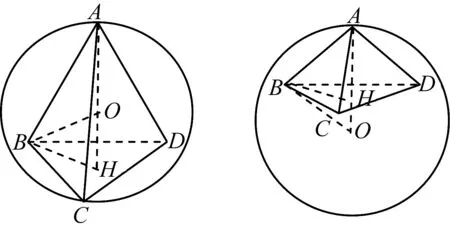
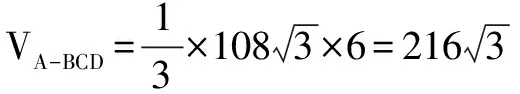
評注 從解題目標看，難點是計算錐體的高，而在求高的過程中，必須注意圖形的不確定性，突出地體現了“分類與整合思想”在分析、解決問題中的靈活運用.

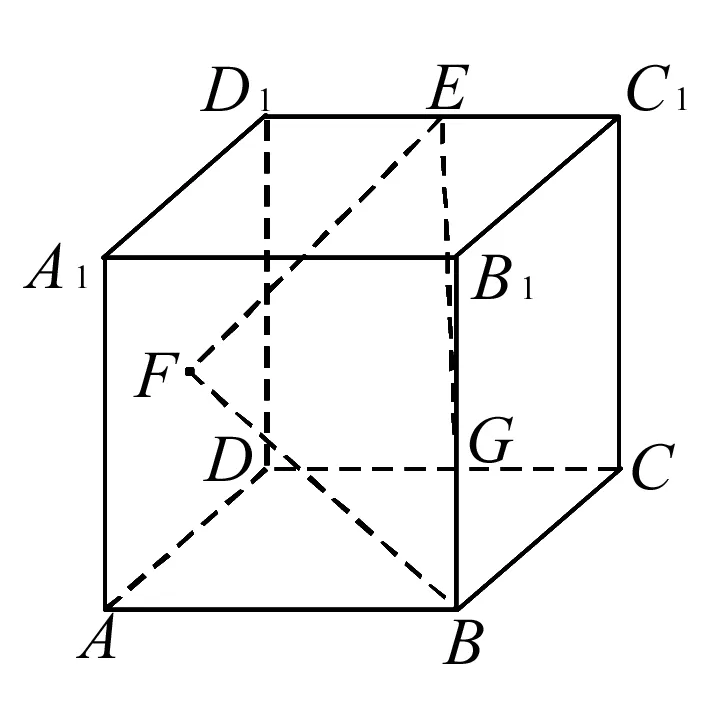
例4 如圖，在棱長為1的正方體AC1中，E、G分別為棱C1D1、BB1的中點，點F是正方形AA1D1D的中心，則空間四邊形BGEF在正方體的六個面內的射影所構成的圖形的面積中的最大值是____．

分析 為了便于求解射影面積的最大值，就必須分別求出空間四邊形BGEF在正方體的六個面內的射影所構成的六個圖形的面積.考慮正方體的對稱性，只需求出三個相鄰面內的射影.

解析 結合正方體的對稱性可知，考查空間四邊形BGEF的射影面積可分以下三種情況：

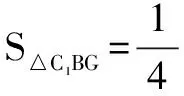
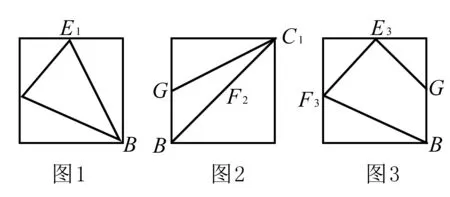
評注 注意到本題以特殊的幾何體“正方體”為載體設置而成，可以大大降低分類討論的過程，優化解題思維，突出地體現了“分類與整合思想”在分析、解決問題中的靈活運用.

類型三、數形結合思想

數形結合思想，就是在研究問題的過程中，注意把數和形結合起來考查，斟酌問題的具體情形，把圖形性質的問題轉化為數量關系的問題，或者把數量關系的問題轉化為圖形性質的問題，使復雜問題簡單化，抽象問題具體化，化難為易，獲得簡便易行的成功方案．

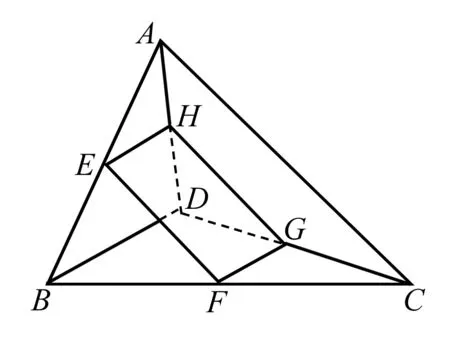
例5 如圖，要在呈空間四邊形形狀的支撐架上安裝一塊矩形太陽能吸光板，矩形EFGH的四個頂點分別在空間四邊形ABCD的邊上.已知AC=a，BD=b，問E、F、G、H在什么位置時，吸光板的吸光量最大.

分析 從目標問題看，要滿足吸光板的吸光量最大，即應滿足矩形EFGH的面積最大.于是，可從“數”的角度出發，先得到該面積的表達式，再具體分析何時面積取得最大值即可順利獲解.

解析 設EH=x，EF=y，因為EH∥FG，EH?平面ABD，FG?平面ABD，所以FG∥平面ABD.又FG?平面BCD，平面BCD∩平面ABD=BD，所以FG∥BD.同理可證EF∥HG∥AC.

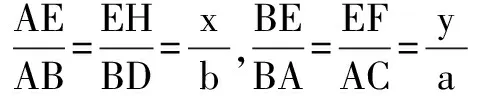
故當E、F、G、H分別為AB、BC、CD、AD的中點時，吸光板的吸光量最大.

評注 本題求解的關鍵是首先充分利用圖形，巧妙地給出矩形EFGH面積的表達式，然后再利用均值不等式確定該面積何時取得最大值.這種解法的優點是將立體幾何問題代數化，便于從“數”的角度加以研究，突出地體現了“數形結合思想”在分析、解決問題中的靈活運用.

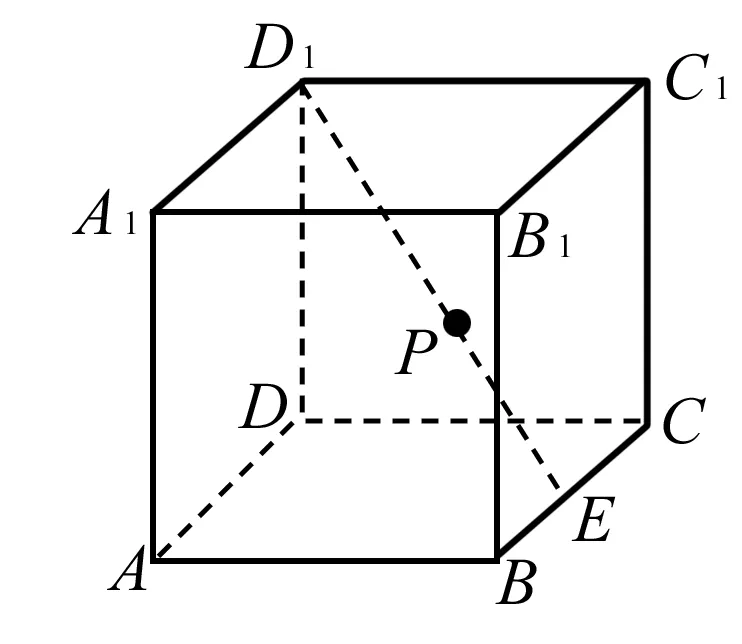
例6 如圖，在棱長為2的正方體ABCD-A1B1C1D1中，E為BC的中點，點P在線段D1E上，點P到直線CC1的距離的最小值為____.

分析 從正方體出發，很容易想到建立空間直角坐標系，進而考慮空間向量法，于是可從“數”的角度出發，先得到點P到直線CC1的距離的解析表達式，再具體分析最小值即可順利獲解.

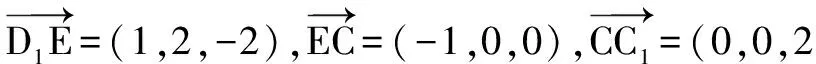
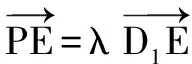
于是，

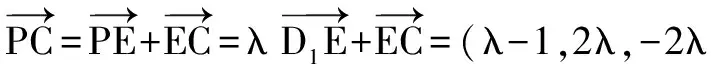
又直線CC1的一個單位方向向量

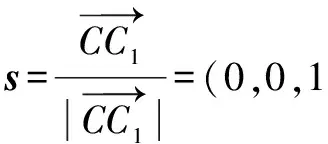
從而，點P到直線CC1的距離為

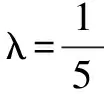
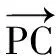
綜上，由于數學思想方法是高考考查的重點，所以我們在解題時應學會有意識地去考慮常用數學思想方法，不斷積累解題經驗，逐步提升解題技能.

G632

B

1008-0333(2017)13-0021-03