論恒成立問題的解題策略

江蘇省昆山市第一中學(215300)

陳小麗●

?

論恒成立問題的解題策略

江蘇省昆山市第一中學(215300)

陳小麗●

本文緊扣住恒成立問題的解題策略這條主線，從四個方面總結了恒成立問題在各個知識板塊的相關應用及應用技巧，并結合了一些實例來具體說明.通過研究發現巧妙運用等價轉化的思想方法可以解決一些具體的數學問題，可起到事半功倍的效果.

恒成立；構建函數；變量分離；數形結合

高中數學中的恒成立問題一直以來都是一個重點、難點，近年來已經逐漸成為高考中的必考題型.這類問題通常題設中均含有恒成立的條件，給我們以很明顯的提示，我們在處理的時候主要是運用等價轉化的數學思想去解決.

恒成立問題包括函數的不同題型，比如一、二次函數；指、對數函數；冪函數以及函數的導數，三角函數的圖象與性質等，還有數列，解析幾何等不同的知識點，順應了考試命題的制定原則.就是因為恒成立問題所涉及的知識點多，有著一定的綜合性，大量學生對怎么樣從試題中獲取知識通常是十分模糊的，進而逐漸變成高中階段學習過程中經常見到的題目.恒成立問題的大量題目均和函數的最值有著一定關系，這就促使教師在日常教學過程中需要向高中學生教授函數的重要思想與方式，不斷指引他們深入了解知識點間存在的關聯，還有教學過程中的通性通法.

為了能夠對于恒成立問題的解題方式有更加全方位的了解，文章嘗試對這些問題的解題方式進行歸納.

一、構造函數，利用函數性質解決恒成立問題

在處理涉及多元不等式恒成立題目的時候，最為主要的就是建立適宜的函數，之后借助其圖象與特征來求解.在涉及多變元的題型中，我們必須按照已知的知識點來明確適宜的變量與數值，來代表存在的函數關系，使題目看起來更加明確.通常而言，必須把已知的條件當作是變量，將需要求解的量當作是參數.

1.變更主元，建立一次函數

大家都知道，一次函數的圖象是一條直線，如果想要使其在范圍內恒大于(或小于)零，僅僅需要讓其在范圍內的兩個端點處恒大于(或小于)零就行.

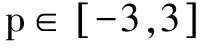
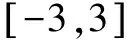
2.構建二次函數

二次函數是高中數學的一個重點，二次函數的恒成立問題主要根據二次函數的圖象與性質來研究，若二次函數y=ax2+bx+c(a≠0,x∈R)的函數值大于零恒成立，我們一般可以考慮用判別式法，只需考慮該函數圖象的開口方向和判別式，其它問題可作類似的處理；若二次不等式中x的取值范圍有限制，則可利用實根的分布來解決問題.根據給定的定義域，一元二次不等式恒成立問題常見下面兩種題型：

分析 由題設可將問題轉化為不等式mx2+2x+3>0對x∈R恒成立，這是一個不等式恒成立問題.設f(x)=mx2+2x+3，由于二項式系數為參數m，所以要先對參數m進行討論，考查了分類與整合思想.當m≠0時，要使不等式恒成立，則對應的二次函數的圖象必須恒在x軸上方，那么我們根據圖象得知開口向上且對應的Δ<0.在本題中，主要貫穿了函數與方程思想及化歸與轉化思想.

例3 對任意x∈[-1,1]，不等式x2+(m-4)x+4-2m>0恒成立，求m的取值范圍.

分析 本題是不等式在給定區間上的恒成立問題.我們可以根據不等式構造出二次函為f(x)=x2+(m-4)x+4-2m，從而問題轉化為二次函數在給定區間上求最小值.我們發現這是常見的動軸定區間問題，于是我們還要根據二次函數的對稱軸與所給區間的相對位置分為三種情況去討論，從而問題得以解決.

3.構建三次函數解決含雙變量的恒成立問題

在上面的兩類問題的討論中我們只涉及了一個變量，一個參數.然而，高中數學關于恒成立的問題拓展的范圍很廣，很深.有很多問題會涉及到多個變量，那么我們在處理這類恒成立問題時就需要先理清楚變量的先后順序，一旦先鎖定一個變量，那么就將問題轉化為這個變量的恒成立問題，運用適當的方法加以解決.下面來看一個實例：

例4 已知f(x)=-x4-ax3-2x2+16lnx+b，其中a,b∈R，若對任意a∈[-2,2]，f(x)≤-x4在x∈(0,1]上恒成立，求實數b的取值范圍.

二、參變量分離，轉化為最值解決恒成立問題

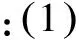
三、數形結合，直觀處理恒成立問題

數形結合就是以形助數，以數輔形，充分利用這種結合，尋找解題思路，在含有不等式恒成立題型中它同樣發揮著十分關鍵的作用.眾所周知，函數圖象與不等式存在一定關系，假設不等式中表示的函數的圖象能夠簡單描繪出來，就能夠借助圖象的位置關聯構建不等式，進而獲得參數區間.

分析 本題中的不等式對應的參數在底數的位置上，不易變形出來.通常我們解答時是將不等式進行變形，使變形后的不等式的兩邊對應的函數為我們所熟悉的基本函數，然后通過作出它們的圖象，通過它們的交點情況來建立相關的不等式進行解答．利用數形結合法解答此類不等式的關鍵有三處：

(1)不等式的變形，找準相應的基本函數；

(2)準確畫出對應函數的有關圖象；(3)尋找兩個圖象的交匯處與位置關聯.

恒成立問題的題型通常包括大量的知識點，求解的方式是較多的，有著十分強大的技巧性，在解題過程中可能還會滲透進分類討論思想，數形結合思想等，這就要求學生具有較強的思維靈活性和創造性.上面我們提到的幾種解題策略是比較常用的，但因為問題的形式千變萬化，考題也常考常新，所以我們要在教學過程中歸納總結出解決恒成立問題的其他方法.我們了解到，解題方式并不是獨立存在的，在求解過程中，通常必須進行綜合考量，自由使用，才可以更加順暢的求解.不過，無論是使用什么樣的求解方法，均融入了教學的思想方式，也就是借助化歸到函數求其最值來進行解決.只有把握了這點，才可以以“不變應萬變”，不過這是需要我們進行深入體驗與歸納.

[1]查志剛.談恒成立問題的求解方法探討[J].數學通報，2003(6).

[2]金建軍.高中數學中的恒成立問題[J].中學教研(數學)，2006.

[3]楊金全.高考數學中的恒成立問題的應用與探究[J].學周刊，2015(12).

G632

B

1008-0333(2017)13-0037-02