淺談高中函數定義域與值域的求法

江西省井岡山中學(343600)

賀 敬●

?

淺談高中函數定義域與值域的求法

江西省井岡山中學(343600)

賀 敬●

函數是高中數學中的重要內容之一，同時也是高考的必考內容.函數由定義域、對應法則、值域三個基本要素組成，而掌握這三要素是理解掌握初等函數這一內容的關鍵.下面分別對函數定義域和值域的一些常見求法進行歸納分析，以便學生和教師參考學習.

函數;數學方法;定義域;值域

一、函數定義域的求法

定義域是函數的必不可少的內容，也是函數值域變化的基礎，依據函數定義域為出發按照對應法則就能夠確定函數的值域.在解答函數的有關問題時，若能把握住定義域的變化，則可提高解題效率.

求初等函數的定義域,限制因素可考慮如下：

(1)若函數出現分式形式，則分母要求不為零 .

(2)如果函數帶有根號，偶次根式的被開方要滿足非負.

(3)若函數中含有對數形式，其真數部分要求非負數.

(4)y=tanθ中，θ≠kπ+π/2,k∈Z.

(5)x0中x≠0等.

1.直接求定義域問題

解 要使函數有意義，必須：5-x2≥1,

解得-2≤x≤2.

2.定義域的逆向問題(已知定義域求參數問題)

定義域是R，求實數a的取值范圍.

(1)當a2-1=0且a+1≠0時，a=1，此時f(x)=1,定義域是R.

a2-1≠0時，有

∴綜上所述，當x∈R時，使得f(x)有意義的a的取值范圍是[1,9].

3.復合函數定義域問題

例3 若函數f(x)的定義域為[-1，1]，求函數f(3x-1)的定義域.

解 因為函數f(x)要滿足x在[-1，1]內取值，函數才有意義，則函數f(3x-1)必需也要求函數自變量3x-1在 [-1，1]內取值，即-1≤3x-1≤1,解出x的取值范圍[0，2/3]就是復合函數的定義域.

二、函數值域的求法

函數的值域是指當自變量取遍定義域上的每一個值時，函數值的取值范圍，其幾何意義是對應函數圖象上點的縱坐標的變化范圍.函數的值域是近幾年高考考查的重點內容之一，也是考試的熱點和難點之一，函數值域的求法有很多種，以下是幾種函數值域最常見的求法.

1.單調性法

運用函數的單調性求解函數的值域，此類題型是在得到函數某一具體的或者限制區間上，或求解具體函數定義域的取值范圍，結合這個函數的特定區間增減性，求出其函數在此段區間端點的函數值或者區間內的最值或者極值，經過對比比較，進而可確定這段區間函數的值域.

2.換元法

若函數中出現無理函數或超越函數，可通過換元轉化為簡單函數.

例7 求函數y=sin2x-sinx+1(x∈R)的值域.

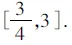
3.判別式法

對于二次分式的值域就可以用判別式法．

解 將函數式去分母，化為關于x的一元二次方程

(y-1)x2-x+(y-1)=0.

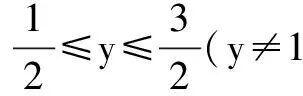
(2)當y=1時，x=0.

4.圖象法

一般用在帶有絕對值符號的函數，先分段表示，再作圖.

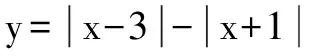
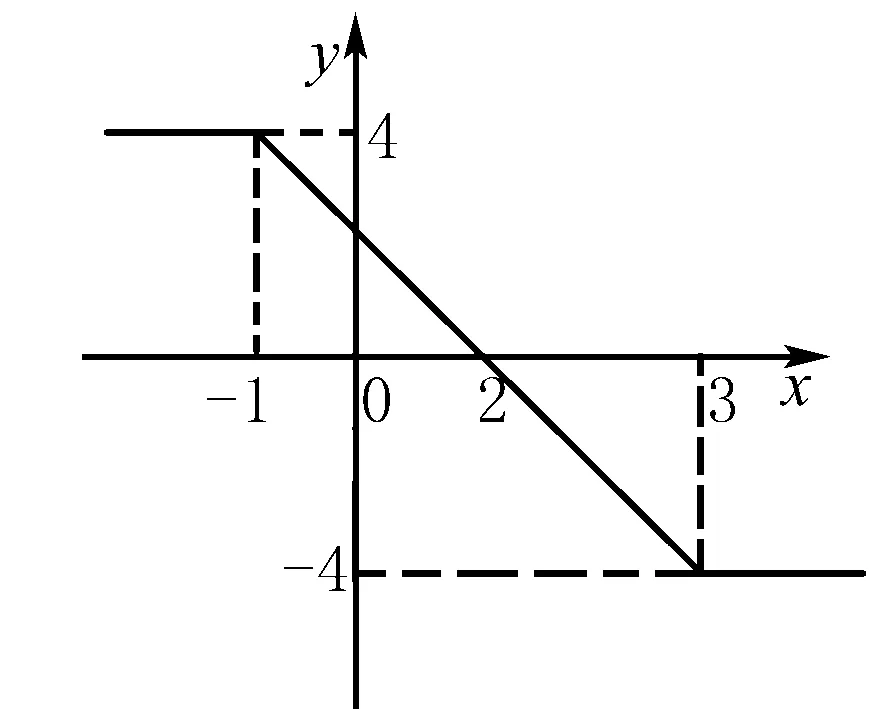
5.分離常數法

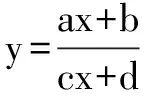
求解高中數學初等函數的定義域和值域問題所涉及的知識面非常廣，方法也是靈活多變，也是近年高考的熱點和難點，因此同學們應該靈活運用方法，多做題訓練，這樣才能收到化繁為簡，事半功倍的效果.

G632

B

1008-0333(2017)13-0041-02