不等式問題證明與思路

湖北省黃石二中(435000)

張熙靈●

?

不等式問題證明與思路

湖北省黃石二中(435000)

張熙靈●

不等式問題、數列問題以及函數問題是歷年高中數學的壓軸大題，其中不等式問題更是進入大學后高等數學難題中的領頭羊.一般而言，不等式問題，解題方法主要有比較法、分析法、綜合法、反證法、放縮法、數學歸納法、換元法、判別式法等十多種方法.本文另辟蹊徑，通過三個例題，從易到難分別介紹構造法、函數法、泰勒級數法在不等式問題中的應用，并對不等式問題的證明方法進行總結，提出針對不等式問題的想法.

不等式；構造法；函數法；泰勒公式

一、構造法證明不等式

構造法證明不等式其實質是將不等式進行等價轉化.借助其他形式，如函數，二次方程的Δ，數列，向量等，通過一系列的數學運算與化簡，把不等式的證明轉換為其他類型函數或方程的求解.如下題，把不等式的證明轉換為二次方程根的存在性，巧妙地避開了直接運算不等式而帶來的復雜計算，為不等式的證明方法提供了一個新的思路.

證明 構造方程(tanγ-2tanα)x2-2(tanαtanβ)x+(2tanβ-tanγ)=0.

1)若tanγ-2tanα=0，因為(tanαtanβ)2≥0，所以原不等式成立.

2)若tanγ-2tanα≠0，當x=-1時，

(tanγ-2tanα)+2(tanαtanβ)+(2tanβ-tanγ)=0，

所以x=-1是方程的根.所以Δ=4(tanαtanβ)2-4(tanγ-2tanα)(2tanβ-tanγ)≥0,所以(tanαtanβ)2≥(tanγ-2tanα)(2tanβ-tanγ).得證.

注：形如B2-AC≥0(或≤0)型不等式可嘗試用構造二次方程來解.

二、函數法證明不等式

所謂函數法，就是從要證明不等式中的某些解析式出發，通過構造一個恰當的函數，并利用函數的性質，完成不等式的證明.其主要的解題思路為，先把不等式化簡，用某一函數代替不等式中復雜部分，然后針對不同類型的函數，根據函數值的有界性或根的存在性求得參量的取值范圍，再通過一系列數學運算最終證明之.

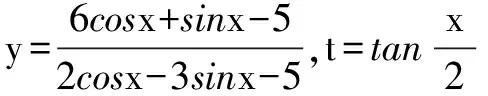
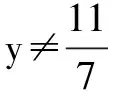
4(3y+1)2-4(7y-11)(3y+1)≥0，從而有： (3y+1)(y-3)≤0 ，

三、利用泰勒級數證明不等式

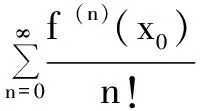
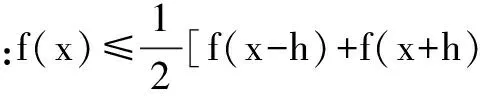
證 由泰勒公式可得(令x0分別為-h與+h)：

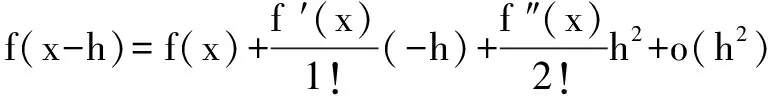
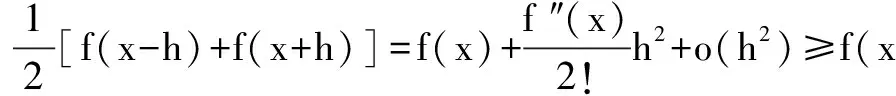
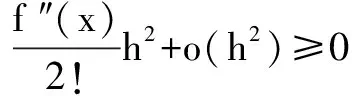
所以，當limh→0 時，f″(x)≥0，命題得證.

[1]胡漢明. 不等式證明問題的思考方法[J].數學通訊，2001(9):22-23．

[2]胡炳生，吳俊. 現代觀點下的中學數學[M]. 北京：高等教育出版社，2001:2118-223.

G632

B

1008-0333(2017)13-0044-01