勻強電場中的二個重要定理
烏魯木齊市教育研究中心(831100)
張萬軍●
?
勻強電場中的二個重要定理
烏魯木齊市教育研究中心(831100)
張萬軍●
本文證明了勻強電場中兩個重要的定理:場中兩點間的的電勢差和兩點間的距離成正比;已知場中確定三點的電勢,場強可唯一確定.進一步通過實例說明定理的應用及拓展.
勻強電場;三點電勢;確定場強
勻強電場是指場中任意一點電場強度的大小和方向都不變的電場,嚴格意義上的勻強電場是不存在的,它是為我們研究方便引入一的一個理想模型,如同勻速運動.
勻強電場的電場線平行等距,等勢面和電場線垂直.“線面垂直”的這一特點為我們解決勻強電場中的問題提供了特有的方法.
下面給出的在勻強電場中的兩個定理及其推論在解決一些與電勢、場強相關的問題中非常有用.
一、定理及證明
定理1 如圖1,勻強電場中AB兩點的距離為L,電勢差為UAB, 則UAB與L成正比,即UAB∝L.
證明:UAB=Ed=ELcosθ∝L
推論:與AB平行等長的線段,其兩端的電勢差與AB兩端的電勢差相等.

由于電勢差和兩點間的距離成正比,是一個線性函數,其圖像是直線,所以,諸如解析幾何這的中點坐標公式,定比分點公式等都可以使用.1999年高考考了這樣一道題目,開創了此類題目的先河.
圖2中A、B、C、D是勻強電場中一正方形的四個頂點.已知A、B、C三點電勢分別為UA=15V,UB=3V,UC=
-3V.求D點的電勢UD.
根據推論,我們有UD-UC=UA-UB,即UD-(-3)=15-3,UD=9V
定理2 已知勻強電場中確定的三點(其確定的平面與電場平行)的電勢,可以求得場強.
推論:已知一點(A)到其他兩點(B、C)的電勢差(UAB、UAC),可以求得場強.
確定的三點意味著三點構成一個確定的三角形.滿足下面任意一個條件,三角形即被確定.已知三邊;已知兩邊及其夾角;已知兩角和任意一邊
證明 為方便,考慮已知三角形兩邊d1、d2、和夾角α的情況.

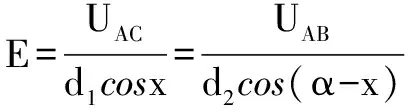
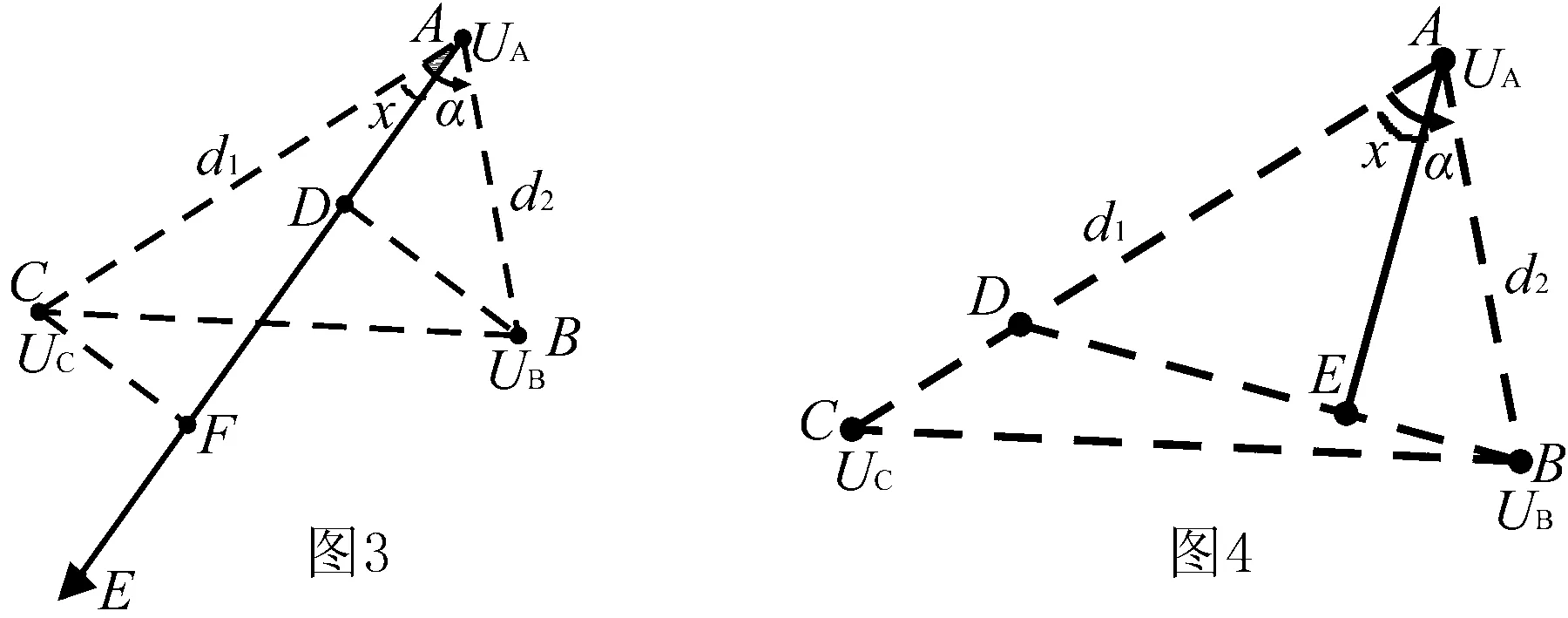
方法二 如圖4,等勢面法確定.(不妨設UA>UB>UC)
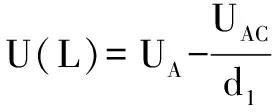
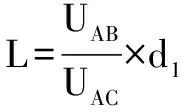
(3)連接BD,過A做BD的垂線AE,AE的方向就是場強的方向.
二、應用
例1 如圖5,勻強電場中有A、B、C三點,∠ACB=90°,AC∶CB=1∶3,一點電荷從C點到A點電場力做功為2 J,從A到B移動的過程中電場力做功為4 J.確定場強方向.

可以設C點電勢為0,點電荷電量為1庫侖.則A點電勢為-2伏,B點 電勢為-6伏.顯然,BC上距C的三分之一BC處D的電勢為-2伏,所以AD為等勢面.過C點與AD的垂線即為場強方向,與AC的夾角為45°.

(1)無電場時,小球到達A點時的動能與初動能的比值;
(2)電場強度的大小和方向.
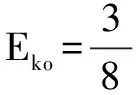
本題的第二問難倒了一批學生.難點之一:多了一個場,是一個復合場問題;難點之二:兩次拋出的方向不確定.這兩個點干擾了學生的思維,他們總覺得少了什么條件.
其實,對兩次拋出的過程使用動能定理后,我們會發現,可以用小球的初動能表示O點到A、B兩點的電勢差.從而使問題迎刃而解.
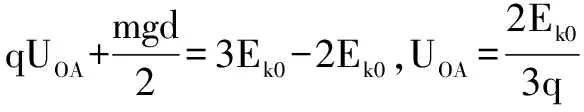

顯然,圖7中,將OB三等分,在二等分的M點,其電勢與A點相同.由幾何關系知,此時OM=OA,AM的垂線恰是△MOA底邊AM上的高,所以α=30°.
即電場方向與豎直向下的方向的夾角為30°.
設場強的大小為E,有qEdcos30°=qUOA
我們看到,在實際問題中,若三點電勢的具體值給出,可以很方便地通過觀察和簡單的計算確定場強的方向,不必按照方法一、二按部就班求解.
三、與數學的聯系

平面直角坐標系有兩個互相垂直的坐標軸,恰好滿足電場線和等勢面垂直的特點.若將一個坐標軸表示電勢,那么另外一個坐標軸的方向就是場強的方向.前面給出的兩個定理可以在這里直接使用.
如圖8,已知平面直角坐標系中A、B、C三點的橫坐標分別為3、4、5,確定坐標原點及x、y軸.

步驟:如圖9.
(1)顯然,A、C中點D的橫坐標為4.連接BD,y軸與BD平行,x軸與BD垂直.
(2)延長CA至E,使AE=3AD,D點就是坐標原點.

(3)過E點做DB延長線的垂線,垂線即為x軸.
(4)過E點做x軸的垂線,垂線即為y軸.
若已知三角形的邊長,還可以求出三點的縱坐標.
四、拓展
(1)若已知三點確定的平面與場強方向不平行,可以將三個點投影到電場線決定的平面上,再用定理二求得場強.
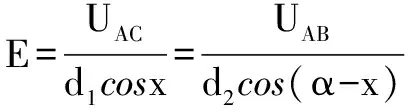
(3)在講兩個定理之前,先做一個已知三點的橫坐標,求坐標系的數學問題是不是對兩個物理定理的理解更好呢?
G632
B
1008-0333(2017)13-0075-02

