BDS/GPS偽距差分改正數(shù)3種內(nèi)插方法的比較
周萬振,秘金鐘,李得海,方書山,陳 振,余夢洋
(1.山東科技大學(xué) 測繪科學(xué)與工程學(xué)院,山東 青島 266590; 2.中國測繪科學(xué)研究院,北京 100830;3.青島市勘察測繪研究院,山東 青島 266000)
?
BDS/GPS偽距差分改正數(shù)3種內(nèi)插方法的比較
周萬振1,2,秘金鐘2,李得海2,方書山2,陳 振3,余夢洋1,2
(1.山東科技大學(xué) 測繪科學(xué)與工程學(xué)院,山東 青島 266590; 2.中國測繪科學(xué)研究院,北京 100830;3.青島市勘察測繪研究院,山東 青島 266000)
針對BDS/GPS融合偽距差分定位中,利用基準(zhǔn)站改正數(shù)生成用戶偽距改正數(shù)的各內(nèi)插方法效率易受用戶與基準(zhǔn)站距離遠(yuǎn)近、基準(zhǔn)站數(shù)量等因素影響的問題,分析當(dāng)基準(zhǔn)站數(shù)不同時,反距離權(quán)重插值法、線性內(nèi)插法和低次曲面模型法等3種內(nèi)插方法用于BDS/GPS融合偽距差分時的定位效率和精度,并提出適合BDS/GPS融合偽距差分定位的最優(yōu)內(nèi)插方法。實驗結(jié)果表明,當(dāng)用戶附近可利用的基準(zhǔn)站數(shù)不少于3站,采用離用戶較近的3個基準(zhǔn)站構(gòu)成多邊形網(wǎng)且用戶在多邊形網(wǎng)內(nèi)時,利用反距離權(quán)重插值法或線性內(nèi)插法生成偽距改正數(shù)來進(jìn)行BDS/GPS融合偽距差分定位,所獲得的定位效率和精度更優(yōu)。
BDS/GPS融合偽距差分定位;反距離權(quán)重插值法;線性內(nèi)插法;低次曲面模型法
0 引言
隨著北斗衛(wèi)星導(dǎo)航系統(tǒng)(BeiDou navigation satellite system,BDS)于2012年底完成亞太地區(qū)組網(wǎng)服務(wù),我國自主導(dǎo)航系統(tǒng)的普及工作已勢在必行[1]。基于多星座的全球衛(wèi)星導(dǎo)航系統(tǒng)(global navigation satellite system,GNSS)偽距差分定位方法相比于單衛(wèi)星系統(tǒng)而言具有更多的可觀測衛(wèi)星、更合理的星座結(jié)構(gòu)等優(yōu)勢[2],正逐步應(yīng)用于交通信息采集、車輛導(dǎo)航定位和車輛控制等增強(qiáng)定位服務(wù)[3]。
內(nèi)插流動站偽距改正數(shù)是網(wǎng)絡(luò)偽距差分定位方法的重要環(huán)節(jié),而流動站與基準(zhǔn)站距離的遠(yuǎn)近、基準(zhǔn)站的數(shù)量都會影響到內(nèi)插方法的效率[4];因此在網(wǎng)絡(luò)偽距差分方法中尋找一種最優(yōu)內(nèi)插方法尤為必要。
本文基于BDS/GPS融合偽距差分定位方法[5-7],選取不同數(shù)量的基準(zhǔn)站分別進(jìn)行解算,并比較分析反距離權(quán)重插值法、線性內(nèi)插法和低次曲面模型法這3種方法的優(yōu)劣。
1 常用內(nèi)插方法數(shù)學(xué)模型
1.1 反距離權(quán)重插值法
反距離權(quán)重插值法是空間位置內(nèi)插方法中較為簡單的一種方法,原理是將各基準(zhǔn)站偽距改正數(shù)的加權(quán)平均值作為流動站的偽距改正數(shù),各基準(zhǔn)站改正數(shù)的定權(quán)方法是根據(jù)改正數(shù)的權(quán)與流動站離基準(zhǔn)站的距離成反比原則[8-10],公式為
(1)
式中:n為采用的基準(zhǔn)站數(shù);Vu為流動站的改正數(shù);Vi為第i基準(zhǔn)站的改正數(shù);φi為內(nèi)插系數(shù);Si為第i基準(zhǔn)站的空間相關(guān)系數(shù),即本文所取流動站到基準(zhǔn)站距離di的倒數(shù);(xi,yi)為第i基準(zhǔn)站的水平坐標(biāo);(xu,yu)為流動站水平概略坐標(biāo)。
該方法內(nèi)插系數(shù)φi的個數(shù)由基準(zhǔn)站數(shù)量決定,并且等于基準(zhǔn)站數(shù),因此存在n個內(nèi)插系數(shù),系數(shù)矩陣表示為
Φ={φ1,φ2,φ3,…,φn}。
(2)
反距離權(quán)重插值法是在基準(zhǔn)站和流動站位置已知的情況下,通過計算流動站與各基準(zhǔn)站之間水平距離而定的權(quán),這在一定程度上可以顧及位置對差分改正數(shù)的影響。由于該方法有模型簡單、計算機(jī)語言易于實現(xiàn),且不受基準(zhǔn)站數(shù)量限制等優(yōu)點;因此當(dāng)局域范圍內(nèi)基準(zhǔn)站數(shù)量有限時,該方法較為適合。
1.2 線性內(nèi)插法
線性內(nèi)插法[9-10]的數(shù)學(xué)模型可表示為
(3)
式中:下標(biāo)m表示所選主基準(zhǔn)站的標(biāo)號;n表示副基準(zhǔn)站標(biāo)號,取值為(1,2,…,n),其中不包括主基準(zhǔn)站m,局域網(wǎng)中基準(zhǔn)站個數(shù)不少于3個,即n+m≥3;Δxnm和Δynm表示副基準(zhǔn)站n與主基準(zhǔn)站m的平面坐標(biāo)值之差;φ1和φ2分別表示Δx和Δy的系數(shù),即所求內(nèi)插系數(shù);vnm表示副基準(zhǔn)站n的偽距改正值與主基準(zhǔn)站m的偽距改正值之差,即副基準(zhǔn)站到主基準(zhǔn)站的距離改正誤差。
位于基準(zhǔn)站所構(gòu)成的多邊形網(wǎng)內(nèi)的流動站可以采用二維線性模型內(nèi)插出流動站到主基準(zhǔn)站的距離改正誤差,其用公式表示為
Vum=φ1·ΔXum+φ2·ΔYum。
(4)
式中:ΔXum和ΔYum表示流動站與主基準(zhǔn)站的平面坐標(biāo)差值;Vum表示流動站的偽距改正值與主基準(zhǔn)站偽距改正值之差,即流動站到主基準(zhǔn)站的距離改正誤差。
采用最小二乘間接平差法求定內(nèi)插系數(shù)φ1和φ2,過程中需要考慮不同基準(zhǔn)站與流動站間距離的遠(yuǎn)近,可以引入權(quán)陣P為

(5)
式中:pn為副基準(zhǔn)站n對流動站影響的權(quán)因子。定權(quán)公式為

(6)
式中:dun表示流動站到每個副基準(zhǔn)站的距離。
內(nèi)插系數(shù)φ1和φ2的求解公式可表示為
(7)
將系數(shù)φ1和φ2帶入式(4)求出流動站到主基準(zhǔn)站的距離改正誤差Vum,然后利用式(8)求得流動站最終偽距改正數(shù)Vu為
Vu=Vm+Vum。
(8)
式中:Vm為主基準(zhǔn)站的偽距改正數(shù)。
該模型中引入權(quán)陣,顧及了基準(zhǔn)站位置不同對偽距改正數(shù)影響程度的差異,用戶的定位精度較單站差分有明顯提高;但是當(dāng)用戶位于由基準(zhǔn)站所構(gòu)成的多邊形區(qū)域以外時效果則不太理想。由于該方法可以自主選擇主基準(zhǔn)站,因此使用起來較為靈活。
1.3 低次曲面模型法
主要介紹平面模型,其模型為
Vum=φ1·ΔXum+φ2·ΔYum+φ3。
(9)
式中各變量的含義與式(4)中的參數(shù)所表示含義相同,不同之處在于平面模型含有3個內(nèi)插系數(shù),因此平面模型至少需要4個基準(zhǔn)站;另外,線性內(nèi)插法是低次曲面模型法的一種特例[9-10],下面簡單介紹該方法。
采用最小二乘平差法內(nèi)插出系數(shù)φ1、φ2和φ3,公式為
(10)
將系數(shù)φ1、φ2和φ3帶入式(9)求出流動站到主基準(zhǔn)站的距離改正誤差Vum,利用式(8)求出流動站最終的偽距改正數(shù)Vu。
該模型考慮了基準(zhǔn)站位置的不同對偽距改正數(shù)影響程度的差異,同時也把隨機(jī)誤差考慮在內(nèi);但是對于低次曲面模型來說,局域網(wǎng)中基準(zhǔn)站的個數(shù)取決于低次曲面模型的變量個數(shù)和次數(shù):所以該方法對基準(zhǔn)站數(shù)量要求較高,最少需要4個基準(zhǔn)站。當(dāng)區(qū)域網(wǎng)內(nèi)基準(zhǔn)站分布均勻、數(shù)量充足時,該方法較為適合。
2 數(shù)據(jù)處理與分析
試驗數(shù)據(jù)來自中國測繪科學(xué)研究院在四川建立的BDS/GPS連續(xù)運行衛(wèi)星定位服務(wù)綜合系統(tǒng)(continuousoperationalreferencesystem,CORS)網(wǎng)。選取該CORS網(wǎng)中的MNYG、SUNG、RNXN、LESN、JNYG、PENZ和MNZU7個站構(gòu)成局域差分網(wǎng)基準(zhǔn)站,選取ZNZG這一CORS站作為網(wǎng)內(nèi)流動站,其中各CORS站的精確坐標(biāo)已知。根據(jù)基準(zhǔn)站和流動站的精確坐標(biāo)得到CORS站的空間位置分布圖,如圖1所示。
為尋找一個最適合網(wǎng)絡(luò)偽距差分方法的內(nèi)插方法,作者基于VisualStudioC++平臺分別編寫了基于反距離權(quán)重插值法、線性內(nèi)插法和低次曲面模型法生成流動站誤差改正數(shù)的多基站BDS/GPS融合偽距差分定位系統(tǒng)。方案①選取MNYG、SUNG、RNXN、LESN、JNYG、PENZ和MNZU7個CORS站構(gòu)成局域差分網(wǎng)基準(zhǔn)站;方案②選取MNYG、SUNG、RNXN、LESN、PENZ和MNZU6個CORS站構(gòu)成局域差分網(wǎng)基準(zhǔn)站;方案③選取MNYG、SUNG、JNYG、PENZ和MNZU5個CORS站構(gòu)成局域差分網(wǎng)基準(zhǔn)站;方案④選取MNYG、SUNG、JNYG和PENZ4個CORS站構(gòu)成局域差分網(wǎng)基準(zhǔn)站;方案⑤選取MNYG、SUNG和PENZ3個CORS站構(gòu)成局域差分網(wǎng)基準(zhǔn)站。分別利用3種內(nèi)插方法分別進(jìn)行BDS/GPS融合偽距差分定位解算,以尋找一個最適合網(wǎng)絡(luò)偽距差分方法的內(nèi)插方法。
試驗數(shù)據(jù)選取GPS時(GPStime,GPST)2015-07-27T00:00:00—23:59:59,采樣率為1s,衛(wèi)星截止高度角為10°,共24h的數(shù)據(jù)進(jìn)行BDS/GPS融合偽距差分定位解算,將各方案定位結(jié)果與流動站已知精確坐標(biāo)求差,如圖2至圖6所示為方案①至方案⑤北(N)、東(E)、天(U)方向分量殘差序列圖。由以上各方案通過BDS/GPS融合偽距差分定位后,對定位結(jié)果均方根誤差(rootmeansquare,RMS)進(jìn)行了統(tǒng)計,如表1所示。
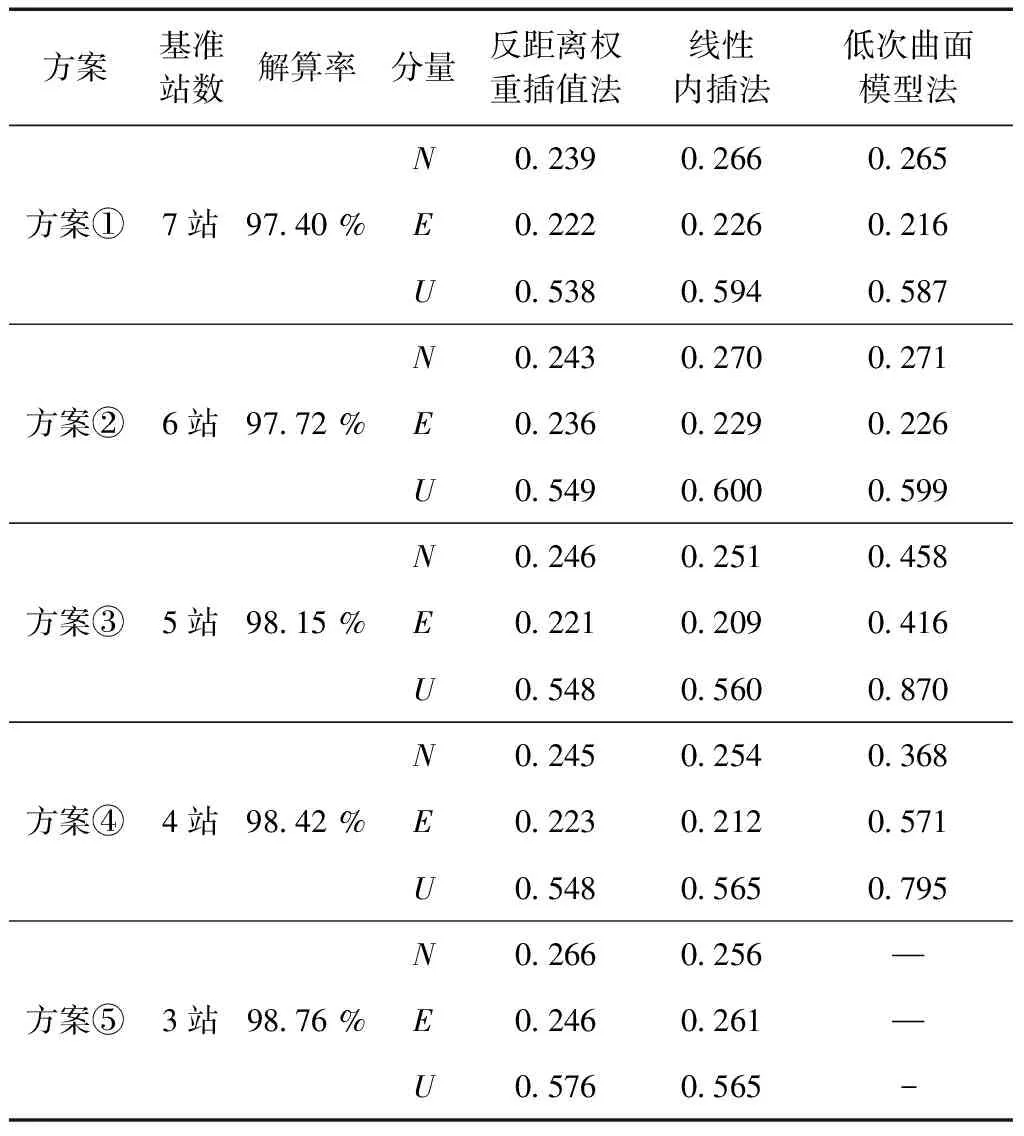
表1 各方案定位結(jié)果RMS統(tǒng)計表 m
通過圖2~圖3和表1對比可知,當(dāng)流動站在基準(zhǔn)站構(gòu)成的多邊形網(wǎng)內(nèi),且流動站附近可利用的基準(zhǔn)站數(shù)不少于6站時,利用反距離權(quán)重插值法、線性內(nèi)插法和低次曲面模型法生成偽距改正數(shù),進(jìn)行BDS/GPS融合偽距差分定位所獲得的定位精度相當(dāng),采用這3種方法都可以得到較高的定位精度。
通過圖4~圖5和表1對比可知,當(dāng)流動站在基準(zhǔn)站構(gòu)成的多邊形網(wǎng)內(nèi),且流動站附近可利用的基準(zhǔn)站數(shù)不少于4站并最多存在5站時,3種方法生成偽距改正數(shù),進(jìn)行BDS/GPS融合偽距差分定位,反距離權(quán)重插值法和線性內(nèi)插法獲得的定位精度相當(dāng),高于低次曲面模型法獲得的定位精度,采用反距離權(quán)重插值法和線性內(nèi)插法這2種方法可以得到較高的定位精度。
通過圖6和表1對比可知:當(dāng)流動站在基準(zhǔn)站構(gòu)成的多邊形網(wǎng)內(nèi),且流動站附近可利用的基準(zhǔn)站數(shù)只有3站時,無法利用低次曲面模型法生成偽距改正數(shù),另外2種方法生成偽距改正數(shù),進(jìn)行BDS/GPS融合偽距差分定位獲得的定位精度相當(dāng),采用反距離權(quán)重插值法和線性內(nèi)插法這2種方法可以得到較高的定位精度。
另外,根據(jù)表1的統(tǒng)計數(shù)據(jù)顯示:當(dāng)采用的基準(zhǔn)站數(shù)量逐漸減少時,3種方法的解算率逐漸提高;在BDS/GPS融合偽距差分定位精度方面,利用反距離權(quán)重插值法和線性內(nèi)插法生成偽距改正數(shù),所獲得的定位精度并不會因基準(zhǔn)站數(shù)量的減少而降低,而是趨于穩(wěn)定,相反,低次曲面模型法獲得的定位精度會相對降低。
3 結(jié)束語
從總體來看,當(dāng)用戶附近可利用的基準(zhǔn)站數(shù)不少于3站時,考慮BDS/GPS融合偽距差分定位的精度和解算率問題,采用離用戶較近的3個基準(zhǔn)站構(gòu)成多邊形網(wǎng)且用戶在多邊形網(wǎng)內(nèi),利用反距離權(quán)重插值法或線性內(nèi)插法生成偽距改正數(shù)進(jìn)行BDS/GPS融合偽距差分定位,所獲得的定位效率和精度更優(yōu)。
[1] 馬智偉.中國北斗衛(wèi)星導(dǎo)航產(chǎn)業(yè)整體發(fā)展現(xiàn)狀及趨勢:《2013-2014年中國北斗導(dǎo)航產(chǎn)業(yè)發(fā)展藍(lán)皮書》發(fā)布[J].衛(wèi)星應(yīng)用,2014(9):56-59.
[2] 李鶴峰,秘金鐘,黨亞民,等.基于CORS的多基準(zhǔn)站BDS/GPS融合差分網(wǎng)定位性能分析[J].大地測量與地球動力學(xué),2014,34(6):81-85.
[3] 2012年中國衛(wèi)星應(yīng)用若干重大進(jìn)展[J].衛(wèi)星應(yīng)用,2013(1):16-25.
[4] 徐忠燕,張傳定.局域差分GPS改正數(shù)學(xué)模型分析與比較[J].海洋測繪,2007,27(1):24-26.
[5] 高星偉,過靜珺,程鵬飛,等.基于時空系統(tǒng)統(tǒng)一的北斗與GPS融合定位[J].測繪學(xué)報,2012,41(5):743-748.
[6] 劉琳.BDS/GPS雙模差分定位技術(shù)的研究及實現(xiàn)[D].北京:北京交通大學(xué),2013:5-38.
[7] 李征航,黃勁松.GPS測量與數(shù)據(jù)處理[M].武漢:武漢大學(xué)出版社,2010:173-180.
[8] DALE Z, CLAIRE P, AMY R, et al.An experimental comparison of ordinary and universal Kriging and inverse distance weight[J].Mathematical Geology,1999,31(4):375-390.
[9] DAI L, HAN S, WANG J, et al.Comparison of interpolation algorithms in network-based GPS techniques[J]. Navigation,2002,50(4):277-293.
[10]徐周.GPS差分定位技術(shù)及實現(xiàn)方法的研究[D].鄭州:信息工程大學(xué),2006:32-34.
Comparisonbetween three interpolation methods of BDS/GPS pseudo-range differential correction
ZHOUWanzhen1,2,BEIJinzhong2,LIDehai2,FANGShushan2,CHENZhen3,YUMengyang1,2
(1.Geomatics College, Shandong University of Science and Technology, Qingdao, Shandong 266590, China;2.Chinese Academy of Surveying and Mapping, Beijing 100830, China;3.Research Institute of Qingdao Surveying and Mapping, Qingdao, Shandong 2660000, China)
Aiming at the problem that the efficiency of each interpolation method that uses the correction of reference stations to generate the user pseudo-range correction is usually influenced by the distance between the user and the reference stations, and the number of reference stations in the BDS/GPS fusion pseudo-range differential positioning, the paper analyzed the the accuracy and efficiency of inverse distance weighted interpolation method, linear interpolation method and low-order surface model under different numbers of reference stations in BDS/GPS fusion pseudo-range differential positioning, and proposed the optimal interpolation method for BDS/GPS fusion pseudo-range differential positioning.Experimental result showed that the efficiency and accuracy of BDS/GPS fusion pseudo-range differential positioning would be optimal by using the inverse distance weighted interpolation method or linear interpolation method to generate the pseudo-range correction, when the number of available reference stations near the user is not less than three and a polygon mesh could be formed with three nearer reference stations to make the user within the mesh.
BDS/GPS fusion pseudo-range differential positioning; inverse distance weighted interpolation method; linear interpolation method; low-order surface model
2016-08-12
國家自然科學(xué)基金項目(41304030);科技部863計劃項目(2015AA124001);國家重點研發(fā)計劃項目(2016YFB0502105,2016YFB0501801);北斗分析中心資助項目(GFZX0301040308-06);中國測繪科學(xué)研究院基本科研業(yè)務(wù)費項目(7771604)。
周萬振(1991—),男,山東濟(jì)南人,碩士研究生,研究方向為GNSS差分定位技術(shù)。
秘金鐘(1975—),男,河北衡水人,博士,研究員,研究方向為大地測量與GNSS衛(wèi)星導(dǎo)航。
周萬振,秘金鐘,李得海,等.BDS/GPS偽距差分改正數(shù)3種內(nèi)插方法的比較[J].導(dǎo)航定位學(xué)報,2017,5(2):79-85.(ZHOU Wanzhen, BEI Jinzhong, LI Dehai,et al.Comparison between three interpolation methods of BDS/GPS pseudo-range differential correction[J].Journal of Navigation and Positioning,2017,5(2):79-85.)
10.16547/j.cnki.10-1096.20170214.
P228
A
2095-4999(2017)02-0079-07

