立體幾何與向量的理性分析

黃茂源

湖南師范大學附屬中學

【摘要】立體幾何與向量這一知識點學生在學習中存在問題和難度。對立體幾何與向量學習弊端和主要根源進行分析和研究，發(fā)現(xiàn)主要是對理論概念理解錯誤和對空間理論理解錯誤導致。面對這一現(xiàn)象，需要開展對立體幾何與向量的理性分析和研究，加強對立體幾何與向量學習方法和技巧的了解，提高學習能力。

【關鍵詞】立體幾何；向量；理性分析

高中立體幾何與向量的學習中，應重點掌握知識關鍵點，例如向量大小能夠使用平行四邊形理論闡述。學生結合向量大小不同，進行類型劃分，保證解題的準確性。立體幾何的選擇形式也是數(shù)學解題的重點。一旦理解偏差，會造成解題的方向性錯誤，最后得出錯誤答案。由此，在立體幾何與向量的理性分析中，應重點掌握課堂學習中存在的弊端，加以有效避免，保證數(shù)學解題思路的正確性，下面進行詳細闡述。

一、立體幾何與向量學習弊端

為了提高對立體幾何與向量學習的關注度和認識度，教師首先要對學習情況進行理性分析和研究，發(fā)現(xiàn)學生學習弊端，并加以改進。

其一，學生對理論和概念理解不深刻，導致其對概念的理解淺顯。比如容易忽略向量確立條件；在實際解題中忘記向量平行這一理論；把點與平面之間的距離理解為點到其平面中一個點的距離；誤認為二角理論是在平面圖形中；垂直和相交的線段產生角度知識混淆；對向量和數(shù)積理論理解錯誤；等等。

其二，對空間概念理解錯誤。這一問題在高中生中普遍存在。例如已知向量a的集合為（-1，3，3），向量b的集合為（2，7，-4），問題是解出ab集合和ab向量的積。其實這一集合向量習題對高中生來說不是一個難點問題，但是理論性理解失誤則會導致出現(xiàn)計算失誤。因此，對于a、b這兩個向量和，直接利用ab向量子集來進行相加運算，得出ab向量的子集和為12；對于ab向量的積則認為是a向量和b向量的乘積，得出其數(shù)值為（-2，35，-12）。由此可見，學生在實際解題和學習過程中容易伴有理論理解錯誤弊端，導致向量加法和乘法計算存在錯誤。這一問題和弊端的產生，主要是由于把向量的加法和乘法定義理解混淆導致的，沒有認清這兩個不同的向量定義，忽略其具有共同性的向量。

其三，線段和向量的認知錯誤也是當下向量學習的重點。例如AB線段和CD線段相等，AB向量和CD向量相等，學生在實際學習和解題中會誤認為這兩個不同夾角和異面產生的夾角具有相同性，誤認為直線和向量的關系具有平行性。又如a線段和b線段具有平行關系，b線段和c線段具有平行關系，學生則依據(jù)這一關系特點，認為向量a和向量c具有平行關系，向量a和向量b具有平行關系，那么向量b和向量c也具有平行關系。面對這一情況，學生要加強對自身薄弱環(huán)節(jié)的學習。

二、立體幾何與向量的理性分析

立體幾何與向量的知識具有聯(lián)系。就向量來說，其理論要點可以闡述為幾個具有方向的量，可以用數(shù)字大小來表示。對于向量的表示，主要是利用線段表示量的大小，利用模分析向量的大小。在對已知向量對向量大小進行判斷和分析中，利用數(shù)學方程形式表達則是把a思維模表現(xiàn)為{a}。零向量的模記作0的向量模，直接用0表示即可。單一就0向量來說，其不具有固定方向。因此，0向量在立體幾何題中應用，可以和不同向量共線。相同性和等量性向量，方向具有相同性，這是我們利用向量解題時需要注意的點。

（一）立體幾何與向量的應用

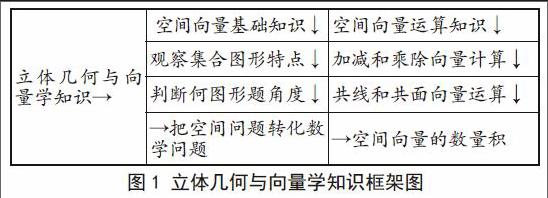
在立體幾何解題和學習中應用向量，首先可以利用圖形構建一個向量和圖形結合的理論思維，具有較好的實際應用性，避免了傳統(tǒng)學習和解題的弊端。站在實際運用角度來說，我們利用這一方法進行解題和學習，首先，要加強對空間概念的了解，依據(jù)集合圖形和向量的特點，構建一個具有向量的幾何圖形，構建集合解題模型。我們要站在不同角度觀察這一集合圖形特點，結合數(shù)形結合方法，分析和判斷出其是鈍角幾何圖形還是銳角集合圖形，分析其相等角和補角度數(shù)，把空間問題轉化為數(shù)學問題。其次，為了保證立體幾何與向量學習有效性，我們在學習和解題時，可以構建一個立體幾何與向量學知識框架圖進行學習。如圖1所示，是立體幾何與向量學知識框架圖。

（二）加法和減法向量在立體幾何中的應用分析

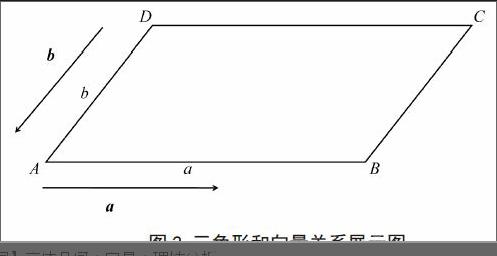
對于加法向量和減法向量在立體幾何中的應用，本文主要是講在三角形這一集合圖形中的應用。圖2是三角形和向量關系展示圖。在結合圖形基礎上，計算出這一三角幾何圖形的向量和。在對三角形和向量關系分析和研究后，增加對向量和三角形判斷。在三角形中隨意取一個點，用字母A表示，結合圖形設置AB長度和a向量長度具有相等性，AD長度和b向量長度相等，則可以把AC稱為a，b這兩個向量的和，也可以稱AC是和向量。利用數(shù)學公式的形式，則可以把其展現(xiàn)為a+b，也可以說a，b相加等于AB和BC相加的和，也就是等于AC。因此，我們可以說a，b相加與AB和BC相加、AC具有相等性。

三、結束語

由上文我們可以看出，立體幾何與向量具有緊密聯(lián)系，可以解決我們在實際學習和解題中的難題，具有較好的實際應用性。但是需要注意的是，我們在立體幾何與向量學習和解題中存在問題，要加以改正和完善，加強理論知識學習，提高對空間向量特點的認知度，提高空間圖形布局和設置的能力，樹立科學的解題和學習理念。

【參考文獻】

[1]杜瑞姣.高中立體幾何高考試題分析及教學對策研究[D].洛陽：洛陽師范學院，2016.

[2]高愛環(huán).高中生用向量法解決立體幾何問題的調查研究[D].石家莊：河北師范大學，2016.

[3]陸文鳳.立體幾何教學研究[D].呼和浩特：內蒙古師范大學，2013.