基于B樣條的凸輪式開關機構輪廓線設計方法

王 偉 姚華忠

福州大學機械工程及自動化學院，福州，350116

基于B樣條的凸輪式開關機構輪廓線設計方法

王 偉 姚華忠

福州大學機械工程及自動化學院，福州，350116

針對凸輪式開關機構輪廓線與力值曲線定量關系復雜、輪廓線形狀描述困難的問題，采用B樣條方法，依據能量理論研究了開關機構輪廓線的設計方法。給出了開關機構B樣條曲線描述方程及其微分表達式，建立了機構內部彈性勢能與外力功的關系式，提出了輪廓線逐步迭代設計算法。利用MATLAB設計了雨刷開關機構輪廓線，結果表明根據能量關系設計開關機構輪廓曲線能達到預期的力值要求,采用B樣條曲線方程比高次多項式擬合方程更能有效提高輪廓線設計精度和開關設計質量。

凸輪式開關；輪廓線；能量關系；B樣條

0 引言

凸輪式開關在汽車領域得到廣泛應用，如汽車的雨刷開關、空調開關、轉向燈開關等。手感是凸輪式開關的重要性能指標，該指標由開關的行程感、力感、擋位感等力特性反映，汽車主機廠用開關的力值曲線來描述開關的力特性指標，并將其作為開關設計規范要求[1-2]。當開關的材質確定后，開關的力值曲線就由開關輪廓線決定,因此，輪廓線的設計是凸輪式開關設計的關鍵，研究凸輪式開關機構輪廓線設計方法具有重要意義。

凸輪輪廓線設計是典型的反求設計問題。張金萍等[3]采用反求工程技術，研究了實測凸輪廓線數據的曲線重構問題，反求設計了高速凸輪廓線。侯悅民等[4]研究了凸輪運動特性的反求設計問題，用樣條方法對從動件常用運動規律進行逼近和優化，改善了凸輪運動特性。

凸輪式開關輪廓線設計是基于力特性的反求設計問題，它要求設計出來的凸輪廓線要在運動周期內具有預期的驅動力矩規律。ERDELYI等[5]針對凸輪廓線力特性反求設計問題，建立了開關輪廓線與手柄驅動力的關系模型，用離散點描述輪廓線，用差分方法分析輪廓線幾何關系，設計了汽車轉向開關結構輪廓線。

凸輪式開關機構輪廓線是一種復雜型線，需要一種高精度的輪廓線描述方法。B樣條曲線具有逼近程度高、適應性強、計算簡便且便于控制等優點，在凸輪廓線設計中得到廣泛應用[6]。TSAY等[7]應用B樣條曲線研究了多約束凸輪廓線反求設計問題，實現了運動特性的改善。MANDAL等[8]研究了凸輪B樣條曲線控制點反求的優化方法，改善了從動件加速度特性。毛征宇等[9]采用B樣條方法對復雜曲線進行擬合，并綜合誤差、速度和加速度等因素，給出具有自適應調整能力的插補步長確定算法，實驗證明采用B樣條插補可以保證復雜曲線插補加工的高速與高精度，且具有很好的速度、加速度以及加加速度平滑性。

三次B樣條凸輪廓線具有二階連續特性，合理確定廓線能獲得較好的凸輪性能，故在改善凸輪高速運動性能上得到廣泛應用[10]。凸輪式開關雖然轉速不高，但要求整個擋位周期處處滿足力值要求，這需要高精度的廓線方程，因為只有高精度的廓線方程才能建立準確的開關受力關系和能量關系，進而實現力值要求的精確滿足。ERDELYI 等[5]采用離散點的差分方程描述廓線,但精度不夠高。本文利用三次均勻B樣條曲線來描述凸輪式開關復雜輪廓線，建立凸輪廓線與力值的定量關系，實現凸輪廓線的設計。

1 開關結構及輪廓線B樣條曲線方程

1.1 凸輪式開關結構

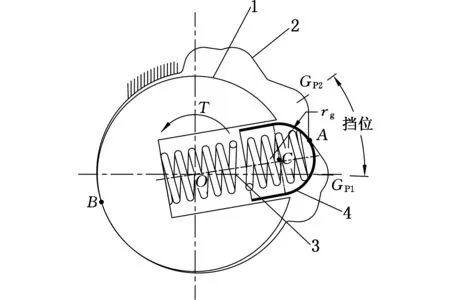
(a)機構原理圖

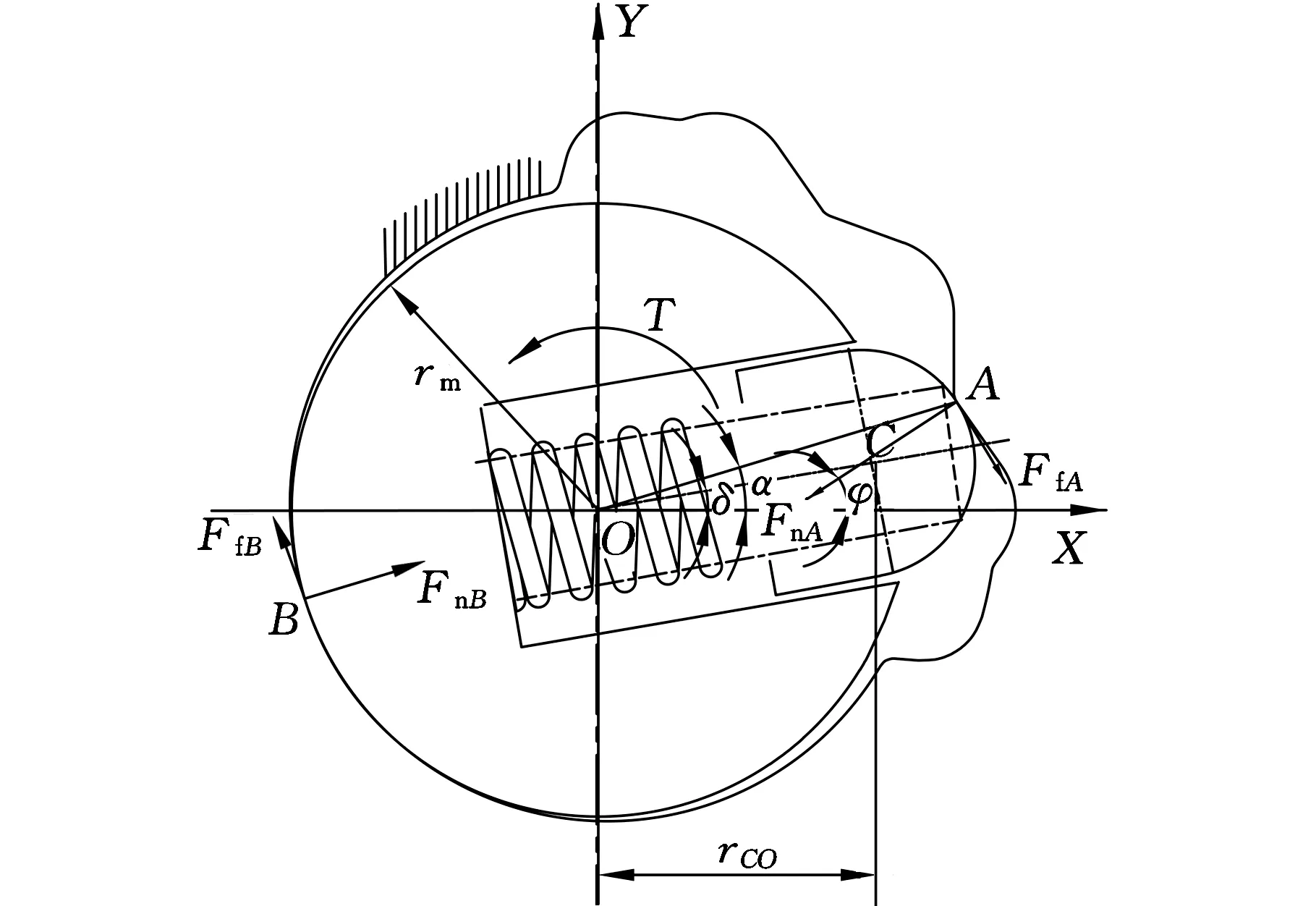
(b)受力分析圖1.開關軸 2.凸輪廓線 3.彈簧 4.擋銷圖1 凸輪式開關結構Fig.1 Structural of cam-type switching mechanism

凸輪式開關機構如圖1所示，軸1的徑向圓孔裝有壓縮彈簧3，擋銷4由薄壁圓筒和薄壁半圓球組成，薄壁圓筒段起導向作用，擋銷半圓球面靠壓簧與固定的凸輪廓線2接觸，并隨軸的轉動而沿輪廓線表面滑動。開關根據需要由一到多個擋位組成，圖中凸輪廓線的GP1GP2段是開關一個擋位的典型結構，經歷波谷-波峰-波谷循環，輪廓線需要滿足對應擋位的預期力值要求。

1.2 輪廓線的三次B樣條曲線方程

圖1b開關力模型中，凸輪理論廓線為擋銷圓心(滾子中心)的運動軌跡。擋銷圓心軌跡是一條自由曲線，由三次B樣條曲線逼近，要求樣條曲線通過擋銷圓心位置點PCi(i=0,1,…，n-1)。該曲線由n-1段B樣條曲線組成，B樣條曲線方程為

QCi(t)=

(1)

式中,QCi(t)為擋銷圓心樣條曲線第i段，i=0,1,…,n-2；t為參數，0≤t≤1 ；VCi為樣條曲線控制點，i=0,1,…,n+1。

B樣條曲線一階導數為

(2)

B樣條曲線方程滿足：

(1)連續性條件

QC(i-1)(1)=QCi(0)=PCii=1,2,…,n-2

(2)首末端點條件

QC0(0)=PC0QC(n-2)(1)=PC(n-1)
VC0(0)=VC1VC(n+1)=VC(n)

由以上條件和式(1)可得

(3)

求解式(3)可得到控制點VCi(i=0,1,…,n+1)，再將控制點代入式(1)即得到樣條曲線方程。

凸輪實際廓線為接觸點A的軌跡，其極半徑為

(4)

式中,rg為擋銷半徑;rc為擋銷中心位置的極半徑。

2 開關機構力學模型

凸輪式開關在工作過程中，擋銷隨凸輪軸的轉動在凸輪上滑動，依靠凸輪軸輸入的手柄力矩克服摩擦功和阻尼功，同時彈簧存儲彈性勢能。由于開關速度低以及擋銷質量小，故忽略系統的動能和阻尼功,開關機構系統能量關系方程為

W=ΔEp

(5)

式中，W為系統外力功,W=WT-Wf1-Wf2；ΔEp為彈簧彈性勢能改變量；WT、Wf1、Wf2分別為凸輪軸力矩輸入功、擋銷摩擦功、凸輪軸摩擦功。

給定凸輪軸扭矩T、凸輪預壓縮量為S0、凸輪軸轉角δ時的彈簧壓縮量S(δ)，則凸輪軸力矩輸入功、勢能改變量、摩擦功分別為

(6)

FnB=kS

式中,F為彈簧力；FnA為擋銷接觸點正壓力；FnB為軸與凸輪接觸點正壓力；k、μ1、μ2分別為彈簧彈性系數、軸-凸輪副摩擦因數、擋銷-凸輪副摩擦因數；rm為凸輪軸半徑。

3 開關機構輪廓線設計算法

由于機構外力功和彈性勢能都與彈簧壓縮量S(δ)有關，機構的能量關系方程為彈簧壓縮量的隱式方程，因此開關機構輪廓線設計需要通過迭代求解彈簧壓縮量，進而確定開關機構理論和實際廓線。具體步驟如下：

(1)不考慮摩擦功，將計算得到的彈簧壓縮量作為迭代計算的初始值。在式(5)中令摩擦功為零，得到彈簧壓縮量迭代計算的初值

(7)

(2)考慮摩擦功，求解彈簧壓縮量:

(8)

判別彈簧壓縮量計算是否收斂。如果不收斂，按迭代公式計算彈簧壓縮量的迭代值和新的輪廓線，并返回到步驟(2)進行下一輪迭代；如果收斂，進入步驟(3)。迭代公式為

S(g)(δ)=S(g-1)(δ)+ξ(Snew(δ)-S(g-1)(δ))

(9)

式中，ξ為松弛系數，0<ξ<1。

(3)確定凸輪理論廓線和實際廓線。理論廓線為擋銷中心軌跡，其直角坐標為

(10)

式中，rCO為擋銷中心初始位置處的極半徑。

實際廓線坐標方程為

(11)

(4)力值曲線校核。根據所獲得的輪廓線，計算凸輪驅動力矩，并將其與預期的力值曲線進行比較。凸輪升程段驅動力矩方程為

T=FnArAsin(φ-δ-θ)+μ2FnArAcos(φ-δ-θ)+
μ1FnBrm

(12)

凸輪回程段驅動力矩方程為

T=-FnArAsin(φ-δ+θ)-μ2FnArAcos(φ-δ+θ)+
μ1FnBrm

(13)

計算流程如圖2所示。

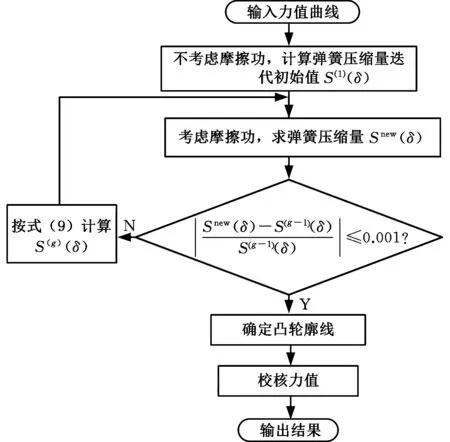
圖2 凸輪式開關輪廓線設計流程圖Fig.2 Flowchart of cam-type switch contour design

4 開關機構輪廓線設計算例及結果討論

4.1 開關機構凸輪廓線反求設計算例

某凸輪式雨刷開關期望力值曲線如圖3所示，開關的結構與物理參數如表1所示。

圖3 雨刷開關期望力值曲線Fig.3 Expected force value curve of the wiper switch

表1 雨刷開關結構與物理參數表Tab.1 The structural and physical parameters of wiper switch

圖3中P點和C點分別對應力值峰值點和谷值點，Z點對應擋位結束位置。峰值行程感指標用峰值點行程δP與總行程δZ的比值(δP/δZ)描述，該指標反映開關轉動力矩達到峰值的快慢；擋位感指標用人手感覺到的落差力矩與對應行程的比值(TP-TC)/δC來描述。在雨刷開關中峰值行程感指標和擋位感指標分別為0.1857 N·mm/(°)、0.3814 N·mm/(°)。

利用MATLAB語言對本文輪廓線設計方法進行編程，計算得到雨刷開關輪廓線，彈簧壓縮量迭代計算過程以及雨刷開關理論輪廓線和實際輪廓線如圖4所示。

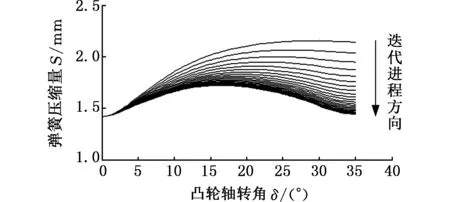
(a)彈簧壓縮量曲線迭代過程

(b)雨刷開關輪廓線圖圖4 彈簧壓縮量迭代計算及輪廓線設計結果Fig.4 Iterative computation of the spring compression value and the design results of the switch contour curve

圖5所示為期望力值曲線與設計力值曲線。設計力值曲線包括按三次均勻B樣條輪廓曲線和按五次多項式曲線獲得的力值結果。

圖5 期望力值曲線與設計力值曲線Fig.5 The comparison of the expected force value curve and the designed force value curve

4.2 設計結果討論

(1)從圖4可以看出，隨著迭代過程的進行，彈簧壓縮量曲線逐漸收斂，并且終了位置的彈簧壓縮量和初始位置彈簧壓縮量相等，實現擋位復位。這表明采用能量法進行凸輪式開關力值特性的輪廓線反求設計是可行的。

(2)從圖5可以看出，采用B樣條所獲得的力值曲線較五次多項式輪廓線的力值曲線更接近期望力值曲線，其中B樣條的力值曲線與期望力值曲線相關系數為0.996，五次多項式輪廓線的力值曲線與期望力值曲線的相關系數為0.986；在擋位初始和末了兩個階段，五次多項式輪廓線的力值曲線與期望力值曲線有較大的誤差，而采用B樣條所求力值曲線與期望的力值曲線基本一致。這表明，B樣條曲線設計能夠提高輪廓線的設計精度和開關的使用性能。

(3)B樣條輪廓線得到的力值曲線在擋位推程和擋位回程末了兩個階段與期望力值曲線誤差很小，而在回程的中段誤差相對大些，可能是因擋銷在這一工作段用庫侖摩擦模型與實際接觸的摩擦規律有誤差導致。由此，這一段凸輪廓線的摩擦規律以及對凸輪廓線設計的影響有待進一步研究。

5 結論

(1)提出了一種根據力值特性進行開關凸輪廓線反求設計的方法，給出了凸輪機構能量關系方程、三次均勻B樣條凸輪廓線方程以及數值迭代算法。

(2)雨刷開關設計實例表明，本文提出的采用能量法進行凸輪廓線反求設計是可行的，可以普遍適用于根據力值特性進行凸輪廓線的反求設計。

(3)B樣條曲線適合于凸輪式開關復雜輪廓型線的設計，能夠有效提高設計精度和開關的使用性能。

[1] 劉克軍,范學,李高林. 開關力特性曲線研究[J]. 汽車電器,2012,51(7):9-11.LIUKejun,FANXue,LIGaolin.OnthePerformanceCurveofSwitchPower[J].AutoElectricParts，2012,51(7):9-11.

[2] 劉巖睿，夏群生，何樂. 汽車轉向管柱組合開關的力特性研究[J]. 汽車工程,2003,26(3):336-340.LIUYanrui，XIAQunsheng，HELe.TestandMeasurementofMechanicalCharacteristicofMulti-FunctionSwitchSystemonVehicles[J].AutomotiveEngineering，2003,26(3):336-340.

[3] 張金萍，羅鵬，張利國，等. 基于等距三次均勻有理B樣條曲線反求設計方法的研究[J]. 沈陽化工學院學報,2005,19(3):216-219.ZHANGJinping,LUOPeng,ZHANGLiguo,etal.ReverseDesignofHighPrecisionCamBasedonOffsetCubicUniformRationalB-splineCurve[J].JournalofShenyangInstituteofChemicalTechnology,2005,19(3):216-219.

[4] 侯悅民，張偉，鮑莉. 利用三次均勻B樣條曲線優化設計凸輪廓線[J].農業機械學報,2003, 31(1):71-74.HOUYuemin,ZHANGWei,BAOLi.OptimizationofCamContourbyB-splineCurve[J].TransactionsoftheChineseSocietyofAgriculturalMachinery,2003,31(1):71-74.

[5]ERDELYIH,TALABAD.ANovelMethodfortheDynamicSynthesisofCamMechanismswithanImposedDrivingForceProfile[J].ProceedingsoftheInstitutionofMechanicalEngineers,PartC:JournalofMechanicalEngineeringScience,2010,224(8):1771-1782.

[6] 張永曙，劉克軒，蔣大為. 計算機輔助幾何設計的數學方法[M]. 西安:西北工業大學出版社,1986：166-167.ZHANGYongshu,LIUKexuan,JIANGDawei.MathematicalMethodsinComputerAidedGeometricDesign[M].Xi’an:NorthwesternPolytechnicalUniversityPress,1986：166-167.

[7]TSAYD,HUEYC.CamMotionSynthesisUsingSplineFunctions[J].JournalofMechanicalDesign,1988，110(2):161-165.

[8]MANDALM,NASKART.IntroductionofControlPointsinSplinesforSynthesisofOptimizedCamMotionProgram[J].MechanismandMachineTheory,2009,44(1):255-271.

[9] 毛征宇，劉中堅．一種三次均勻B樣條曲線的軌跡規劃方法[J]. 中國機械工程,2010，21(21)：2569-2572.MAOZhengyu,LIUZhongjian．ATrajectoryPlanningMethodforCubicUniformB-splineCurve[J].ChinaMechanicalEngineering,2010，21(21):2569-2572.

[10]TSAYDM,LINBJ.ImprovingtheGeometryDesignofCylindricalCamsUsingNonparametricRationalB-splines[J].Computer-AidedDesign,1996,28(1):5-15.

(編輯 袁興玲)

Design Method of Cam-type Switching Mechanism Contours Based on B-Spline

WANG Wei YAO Huazhong

College of Mechanical Engineering and Automation, Fuzhou University, Fuzhou, 350116

In order to investigate the problems of complex contour description and complex quantitative relationship between cam-type switching mechanism contours and force value curves, a design method of cam contour was suggested based on B-spline and energy theory. The descriptive and the differential equations of B-spline were given, the quantitative relationship equation between the internal potential energy and external work of switching mechanism was established, and the iterative design algorithm of mechanism contours was presented. A cam-type wiper switch contour was designed by using MATLAB and the suggested cam contour design method, which involved the energetic relationship equation and the iterative algorithm. The design results indicate that the derived contour may satisfy the expected force value curve requirements, and the derived force value curves by using B-spline are more effective in improving the contour precision and the switch performance than that by using high-order polynomial fitting curves.

cam-type switching mechanism；contour； energetic relationship； B-spline

2016-05-17

福建省工業機器人基礎部件技術重大研發平臺資助項目(2014H21010011)

TH112

10.3969/j.issn.1004-132X.2017.07.006

王 偉，男，1970年生。福州大學機械工程及自動化學院教授。主要研究方向為現代機械設計理論及方法、冶金設備及承壓設備力學。發表論文20余篇。E-mail：mkwang@fzu.edu.cn。姚華忠，男，1990年生。福州大學機械工程及自動化學院碩士研究生。