凸環管件顆粒介質內高壓成形工藝理論解析
楊卓云 趙長財 董國疆 張 鑫 陳曉華
1.燕山大學先進鍛壓成形技術與科學教育部重點實驗室,秦皇島,0660042.燕山大學車輛與能源學院,秦皇島,066004
凸環管件顆粒介質內高壓成形工藝理論解析
楊卓云1趙長財1董國疆2張 鑫1陳曉華1
1.燕山大學先進鍛壓成形技術與科學教育部重點實驗室,秦皇島,0660042.燕山大學車輛與能源學院,秦皇島,066004
離散體顆粒介質使顆粒介質內高壓成形工藝中的傳壓具有非均勻性、顆粒介質與管件之間摩擦作用顯著等特征,基于此,建立了顆粒介質非均勻載荷傳壓模型,對凸環管件脹形工藝過程進行了理論推導和數值解析,探討了內壓狀況和摩擦條件對管件成形性能的影響,并通過工藝試驗對理論分析結果進行了驗證。分析結果表明,顆粒介質內高壓成形工藝所具有的內壓非均勻性、介質與管坯摩擦作用顯著兩大特征可有效減小脹形過程中的壁厚減薄和成形壓力。對比試驗與理論分析結果表明,壁厚分布和成形壓力的理論計算結果與試驗結果一致,顆粒介質非均勻載荷傳壓模型的構建策略可用于管件成形的預測和分析。
顆粒介質;內高壓成形;管材;脹形
0 引言
內高壓成形技術是當前最為先進的變截面、空心薄壁管件的柔性加工方法,應用最廣泛的是以液體為傳力介質的液壓脹形工藝。管材脹形理論方面的研究大都是基于液壓脹形工藝開展的。管材液壓脹形所具有的特點是:內壓均勻分布,介質與管坯之間沒有摩擦且管端需特殊密封。在理論分析中,需要密封的管端一般給定為自由、封閉、固定和被動4種假設;自由脹形區管壁輪廓使用圓函數[1]或橢圓函數模型[2]。HE等[2-3]在脹形試驗理論分析中,應用了封閉管端、固定管端模型,以及與模具相關的橢圓輪廓假設,研究表明兩種管端條件下得到的管材應力應變曲線是一致的;與模具相關的橢圓輪廓假設比與模具無關的橢圓輪廓假設描述更加準確。HWANG等[4]關于管材脹形試驗和單向拉伸試驗的研究表明,考慮各向異性條件下得到的應力應變計算曲線與試驗結果更加接近。
顆粒介質內高壓成形工藝的特征在于:顆粒介質屬于摩擦型材料,內壓傳遞非均勻分布;顆粒介質與管材之間存在強烈的摩擦作用。這些特征使顆粒介質管材脹形理論分析與液壓脹形有顯著的差別。多年來本課題組一直致力于顆粒介質內高壓成形工藝的研究,在顆粒介質材料性能和成形工藝方面開展了大量的試驗和研究工作:對于顆粒介質的數值模擬模型方面提出了離散元與有限元分體耦合仿真分析的方法;在工藝試驗方面成功試制了不銹鋼、AZ31、AA7075、AA6061等材質的典型管、板材薄殼構件,并將此工藝推廣至軍工和航天領域[5-9]。郎利輝等[10]利用高溫顆粒介質對TA1鈦合金筒形零件的成形進行了有益的嘗試。陳國亮[11]采用陶瓷顆粒作為介質,對軟凹模和軟凸模兩種工藝進行了研究,分析了顆粒粒徑大小和填裝體積對成形性能的影響。袁海環[12]提出固體顆粒介質輔助板料拉深成形方法,研究表明顆粒介質的摩擦作用能夠有效抑制變形板坯的減薄。GRüNER等[13-14]以顆粒狀材料作為傳壓介質對板材進行拉深成形,在介質性能和工藝仿真方面開展了卓而有效的工作。諸多學者的研究表明,該工藝具有模具設計簡單、工藝實現簡便、方便應用于輕合金材料熱成形技術領域等特點。
本文以固體顆粒為傳壓介質,將壓頭施加的軸向壓力轉化為側向壓力使管材發生塑性變形。以自由脹形凸環管件為目標,在顆粒介質傳壓性能試驗的基礎上,建立管材顆粒介質自由脹形力學分析模型,分析管材在顆粒介質非均布內壓和摩擦共同作用下的變形機理,探討主要工藝參數對管件成形性能的影響。
1 材料性能試驗
1.1 顆粒介質性能
顆粒簇是由大量離散的固體顆粒相互作用而組成的復雜體系。顆粒之間的接觸非常復雜,導致顆粒介質的傳壓性能和外摩擦性能與眾不同。本文選用8號NMG(non-metallic granules),主要成分為ZrO2(質量分數為68%)和SiO2(質量分數為32%),洛氏硬度達到48~55HRC,粒徑在0.221~0.318 mm之間,屬于非黏性材料。當受到外載荷的擠壓作用時,顆粒間的接觸力(包括法向力和切向力)表現出很強的隨機性和復雜性,其力學行為難以用一般的固體力學和流體力學理論進行準確描述。本文通過顆粒介質傳壓性能試驗(圖1),尋找某些特定條件下的軸向壓力和徑向壓力的關系,以期為管材脹形工藝分析提供一個簡便可行的傳壓模型。試驗表明,壓頭壓力pN通過顆粒介質轉化為徑向壓力pR時,隨著測試點與壓頭距離的增大,徑向壓力逐漸減小。在不同壓頭力的作用下,徑向壓力的變化規律如圖2所示。根據試驗結果,徑向壓力的分布規律可用下式擬合:
pR=aebx
(1)
式中,x為測試點與壓頭距離,mm;a為徑向壓力系數,MPa,其取值與壓頭力相關;b為徑向壓力指數,mm-1,其取值與料筒直徑相關。
不同條件下的擬合值見表1。

圖1 顆粒介質傳壓性能試驗原理圖Fig.1 Experiment for pressure transmitting performance of granule medium
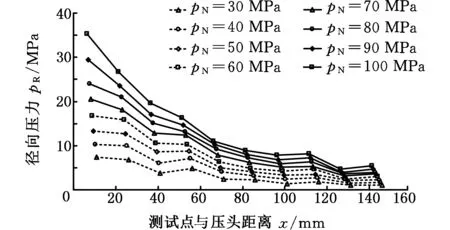
(a)料筒直徑100 mm

(b)料筒直徑80 mm
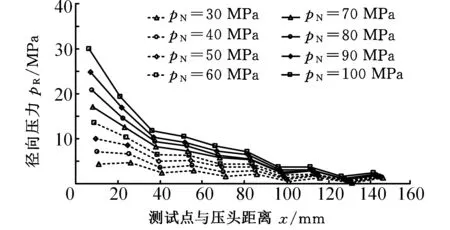
(c)料筒直徑60 mm圖2 徑向壓力pR分布曲線Fig.2 Curves of radial pressure pR
由與工藝試驗相同料筒直徑(100 mm)下的參數擬合值可知:b的變化與壓頭力不相關,取平均值為-0.014 56;a與壓頭力之間成線性變化規律,可用下式擬合:
a=0.3386pN
(2)
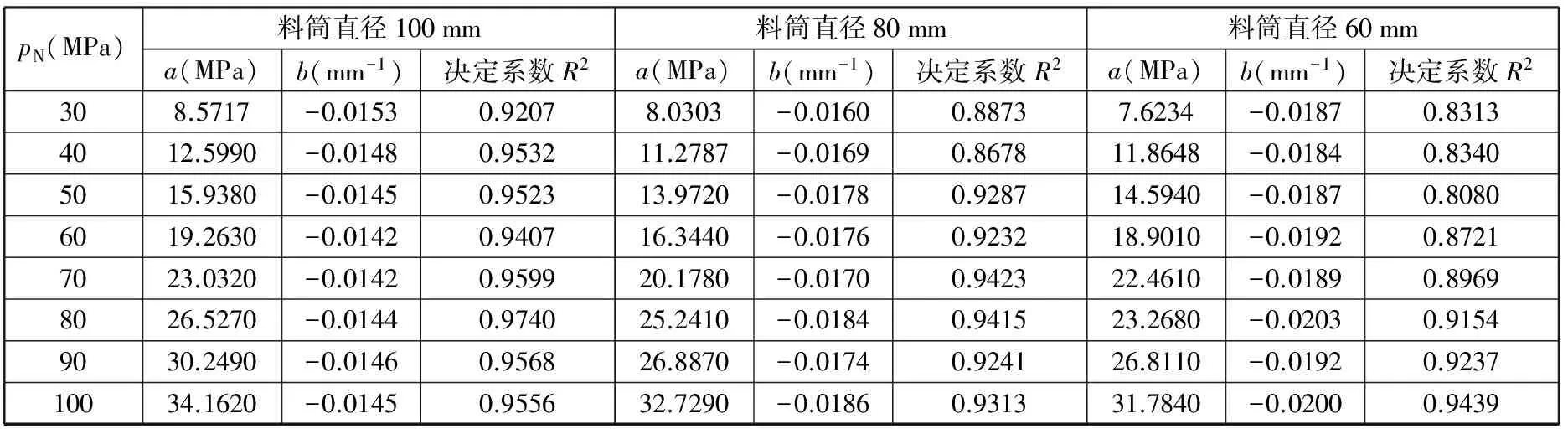
表1 徑向壓力公式相關參數擬合值
將式(2)代入式(1),可得到徑向壓力的分布公式:
pR=0.3386pNe-0.014 56x
(3)
文獻[7]通過顆粒介質摩擦強度測試得到了三種型號NMG外摩擦因數fw的變化規律(表2)。在管坯成形過程中,顆粒介質的徑向壓力不會超過75 MPa,因此8號NMG與管坯的摩擦因數μ1滿足以下公式:
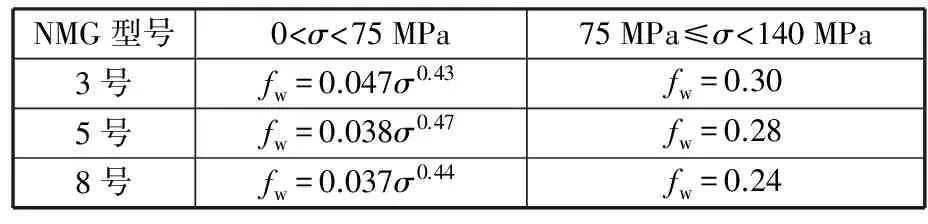
(4)
顆粒介質在受外載荷作用時,顆粒間的空隙會減小,表現為排列結構趨于緊密,顆粒介質產生體積減縮現象;同時,承載后顆粒體自身產生彈性變形,但這對顆粒介質體積減縮的貢獻微小。定義承載后顆粒介質體積減少量與承載前體積的比值為體積壓縮率η,試驗測定體積壓縮率的變化曲線見圖3。顆粒介質的體積壓縮率η隨壓頭壓力的變化規律可用線性方程進行擬合:
η=0.0007pN
(5)

圖3 體積壓縮率變化曲線Fig.3 Curve of volume compressibility
1.2 管坯材料性能參數
管坯采用0Cr18Ni9Ti板材卷焊管(初始壁厚t0=0.5 mm)。在工藝理論分析中忽略管材卷曲和焊接對管坯材料性能的影響,用原始板材的單向拉伸性能試驗測定其材料參數。從板材上截取試件長度方向與板材軋制方向分別成0°、45°和90°的試件,測試得到流動應力曲線(圖4),塑性變形階段可用線性方程精確擬合:
(6)
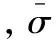

圖4 0Cr18Ni9Ti板材流動應力曲線Fig.4 Flow stresscurves of 0Cr18Ni9Ti sheet
擬合方程參數見表3。
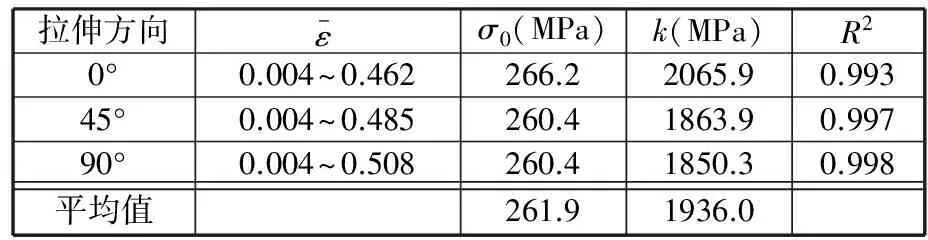
表3 0Cr18Ni9Ti板材材料性能參數表
2 脹形工藝理論分析
在顆粒介質內壓和摩擦的共同作用下,自由脹形區管材環向伸長向外擴張,根據變形特征建立ORZ坐標系,如圖5所示,并給定管件成形過程力學模型基本假設條件:
(1)自由脹形區管壁外輪廓為圓弧;
(2)管材塑性變形處于平面應力狀態,即厚向應力σt=0;
(3)忽略管材彈性變形,材料符合剛塑性硬化特征;
(4)管材符合各向同性特征,塑性變形服從Mises屈服準則。
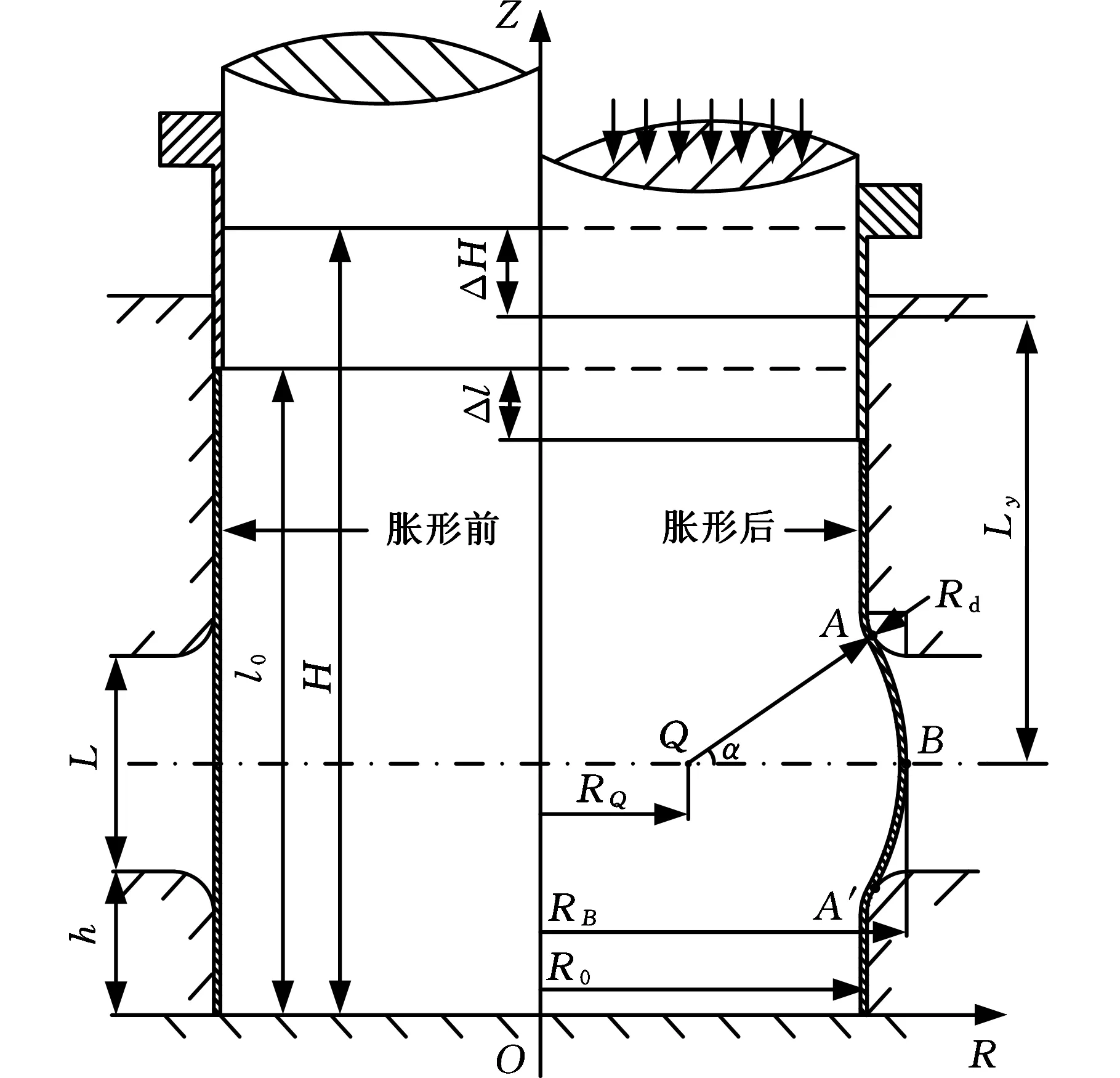
圖5 自由脹形幾何模型Fig.5 Geometric model of free bulging
2.1 幾何模型
圖5顯示管件外輪廓圓弧的圓心為Q點,半徑為Rf(mm),且外輪廓與垂直于Z軸的平面相交為一系列的整圓。圖5中B(RB,ZB)點為脹形區頂點,A(RA,ZA)和A′(RA′,ZA′)點分別為脹形區外輪廓與凹模圓角的相切點,α為貼模角(rad)。H和ΔH分別為顆粒高度和壓頭下壓量(mm)。在ORZ坐標系中,整個管坯的外輪廓形狀可用下面的函數表示:
(7)
式中,h、Rd和L為模具幾何參數,mm;h為下模高度;Rd為凹模圓角;L為脹形區長度;R0、l0和Δl為管坯幾何參數,mm;R0為管坯原始半徑;l0為初始長度;Δl為管端收縮量。
由幾何關系可得以下方程:
R0+Rd(1-cosα)=RQ+Rfcosα
(8)
(9)
RB=Rf+RQ
(10)
將式(8)、式(9)和式(10)聯立可得
(11)
(12)
(13)
因此,A(RA,ZA)和A′(RA′,ZA′)點的坐標可由以下關系式確定:
RA=RA′=RQ+Rfcosα
(14)
(15)
(16)
根據變形前后管坯體積不變可得
(17)
式中,δ為自由脹形區和圓角貼模處管壁體積求解時所選取的積分變量;t為管坯變形瞬時壁厚,mm。
脹形前后t的變化很小,用t0代替對積分結果的影響較小,于是式(17)可轉化為
L-2Rd
(18)
成形前后,顆粒介質承載產生的體積減縮,引入體積壓縮率可得
(19)
由式(19)可推導壓頭的下壓量表達式:
(20)
其中,體積壓縮率η是與壓頭力相關的函數,滿足式(5);被積函數R2的表達式可根據式(7)求解。
根據上述計算過程,在已知模具參數、管坯初始參數和顆粒介質裝料高度的情況下,除了壓頭下壓量ΔH外,所有幾何參量均可表示為RB的函數表達式。
2.2 力學模型
管坯脹形過程中,顆粒介質的內壓和外摩擦力是促使材料發生變形的主要因素。內壓垂直作用于管壁,且沿Z軸的數值分布規律符合傳壓試驗所得到的結果;外摩擦力符合庫侖摩擦定律。根據試驗結果,可將內壓分布規律p(Z)轉化為頂點B內壓pB的函數。
頂點B距壓頭的距離Ly=H-ΔH-h-L/2,代入式(3)可得
(21)
式(21)變形可得壓頭力的計算公式:
(22)
管坯上任取一點(R,Z)距壓頭的距離為H-ΔH-Z, 代入式(3)可得
p(Z)=0.3386pNe-0.014 56(H-ΔH-Z)
(23)
將式(22)代入式(23)可將內壓分布規律p(Z)轉化為頂點B內壓pB的函數:
(24)
將式(24)代入式(4)可得顆粒介質與管材摩擦因數的表達式:
(25)
2.2.1 自由脹形區應力應變分析
管材脹形的任一時刻,在自由脹形區任取一點C(R,Z),分析變形前后該點單元體和單元體所在圓環體的體積變化(圖6)。
變形前單元體和圓環體的體積分別為
dV0=R0t0dZ0dθ0
(26)
V0=2πR0t0dZ0
(27)

圖6 自由脹形區應力應變分析Fig.6 Stress and strain analysis for free bulging region
式中,dθ0、dZ0分別為變形前單元體的環向角度(rad)和軸向長度(mm)。
變形后單元體和圓環體的體積分別為
dV=ρθtRfdτdθ
(28)
V=2πRRftdZ
(29)
式中,ρθ為C點環向曲率半徑,mm;R為C點R軸坐標值,mm;dθ、dτ分別為變形后單元體的環向角度和切向角度,rad。
由幾何關系知:
(30)
式中,β為線段QC與線段QB的夾角(圖6)。
根據體積不變條件dV0=dV和V0=V,可得
(31)
定義dl=Rfdτ,代入式(29)可得
(32)
根據式(32)可以得到自由脹形區任一點C的環向應變εθ和厚向應變εt:
εθ=ln(R/R0)
(33)
εt=ln(t/t0)
(34)
同時,根據體積不變條件可計算切向應變εZ:
εZ=-εθ-εt
(35)
單元體的受力狀態如圖6所示。由單元體的法向平衡可得
(36)
式中,σθ、σZ分別為環向和切向應力,MPa;p為介質內壓,MPa;Sθ、SZ分別為單元體環向和切向切面的面積,mm2;S為單元體內表面面積,mm2;Fθ為環向摩擦力fθ沿法向的投影,N。
由幾何關系知:
(37)
Fθ可用下面的積分式進行計算:
(38)
其中,ψ為積分變量(圖6)。
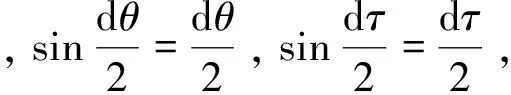
(39)
2.2.2 管坯平衡分析
線段QC繞Z軸旋轉一周將管坯剖分,建立管坯受力分析模型,如圖7所示,由管坯沿Z軸方向的平衡可知
f1+2πRtσZcosβ=f2+F
(40)
式中,f1為介質與管坯之間的摩擦力沿Z軸的分量,N;f2為模具與管坯之間的摩擦力沿Z軸的分量,N;F為介質內壓沿Z軸的分量,N。
f1、f2、F分別用下面的積分進行計算:
(41)
(42)
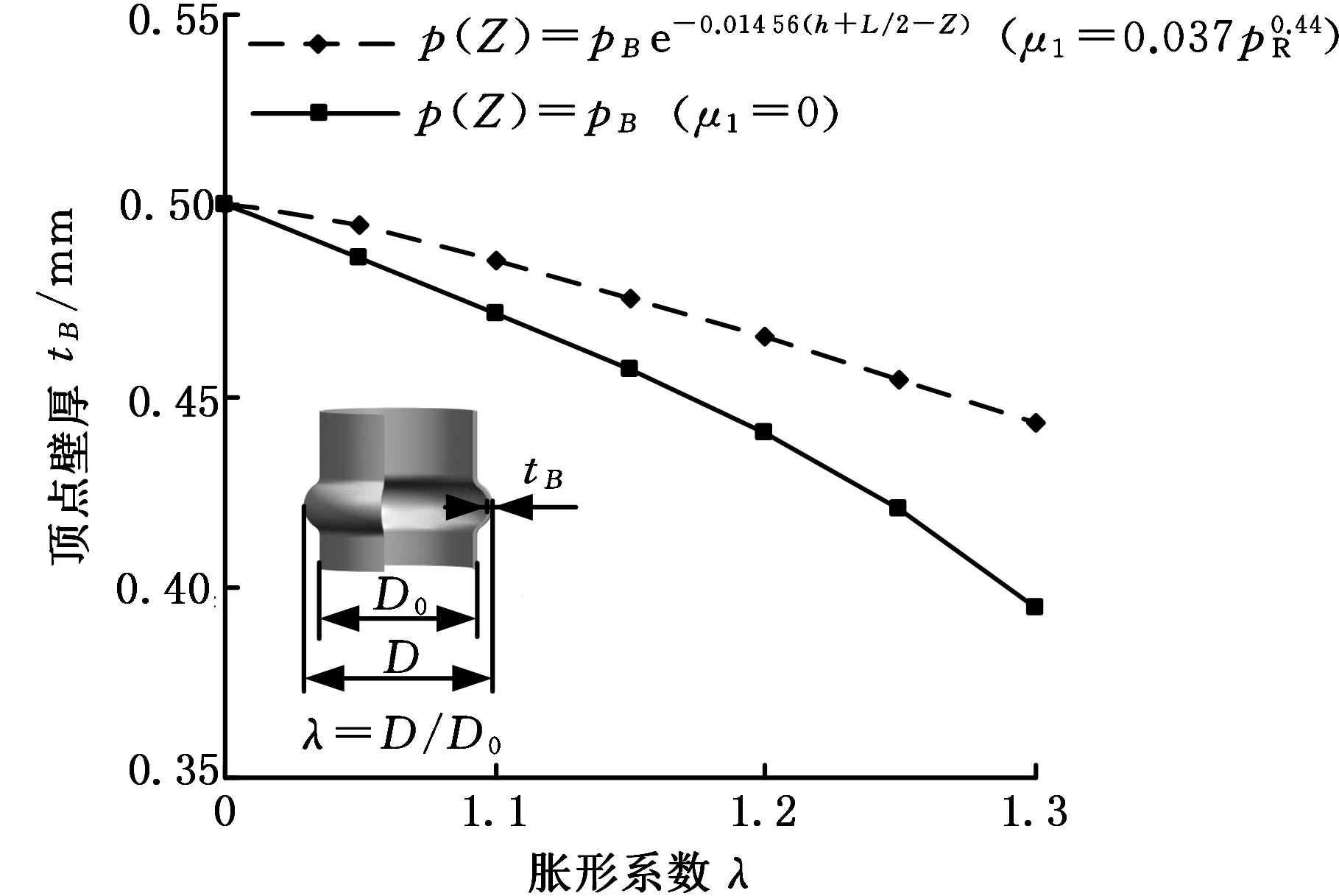
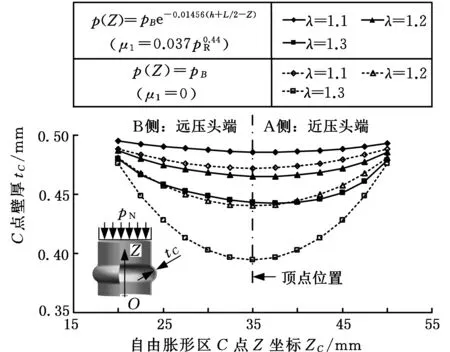
當C點在頂點上方,即h+L/2≤ZC (43) 當C點在頂點下方,即ZA′ (44) 在式(41)~式(44)中,γ和φ分別為計算過程中在自由脹形區和圓角貼模區所選取的積分變量(圖7);R1和R2分別為相應積分限區間所對應的輪廓形狀函數;內壓p的表達式由式(24)確定。 圖7 管坯受力平衡分析Fig.7 Force equilibrium analysis for tube 由圖7中的幾何關系可知 cosγ=(R1-RQ)/Rf (45) (dR)2+(dZ)2=(Rfdγ)2 (46) tanγ=dR/dZ (47) 由式(46)和式(47)可得 dγ=dZ/(cosγRf) (48) 同理: cosφ=(R0+Rd-R2)/Rd (49) dφ=dZ/(cosγRd) (50) 由外輪廓形狀函數式(7)可知 (51) (52) 應用上述幾何條件,可將式(41)~式(44)的積分式轉換為被積函數只含有變量Z且積分變量為Z的定積分。 應用式(40)和式(39)即可推導得到脹形區任一點的切向應力和環向應力表達式: (53) (54) 其中,由式(30)可推導: cosβ=(R-RQ)/Rf (55) ρθ=Rf+RQ/cosβ (56) 由外輪廓形狀函數式(7)可推導: (57) 將幾何模型中幾何參量的計算結果代入力學模型的計算過程,則對于任一給定的脹形直徑(RB已知),只要已知脹形區任一點的Z坐標,則該點的主應力分量可通過式(53)和式(54)計算,主應變分量可通過式(33)、式(34)和式(35)計算。由于計算過程所涉及積分式中的積分函數形式復雜、沒有原函數,故主應力分量的計算結果得不到函數解析式。整理變量可知最終的計算結果中只含有該點內壓p和壁厚t兩個未知量,下文將采用數值法處理計算過程。 2.3 求解過程 將上述過程得到的應力應變代入本構方程,通過求解本構方程便可得到未知參數。 (58) (59) 平面應力狀態下,由伊留辛全量理論可得各應力分量和應變分量之間的關系[15]: (60) 由2.2.2的分析結果可知,應力應變的計算結果中只含有p和t兩個未知量,所以,將等效應力應變代入式(6),將各應力應變分量代入式(60),可得到一個關于p和t的方程組,即 (61) 解此方程組,便可求得未知參量p和t。 脹形過程中,自由脹形區頂點的變形最大,此點需先滿足塑性條件,變形才能繼續進行;因此,頂點的解析是整個求解過程的關鍵。 將頂點的Z坐標h+L/2代入式(61),可解得頂點的內壓pB和壁厚tB。將求得的pB代入內壓分布規律表達式式(24)可得到整個管壁上的內壓分布。此時,對于脹形區任一點,內壓pC為已知量,將該點的Z坐標ZC代入式(61)中的任意一個方程,解此方程可得到該點的壁厚tC。將求得的pB和壓頭下壓量表達式式(20)代入式(22)可得到一個關于壓頭力pN的方程: h(pN)=0 (62) 解此方程可求得壓頭力。 整個求解過程中,代數運算、積分計算和方程(組)求解都通過MATLAB編程實現,且采用數值解法處理積分運算和方程(組)求解過程。程序流程如圖8所示。 圖8 工藝解析過程流程圖Fig.8 Flow diagram of process analysis 2.4 結果與討論 為分析兩個特點對壁厚分布和成形壓力的影響,令傳壓性能參數b=0、顆粒與管材的摩擦因數μ1=0,可得到均布內壓無介質摩擦條件下的解析結果,并與顆粒介質脹形工藝解析結果進行對比,如圖9所示。算例的模具參數為:h=15 mm,L=30 mm,Rd=6 mm。管坯參數為:R0=50 mm,t0=0.5 mm,l0=90 mm。管坯與模具之間的摩擦因數取μ2=0.08,顆粒介質裝料高度H=110 mm。 圖9a給出了理論求解得到的脹形區頂點壁厚在成形過程中的變化情況。由圖9a可知,隨著脹形的發展,由顆粒介質脹形工藝得到的頂點壁厚解析結果與內壓均布且無內摩擦條件(液壓脹形特征)下的結果均呈現近似線性遞減。但是,具有液壓脹形特征的頂點壁厚減薄明顯大于顆粒介質脹形工藝的頂點壁厚減薄。由此可見,顆粒介質脹形工藝的兩大特征可有效減小脹形過程中頂點的壁厚減薄。 (a)脹形區頂點壁厚變化 (b)脹形區壁厚分布 1.p(Z)=pB,μ1=0時的成形內壓2.顆粒介質脹形管坯最大內壓 3.顆粒介質脹形脹形區頂點內壓(c)內壓變化曲線 (d)不同壓力指數下的脹形區壁厚分布圖9 不同內壓狀況、摩擦條件下的理論計算結果對比Fig.9 Calculated results under different pressure and friction conditions 圖9b給出了不同脹形程度下脹形區壁厚分布規律。由圖9b可知,顆粒介質脹形工藝得到的壁厚分布明顯大于內壓均布且無內摩擦條件下的壁厚分布,且越靠近脹形區頂點位置壁厚差別越大。此外,內壓均布且無內摩擦條件下的壁厚分布是關于頂點位置對稱的(圖中虛線),而顆粒介質脹形工藝得到的壁厚分布不關于頂點位置對稱(圖中實線),且近壓頭端壁厚略小于遠壓頭端。由此可見,顆粒介質脹形工藝的兩大特征可有效減小脹形過程中整個脹形區的壁厚減薄,且造成脹形區壁厚非對稱分布,近壓頭端壁厚略小于遠壓頭端壁厚。隨著脹形的發展,兩大特征對壁厚減薄的降低作用越來越明顯,當脹形系數達到1.3時,最大壁厚減薄率相差9.62%。 圖9c給出了成形過程中壓力的變化情況。顆粒介質脹形過程中,管壁所受的介質徑向壓力沿遠離壓頭方向遞減分布,因此管壁所受最大內壓在A側(近壓頭端)管端處。內壓均布且無內摩擦條件下管壁所受內壓處處相等,均等于脹形區頂點內壓。由圖9c可知,顆粒介質脹形工藝中,無論是頂點內壓(曲線3)還是管坯所受最大內壓(曲線2)均小于內壓均布且無內摩擦條件下的成形內壓(曲線1),且隨著脹形的發展壓力值差別越來越大。由此可見,顆粒介質脹形工藝的兩大特征可有效減小脹形過程中所需的成形壓力,當脹形系數達到1.3時,顆粒介質脹形管坯所受最大內壓僅為內壓均布且無內摩擦條件下成形內壓的41.2%。 力學模型中,內壓分布函數是根據固定壁面條件下的顆粒介質傳壓性能試驗建立起來的。然而,在管坯成形過程中,脹形區為浮動壁面,這必將會改變顆粒介質壓力傳遞的衰減狀況。壓力傳遞衰減狀況的變化將會對脹形區壁厚分布帶來怎樣的影響,本文計算了不同壓力指數條件下的壁厚分布情況來說明此問題(圖9d)。由圖9d可知,不同壓力指數條件下脹形區壁厚分布的計算偏差非常小,當壓力指數在試驗值附近變化不超過一倍時,壁厚計算偏差在初始壁厚的1%以內。因此,通過顆粒介質傳壓性能所建立起來的內壓分布函數在工程誤差允許的范圍內可以應用于管坯內高壓成形工藝。 根據工藝原理設計試驗模具,在通用壓力設備上進行管件脹形試驗。壓力設備和試驗模具如圖10所示。試驗用管坯采用0Cr18Ni9Ti板材卷焊而成(D0=100 mm,t0=0.5 mm)。試驗用顆粒采用8號NMG,該顆粒在高壓下具有很好的流動性。試驗得到了不同脹形程度的自由脹形管件(圖10),測量不同管件的壁厚變化情況,分別與理論計算結果進行對比(圖11)。試驗中,壓頭力可通過壓力設備讀數除以壓頭面積得到,實測壓頭力與理論計算結果的對比如圖11所示。 (a)試驗設備 (b)試驗模具 (c)不同脹形程度管件 (d)不同脹形區高度剖切管件圖10 工藝試驗設備、模具、產品圖Fig.10 Experimental facilities, die and products 圖11a給出了三個脹形直徑下自由脹形區理論計算壁厚分布(實線)和試驗結果(虛線)的對比曲線。由圖可知,理論計算結果與試驗結果基本吻合,當脹形直徑D=110 mm、120 mm和130 mm時,理論計算最大壁厚相對誤差分別為1.96%、1.64%和0.87%。由此可見,隨著脹形的發展,計算誤差有減小的趨勢,這是因為脹形開始階段,脹形區輪廓形狀與理想圓弧差別較大,而隨著脹形的發展脹形區輪廓形狀越來越接近圓弧(圖10c)。 由圖11b可知,壓頭力理論計算結果與試驗結果基本吻合,最大相對誤差為4.5%。由此可見,本文所構建的力學模型可用于管件顆粒介質脹形工藝成形力的預測。 (a)脹形區壁厚分布對比 (b)壓頭力變化對比 (c)管坯外輪廓曲線對比圖11 理論計算與試驗結果對比曲線Fig.11 Correlation curves of calculation and test 圖11c給出了不同脹形區高度條件下脹形區外輪廓形狀的理論假設和試驗測試對比曲線。由圖可知,在遠壓頭管端理論假設的圓弧輪廓模型與試驗結果偏差較大;在近壓頭管端偏差較小;輪廓曲線最大誤差不超過8%。管壁的外輪廓形狀與成形內壓分布互為因果,顆粒介質脹形工藝內壓的非均勻性是造成近壓頭端和遠壓頭端管壁外形呈非對稱形狀的主要原因。 (1)顆粒介質脹形工藝所具有的內壓非均勻分布、介質與管坯摩擦作用顯著的兩大特征可有效抑制管件脹形區壁厚減薄。當脹形系數達到1.3時,顆粒介質脹形的最大壁厚減薄率低于內壓均布且無內摩擦條件9.62%。 (2)顆粒介質脹形工藝可有效減小成形壓力,且隨脹形發展效果增強,當脹形系數達到1.3時,顆粒介質脹形管坯所需內壓僅為內壓均布且無內摩擦條件的41.2%。 (3)顆粒介質傳壓性能試驗的邊界條件雖與工藝試驗有所不同,但是通過傳壓試驗建立起來的內壓函數模型在工程誤差允許的范圍內可應用于工藝試驗,理論分析得到的管件壁厚分布和成形力與工藝試驗基本吻合,最大誤差不超過1.96%和4.5%。本文所建立的力學模型和求解方法可用于管件脹形的預測和分析。 (4)顆粒介質內壓的非均勻性會帶來管壁外形的非對稱性,本文理論模型所作的管壁外輪廓為圓弧的假設具有一定的局限性(適用于脹形區高度與初始管坯直徑比值小于0.35的情況),管壁外形與內壓分布的因果關系有待進一步研究。 [1] BOUDEAU N, MALéCOT P.A Simplified Analytical Model for Post-processing Experimental Results from Tube Bulging Test: Theory, Experimentations, Simulations[J]. International Journal of Mechanical Sciences,2012,65(65):1-11. [2] HE Zhubin, YUAN Shijian, LIN Yanli, et al. Analytical Model for Tube Hydro-bulging Test, Part I: Models for Stress Components and Bulging Zone Profile[J]. International Journal of Mechanical Sciences,2014,87(4):297-306. [3] HE Zhubin, YUAN Shijian, LIN Yanli, et al. Analytical Model for Tube Hydro-bulging Tests, Part Ⅱ: Linear Model for Pole Thickness and Its Application[J]. International Journal of Mechanical Sciences,2014,87(4):307-315. [4] HWANG Y M, WANG C W.Flow Stress Evaluation of Zinc Copper and Carbon Steel Tubes by Hydraulic Bulge Tests Considering Their Anisotropy[J]. Journal of Materials Processing Technology,2009,209(9):4423-4428. [5] 趙長財, 任學平, 董國疆, 等. 管材固體顆粒介質成形工藝及其塑性理論研究[J]. 中國機械工程,2007,18(16):2000-2005. ZHAO Changcai, REN Xueping, DONG Guojiang, et al. Process of Solid Granule Medium Forming and Plastic Research[J]. China Mechanical Engineering,2007,18(16):2000-2005 [6] 董國疆, 趙長財, 曹秒艷, 等. 圓筒件固體顆粒介質成形壁厚及變形規律研究[J]. 中國機械工程,2010,21(16):1992-1998. DONG Guojiang, ZHAO Changcai, CAO Miaoyan, et al. Study on Wall-thickness and Deformation Regularity of Cylinder Part Based on Solid Granule Medium Forming[J]. China Mechanical Engineering,2010,21(16):1992-1998. [7] DONG Guojiang, ZHAO Changcai, CAO Miaoyan. Flexible-die Forming Process with Solid Granule Medium on Sheet Metal[J]. Transactions of Nonferrous Metals Society of China (English Edition),2013,23(9):2666-2677. [8] CAO Miaoyan, ZHAO Changcai, WU Lijun, et al. Lubricant Research on SGMF of Magnesium Alloy Sheet[J]. Advanced Materials Research,2013,675:311-316. [9] DONG Guojiang, ZHAO Changcai, YA Yuanyu-an, et al. Discrete Element and Finite Element Coupling Simulation and Experiment of Hot Granule Medium Pressure Forming[J]. Transactions of Nonferrous Metals Society of China (English Edition),2015,28(3):580-591. [10] 郎利輝, 劉康寧, 吳為, 等. TA1鈦合金板材高溫顆粒介質成形試驗研究[J]. 航空制造技術,2015(17):122-123. LANG Lihui, LIU Kangning, WU Wei, et al. Experimental Research on Hot Granular Medium Forming of TA1 Titanium Alloy Sheet[J]. Aeronautical Manufacturing Technology,2015(17):122-123. [11] 陳國亮. 顆粒介質成形工藝研究[D]. 南京: 南京航空航天大學,2008. CHEN Guoliang. Research on Drawing Technology With Solid Granules[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2008. [12] 袁海環. 固體顆粒介質板料拉深成形工藝研究[D]. 沈陽: 沈陽航空工業學院,2010. YUAN Haihuan. Reach on Sheet Metal Deep Drawing Process with Solid Granule Medium[D]. Shenyang: Shenyang Aerospace University,2010. [13] GRüNER M, MERKLEIN M.Numerical Simulation of Hydro Forming at Elevated Temperatures with Granular Material Used as Medium Compared to the Real Part Geometry[J]. International Journal of Material Forming,2010,3(1):279-282. [14] GRüNER M, MERKLEIN M.Consideration of Elastic Tool Deformation in Numerical Simulation of Hydroforming with Granular Material Used as a Medium[J]. Key Engineering Materials,2011,473:707-714. [15] 俞漢清, 陳金德. 金屬塑性成形原理[M]. 北京:機械工業出版社,1998:121-127. YU Hanqing, CHEN Jinde. Fundamental of Metal Plastic Forming[M]. Beijing: Mechanical Industry Press,1998:121-127. (編輯 袁興玲) Theoretical Analyses of Tube Granule Medium Internal High Pressure Forming Processes YANG Zhuoyun1ZHAO Changcai1DONG Guojiang2ZHANG Xin1CHEN Xiaohua1 1.Key Laboratory of Advanced Forging & Stamping Technology and Science of Ministry of Education of China(Yanshan University),Qinhuangdao,Hebei,066004 2.College of Vehicles and Energy,Yanshan University,Qinhuangdao,Hebei,066004 The discrete granules brough a non-uniform internal pressures and a significant friction between tube and medium to granule medium internal high pressure forming processes. Therefore, a non-uniform pressure transfer model was built for this process to investigate into theoretical analyses of tube bulging. The effects of the non-uniform pressures and the significant friction on tube forming property were studied by the theoretical analyses which were verified by processing tests. The analyses show that the non-uniform pressures and the significant friction may reduce the thickness reductions and forming pressures of tube bulging. The comparison of theoretical analyses and processing tests indicates that the calculated curves of thickness distributions and forming pressures agree well with test results. The non-uniform pressure transfer model for granule medium internal high pressure forming process may be used for the predictions and analyses of tube forming processes. granule medium; internal high pressure forming; tube; bulging 2016-05-24 國家自然科學基金資助項目(51305386,51305385);河北省自然科學基金資助項目(E2013203093) TG301 10.3969/j.issn.1004-132X.2017.07.018 楊卓云,男,1990年生。燕山大學機械工程學院博士研究生。主要研究方向為管板材特種成形技術。E-mail: zhuoyun1990@163.com。趙長財,男,1964年生。燕山大學機械工程學院教授、博士研究生導師。董國疆,男,1978年生。燕山大學車輛與能源學院副教授。張 鑫,男,1992年生。燕山大學機械工程學院碩士研究生。陳曉華,男,1988年生。燕山大學機械工程學院博士研究生。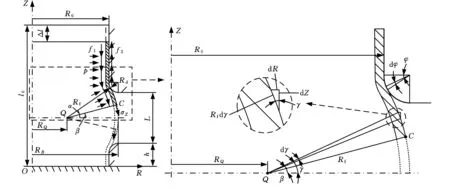
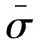


3 工藝試驗





4 結論

