巧用變式 領(lǐng)悟規(guī)律
——含有兩個變量的函數(shù)的任意性和存在性問題
張曉藝●
巧用變式 領(lǐng)悟規(guī)律
——含有兩個變量的函數(shù)的任意性和存在性問題
河南省信陽高級中學(xué)高三文科(1)班(464000)
張曉藝●
在各種資料,在考試甚至高考中,經(jīng)常出現(xiàn)兩個變量的函數(shù)問題,這類問題課本上并沒有出現(xiàn)過,但它的知識源于課本中涉及到的兩集合間的關(guān)系,及函數(shù)最值,既能考查學(xué)生基礎(chǔ)知識的掌握又能考查學(xué)生分析問題解決問題的能力,源于課本,高于課本,故這類問題備受命題者青睞.以前筆者在學(xué)習(xí)中是用遇到一個,記錄一個的方法處理的,當(dāng)時也能搞明白,但過后再考,仍然做不對,出錯率極高,在最近我市的一次考試中,又設(shè)計了這樣一道選擇題,題目如下:
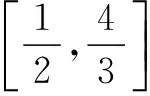
考后通過閱卷分析發(fā)現(xiàn),即使是很優(yōu)秀的學(xué)生,這道題也出錯,問卷調(diào)查后發(fā)現(xiàn)錯因有兩個:
(1)不會分析問題,無法把該問題轉(zhuǎn)化為兩段函數(shù)值域之間的關(guān)系,反映出能力不足;
(2)即使分析出要求兩段函數(shù)值域,但求解f(x)的值域時出錯,反映出基礎(chǔ)不牢.針對這種情況同學(xué)們是這樣處理的:
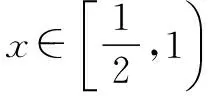
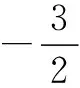
但我的探索卻沒有停止,為了認(rèn)清這類問題的本質(zhì),學(xué)會分析,在此題的基礎(chǔ)上又設(shè)計了以下三道變式:
在上面例1的基礎(chǔ)上,我和同學(xué)們對上述變式展開討論,得出的結(jié)論如下:
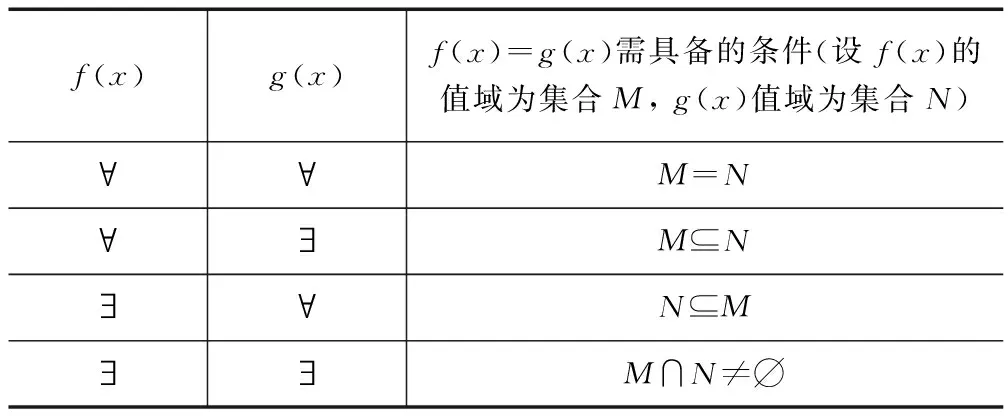
f(x)g(x)f(x)=g(x)需具備的條件(設(shè)f(x)的值域為集合M,g(x)值域為集合N)??M=N??M?N??N?M??M∩N≠?
下面對例1再做一組變式,以便更深刻地理解這類問題.
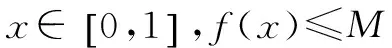
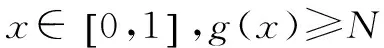
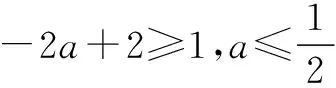
在借鑒變式四的分析思路的基礎(chǔ)上,學(xué)生類比概括出以下規(guī)律:

f(x)g(x)f(x)≤g(x)需具備的條件??f(x)max≤g(x)min??f(x)max≤g(x)max??f(x)min≤g(x)min??f(x)min≤g(x)max
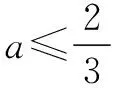
通過以上8個問題的專題講解,學(xué)生對含有兩個變量的函數(shù)的任意性,存在性問題的求解思路清晰明了,在后來各類考試中再出現(xiàn)這類問題都能準(zhǔn)確求解.
下面提供兩道綜合題,再次體會上述規(guī)律的應(yīng)用.
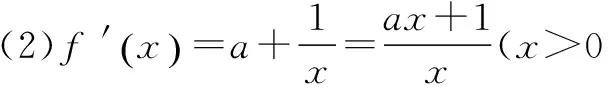
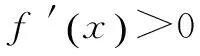
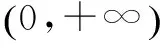
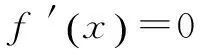
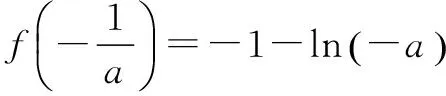
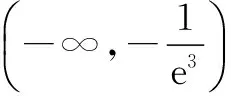
G632
B
1008-0333(2017)01-0050-02

