單相級聯H橋整流電路非線性控制策略

孫玉巍 劉教民 李永剛 付 超 楊喆明

(新能源電力系統國家重點實驗室(華北電力大學) 保定 071003)

?

單相級聯H橋整流電路非線性控制策略

孫玉巍 劉教民 李永剛 付 超 楊喆明

(新能源電力系統國家重點實驗室(華北電力大學) 保定 071003)

針對電力電子牽引變壓器輸入級單相級聯H橋(CHB)整流電路的非線性及擾動工況，提出一種基于靜止坐標系的非線性優化控制策略。根據系統仿射非線性模型及微分幾何理論，提出基于部分反饋線性化的零動態設計方案，對其線性部分采用二次型最優方法以確定反饋增益，并引入諧振環節以實現零相差跟蹤；對于零動態則采用基于擴張狀態觀測器的自抗擾控制策略，以提高系統在負載大范圍擾動時的控制品質。實驗結果表明，該控制策略能提高CHB系統在電網電壓及負載擾動時的動態響應速度，保證網側電流及直流電壓快速穩定調節，同時使網側在單位功率因數下運行，各模塊直流電壓均衡。

單相級聯H橋 靜止坐標 狀態反饋 零動態 自抗擾控制

0 引言

基于電力電子及中高頻大功率變壓器技術的電力電子牽引變壓器(Power Electronic Traction Transformer，PETT)能夠實現輕量化、高功率密度、低諧波及能量交互，已成為國內外研究的熱點[1-3]，而作為其輸入級的單相級聯H橋(Cascade H-Bridge，CHB)整流器則是PETT能夠實現上述目標的關鍵。一方面，為獲得“凈化”的電力電子接口，需要對并網電流進行精確控制，實現網側低諧波、單位功率因數運行；另一方面，由于PETT運行工況復雜，電網電壓和負載擾動劇烈，要求系統具有較強的抗擾能力。

針對單相或三相PWM整流電路的非線性、強耦合，基于微分幾何的非線性控制方法近年來受到了廣泛關注[4-7]。通過適當的非線性狀態反饋和坐標變換，可將非線性系統精確或部分線性化，從而采用線性系統的優化控制方法。文獻[4]通過引入關系度為2的能量函數作為系統輸出，實現了PWM整流器精確線性化，但將能量函數作為單一控制目標的方法僅適用于dq坐標系下有功電流指令為直流量的情況。文獻[5，6]針對三相PWM整流電路，采用將并網電流精確線性化，而將直流電壓作為零動態通過外環予以控制的方法，并在電壓環分別引入變速積分及非線性抗擾積分以提高系統抗擾能力，這兩種方法均借鑒了自抗擾控制(Active Disturbance Rejection Control，ADRC)非線性光滑反饋的優點，但沒有涉及作為ADRC核心的擴張狀態觀測器(Extended State Observer，ESO)。ESO可實時估計系統狀態及總和擾動信息，并用給予補償的方法取代誤差積分反饋作用[8，9]，對非線性、擾動劇烈的PETT應用場合具有較好的應用前景。此外，上述非線性控制方案均基于dq旋轉坐標系，當用于單相CHB整流器時，還需構建正交虛擬電路以實現dq變換[10]，而本文CHB作為PETT輸入級，只需要實現網側單位功率因數運行，無需提供無功補償功能，因此可采用簡單的基于靜止坐標系的控制方法。

為實現并網電流對電網電壓的零相位差跟蹤及對特定諧波的抑制，目前基于靜止坐標系的PWM整流控制方法多為基于內模原理的重復控制[11，12]、比例諧振(PR)控制[13，14]。PR控制器的比例系數kp和諧振系數kr的整定，均依賴于系統近似線性化模型，當用于PETT大范圍負載擾動工況時，其控制品質將難以保證；且kp、kr共同影響系統響應，當采用根軌跡法整定時，需要多族根軌跡進行分析，以實現兩參數的相互配合取值，整定較困難[15]。

本文針對PETT輸入級CHB電路靜止坐標系模型提出基于部分反饋線性化的零動態控制策略。根據微分幾何非線性理論，對系統狀態反饋線性化過程進行詳細推導，由此選擇以并網電流為可控量，直流電壓的二次方為零動態的設計方案。對于線性部分采用二次型最優方法確定反饋增益，并引入諧振環節以補償系統相差；對零動態采用基于ESO的ADRC控制，以提高系統在負載大范圍擾動時的控制品質。最后將所提控制策略應用于采用混合PWM(Hybrid PWM，HPWM)調制的5模塊CHB系統，通過實驗對其控制品質進行了驗證。

1 系統建模及其狀態反饋非線性控制

1.1 級聯H橋整流器仿射非線性模型

級聯式PETT拓撲如圖1所示，由輸入級CHB及后級隔離雙向DC-DC變換器(Isolated Bidirectional DC-DC Converter，IBDC)構成，本文研究對象為前級CHB整流器，而將后級IBDC用等效負載電阻RL表示，vs和is分別為電網電壓、電網電流，Ls為交流濾波電感，Rs為其等效電阻，van為CHB總的交流輸出電壓，vhi、vdci(i=1，2，…，N)分別為第i個模塊的交流端電壓及直流電壓，C為直流電容，S1～S4為電力電子開關器件，各模塊參數均相同。

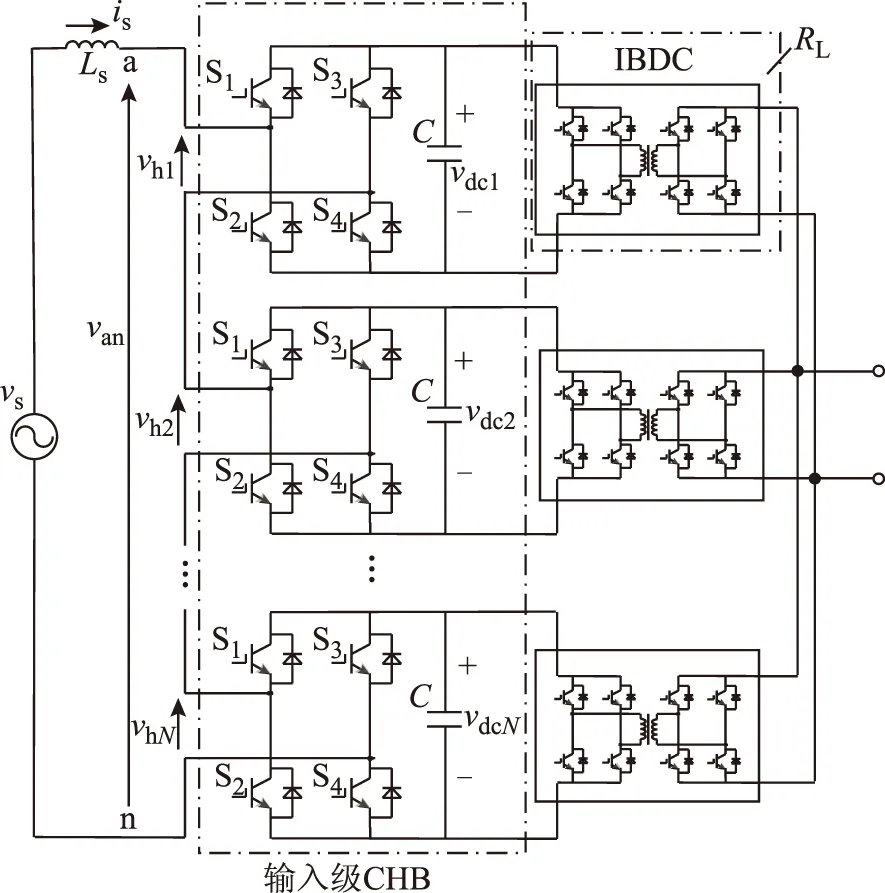
圖1 級聯式PETT主電路拓撲Fig.1 Main circuit topology of cascaded PETT

根據基爾霍夫定律，可列寫CHB狀態方程為

(1)

式中，hi為各H橋開關函數，i=1，…，N。當S1、S4導通時，hi=1；當S2、S3導通時，hi=-1；當S1、S3或S2、S4導通時，hi=0。

假設各直流電壓均衡，即vdc1=vdc2=…=vdcN=vdc，vdc為各模塊直流電壓平均值，則系統狀態方程為

(2)

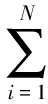
(3)

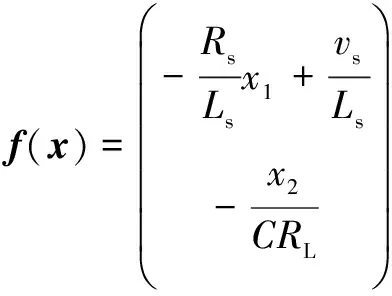
觀察狀態方程可知其對狀態變量呈非線性，對控制變量呈線性，為仿射非線性系統。系統輸出方程根據實際控制目標，可有多種選擇，輸出方程不同。決定系統的關系度不同。若關系度等于系統階數，則可以采用狀態反饋精確線性化設計方法；如果關系度小于系統階數，則可采用部分反饋線性化零動態設計方法[16]。

1.2 狀態反饋非線性控制原理

1)狀態反饋精確線性化條件。

根據微分幾何非線性控制理論[16，17]，式(3)所示仿射非線性系統可以實現狀態反饋精確線性化，當且僅當存在一個區域Ω使得下列條件成立：

以上條件若滿足，就必然存在一個輸出函數ω(x)，使得在Ω上系統的關系度等于系統階數n，該系統可以被完全精確線性化為可控的線性系統。

已知式(3)所示系統n=2，對其求Lie括號，有

(4)

(5)

可知矩陣[g，adfg]秩為2，條件(1)滿足。又由于集合{g}是對合的，條件(2)也滿足。因此可以找到一個函數ω(x)，使其滿足條件Lgω(x)=0，LgLfω(x)≠0，即系統關系度為2，等于系統階數。

(6)

經驗證：LgLfω(x)≠0，符合條件。

可見只有將輸出函數選為關系度為2的能量函數時，式(3)才能實現精確線性化。而對于實際單相CHB系統，并網電流需要精確跟蹤正弦指令，直流電壓指令為直流量，如將能量函數作為直接控制對象，控制器設計困難，因此更適合選用以并網電流為輸出函數的零動態設計方案。

2)零動態標準型。

選擇并網電流與其參考值之差作為輸出函數

y=h(x)=x1-iref

(7)

由Lgh(x)=-vdc/Ls≠0可知系統關系度為r=1，小于系統階數2，又由系統滿足條件(1)和條件(2)，根據非線性控制零動態設計原理，存在函數η(x)滿足條件Lgη(x)=0，使得系統在坐標變換z=Φ(x)=[h(x)η(x)]T下，可轉換為零動態標準型

(8)

式中，第一式為線性系統動態方程；第二式為零動態方程。根據實際系統可直接選擇η(x)為零動態變量，也可以選擇η(x)中的不可控部分為零動態變量，由式(6)可直接選取

(9)

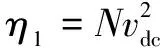
(10)

由式(10)可看出，零動態的特征根s=-2/(CRL)位于左半復平面，因此零動態漸近穩定。但若零動態不加控制，當負載電阻RL較大時，特征根離虛軸很近，直流電壓的過渡時間將很長。為改善零動態在負載大范圍擾動時的動態性能，本文采用基于ADRC的零動態控制策略，在第2.2節闡述。

2 CHB控制系統設計

2.1 基于狀態反饋二次型最優及諧振補償的并網電流控制策略

將式(8)第一式寫成線性系統形式為

(11)

式中，A=0；B=1。選取二次型性能指標為

(12)

式(12)中第一項體現了控制過程中和終端時刻的狀態誤差趨近于0，第二項是對控制幅度的限制。因狀態變量及預控變量為一維，權矩陣Q和R均為一個正數，設使性能指標為最小的最優控制為

v*=-K*z1

(13)

則反饋增益系數為K*=R-1BTP，P是Riccati矩陣方程PA+ATP-PBR-1BTP+Q=0的正定對稱解。

對權矩陣Q的確定，取式(9)能量函數第一項構造性能指標，即

(14)

可得Q=Ls/2，并且選擇權矩陣R=Ls2/f，f為系統等效開關頻率。

將A、B、Q、R代入Riccati方程，可解得矩陣P和反饋增益K*，將求得的反饋增益代入式(13)、式(11)，即可得到原非線性系統的反饋控制律u為

(15)

式中，iref為并網電流指令，iref=Irefsin(ωt)，sin(ωt)為與電網電壓同相位的正弦信號，Iref為并網電流幅值指令。

由式(15)所得并網電流非線性控制框圖如圖2a所示。由于輸入iref為正弦變化量，若僅采用單增益狀態反饋會產生跟蹤相位差。對此，根據內模及重復控制原理[18]，本文在狀態反饋環中引入諧振控制器Gr(s)，如圖2b所示。諧振控制器傳遞函數為

(16)

式中，ωc為考慮實際系統實現及電網允許頻率波動引入的帶寬量，若電網頻率允許波動范圍為±0.8 Hz，ωc=1.6π=5 rad/s[15]。對于k′，根據以其為參量的單條根軌跡即可容易整定。

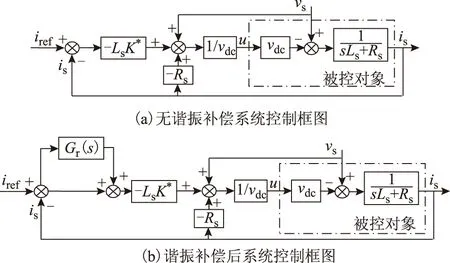
圖2 并網電流非線性控制閉環框圖Fig.2 The nonlinear closed loop control diagram of grid current

根據閉環特征方程相同的原則，由圖2b可得以k′為開環增益的等效開環傳遞函數為

(17)

設系統參數Ls=8 mH，Rs=0.2 Ω，等效開關頻率f=2 kHz，由Matlab lqr指令可計算反饋增益K*=790，代入式(17)，繪出以k′為參變量的系統根軌跡如圖3所示，s1、s2、s3為特征根，選擇阻尼比最大的極點(黑色方框中)，對應增益k′的值為40。

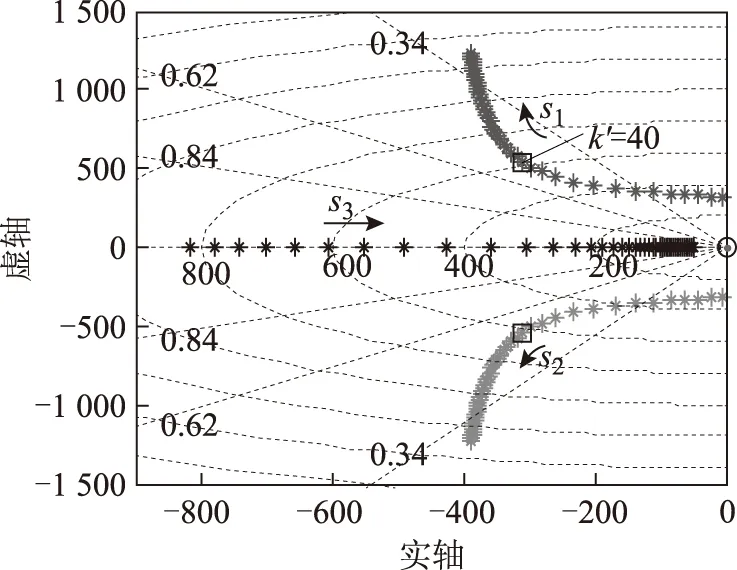
圖3 以k′為參變量的系統根軌跡Fig.3 Root locus of the system depending on parameter k′

2.2 基于ADRC的零動態控制

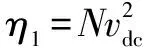
將式(10)中網側瞬時功率vsiref用有功功率vmIref/2代替，vm為電網電壓幅值，零動態方程可寫為

(18)

式中，u′為并網電流幅值指令，u′=Iref；f為由系統內部不確定性及外部擾動共同作用的總擾動項[8]，采用二階非線性ESO進行估計，表達式為

(19)

式中，γ1為η1的觀測值；γ2為對總擾動項f的估計值；β1、β2為觀測器增益；采用非線性函數fal(e，α，δ)可避免高頻振顫現象的出現，其中α為非線性因子，δ為濾波因子。fal(e，α，δ)函數表達式為

(20)

在ESO對系統狀態及總擾動能獲得較好估計的基礎上，令

(21)

則零動態方程可轉換為典型一階線性系統

=kp(η1ref-η1)

(22)

式中，kp為系統帶寬，kp越大，調節時間ts越短，考慮PWM控制、采樣延遲而留取一定裕量，本文取kp≈5/ts，若需ts為0.1 s時，kp為50。

對于ESO非線性函數參數α、δ，根據文獻[8]對fal(e，α，δ)的大量測試，要求0<α<1，其值越小非線性越強，本文取α1=0.25，α2=0.5，濾波因子δ=0.01。對于ESO反饋增益β1和β2，采用線性極點配置方法，忽略式(19)中非線性函數，令β1=2ω0，β2=ω02[19]，ω0為二階線性ESO帶寬，要求其必須大于反饋控制器帶寬kp，考慮采樣速率及噪聲容限，本文選ω0=4kp。

根據圖2及2.2節對CHB整流器非線性電流環及自抗擾零動態控制器的設計，可得CHB整體控制策略如圖4所示，圖中PLL表示鎖相環，CHB采用HPWM調制技術，具體見第4節。

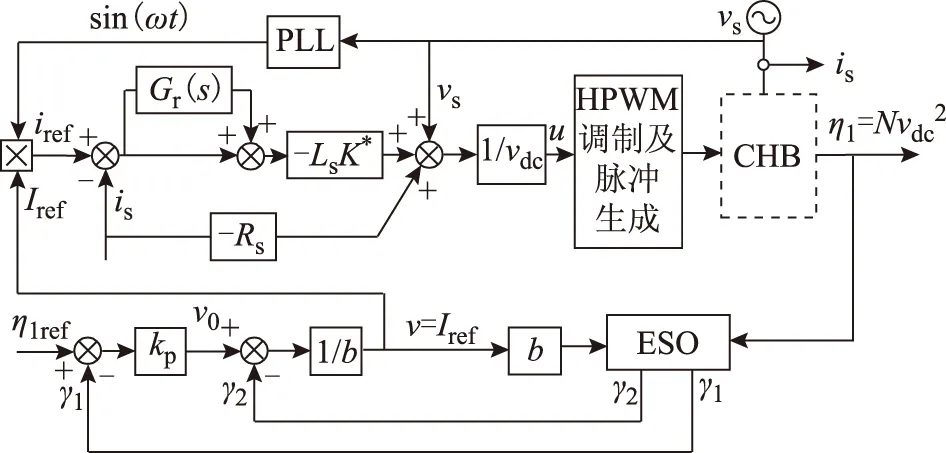
圖4 CHB整流器整體控制策略Fig.4 Overall control strategy of the CHB rectifier

3 HPWM調制策略

在上述控制策略生成總占空比調制信號u的基礎上，為降低系統開關頻率，采用階梯波與PWM相結合的HPWM調制方法[20]，基本原理如圖5所示。利用N-1個模塊工作于階梯波模式，1個模塊工作于PWM模式，兩者輸出波形疊加，即可得到2N+1電平PWM電壓波形，該方法可降低系統整體開關頻率，且保證波形質量。

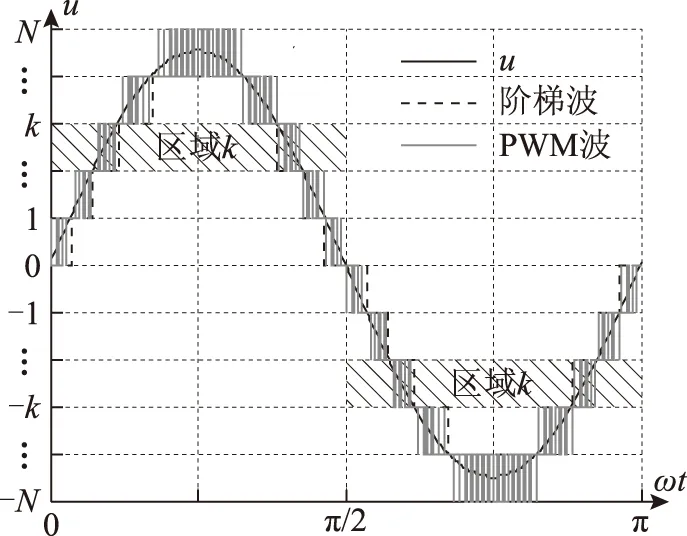
圖5 HPWM調制原理Fig.5 Principle of HPWM modulating strategy

HPWM調制實現方法可描述為：

首先將總調制信號u進行取整運算以得到當前多電平電壓區域k為

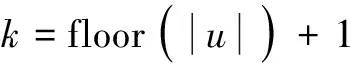
(23)

式中，floor(·)為向低取整的函數，k=1,2,…,N。

然后將各模塊直流電壓進行排序，并根據當前k值、調制信號u及并網電流is極性，確定各模塊開關函數hi，以保證直流電壓均衡。基于電壓排序的HPWM算法實施流程如圖6所示，可描述為：

1)當u>0，is>0，令直流電壓較低的k-1個模塊工作于+1開關模式，第k個模塊工作于PWM模式，其余工作在0模式。

2)當u>0，is<0，令直流電壓較高的k-1個模

塊工作于+1開關模式，第k個模塊工作于PWM模式，其余工作于0模式。

3)當u<0，is>0，令直流電壓較高的k-1個模塊工作于-1開關模式，第k個模塊工作于PWM模式，其余工作于0模式。

4)當u<0，is<0，令直流電壓較低的k-1個模塊工作于-1開關模式，第k個模塊工作于PWM模式，其余工作于0模式。

工作于PWM模式的H橋調制波ut為

ut=u-(k-1)sign(u)

(24)

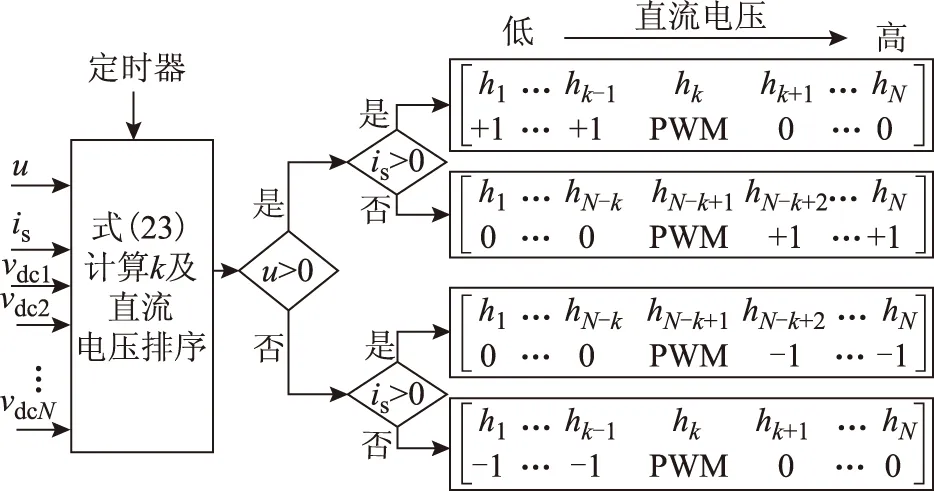
圖6 HPWM調制算法流程Fig.6 Flowchart of the HPWM algorithm

4 實驗驗證

搭建小功率5模塊級聯CHB實驗平臺，如圖7所示，其中HB1～HB5為5個H橋模塊，控制器采用DSP+FPGA架構，DSP28335主要實現控制算法，FPGA采用XilinxXC3S400芯片，主要負責采樣、通信和PWM脈沖生成。

實驗參數：電網電壓vs頻率為50 Hz，其有效值由160 V階躍至200 V，濾波電感Ls=8 mH，內阻Rs=0.2 Ω，直流側電容C=20 mF，vdcref=60 V，負載擾動時，模塊等效負載電阻由50 Ω切換為25 Ω；HPWM調制載波頻率fc=2 kHz。

圖7 5模塊CHB整流器實驗平臺Fig.7 Laboratory setup of the five-module CHB rectifier

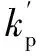
圖8為兩種控制策略電網電壓擾動時網側和直流電壓實驗波形對比，負載不變。圖8a、圖8b為網側波形結果，包括并網電流is、電網電壓vs及多電平交流電壓van；圖8c、圖8d為直流電壓波形對比。由實驗錄波得到相應的對比結果見表1。可知當電網電壓擾動時，兩種控制策略并網電流均可由原穩態值3.3 A過渡至新穩態值2.6 A，在本文控制策略下，并網電流調節時間僅為15 ms(0.75個周波)，而PR-PI控制下約為70 ms(3.5個周波)。對于直流電壓波形，當電網電壓擾動時，本文控制策略下直流電壓幾乎無明顯突變；而PR-PI控制下約有3 V的上升，經約300 ms恢復穩態60 V，表明本文控制策略抗擾能力較強。兩種控制策略下穩態波形相差不大，在200 V額定電網電壓下，多電平輸出電壓van為11電平波形，總諧波畸變率(THD)均約為13.4%，經交流濾波電感濾波后，穩態并網電流波形THD僅為2.7%，且與電網電壓同相位。

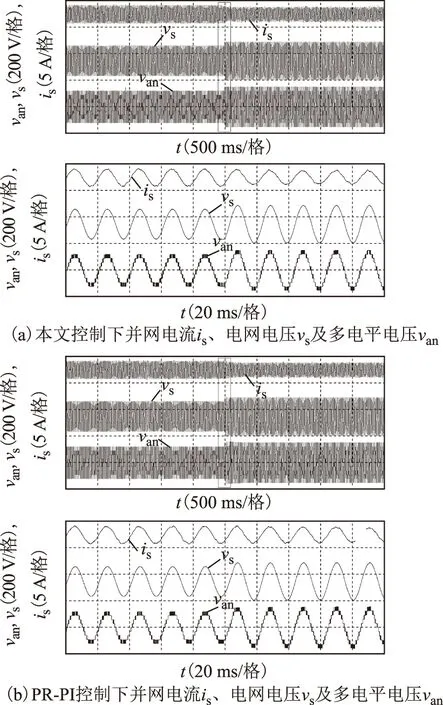
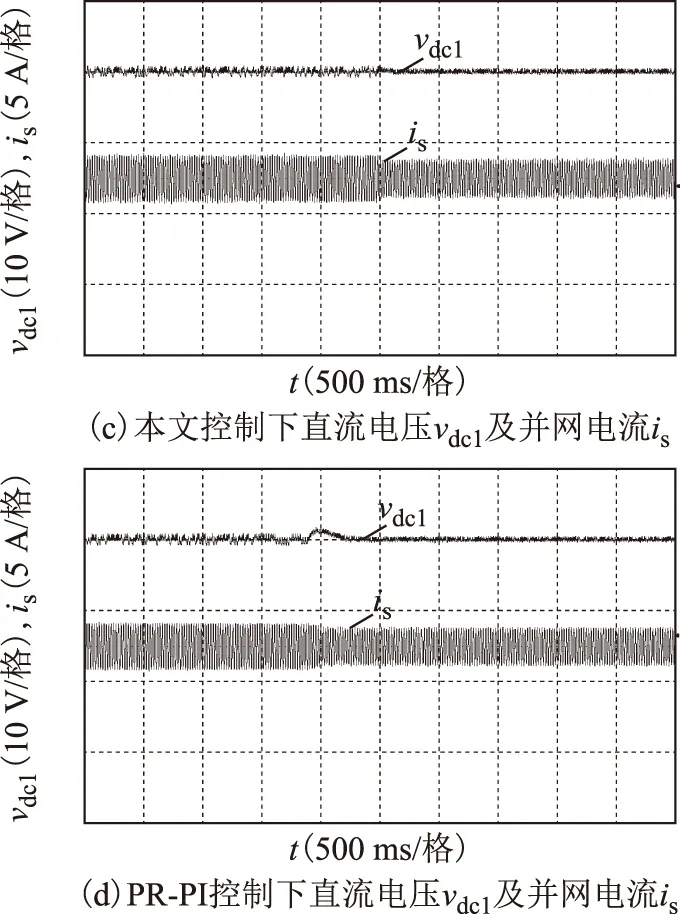
圖8 兩種控制策略下電網電壓擾動實驗結果比較Fig.8 Comparison of experimental results between two control methods under grid voltage disturbed case

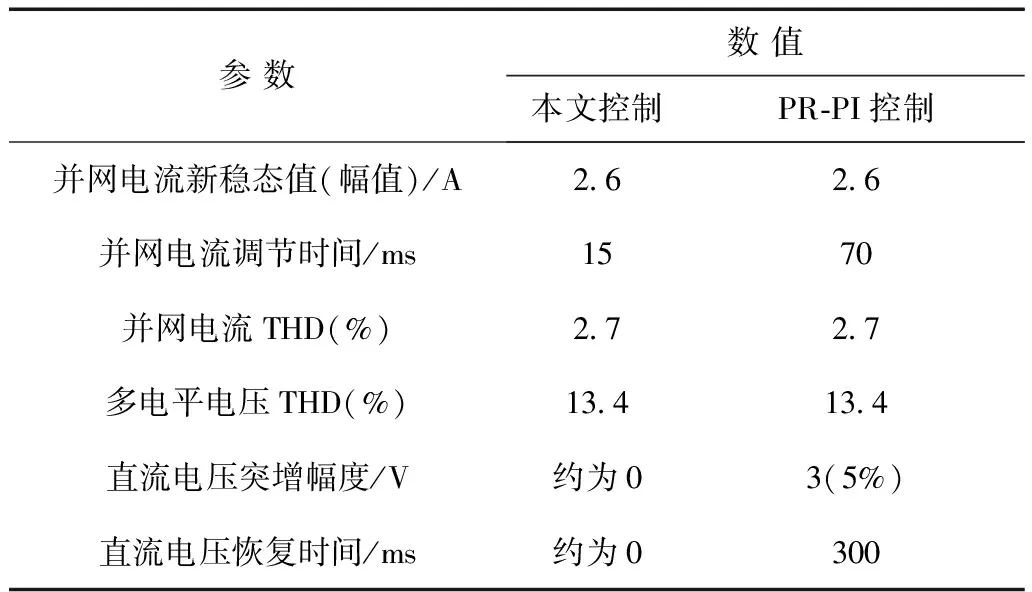
表1 兩種控制策略電網電壓擾動下實驗結果對比

圖9為兩種控制策略在加載擾動時(負載功率由360 W增加至720 W)的實驗對比結果。由實驗錄波得到相應的對比結果見表2，可知當負載擾動時，兩種控制策略下并網電流均可由原穩態值2.6 A過渡至新穩態值5.2 A，但本文控制下并網電流調節時間僅為15 ms(0.75個周波)，而PR-PI控制下調節時間約為40 ms(2個周波)。對于直流電壓波形，當負載增加時，本文控制下直流電壓僅下降2 V，經100 ms即可恢復；而PR-PI控制下直流電壓下降幅度約為5 V，經150 ms恢復。該結果表明所提控制策略對負載擾動具有較好的控制品質。

圖10為本文控制策略下5個模塊直流電壓波形，均穩定在參考值60 V，加載之前電壓紋波約2.5%，負載增加后，導致電容充、放電電流亦增加，因此電壓紋波增加至4%。該結果表明文中基于電壓排序的HPWM調制算法可有效實現直流電壓的均衡。

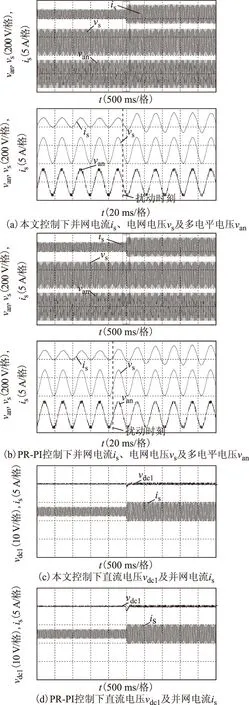
圖9 兩種控制算法下負載擾動時實驗結果比較Fig.9 Comparison of experimental results between two control methods under load disturbed case

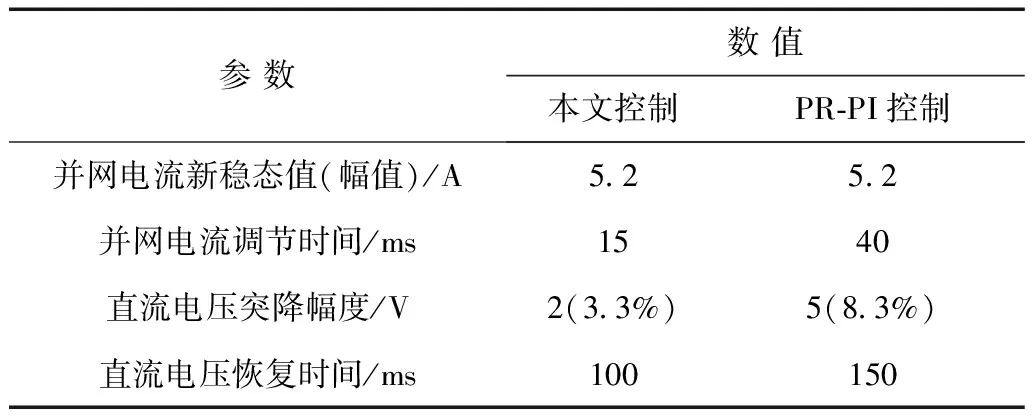
參數數值本文控制PR?PI控制并網電流新穩態值(幅值)/A5 25 2并網電流調節時間/ms1540直流電壓突降幅度/V2(3 3%)5(8 3%)直流電壓恢復時間/ms100150

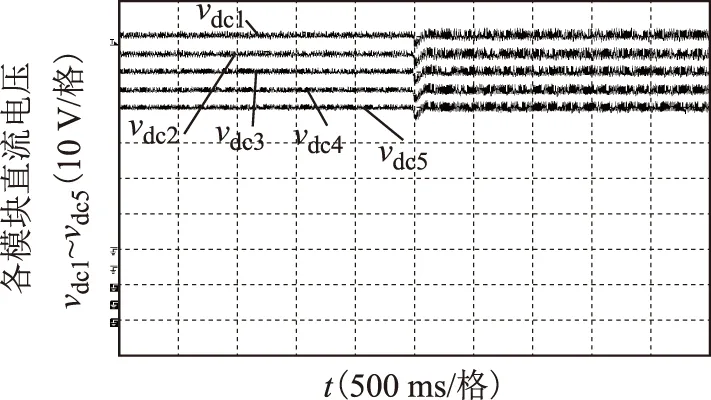
圖10 本文控制算法下5個模塊直流電壓波形Fig.10 Waveforms of dc voltages of the five modules under the proposed control strategy

5 結論

本文對CHB系統基于靜止坐標系的非線性控制策略進行研究，提出以并網電流為可控量、直流電壓平方量為零動態的部分反饋線性化零動態控制方案。

1)對系統線性化部分采用二次型最優方法以確定反饋增益，并在反饋環引入諧振控制以實現電流零相位差跟蹤，由于反饋增益已確定，諧振系數可在系統全局線性化模型的基礎上，通過根軌跡法進行整定，由于參量只有一個，因而整定過程較容易。

2)選擇直流電壓二次方量為零動態，可得到一階零動態方程，進而采用一階ADRC控制器，控制算法易于實現；且可提高系統在負載大范圍擾動時的控制品質，對PETT時變負載場合具有較好的應用價值。

[1] 李偉，張黎.鐵道牽引單相電力電子變壓器及控制[J].鐵道學報，2013，35(4)：37-42. Li Wei，Zhang Li.Railway traction single-phase power electronics transformer and control[J].Journal of the China Railway Society，2013，35(4)：37-42.

[2] Dujic D，Zhao Chuanhong，Mester A，et al.Power electronic traction transformer-low voltage prototype[J].IEEE Transactions on Power Electronics，2013，28(12)：5522-5533.

[3] 律方成，郭云翔，付超，等.基于磁鏈分區的大功率中頻變壓器漏感參數計算方法[J].電工技術學報，2016，31(5)：164-169. Lü Fangcheng，Guo Yunxiang，Fu Chao，et al.Calculation method for leakage inductance of high power medium frequency transformers based on flux linkage partition[J].Transactions of China Electrotechnical Society，2016，31(5)：164-169.

[4] 孟建輝，石新春，付超，等.三相VSG系統的高性能非線性控制策略[J].中國電機工程學報，2014，34(6)：863-871. Meng Jianhui，Shi Xinchun，Fu Chao，et al.A high-performance nonlinear control strategy of three-phase VSG systems[J].Proceedings of the CSEE，2014，34(6)：863-871.

[5] 孟建輝，石新春，王毅，等.VSG系統直流電壓快速穩定的控制策略研究[J].電工技術學報，2014，29(8)：219-226. Meng Jianhui，Shi Xinchun，Wang Yi，et al.Research on a fast and stable DC voltage control strategy of voltage sag generator system[J].Transactions of China Electrotechnical Society，2014，29(8)：219-226.

[6] 張曉華，郭源博，周鑫，等.PWM整流器的欠驅動特性與非線性控制[J].中國電機工程學報，2011，31(33)：85-92. Zhang Xiaohua，Guo Yuanbo，Zhou Xin，et al.Underactuated property and nonlinear control for PWM rectifier[J].Proceedings of the CSEE，2011，31(33)：85-92.

[7] 屈克慶，李文旗，葉天凱，等.基于狀態反饋的LCL型逆變器解耦控制策略[J].電工技術學報，2016，31(20)：130-137. Qu Keqing，Li Wenqi，Ye Tiankai，et al.State feedback based decoupling control strategy for grid-connected inverter with LCL filter[J].Transactions of China Electrotechnical Society，2016，31(20)：130-137.

[8] 韓京清.自抗擾控制技術—估計補償不確定因素的控制技術[M].北京：國防工業出版社，2013.

[9] 劉英培，梁海平，栗然.基于無源性與自抗擾控制的雙饋風力發電系統研究[J].電工技術學報，2015，30(18)：122-130. Liu Yingpei，Liang Haiping，Li Ran.Research on doubly-fed wind power generation with passivity-based control and active disturbance rejection control[J].Transactions of China Electrotechnical Society，2015，30(18)：122-130.

[10]孫毅超，趙劍鋒，季振東，等.一種基于虛擬電路閉環的單相PWM整流器控制新方法[J].電工技術學報，2013，28(12)：222-230. Sun Yichao，Zhao Jianfeng，Ji Zhendong，et al.A novel closed-loop control approach for single-phase PWM rectifier based on virtual circuit[J].Transactions of China Electrotechnical Society，2013，28(12)：222-230.

[11]張學廣，馬彥，李瑞，等.兩相靜止坐標系下并網逆變器的重復控制策略[J].電工技術學報，2016，31(9)：85-91. Zhang Xueguang，Ma Yan，Li Rui，et al.Repetitive control strategy for grid-connected converters in stationary frame[J].Transactions of China Electrotechnical Society，2016，31(9)：85-91.

[12]趙學華，史麗萍，陳麗兵.基于復合控制的改進型級聯STATCOM控制策略[J].電力系統保護與控制，2015，43(17)：98-106. Zhao Xuehua，Shi Liping，Chen Libing.A new current control strategy of cascaded STATCOM with composite control[J].Power System Protection and Control，2015，43(17)：98-106.

[13]郭小強，賈曉瑜，王懷寶，等.三相并網逆變器靜止坐標系零穩態誤差電流控制分析及在線切換控制研究[J].電工技術學報，2015，30(4)：8-14. Guo Xiaoqiang，Jia Xiaoyu，Wang Huaibao，et al.Analysis and online transfer of stationary frame zero steady-state error current control for three-phase grid-connected inverters[J].Transactions of China Electrotechnical Society，2015，30(4)：8-14.

[14]陳素華.基于多載波和PR控制實現變換器并聯環流抑制研究[J].電力系統保護與控制，2016，44(11)：129-134. Chen Suhua.Multicarrier PWM and PR control strategy of circulating current reduction for grid-connected converters[J].Power System Protection and Control，2016，44(11)：129-134.

[15]黃華，周波達，費建平，等.基于根軌跡法的鏈式STATCOM比例諧振電流控制器設計[J].江蘇電機工程，2015，34(2)：1-9. Huang Hua，Zhou Boda，Fei Jianping，et al.Design of current proportional-resonant controller for chained STATCOM basing on root-locus method[J].Jiangsu Electrical Engineering，2015，34(2)：1-9.

[16]Isidori A.非線性控制系統[M].王奔，莊圣賢，譯.北京：電子工業出版社，2005：172-228.

[17]盧強，梅生偉，孫元章.電力系統非線性控制[M].北京：清華大學出版社，2008：56-108.

[18]楊云虎，周克亮，程明，等.單相PWM變換器相位補償諧振控制方案[J].電工技術學報，2013，28(4)：65-71. Yang Yunhu，Zhou Keliang，Cheng Ming，et al.Phase compensation resonant control scheme for single phase PWM converters[J].Transactions of China Electrotechnical Society，2013，28(4)：65-71.

[19]Gao Zhiqiang.Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the American Control Conference，Denver，Colorado，2003：4989-4996.

[20]Iman-Eini H，Schanen，J L，Farhangi S，et al.A modular strategy for control and voltage balancing of cascaded H-bridge rectifiers[J].IEEE Transactions on Power Electronics，2008，23(5)：2428-2442.

(編輯 赫蕾)

Nonlinear Control Strategy of Single-Phase Cascade H-Bridge Rectifier

SunYuweiLiuJiaominLiYonggangFuChaoYangZheming

(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power University Baoding 071003 China)

A static coordinate based nonlinear optimal control strategy was presented for the single-phase cascade H-bridge(CHB)rectifier，serving as the input stage of the power electronic traction transformer，for its nonlinear and disturbed operating conditions.According to the nonlinear affine model of CHB and nonlinear differential geometric theory，the zero-dynamic control scheme based on partial feedback linearization was preferred.For the linear part，the feedback gain was optimized using the linear quadratic control method，and a resonant controller was added for achieving zero phase error tracking.For the zero-dynamic variable，the active disturbance rejection controller(ADRC)based on extended state observer was designed to improve its dynamic response under wide range of load disturbance.Experimental results show that the proposed control strategy has good performance in improving dynamic response under grid voltage and load disturbances，guaranteeing fast regulation and stability of grid current and dc voltage，meanwhile achieving unity power factor operation and dc voltage balance of each module.

Single-phase cascade H-bridge(CHB)，static coordinate，state feedback，zero-dynamic，active disturbance rejection controller(ADRC)

國家科技支撐計劃(2013BAG24B02)和中央高校基本科研業務費專項資金(2015XS112)資助項目。

2016-08-20 改稿日期2016-12-21

TM464

孫玉巍 女，1987年生，博士研究生，研究方向為電力電子技術在電力系統中的應用和電力電子變壓器。

E-mail：sunyuwei@ncepu.edu.cn(通信作者)

劉教民 男，1958年生，教授，博士生導師，研究方向為新能源電力系統特性與多源互補等。

E-mail：ljm6667@126.com